Euler's fundamental discoveries about the exponential function: Their role in quantum computing
Marek Gluza
NTU Singapore
Click links at slides.com/marekgluza
Outline:
- Infinite sums
- Euler's formula
- Infinite products
Read Euler - he is the master of us all.
- Pierre-Simon Laplace
Sums and infinite sums
S_2 = 1 + 1/2 = 1.5
S_3 = 1 + 1/2 + 1/4 = 1.75
S_4 = 1 + 1/2 + 1/4 +1/8 = 1.875
In times of Euler, mathematics was an experimental science:
What will be the value of \(S_\infty\)?
S_\infty = 1 + 1/2 + 1/4 +1/8 + \ldots
Will it exceed \(S_\infty>2\)?
Sums and infinite sums
Let us use a trick:
Euler (and later Ramanujan) was famous for playing with infinite sums. This trick works but Euler made mistakes too. Generations of mathematicians after him had to provide a proof that his intuition was correct.
S_\infty = 1 + 1/2\times (1+1/2 + 1/4 + \ldots )
S_\infty = 1 + 1/2 \times S _\infty
1/2 \times S_\infty = 1
S_\infty = 2
Sums and infinite sums
S_\infty = 1 + 1/2+ 1/4 + \ldots \\
S_\infty(q) = \lim_{N\rightarrow\infty}\sum_{n=0}^N q^n = \lim_{N\rightarrow \infty} \frac{1-q^{N+1}}{1-q}
S_\infty(q) = \sum_{n=0}^\infty q^n = \frac{1}{1-q} \quad\text{if}\quad |q|< 1
Check: \(S_\infty(q=1/2) = 1 / (1-1/2) =2\)
The exponential function
\quad\text{where}\quad n! = 1\cdot 2\cdot 3\cdot\ldots \cdot n
e^x = \sum_{n=0}^\infty \frac{1}{n!} x^n
x\in\mathbb R
Above, \(|q|<1\) was a restriction. Here \(1/n!\) coefficients remove the restriction and \(x\in \mathbb R\) can be arbitrary.
S_\infty(q) = \sum_{n=0}^\infty q^n = \frac{1}{1-q} \quad\text{if}\quad |q|< 1
We understood \(q\in \mathbb C\). What if \(q\) was a matrix?
Check: It makes sense to ask this because if \(A\in \mathbb C ^{d\times d} \) then \(A^k\in \mathbb C ^{d\times d} \) and we can add matrices of the same dimension.
S_\infty(A) = \sum_{n=0}^\infty A^n = \frac{I}{I-A} \quad\text{if}\quad \max_{i,j}|A_{i,j}|< 1/d
Quantum mechanics
used to be called matrix mechanics
Matrix inversion?!
Quantum mechanics
is all about exponentials
If \(A\in \mathbb C ^{n\times n} \) then we can define the exponential:
e^A = \sum_{n=0}^\infty \frac{1}{n!} A^n
It means: multiply the matrix with itself \(n\) times and sum it up with the coefficient \(1/n!\)
I cannot draw a picture of \(e^A\) like for \(e^x\). But I will show you why choosing \(A\) to be \(A = \begin{pmatrix} 0 &1\\-1 & 0\end{pmatrix}\) is useful in quantum computing.
\sum_{n=0}^\infty A^n = \frac{I}{I-A}
\text{if}\quad \max_{i,j}|A_{i,j}|< 1/d
It means: multiply the matrix with itself \(n\) times and sum it up with the coefficient \(1/n!\) (this was missing before).
Outline:
- Infinite sums
- Euler's formula
- Infinite products
Euler was studying complex numbers:
\(z = x+iy\) where \(x,y\in \mathbb R\) and \(i^2 = -1\)
He asked: What would be the exponential of a purely complex number \(e^{z} = e^{iy}\)?
e^z = \sum_{n=0}^\infty \frac{1}{n!} z^n
= 1 + i y + \frac 12 i^2 y^2 + \frac 1 6i^3 y^3 + \ldots
= 1 + i y -\frac 12 y^2 - \frac 1 6i y^3 + \ldots
Euler wrote 800 manuscripts in his life, they included many formulas.
But what he found here is usually called the Euler's formula.
Euler was studying complex numbers:
\(z = x+iy\) where \(x,y\in \mathbb R\) and \(i^2 = -1\)
He asked: What would be the exponential of a purely complex number \(e^{z} = e^{iy}\)?
\sin(x) = \sum_{n=0}^\infty (-1)^n \frac{x^{2n+1} }{(2n+1)! } = x-\frac 16x^3+ \ldots
\cos(x) = \sum_{n=0}^\infty (-1)^n \frac{x^{2n} }{(2n)! } = 1-\frac 12 x^2+ \ldots
e^z = \sum_{n=0}^\infty \frac{1}{n!} z^n
= 1 + i y + \frac 12 i^2 y^2 + \frac 1 6i^3 y^3 + \ldots
= 1 + i y -\frac 12 y^2 - \frac 1 6i y^3 + \ldots
e^{iy} =\cos(y) + i \sin(y)
Braket notation
\mathcal V = \mathbb C^2 = \mathrm{span}_{\mathbb C}\{ e_1, e_2\}
| 0 \rangle :=e_1, | 1\rangle :=e_2
\vec v \in \mathcal V \leftrightarrow |v\rangle = v_0 | 0 \rangle + v_1 | 1\rangle
U \vec v \leftrightarrow U|\psi\rangle
"ket"
"quantum superposition"
In quantum computing, the state of a single qubit is a 2-dimensional vector \(\ket\psi = a \ket{0} +b\ket{1}\).
An operation with duration \(t\) and generated by \(Y=Y^\dagger \in\mathbb{C}^{2\times 2}\) is given by
Quantum computing operation a qubit is given by multiplying a 2-dimensional matrix to that vector.
U = e^{it Y} = \sum_{n=0}^\infty \frac 1{n!} (it)^n Y^n
"quantum evolution"
How can we create \( \frac1 {\sqrt 2} \ket{0} +\frac 1 {\sqrt 2}\ket{1}\)?
e^{i t Y }= \sum_{n=0}^\infty \frac{1}{n!} (i t)^n Y^n
= I + it Y + \frac 12 i^2 t^2 Y^2 + \frac 1 6i^3 t^3 Y^3 + \ldots
= I + i tY-\frac 12 t^2 Y^2 - \frac 1 6i t^3 Y^3 + \ldots
It has the properties
\(Y^2 = I\) and \(Y\ket 0 = - i \ket 1\)
Let us study the matrix \(Y = \begin{pmatrix} 0 &-i\\i & 0\end{pmatrix}\)
It can be engineered by applying oscillatory electromagnetic fields to the qubit.
= I + i tY-\frac 12 t^2 I - \frac 1 6i t^3 Y + \ldots
e^{itY} =\cos(t)I + i \sin(t) Y
e^{itY} \ket 0 =\cos(t)\ket 0 + i \sin(t) Y\ket 0 = \cos(t)\ket 0 + i \sin(t)(-i)\ket 1
This is how we can 'program' the state of the qubit!
e^{it Y} \ket 0 =\cos(t) \ket 0 + \sin(t) \ket 1
Using Euler's formula to 'program a qubit
Outline:
- Infinite sums
- Euler's formula
- Infinite products
Definition of the Euler number:
e =\lim_{N\rightarrow \infty} \left (1+\frac{1} N \right)^N
e^x = \lim_{N\rightarrow \infty} \left (1+\frac{x} N \right)^N
Example:
\(x = 2, N = 100 \)
e^2\approx \left (1+\frac{2} {100} \right)^{100}
e^2\approx 1.02 \times 1.02 \times \ldots 1.02
To think that you multiply the number \(1.02\) with itself \(100\) times and you will get an approximation of \(e^2 \approx 7.39\) - that's what people admire about Euler's formulas!
Infinite products
Definition of the Euler number:
e =\lim_{N\rightarrow \infty} \left (1+\frac{1} N \right)^N
e^x = \lim_{N\rightarrow \infty} \left (1+\frac{x} N \right)^N
e^{it Y} \ket 0 =\cos(t) \ket 0 + \sin(t) \ket 1
We saw that EM drive creates qubit oscillation:
What if we would remove the imaginary number \(i\)?
e^{t Y} \ket 0 =?
It is very difficult to implement it on a quantum computer but if we would find a way then we could make a lot of money solving problems in industry.
\lim_{t\rightarrow \infty} e^{t Y} \approx (I+tY /N)^N
The right-hand side is a polynomial and the protocol called quantum signal processing can be used to implement it on a quantum computer.
Ongoing research on quantum algorithms!
Definition of the Euler number:
e =\lim_{N\rightarrow \infty} \left (1+\frac{1} N \right)^N
e^x = \lim_{N\rightarrow \infty} \left (1+\frac{x} N \right)^N
e^{it Y} \ket 0 =\cos(t) \ket 0 + \sin(t) \ket 1
We saw that EM drive creates qubit oscillation:
What if we would remove the imaginary number i?
e^{t Y} \ket 0 =?
\lim_{t\rightarrow \infty} e^{t Y} \approx (1+tY /N)^N
The right-hand side is a polynomial and the protocol called quantum signal processing can be used to implement it on a quantum computer.
Ongoing research on quantum algorithms!
I'm not sure if Euler had ideas about quantum computations.
I am sure that if he was alive today then he would be working on quantum computing!
It is very difficult to implement it on a quantum computer but if we would find a way then we could make a lot of money solving problems in industry.
Double-bracket quantum algorithms for diagonalization
Marek Gluza
NTU Singapore
slides.com/marekgluza
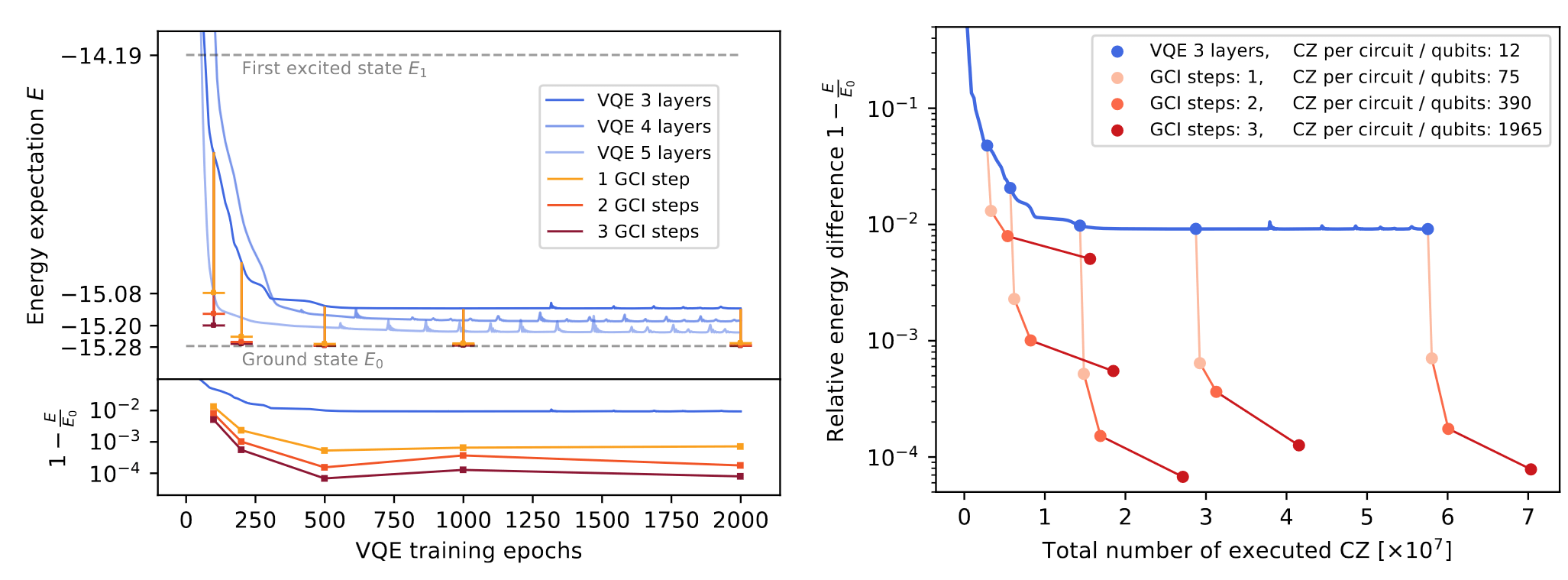
Gate count after VQE warm-start:
C(z,z',t) \approx \frac{\langle \Delta\hat\varphi(z,t)\Delta\hat\varphi(z',t)\rangle}{ \Delta z^2 }
Experimental Observation of Curved Light-Cones in a Quantum Field Simulator
M. Tajik, J. Schmiedmayer
Breaking of Huygens-Fresnel principle in inhomogeneous Tomonaga-Luttinger liquids
Spyros Sotiriadis
Per Moosavi
\partial_{t}^{2} \hat{\phi}
= 2 v(x) v'(x) \partial_{x} \hat{\phi}
+ v(x)^2 \partial^2_{x} \hat{\phi}
\partial_{t}^{2} \hat{\phi}
= v(x)v'(x) \partial_{x} \hat{\phi}
+ v(x)^2\partial^2_{x} \hat{\phi}
\mapsto
Tomography for phonons
\hat H_\text{TLL} = \int \text{d}z\left[ \frac{\hbar^2n_{GP}}{2m}\partial_z\hat\varphi^2+g\delta\hat\varrho^2\right]
\hat H_\text{TLL} = \sum_{k>0} \frac {\hbar \omega_k}2 (\phi_k^2+\delta\hat\rho_k^2) + g\rho_0^2
\langle\hat \phi_k^2(t)\rangle= \cos^2(\omega_k t) \langle \phi_k^2(0)\rangle \\
\quad\quad\quad\quad\quad+\sin^2(\omega_k t) \langle \delta\hat \rho_k^2(0)\rangle
\delta \hat\rho
\langle\hat \phi^2(t)\rangle
\langle\delta\hat \rho^2(0)\rangle =0?
\langle \hat \phi^2(0)\rangle
\hat \phi
https://arxiv.org/abs/1807.04567
https://arxiv.org/abs/2005.09000
Quantum mechanics
used to be called matrix mechanics
S_\infty(q) = \sum_{n=0}^\infty q^k = \frac{1}{1-q} \quad\text{if}\quad |q|< 1
We understood \(q\in \mathbb C\). What if \(q\) was a matrix?
Check: It makes because if \(A\in \mathbb C ^{n\times n} \) then \(A^k\in \mathbb C ^{n\times n} \) and we can add matrices of the same dimension.
S_\infty(A) = \sum_{n=0}^\infty A^k = \frac{1}{1-A} \quad\text{if}\quad \max_{i,j}|A_{i,j}|< 1
Examples of infinite sums
e^x = \sum_{n=0}^\infty \frac{1}{n!} x^k \quad\text{where}\quad n! = 1\cdot 2\cdot 3\cdot\ldots \cdot n
\sin(x) = \sum_{n=0}^\infty (-1)^k \frac{x^{2k+1} }{(2k+1)! } = x-\frac 13 x^3+ \ldots
\cos(x) = \sum_{n=0}^\infty (-1)^k \frac{x^{2k} }{(2k)! } = 1-\frac 12 x^2+ \ldots
Quantum mechanics
used to be called matrix mechanics
exp(A) = \sum_{n=0}^\infty \frac{1}{k!} A^k \quad\text{if}\quad \|A\| < ...?
\| \sum_{n=0}^N \frac{1}{k!} A^k \| \le \sum_{n=0}^N \frac{1}{k!} \|A^k \| \le exp(\|A\|)
\|exp(A)\| = \lim_{N\rightarrow \infty}\| \sum_{n=0}^N \frac{1}{k!} A^k \| \le exp(\|A\|)
\|A\| \ge 0
\|A+B\|\le \|A\| +\|B\|
\|\alpha A\|= |\alpha|\cdot \|A\|
\|A^k\|= \|A\|^k
Quantum mechanics
used to be called matrix mechanics
exp(A) = \sum_{n=0}^\infty \frac{1}{k!} A^k \quad\text{if}\quad \|A\| < ...?
S_\infty(A) = \sum_{n=0}^\infty A^k = \frac{1}{1-A} \quad\text{if}\quad \|A\|< 1
\| \sum_{n=0}^N \frac{1}{k!} A^k \| \le \sum_{n=0}^N \frac{1}{k!} \|A^k \| \le exp(\|A\|)
Why double a bracket?
\partial_t \hat A(t) = i [ \hat A(t), \hat H(t)]
\partial_t \hat A(t) = [ \hat A(t), [\hat A(t), \hat H(t)]]
Why double a bracket?
\partial_t \hat A(t) = i [ \hat H(t), \hat A(t)]
\partial_t \hat A(t) = [ \hat H(t), [\hat H(t), \hat A(t)]]
=
2 qubit unitary
Canonical
\partial_t \hat A(t) = [ \hat A(t), [\hat A(t), \hat H(t)]]
Double-bracket quantum algorithms
are inspired by double-bracket flows
and allow for quantum compiling of short-depth circuits which approximate grounds states
Inspired by double-bracket flows we compiled quantum circuits which yield quantum states relevant for material science
\partial_t \hat A(t) = [ \hat A(t), [\hat A(t), \hat H(t)]]
=
2 qubit unitary
Canonical
\hat H_1 = e^{s_0 \hat W_0} \hat H_0 e^{-s_0 \hat W_0}
\hat W_0
= [\hat D_0,\hat H_0]
Double-bracket rotation ansatz
antihermitian
\left(i\hat H\right)^\dagger = -i \hat H
Rotation generator:
Input:
Unitary rotation:
e^{s \hat W_0}
\hat H_0
Double-bracket rotation:
\partial_s \hat H_0(s) = [\hat W_0, \hat H_0]
\Leftrightarrow
\partial_s \hat H_0(s) = [\hat H_0(s),[ \hat H_0(0),\hat D_0] ]
\partial_t \hat A(t) = [ \hat A(t), [\hat A(t), \hat H(t)]]
\hat H_1 = e^{s_0 \hat W_0} \hat H_0 e^{-s_0 \hat W_0}
\hat W_0
= [\hat D_0,\hat H_0]
Double-bracket rotation ansatz
Rotation generator:
Input:
Unitary rotation:
e^{s \hat W_0}
\hat H_0
Double-bracket rotation:
Key point: If \(\hat D_0\) is diagonal then
\(\hat H_1\) should be "more" diagonal than \(\hat H_0\)
\hat H_0(s) = e^{s \hat W_0} \hat H_0 e^{-s \hat W_0}
\hat W_0
= [\hat D_0,\hat H_0]
Double-bracket rotation ansatz
Rotation generator:
Input:
\hat H_0
Double-bracket rotation:
\sigma(\hat H_0(s))
Restriction to off-diagonal
\partial_s \|\sigma(\hat H_0(s))\|_{\text{HS}}^2 = -2\langle \hat W_0,[\hat H_0, \sigma(\hat H_0)]\rangle_{\text{HS}}
Lemma:
Proof: Taylor expand, shuffle around (fun!)
\hat H(s) = e^{s \hat W_0} \hat H_0 e^{-s \hat W_0}
\hat W_0
= [\hat D_0,\hat H_0]
Double-bracket rotation ansatz
Rotation generator:
Input:
\hat H_0
Double-bracket rotation:
\sigma(\hat H_\ell)
Restriction to off-diagonal
\partial_s \|\sigma(\hat H_0(s))\|_{\text{HS}}^2 = -2\langle \hat W_0,[\hat H_0, \sigma(\hat H_0)]\rangle_{\text{HS}}
Lemma:
Proof: Taylor expand, shuffle around (fun!)
A new approach to diagonalization on a quantum computer
\hat H_1 = e^{s \hat W_1} \hat H e^{-s \hat W_1}
\hat W_k = [D_{k-1},\hat H_{k-1}]
\hat H_k = e^{s \hat W_k} \hat H_{k-1} e^{-s \hat W_k}
\hat H_\text{TFIM} = \sum_{i=1}^{L-1}\hat X_i\hat X_{i+1}+\sum_{i=1}^L \hat Z_i
Double-bracket iteration
\hat W_1 = [\hat D_0,\hat H_0]
\partial_\ell \hat H_\ell = [\hat W_\ell, \hat H_\ell]
\hat W_\ell = [\Delta(\hat H_\ell),\sigma(\hat H_\ell)]
\Delta(\hat H_\ell)
\sigma(\hat H_\ell)
Głazek-Wilson-Wegner flow
Restriction to off-diagonal
Restriction to diagonal
\partial_\ell \|\sigma(\hat H_\ell)\|_{\text{HS}}^2 = -2\|\hat W_\ell\|_{\text{HS}}^2 \le 0
as a quantum algorithm
(addendo: where it's coming from)
\text{Unitary } \hat U_\ell \text{ such that }
\hat W_\ell = [\Delta(\hat H_\ell),\sigma(\hat H_\ell)]
Głazek-Wilson-Wegner flow
\partial_\ell \|\sigma(\hat H_\ell)\|_{\text{HS}}^2 = -2\|\hat W_\ell\|_{\text{HS}}^2 \le 0
as a quantum algorithm
\hat H_\ell = \hat U_\ell \hat H_0 \hat U_\ell^\dagger
\partial_\ell \hat H_\ell = [\hat W_\ell, \hat H_\ell]
(addendo: where it's coming from)
New quantum algorithm for diagonalization
\hat H \mapsto \hat \mathcal H_\ell = \hat \mathcal U_\ell^\dagger \hat H \hat\mathcal U_\ell
\partial_\ell \hat \mathcal H_\ell = [[A(\hat \mathcal H_\ell),B(\hat \mathcal H_\ell)], \hat \mathcal H_\ell]
0
0
0
0
\hat D_s(\hat J) = \prod_{\mu\in\{0,1\}^{\times L}} \hat Z_\mu e^{-i s \hat J/D} \hat Z_\mu
\hat C_s(\hat J) = \left( \hat D_{\sqrt{s/K}}(\hat J)^\dagger \;e^{i\sqrt{s/K}\hat J}\;\hat D_{\sqrt{s/K}}(\hat J)\;e^{-i\sqrt{s/K}\hat J}\right)^K
1) Dephasing
2) Group commutator
3) Frame shifting
\partial_\ell \hat \mathcal H_\ell = [[A(\hat \mathcal H_\ell),B(\hat \mathcal H_\ell)], \hat \mathcal H_\ell]
\hat V_k = \hat C_s(\hat J_{1})\; \hat C_s(\hat J_{2})\ldots \hat C_s(\hat J_{k-1}) \approx e^{-s \hat W_1}\;e^{-s \hat W_2}\ldots e^{-s \hat W_{k-1}}
Fun but painful because probably not possible efficiently
What about other methods?
0
0
0
0
Universal gate set:
single qubit rotations + generic 2 qubit gate
Universal gate set can approximate any unitary
What is a universal quantum computer?
|\psi\rangle = U |00\ldots0\rangle
quantum compiling approximates unitaries with circuits
\Rightarrow U \approx U_c
Quantum compiling
2x2 unitary matrix - use Euler angles
4x4 unitary matrix - use KAK decomposition + 3x CNOT formula
\text{CNOT} = |0\rangle\langle 0|\otimes \begin{pmatrix} 1 & 0\\ 0 &1\end{pmatrix}
+ |1\rangle\langle1 |\otimes \begin{pmatrix} 0 & 1\\ 1 &0\end{pmatrix}
=
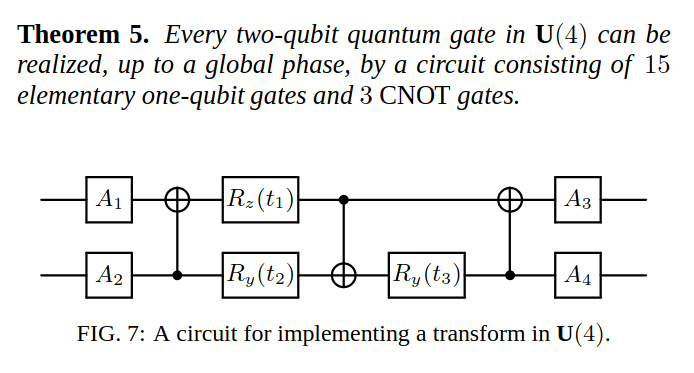
2 qubit unitary
Canonical
KAK decomposition, Brockett's work etc
=
2 qubit unitaries modulo single qubit unitaries are a 3 dimensional torus
Quantum compiling
\(2\) qubits - \(4\times 4\) unitary matrix - use KAK decomposition + \(3\) CNOT formula
Quantum compiling
\(1\) qubit - \(2\times 2\) unitary matrix - use Euler angles
\(n\) qubits - \(2^n\) unitary matrix - use quantum Shannon decomposition + \(O(4^n)\) CNOT formula
Variational quantum eigensolver
0
0
0
0
+
+
+
+
+
This works but is inefficient
This is efficient but doesn't work
Open: fill this gap!
\hat W_k = [\hat D_{k-1},\hat H_{k-1}]
\hat H_k = e^{s_k \hat W_k} \hat H_{k-1} e^{-s_k \hat W_k}
Double-bracket iteration
s_k
Rotation durations:
Input:
\hat H_0
\hat D_k
Diagonal generators:
A new approach to diagonalization on a quantum computer
Great: we can diagonalize
How to quantum compile?
How to quantum?
Group commutator
\hat H \mapsto \hat \mathcal H_\ell = \hat \mathcal U_\ell^\dagger \hat H \hat\mathcal U_\ell
0
0
0
0
Want
\hat H_{k+1} = e^{s \hat W_k} \hat H_k e^{-s \hat W_k}
\hat W_k = [\hat D_k, \hat H_k]
e^{i\sqrt{s_k}\hat D_k}e^{i\sqrt{s_k}\hat H_k}e^{-i\sqrt{s_k}\hat D_k}e^{-i\sqrt{s_k}\hat H_k}= e^{-s[\hat D_k,\hat H_k]} +\hat E^\text{(GC)}
New bound
\|\hat E^\text{(GC)}\| \le 4\|\hat H_0\|\,\|[\hat D_k, \hat H_k]\| s^3
Group commutator during iteration
0
0
0
0
\hat H_{k} = \hat U_k^\dagger \hat H_0 \hat U_k
\hat V_0 = e^{i\sqrt{s_0}\hat D_0}e^{i\sqrt{s_0}\hat H_0}e^{-i\sqrt{s_0}\hat D_0}e^{-i\sqrt{s_0}\hat H_0}
e^{-it \hat H_{k} } = e^{-it \hat U_k^\dagger \hat H_0 \hat U_k}= \hat U_k^\dagger e^{-t \hat H_0} \hat U_k
\hat V_1 = e^{i\sqrt{s_1}\hat D_1}e^{i\sqrt{s_1}\hat H_{1}} e^{-i\sqrt{s_1}\hat D_1}e^{-i\sqrt{s_1}\hat H_{1}}
\hat U_k =\hat V_0 \hat V_1 \ldots \hat V_k
Group commutator during iteration
0
0
0
0
\hat H_{k} = \hat U_k^\dagger \hat H_0 \hat U_k
\hat V_0 = e^{i\sqrt{s_0}\hat D_0}e^{i\sqrt{s_0}\hat H_0}e^{-i\sqrt{s_0}\hat D_0}e^{-i\sqrt{s_0}\hat H_0}
e^{-it \hat H_{k} } = e^{-it \hat U_k^\dagger \hat H_0 \hat U_k}= \hat U_k^\dagger e^{-t \hat H_0} \hat U_k
\hat V_1 = e^{i\sqrt{s_1}\hat D_1}\hat V_{0}^\dagger e^{i\sqrt{s_1}\hat H_{0}}\hat V_0 e^{-i\sqrt{s_1}\hat D_1}\hat V_{0}^\dagger e^{-i\sqrt{s_1}\hat H_{0}}\hat V_0
\hat U_k =\hat V_0 \hat V_1 \ldots \hat V_k
\hat V_k = e^{i\sqrt{s_k}\hat D_k}\hat U_{k-1}^\dagger e^{i\sqrt{s_k}\hat H_{0}}\hat U_{k-1} e^{-i\sqrt{s_k}\hat D_k}\hat U_{k-1}^\dagger
e^{-i\sqrt{s_k}\hat H_{0}}\hat U_{k-1}
\hat W_k = [\hat D_{k-1},\hat H_{k-1}]
\hat H_k = e^{s_k \hat W_k} \hat H_{k-1} e^{-s_k \hat W_k}
Double-bracket iteration
s_k
Rotation durations:
Input:
\hat H_0
\hat D_k
Diagonal generators:
A new approach to diagonalization on a quantum computer
Great: we can diagonalize
How to quantum compile?
Replace by the group commutator
e^{-s[\hat D_k,\hat H_k]}\approx e^{i\sqrt{s}\hat D_k}e^{i\sqrt{s}\hat H_k}e^{-i\sqrt{s}\hat D_k}e^{-i\sqrt{s}\hat H_k}
Group commutator iteration
\hat V_k = e^{i\sqrt{s_k}\hat D_k}e^{i\sqrt{s_k}\hat H_k}e^{-i\sqrt{s_k}\hat D_k}e^{-i\sqrt{s_k}\hat H_k}
\hat H_{k+1} = \hat V_{k}^\dagger\hat H_{k} \hat V_k
\hat V_{k} = e^{-s[\hat D_{k},\hat H_{k}]}
Double-bracket iteration
Double-bracket iteration
Transition from theory to QPUs
How well does it work?
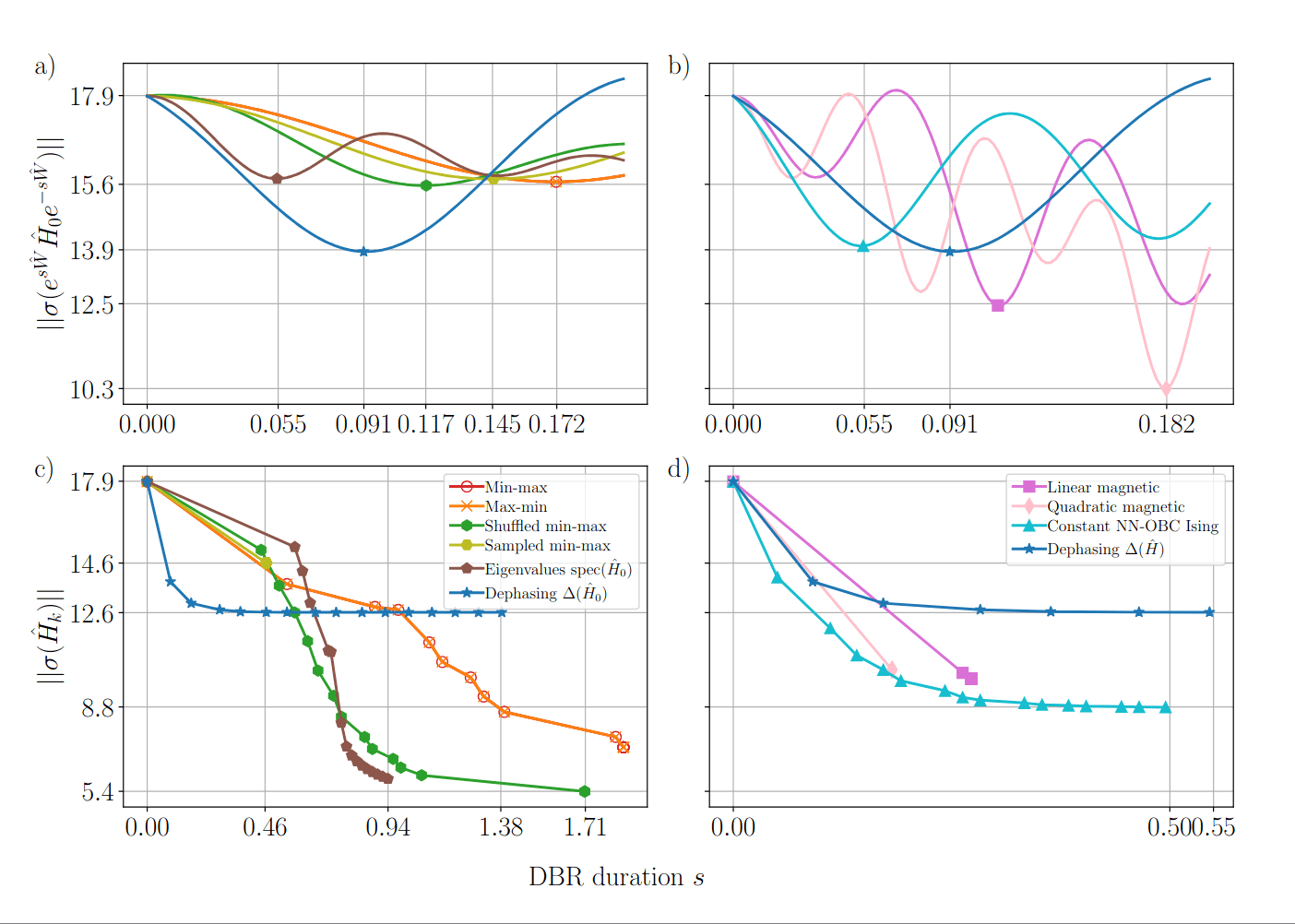
Variational flow example
Notice the steady increase of diagonal dominance.
Variational vs. GWW flow
Notice that degeneracies limit GWW diagonalization but variational brackets can lift them.
GWW for 9 qubits
Notice the spectrum is almost converged.
GWW for 9 qubits
Notice that some of them are essentially eigenstates!
How does it work after warm-start?
10 qubit, 50 layers of CNOT - 99.5% ground state fidelity
\hat A_0 = \sum_{j=1}^L(X_j X_{j+1}+Y_j Y_{j+1}+ Z_j Z_{j+1})
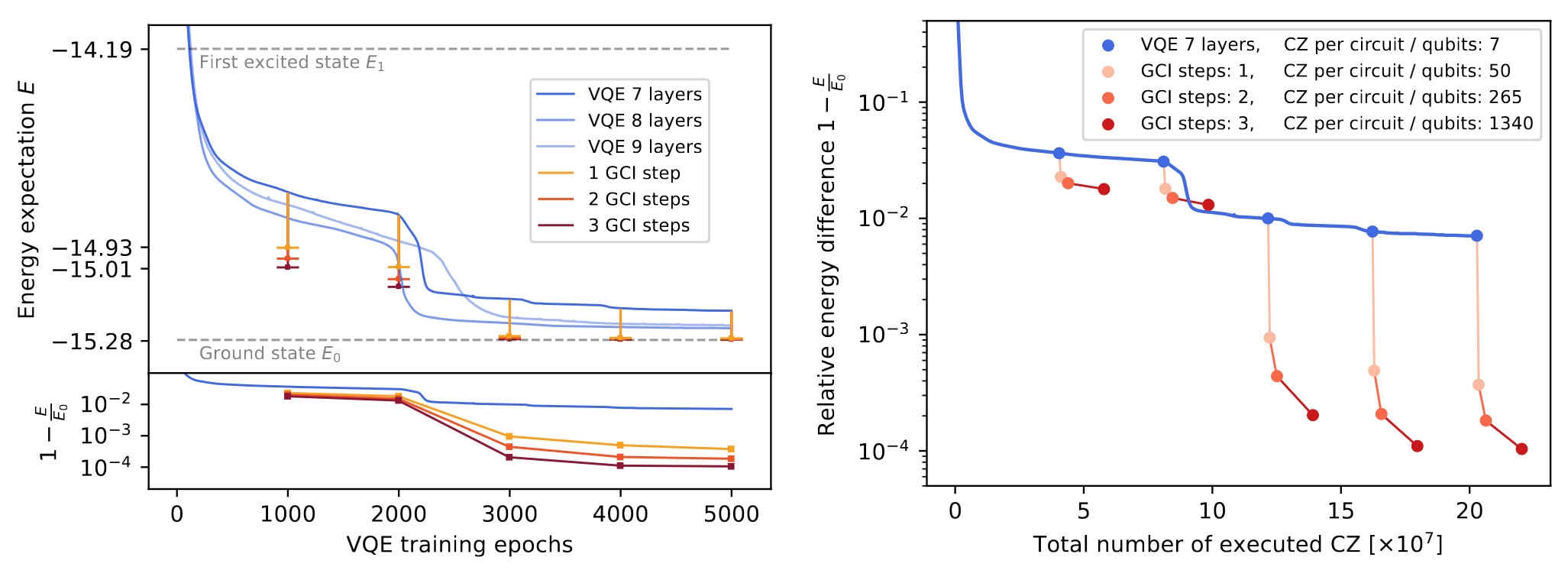
This both works and is efficient
How to interface VQE and DBQA?
Quantum Dynamic Programming
with J. Son, R. Takagi and N. Ng
QDP code structure
Warm-start unitary from variational quantum eigensolver
0
0
0
0
+
+
+
+
+
=
= U_\theta
DBQA input with warmstart
\hat A_0 \rightarrow \hat H_0 = \hat U_\theta^\dagger \hat A_0 \hat U_\theta
V_0 = e^{i\sqrt{s_0}\hat D_0}e^{i\sqrt{s_0}\hat H_0}e^{-i\sqrt{s_0}\hat D_0}e^{-i\sqrt{s_0}\hat H_0}
V_0 = e^{i\sqrt{s_0}\hat D_0}\hat U_\theta^\dagger e^{i\sqrt{s_0}\hat A_0}\hat U_\theta
e^{-i\sqrt{s_0}\hat D_0}\hat U_\theta^\dagger e^{-i\sqrt{s_0}\hat A_0}\hat U_\theta
Use unitarity and get circuit VQE insertions
10 qubit, 50 layers of CNOT - 99.5% ground state fidelity
\hat A_0 = \sum_{j=1}^L(X_j X_{j+1}+Y_j Y_{j+1}+ Z_j Z_{j+1}) \equiv \sum_{j=1}^L\hat A_0^{(j)}
e^{-it\hat A_0} \approx \left( \prod_{j=1}^L e^{-i t\hat A_0^{(j)}/M}\right)^M
e^{-i t\hat A_0^{(j)}/M}=
=
2 qubit unitary
Canonical
Canonical
For quantum compiling we use:
- higher-order group commutators
- higher-order Trotter-Suzuki decomposition
- 3-CNOT formulas
New quantum algorithm for diagonalization
\hat H \mapsto \hat \mathcal H_\ell = \hat \mathcal U_\ell^\dagger \hat H \hat\mathcal U_\ell
\partial_\ell \hat \mathcal H_\ell = [[A(\hat \mathcal H_\ell),B(\hat \mathcal H_\ell)], \hat \mathcal H_\ell]
no qubit overheads
no controlled-unitaries
0
0
0
0
C
0
0
0
0
Simple
=
Easy
Doesn't spark joy :(
Double-bracket quantum algorithm for diagonalization
\hat H \mapsto \hat H_\ell = \hat U_\ell^\dagger \hat H \hat U_\ell
\partial_\ell \hat H_\ell = [[A(\hat H_\ell),B(\hat H_\ell)], \hat H_\ell]
new approach to preparing useful states
0
0
0
0
What else is there?
Linear programming
Matching optimization
Diagonalization
Sorting
QR decomposition
Toda flow
\partial_\ell \hat H_\ell = [[A(\hat H_\ell), B(\hat H_\ell)] , \hat H_\ell]
Double-bracket flow
Runtime-boosting heuristics
Analytical convergence analysis
Group commutator bound
Hasting's conjecture
Relation to other quantum algorithms
Code is available on Github
0
0
0
0
C
Double-bracket quantum algorithms for diagonalization
with J. Son, R. Takagi and N. Ng
\mathcal{E}^{(\mathcal{N},\rho,M)}_{QDP} \coloneqq (\mathcal{E}^{(\mathcal{N},\rho)}_{1/M})^M
Quantum dynamic programming
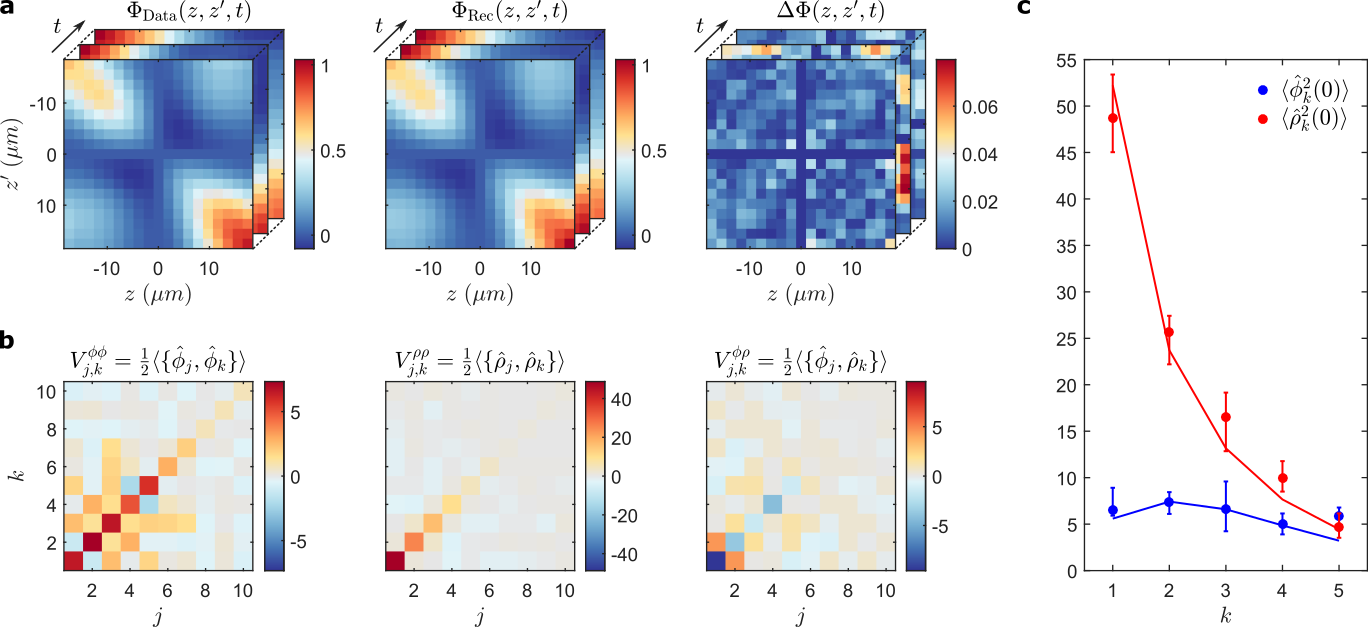
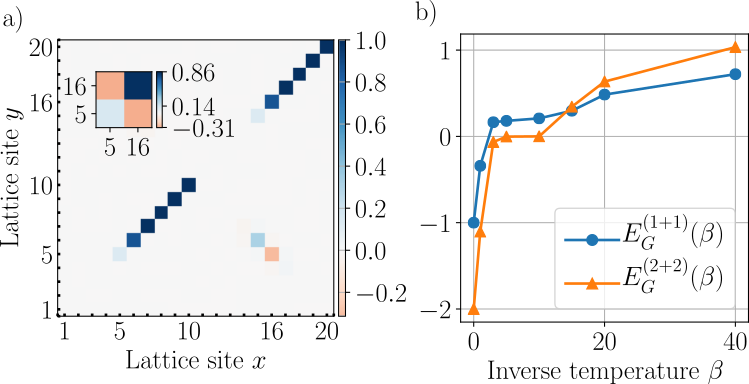
Material science?
0
0
0
0
C
How to dynamically quantum?
Group commutator
\hat H \mapsto \hat \mathcal H_\ell = \hat \mathcal U_\ell^\dagger \hat H \hat\mathcal U_\ell
\partial_\ell \hat \mathcal H_\ell = [[A(\hat \mathcal H_\ell),B(\hat \mathcal H_\ell)], \hat \mathcal H_\ell]
0
0
0
0
Want
\hat H_1 = e^{s \hat W_1} \hat H e^{-s \hat W_1}
\hat W_1 = [\Delta(\hat H),\sigma(\hat H)]
e^{is\Delta(\hat H)}e^{is\hat H}e^{-is\Delta(\hat H)}e^{-is\hat H}= e^{-s^2[\Delta(\hat H),\sigma(\hat H)]} +\hat E^\text{(GC)}
New bound
\|\hat E^\text{(GC)}\| \le 4\|\hat H\|\,\|[\Delta(\hat H),\sigma(\hat H)]\| s^3
Group commutator
\hat H \mapsto \hat \mathcal H_\ell = \hat \mathcal U_\ell^\dagger \hat H \hat\mathcal U_\ell
\partial_\ell \hat \mathcal H_\ell = [[A(\hat \mathcal H_\ell),B(\hat \mathcal H_\ell)], \hat \mathcal H_\ell]
0
0
0
0
Want
\hat H_1 = e^{s \hat W_1} \hat H e^{-s \hat W_1}
\hat W_1 = [\Delta(\hat H),\sigma(\hat H)]
e^{is\Delta(\hat H)}e^{is\hat H}e^{-is\Delta(\hat H)}e^{-is\hat H}= e^{- s^2[\Delta(\hat H),\sigma(\hat H)]} +\hat E^\text{(GC)}
How to get ?
\hat D_s(\hat H) \approx e^{is\Delta(\hat H)}
\hat C_s(\hat J) = \hat D_{\sqrt{s}}(\hat J)^\dagger \; e^{i\sqrt{s}\hat J}\; \hat D_{\sqrt{s}}(\hat J)\; e^{-i\sqrt{s}\hat J}
\approx e^{-s \hat W(\hat J)}
1,
1,
1,
1,
0,
0,
0,
0
Phase flip unitaries
\mu = (
)
N
S
N
S
N
S
N
S
\hat Z
\mathbb 1
\mathbb 1
\otimes
\otimes
\otimes
\otimes
\otimes
\otimes
\otimes
\hat Z
\hat Z
\hat Z
\mathbb 1
\mathbb 1
0,
1,
0,
1,
0,
0,
0,
1
\mu = (
)
1
\otimes
\mathbb 1
\otimes
\mathbb 1
\otimes
\hat Z
\otimes
1
\otimes
\mathbb 1
\otimes
\hat Z
\otimes
\hat Z
N
S
N
S
N
S
Phase flip unitaries
Evolution under dephased generators
\hat H \mapsto \hat H_\ell = \hat U_\ell^\dagger \hat H \hat U_\ell
\partial_\ell \hat H_\ell = [[A(\hat H_\ell),B(\hat H_\ell)], \hat H_\ell]
0
0
0
0
\hat Z_\mu e^{-i s \hat J} \hat Z_\mu = e^{-is \hat Z_\mu \hat J\hat Z_\mu}
\hat D_s(\hat J) \approx \prod_{\mu\in R} \hat Z_\mu e^{-i s \hat J/D} \hat Z_\mu
We can make it efficient:
\Delta(\hat J)= \frac 1 {\dim (\hat J)} \sum_{\mu\in\{0,1\}^{\times L}} \hat Z_\mu \hat J \hat Z_\mu
R \subseteq \{0,1\}^{\times L}
Use unitarity
and repeat many times
New quantum algorithm for diagonalization
\hat H \mapsto \hat \mathcal H_\ell = \hat \mathcal U_\ell^\dagger \hat H \hat\mathcal U_\ell
\partial_\ell \hat \mathcal H_\ell = [[A(\hat \mathcal H_\ell),B(\hat \mathcal H_\ell)], \hat \mathcal H_\ell]
0
0
0
0
\hat D_s(\hat J) = \prod_{\mu\in\{0,1\}^{\times L}} \hat Z_\mu e^{-i s \hat J/D} \hat Z_\mu
\hat C_s(\hat J) = \left( \hat D_{\sqrt{2s/K}}(\hat J)^\dagger \;e^{i\sqrt{2s/K}\hat J}\;\hat D_{\sqrt{2s/K}}(\hat J)\;e^{-i\sqrt{2s/K}\hat J}\right)^K
\hat V_k = \hat V_{k-1}\hat C_s(\hat J_{k-1})
\hat J_{k-1} = \hat V_{k-1}^\dagger \hat H \hat V_{k-1}
1) Dephasing
2) Group commutator
3) Frame shifting
\partial_\ell \hat \mathcal H_\ell = [[A(\hat \mathcal H_\ell),B(\hat \mathcal H_\ell)], \hat \mathcal H_\ell]
\hat V_k = \hat C_s(\hat J_{1})\; \hat C_s(\hat J_{2})\ldots \hat C_s(\hat J_{k-1}) \approx e^{-s \hat W_1}\;e^{-s \hat W_2}\ldots e^{-s \hat W_{k-1}}
Euler's legacy in quantum computing
By Marek Gluza
