Marek Gluza
NTU Singapore
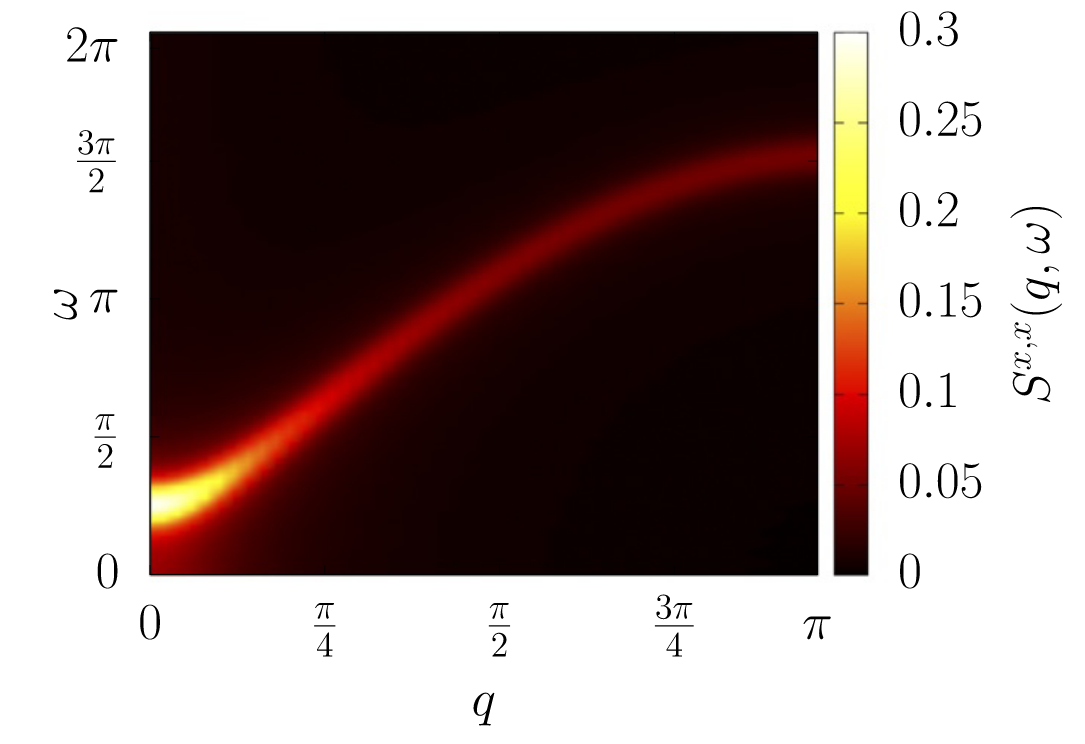
Dynamical structure factor of Rydberg arrays via quantum simulation
How to get this
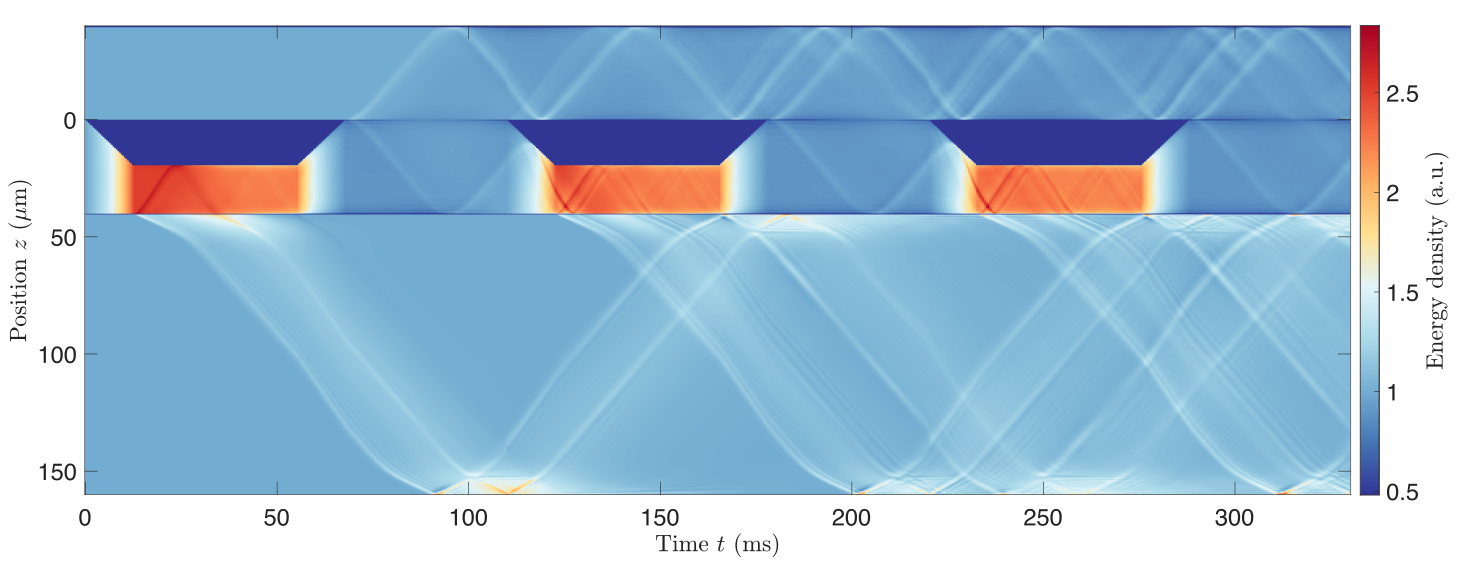
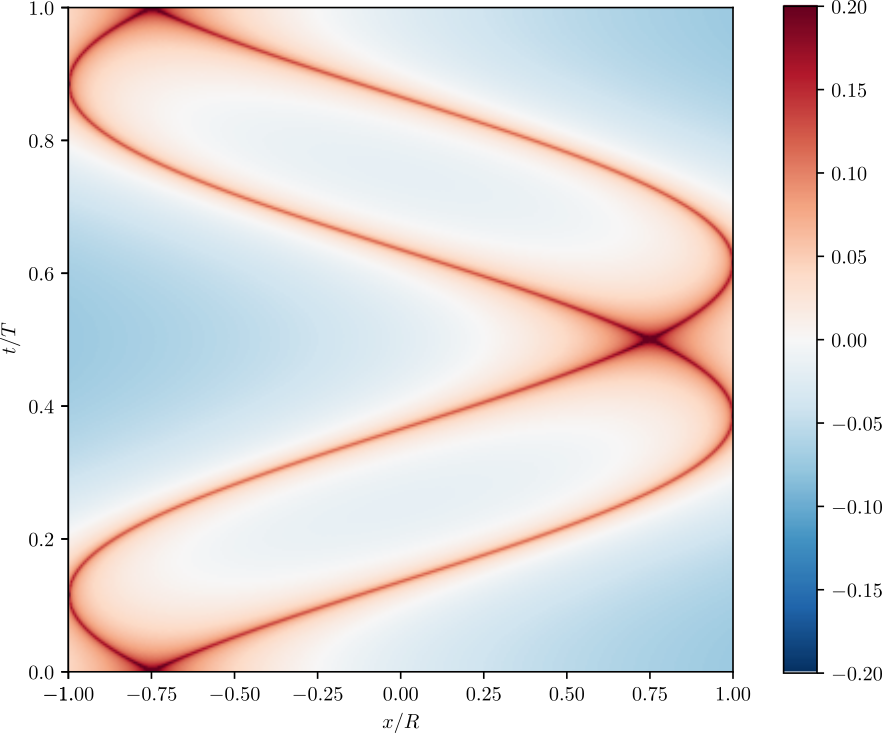
Dynamical structure factor
from this
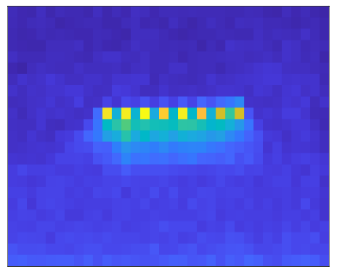
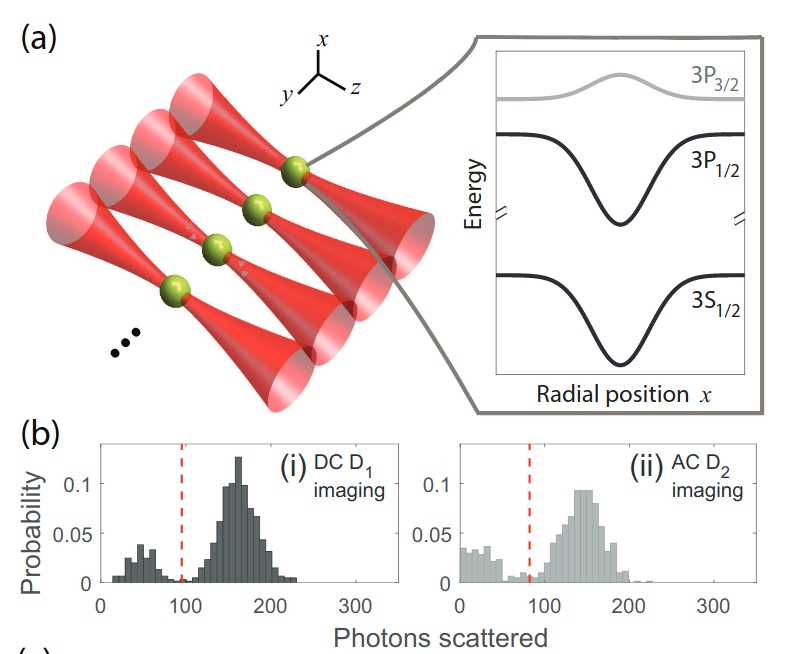
Rydberg
array
Our paper
Laura Baez:
DSF is key for quantum magnetism
Quantum simulators for quantum magnetism need to evaluate DSF!
How will it look for Rydberg atoms?
M. Goihl, J. Haferkamp, J. Bermejo-Vega, J. Eisert
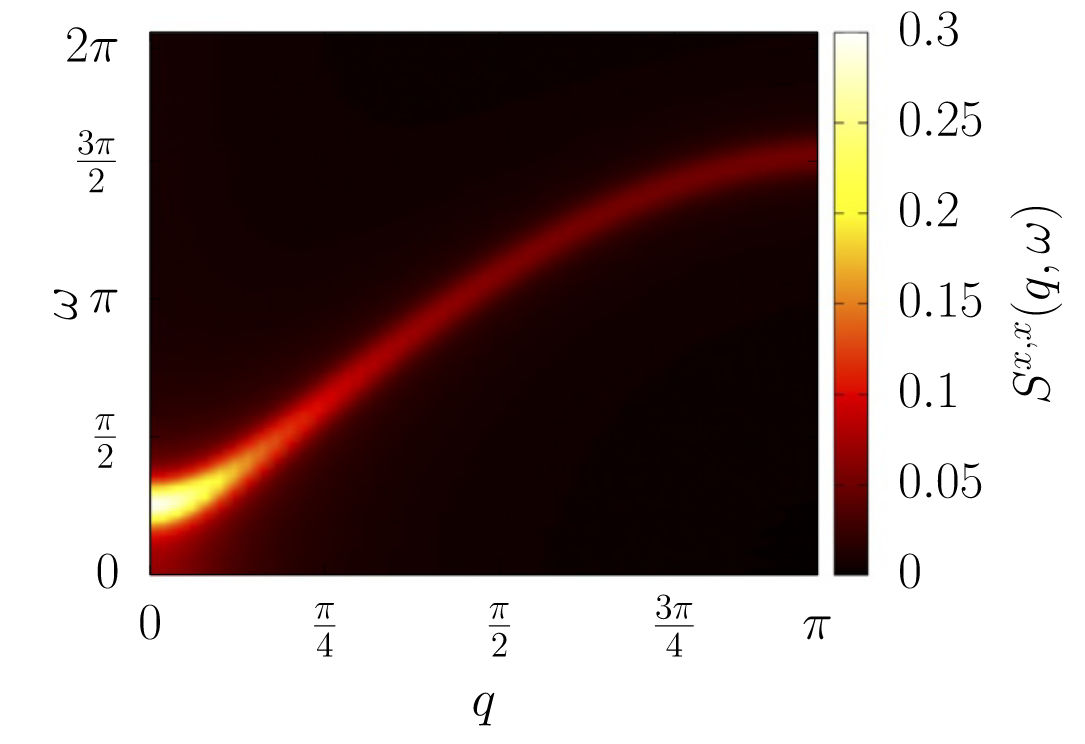
What is DSF?
Frequency
Momentum
Excitation
{
\{
No excitation
=
energy gap
Two-particle continuum
What is DSF?
⟨Ψ∣σjx∣Ψ⟩=21⟨ψ∣σjx∣ψ⟩+Gret(i,j,t)+⟨ψ∣σjxσix(t)σjx∣ψ⟩
\langle \Psi| \sigma^x_j |\Psi\rangle = \frac 12 \langle \psi|\sigma^x_j |\psi\rangle +G^\text{ret}(i,j,t) + \langle \psi|\sigma_j^x \sigma^x_i(t)\sigma^x_j|\psi\rangle
Gret(i,j,t)=⟨ψ∣σix(t)σjx(0)+σjx(0)σix(t)∣ψ⟩
G^\text{ret}(i,j,t) = \langle \psi| \sigma^x_i(t)\sigma_j^x(0)+\sigma_j^x(0)\sigma^x_i(t)|\psi\rangle
Sxx(q,ω)=π1(1+(1+eω/T)−1)Imag[Gret(q,ω)]
S^{xx}(q,\omega) = \frac 1\pi (1 + (1+e^{\omega/ T})^{-1}) \, \text{Imag}[ G^\text{ret}(q,\omega)]
Knap, Demler, et al., https://arxiv.org/abs/1307.0006
Probing real-space and time resolved correlation functions with many-body Ramsey interferometry
How to measure DSF?
Ri(π/4)=21(1−iσix)
R_i(\pi/4) = \frac 1{\sqrt 2}( 1 - i \sigma^x_i)
∣Ψ⟩=U(t)Ri(π/4)∣ψ⟩
|\Psi\rangle = U(t) R_i(\pi/4) |\psi\rangle
U(t)=e−itH
U(t) = e^{-it H}
⟨Ψ∣σjx∣Ψ⟩=21⟨ψ∣(1+iσix)U(t)†σjxU(t)(1−iσix)∣ψ⟩
\langle \Psi| \sigma^x_j |\Psi\rangle = \frac 12 \langle \psi| (1+i\sigma^x_i) U(t)^\dagger \sigma^x_j U(t) (1-i\sigma^x_i) |\psi\rangle
you can measure this if not 0 by symmetry
you can measure this if not 0 by symmetry
⟨Ψ∣σjx∣Ψ⟩=21⟨ψ∣σjx∣ψ⟩+Gret(i,j,t)+⟨ψ∣σjxσix(t)σjx∣ψ⟩
\langle \Psi| \sigma^x_j |\Psi\rangle = \frac 12 \langle \psi|\sigma^x_j |\psi\rangle +G^\text{ret}(i,j,t) + \langle \psi|\sigma_j^x \sigma^x_i(t)\sigma^x_j|\psi\rangle
How to measure DSF?
you can measure this if not 0 by symmetry
you can measure this if not 0 by symmetry
⟨Ψ∣σjx∣Ψ⟩=21⟨ψ∣σjx∣ψ⟩+Gret(i,j,t)+⟨ψ∣σjxσix(t)σjx∣ψ⟩
\langle \Psi| \sigma^x_j |\Psi\rangle = \frac 12 \langle \psi|\sigma^x_j |\psi\rangle +G^\text{ret}(i,j,t) + \langle \psi|\sigma_j^x \sigma^x_i(t)\sigma^x_j|\psi\rangle
Gret(i,j,t)=⟨ψ∣σix(t)σjx(0)+σjx(0)σix(t)∣ψ⟩
G^\text{ret}(i,j,t) = \langle \psi| \sigma^x_i(t)\sigma_j^x(0)+\sigma_j^x(0)\sigma^x_i(t)|\psi\rangle
Sxx(q,ω)=π1(1+(1+eω/T)−1)Imag[Gret(q,ω)]
S^{xx}(q,\omega) = \frac 1\pi (1 + (1+e^{\omega/ T})^{-1}) \, \text{Imag}[ G^\text{ret}(q,\omega)]
Fourier transform in space and time
How to measure DSF?
⟨Ψ∣σjx∣Ψ⟩=21⟨ψ∣σjx∣ψ⟩+Gret(i,j,t)+⟨ψ∣σjxσix(t)σjx∣ψ⟩
\langle \Psi| \sigma^x_j |\Psi\rangle = \frac 12 \langle \psi|\sigma^x_j |\psi\rangle +G^\text{ret}(i,j,t) + \langle \psi|\sigma_j^x \sigma^x_i(t)\sigma^x_j|\psi\rangle
Sxx(q,ω)=π1(1+(1+eω/T)−1)Imag[Gret(q,ω)]
S^{xx}(q,\omega) = \frac 1\pi (1 + (1+e^{\omega/ T})^{-1}) \, \text{Imag}[ G^\text{ret}(q,\omega)]
Fourier transform in space and time
E.g., If want 10% statistical error bar and 60 points (i-j,t) for Fourier transform then with 1 min preparation then it will take about 100 hours to run the experiment
If 1 second preparation then 100 minutes etc.
How well will it work?
HTFIM(J,B)=J∑i,j∣i−j∣−ασixσjx+B∑iσiz
H^\text{TFIM}(J,B) = J\sum_{i,j} |i-j|^{-\alpha} \sigma^x_i \sigma^x_j + B\sum_i \sigma^z_i
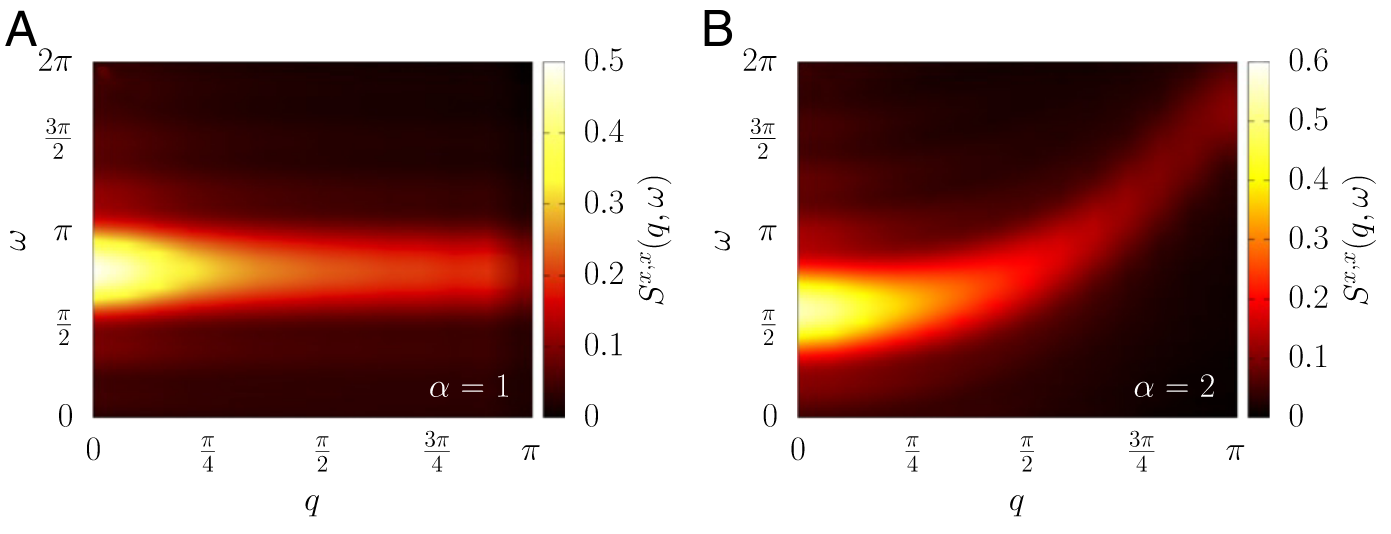
How well will it work?
HTFIM(J,B)=J∑i,j∣i−j∣−ασixσjx+B∑iσiz
H^\text{TFIM}(J,B) = J\sum_{i,j} |i-j|^{-\alpha} \sigma^x_i \sigma^x_j + B\sum_i \sigma^z_i
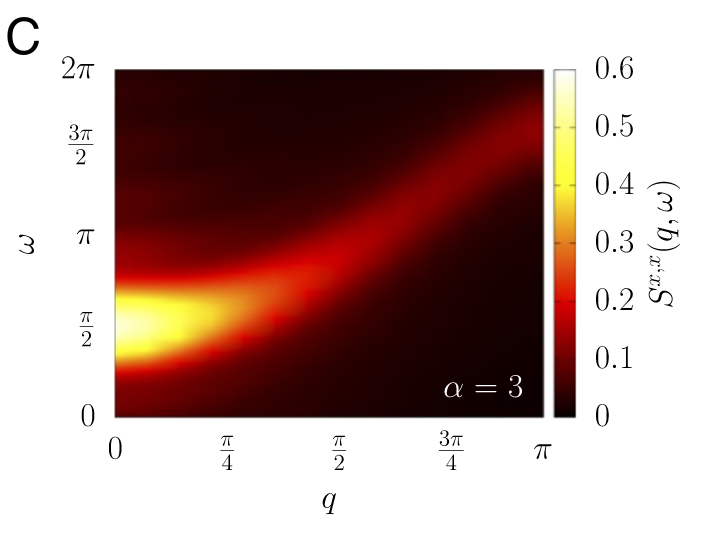
Imperfections:
finite-size effects
finite quench duration
finite Fourier transform
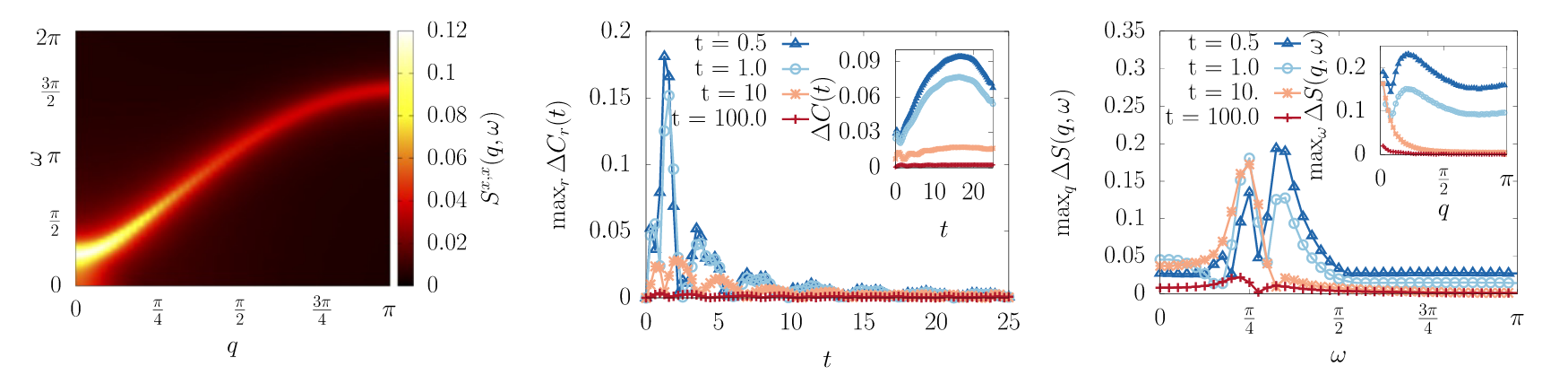
Imprefection if state not the ground-state but finite-time adiabatic preparation
Correlation deviation continuously decreased and so DSF converges (quantitatively) fairly soon
(qualitatively: ok!)
HTFIM(J,B)=J∑iσixσi+1x+B∑iσiz
H^\text{TFIM}(J,B) = J \sum_{i} \sigma^x_i \sigma^x_{i+1} + B\sum_i \sigma^z_i
⟨Experimental troubles⟩
\langle \text{Experimental troubles} \rangle
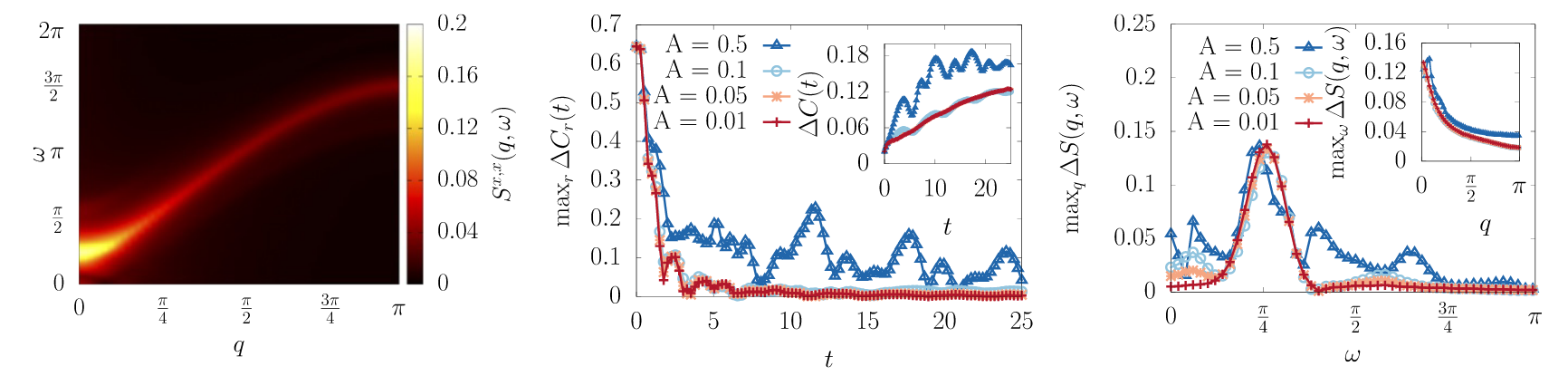
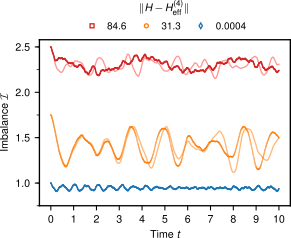
Imprefection if lattice is breathing
Correlation deviation is persistent and so DSF also deviates (quantitatively)
(qualitatively: ok!)
J=J0(1+AcosΩt)
J = J_0 (1 + A \cos \Omega t)
HTFIM(J,B)=J∑iσixσi+1x+B∑iσiz
H^\text{TFIM}(J,B) = J \sum_{i} \sigma^x_i \sigma^x_{i+1} + B\sum_i \sigma^z_i
⟨Experimental troubles⟩
\langle \text{Experimental troubles} \rangle
Complexity theory
raison d'être quantum simulation: compute what is hard to compute
it would be nice if the quantum simulated outcomes are useful
P: Runs easily
BPP: Often runs easily
BQP: Often quantums easily
NP: Optimizes easily
QMA
P: Runs easily
BPP: Often runs easily
BQP: Often quantums easily
NP: Optimizes easily
"hardness( DSF approximation )"
=
"run( quantum computation )"
What else is there?
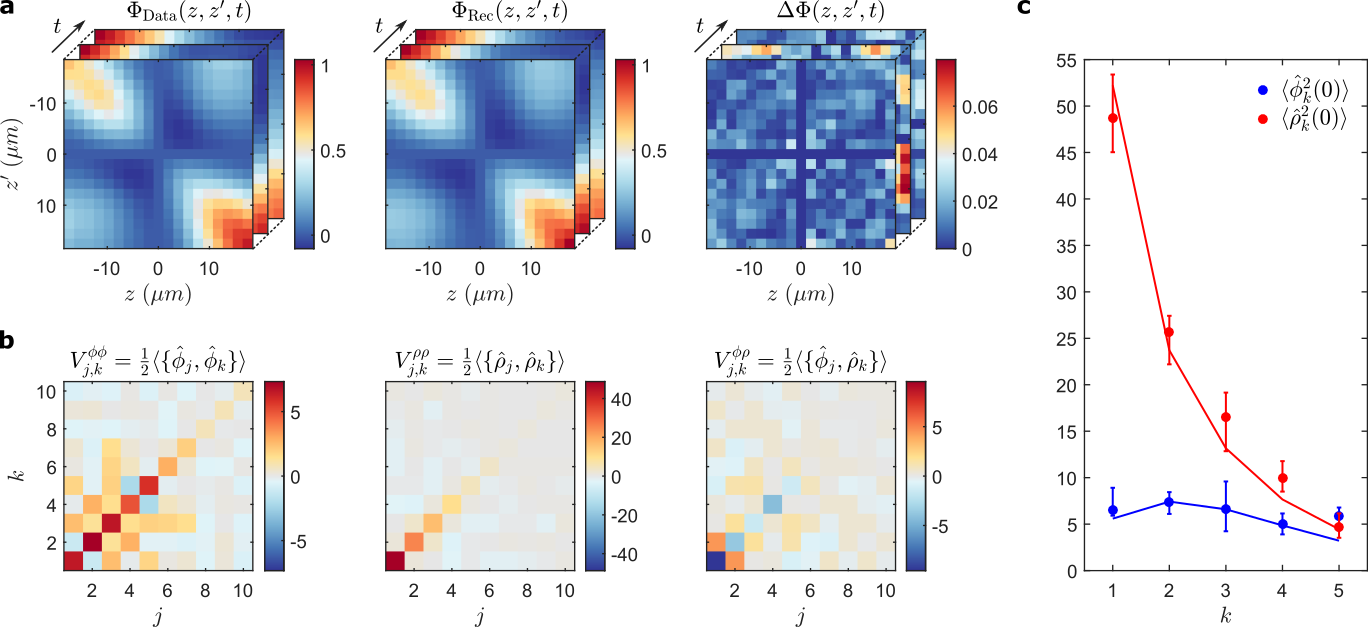
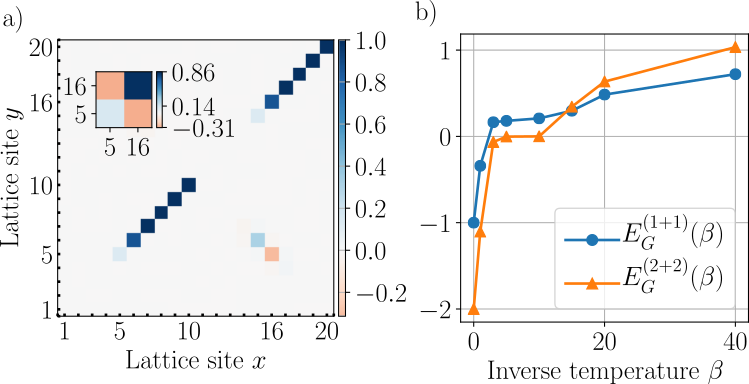
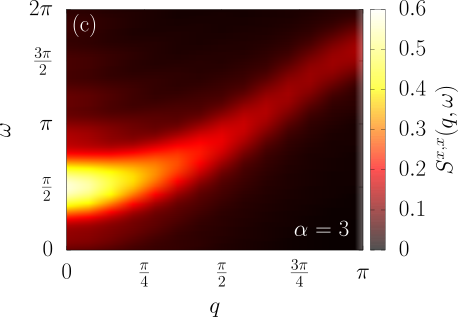
Material science?
0
0
0
0
C
Diagonalization quantum algorithm
DSF of Rydberg arrays
Phonon tomography
Optical lattice tomography
New quantum algorithm for diagonalization
\hat H \mapsto \hat \mathcal H_\ell = \hat \mathcal U_\ell^\dagger \hat H \hat\mathcal U_\ell
\partial_\ell \hat \mathcal H_\ell = [[A(\hat \mathcal H_\ell),B(\hat \mathcal H_\ell)], \hat \mathcal H_\ell]
no qubit overheads
no controlled-unitaries
0
0
0
0
C
0
0
0
0
Simple
=
Easy
Doesn't spark joy :(
⟨ϕ^k2(t)⟩=cos2(ωkt)⟨ϕk2(0)⟩+sin2(ωkt)⟨δρ^k2(0)⟩
\langle\hat \phi_k^2(t)\rangle= \cos^2(\omega_k t) \langle \phi_k^2(0)\rangle \\
\quad\quad\quad\quad\quad+\sin^2(\omega_k t) \langle \delta\hat \rho_k^2(0)\rangle
δρ^
\delta \hat\rho
⟨ϕ^2(t)⟩
\langle\hat \phi^2(t)\rangle
⟨δρ^2(0)⟩=0?
\langle\delta\hat \rho^2(0)\rangle =0?
⟨ϕ^2(0)⟩
\langle \hat \phi^2(0)\rangle
ϕ^
\hat \phi
Ask me anytime:
0
0
0
0
C
Fidelity witnesses
Tomography optical lattices
Tomography phonons
Proving statistical mechanics
Quantum simulating DSF
Holography in tensor networks
PEPS contraction average #P-hard
Quantum field machine
MBL l-bits
(click links at slides.com/marekgluza
Marek Gluza NTU Singapore Dynamical structure factor of Rydberg arrays via quantum simulation https://arxiv.org/abs/1912.06076 M. Goihl, J. Haferkamp, J. Bermejo-Vega, J. Eisert L. Baez
Dynamical structure factor of Rydberg arrays
By Marek Gluza
Dynamical structure factor of Rydberg arrays
- 460
