Mechanisms for the emergence of Gaussian correlations
Marek Gluza
presenting based on collaboration with
T. Schweigler, M. Tajik, J. Sabino, F. Cataldini, S-C. Ji, F. Moller, B. Rauer, J. Schmiedmayer, J. Eisert, S. Sotiriadis
NTU Singapore
Join in for a science popularization experiment:
archiving our temporal thoughts about time
Today will be about
Using quantum simulator read-out
to better understand observed physics
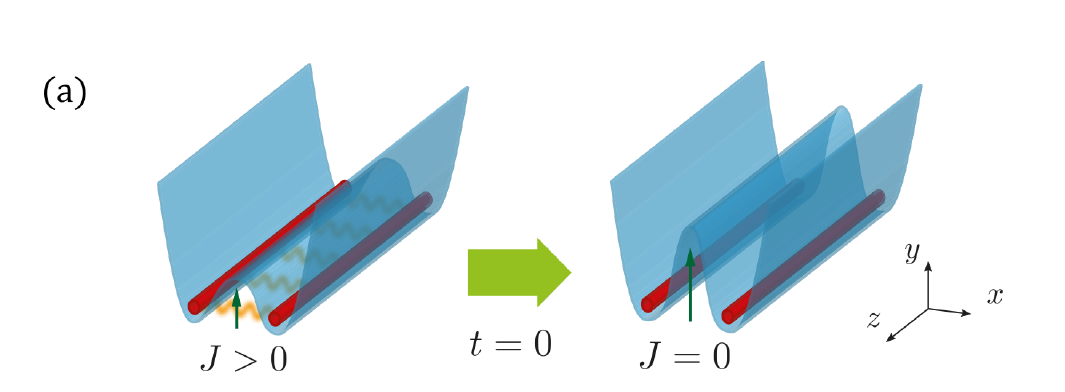
The physical system
Can we develop
continuous field quantum simulators?
- Representation theory: Quantum information?
- Continuum limits: BQP and QMA or more?
- Are nanowires computationally hard to simulate?
What do we know is difficult?
SM
Fundamental
Universal
Effective
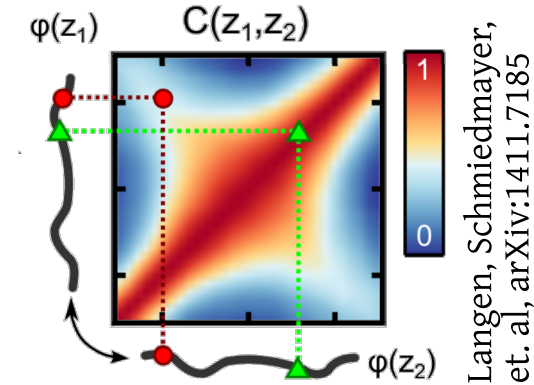
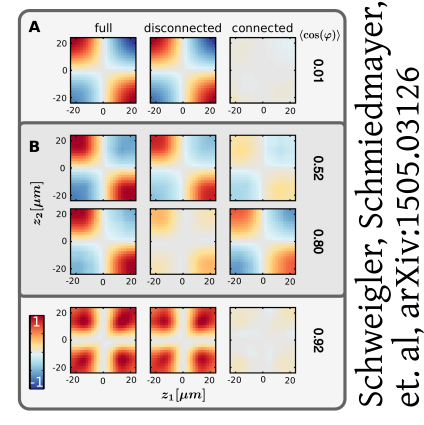
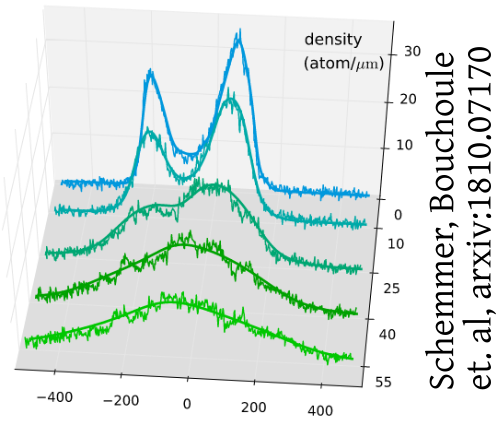
Non-thermal
steady states
Sine-Gordon
thermal states
Atomtronics
Generalized hydrodynamics
Recurrences
Some highlights:
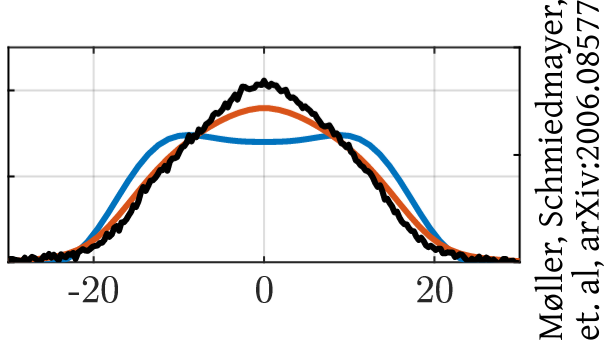
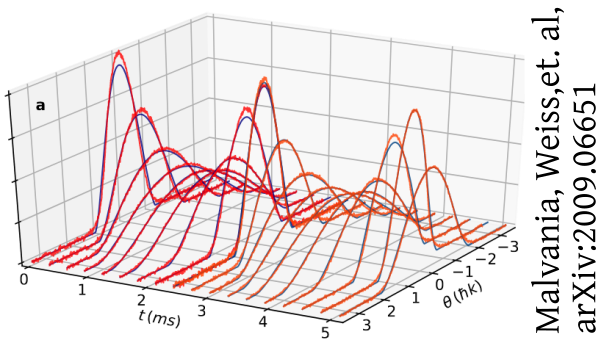
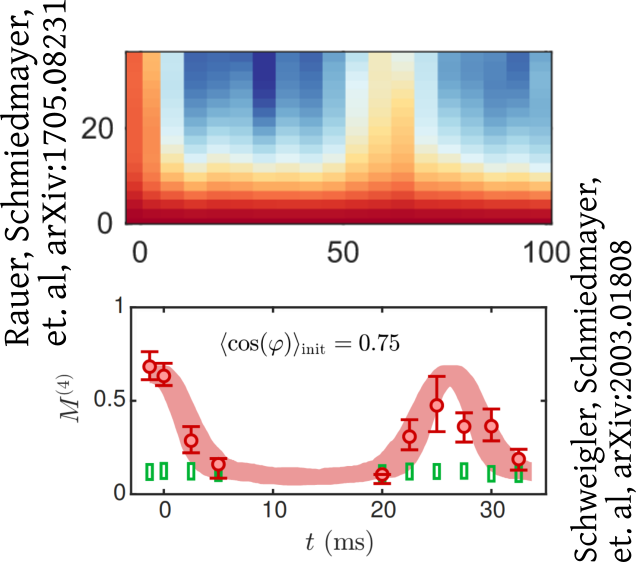
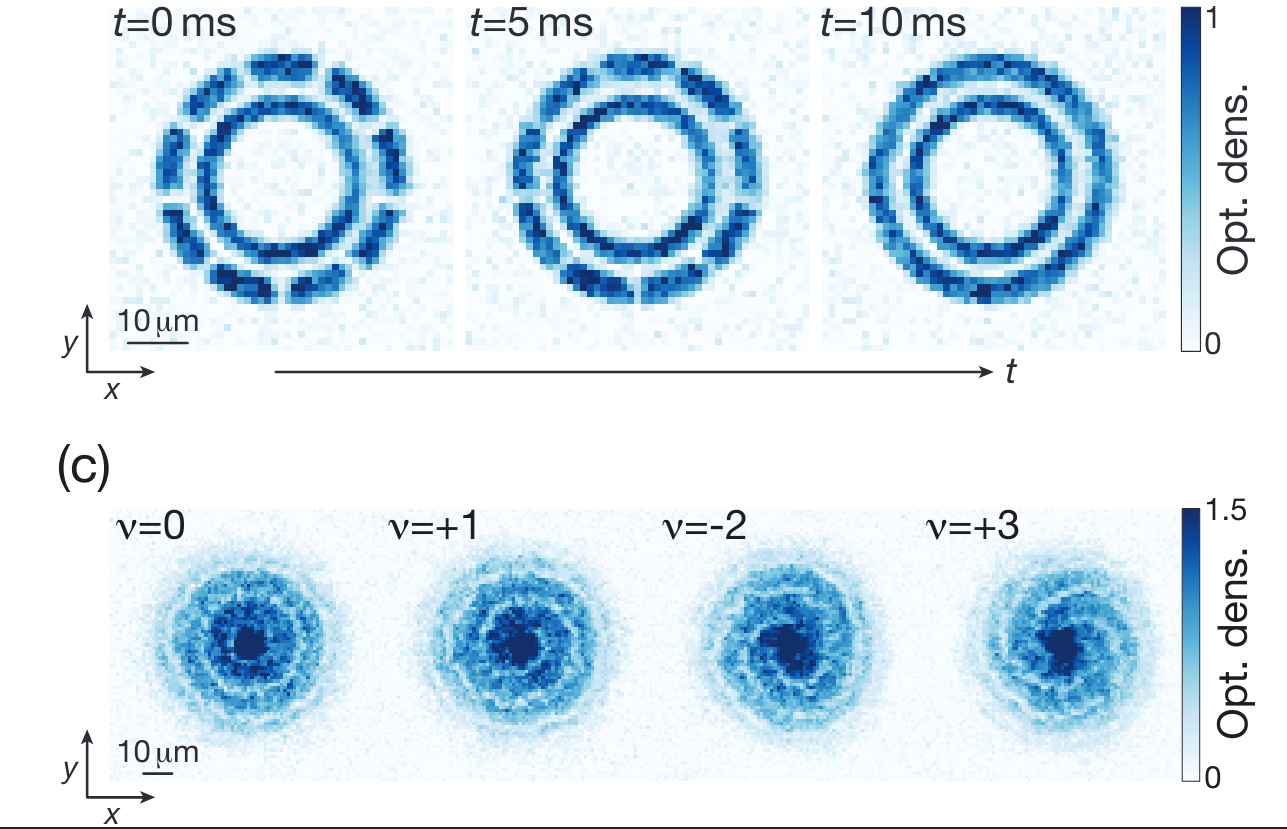
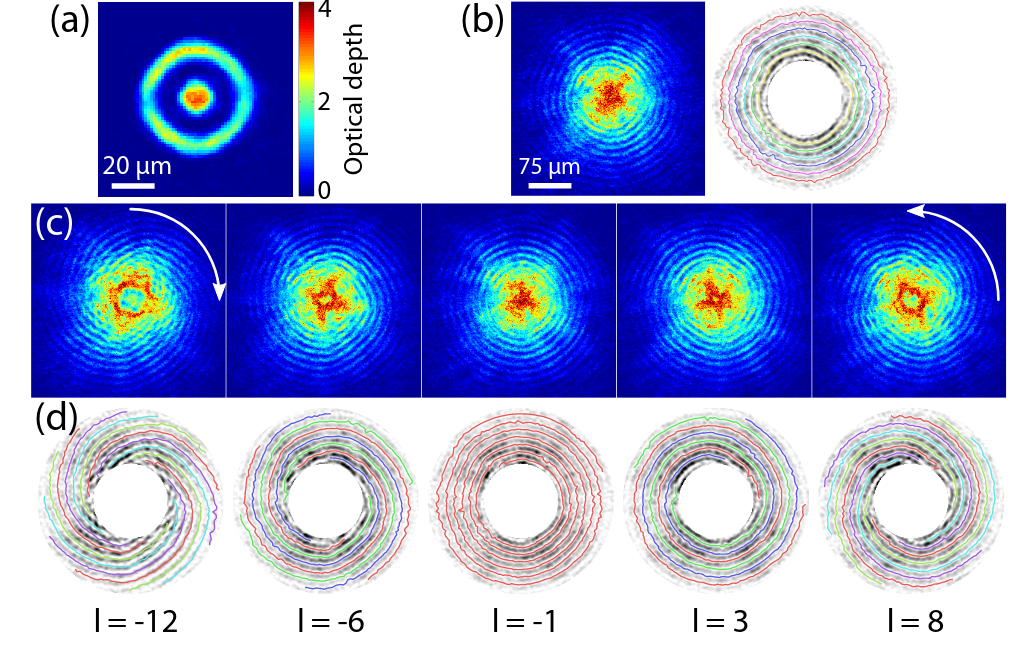
Amin Tajik on Friday
Δz
\Delta z
Interferometry
measures velocities
Δz
\Delta z
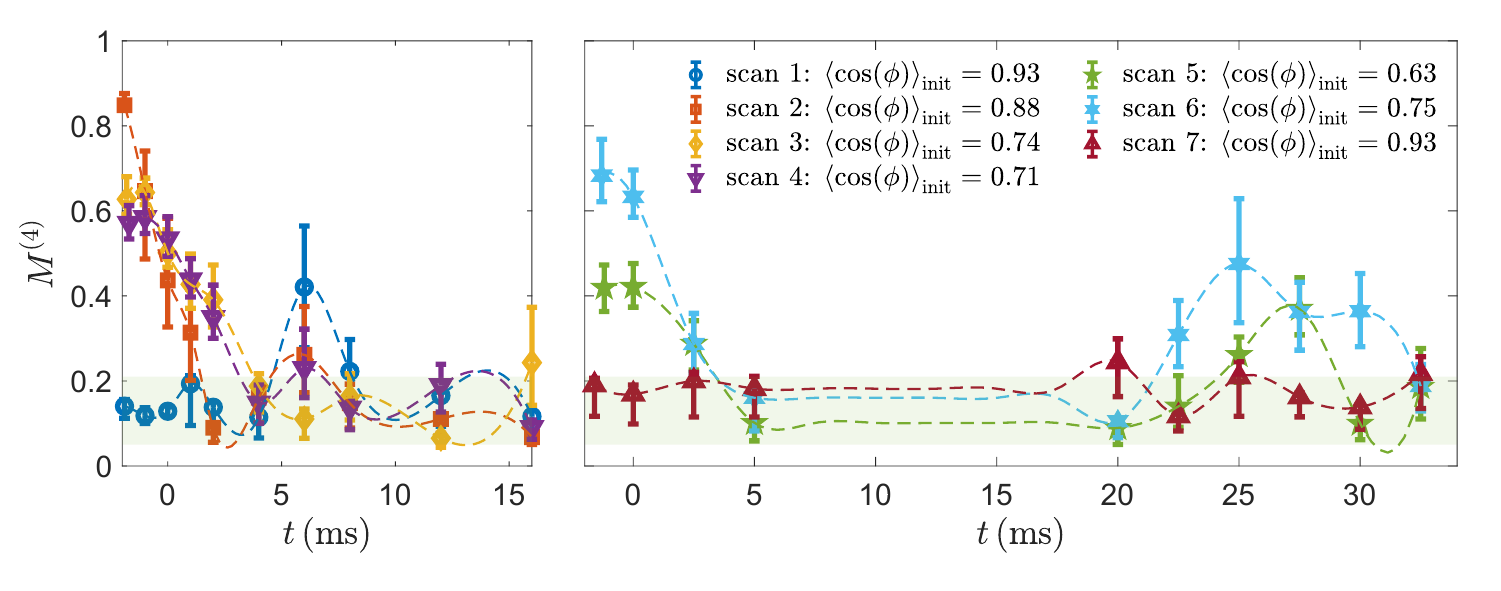
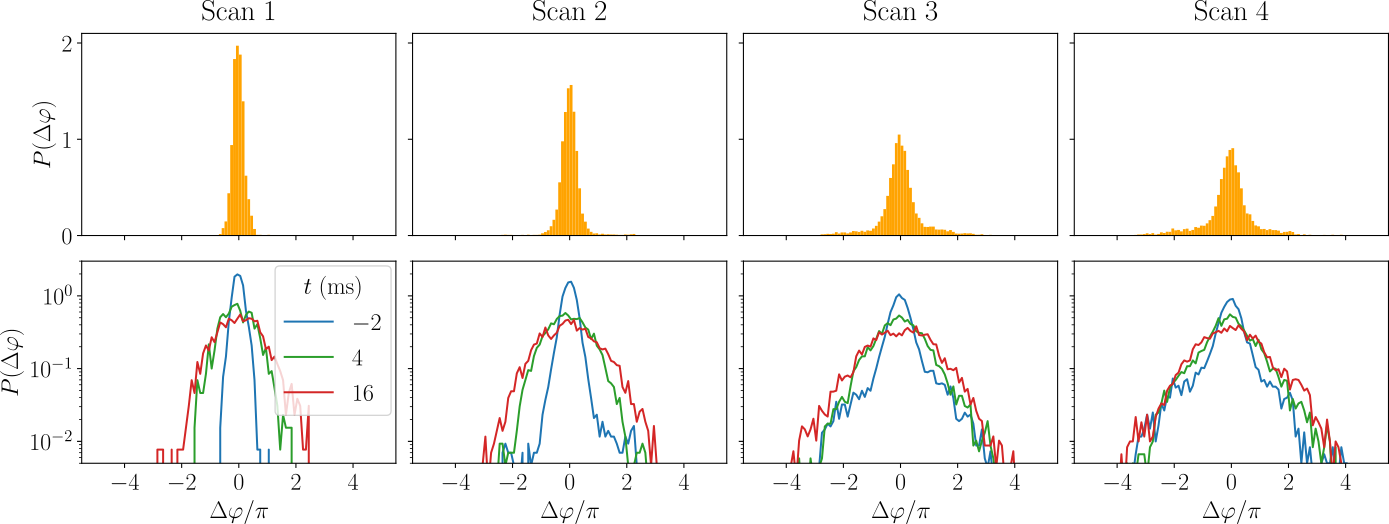
Initial non-Gaussianity decays
Why does it decay?
The system is isolated
Initial non-Gaussianity decays
Why does it revive?
The system is isolated
Then it revives
See persistence of non-Gaussianity in Rydberg arrays: Deger, Daniel, Papić, Pachos arxiv:2306.12210
X=n1∑i=1nX(i)
X = \frac 1 {\sqrt n} \sum_{i=1}^n X^{(i)}
a^x(t)≈vt1∑y=1vteiϕx,y(t)a^y(0)
\hat a_x(t) \approx \frac 1 {\sqrt {vt}} \sum_{y=1}^{vt} e^{i\phi_{x,y}(t)} \hat a_y(0)
Single-particle Green's functions that behave like this: Gaussify
(Think: Central limit theorem)
Phase fluctuations
Phase derivative correlations
increase with distance
decay but sizeable
Effective light cone
not dispersive
Conclusion: Spatial scrambling unlikely in this experiment
⟨x^4⟩=⟨x^2⟩2
\langle \hat x^4\rangle \neq \langle \hat x^2\rangle^2
⟨p^4⟩=⟨p^2⟩2
\langle \hat p^4\rangle = \langle \hat p^2\rangle^2
but
⟨x^2⟩≪⟨p^2⟩
\langle \hat x^2\rangle \ll \langle \hat p^2\rangle
x^(t)=cos(ωt)x^(0)+sin(ωt)p^(0)
\hat x(t) = \cos(\omega t) \hat x(0) +\sin(\omega t)\hat p(0)
⟨x^(t)4⟩≈(ωt)4⟨p^2⟩2
\langle \hat x(t)^4\rangle \approx (\omega t)^4 \langle \hat p^2\rangle^2
⟨x^(π/2ω)4⟩=⟨p^2⟩2
\langle \hat x(\pi / 2 \omega)^4\rangle = \langle \hat p^2\rangle^2
Think: transmuting the cumulant
Canonical decoupling:
Dominant Gaussian sector:
Quadrature rotation:
Gaussification by transmutation:
Classical field approximation conjecture: general at high temperature?
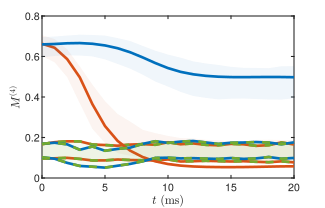
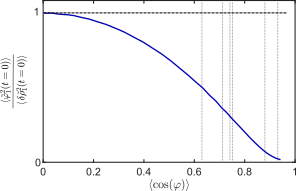
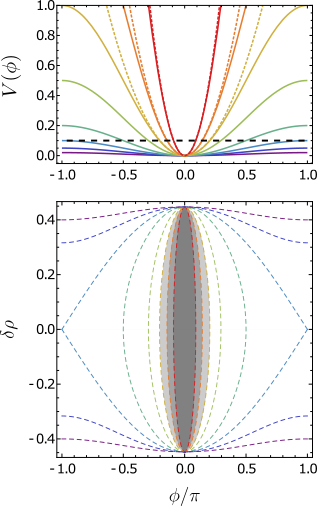
Conclusion: Canonical transmutation likely in this experiment
Conclusion: Canonical transmutation likely in this experiment
Conclusion: Spatial scrambling unlikely in this experiment
T. Schweigler, M. Tajik, J. Sabino, F. Cataldini, S-C. Ji, F. Moller, B. Rauer, J. Schmiedmayer, J. Eisert, S. Sotiriadis
Join in for a science popularization experiment:
archiving our temporal thoughts about time
How?
1d gases
Inside: atoms
Outside: wavepackets
hydrodynamics
Energy of phonons
E
E
E
E
E
E
E
E
H^TLL=∫dz[2mℏ2nGP∂zφ^2+gδϱ^2]
\hat H_\text{TLL} = \int \text{d}z\left[ \frac{\hbar^2n_{GP}}{2m}\partial_z\hat\varphi^2+g\delta\hat\varrho^2\right]
δϱ
\delta\varrho
∂zφ
\partial_z\varphi
∂zφ
\partial_z\varphi
≪
\ll
δϱ
\delta\varrho
≪
\ll
Tomonaga-Luttinger liquid
Gluza&Sabino&Vitaliagno&Ng, Huber&Schmiedmayer&Eisert, arixv:2006.01177
Quantum field refrigerators in the TLL model:
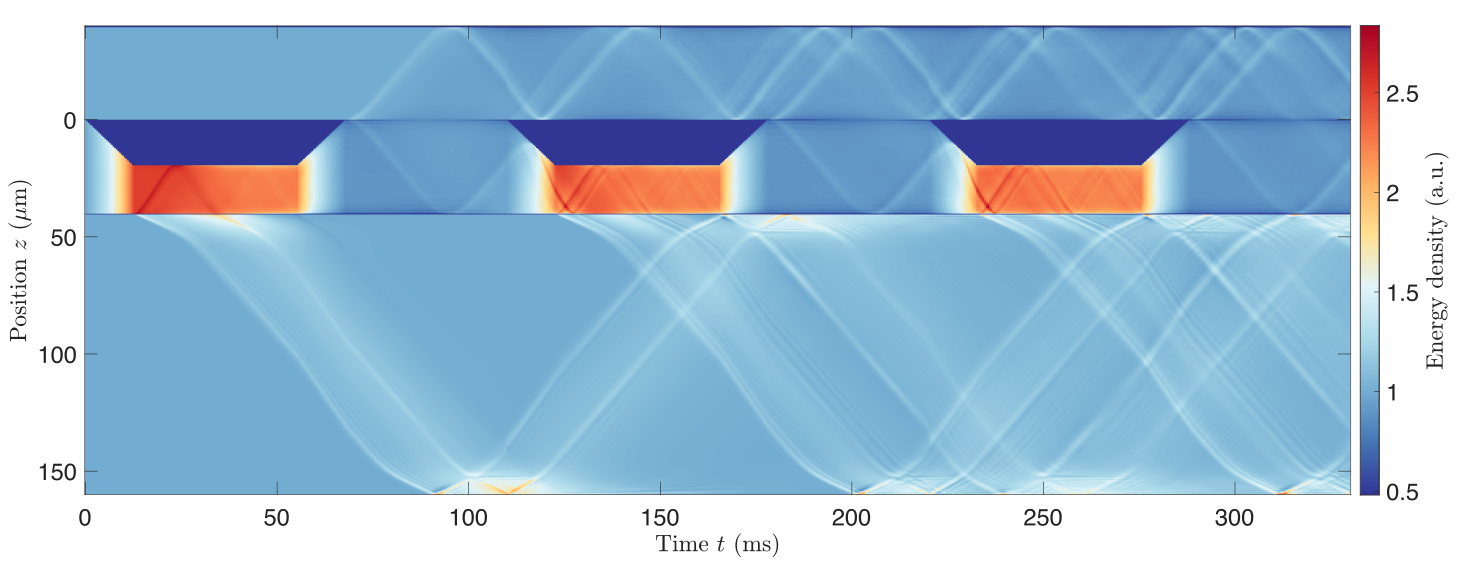
System
Piston
Bath
Bath with excitations
System cooled down
Breaking of the Huygens-Fresnel principle
in the inhomogenous TLL model:
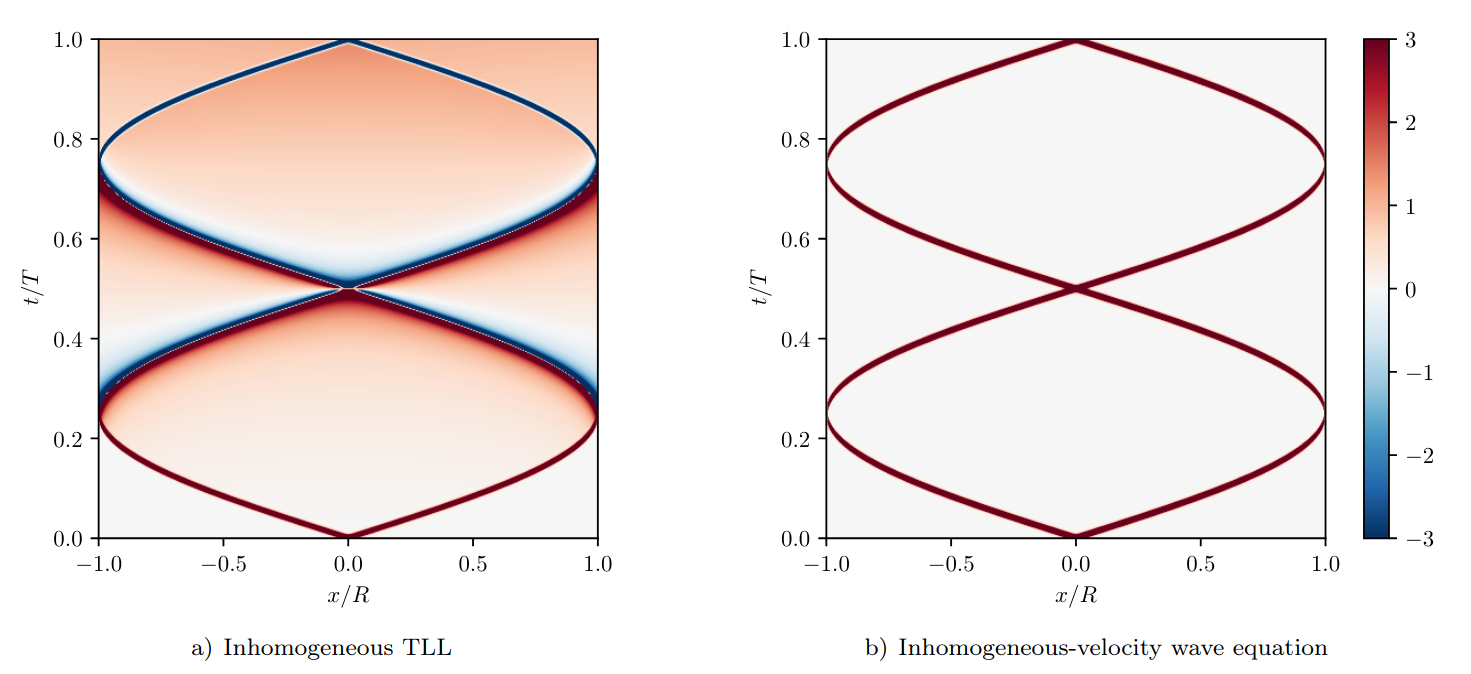
Gluza, Moosavi, Sotiriadis, arxiv:2104.07751
Why?
What?
What about correlations?
z
z
z′
z'
⟨Δφ^(z)Δφ^(z′)⟩/Δz2≈⟨∂zφ^(z)∂zφ^(z′)⟩
\langle \Delta\hat\varphi(z)\Delta\hat\varphi(z')\rangle/ \Delta z^2 \approx \langle \partial_z\hat\varphi(z)\partial_z\hat\varphi(z')\rangle
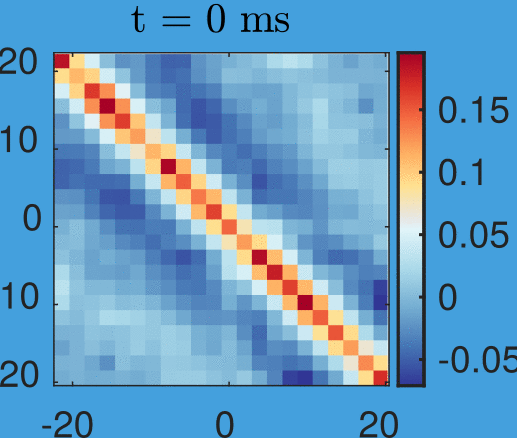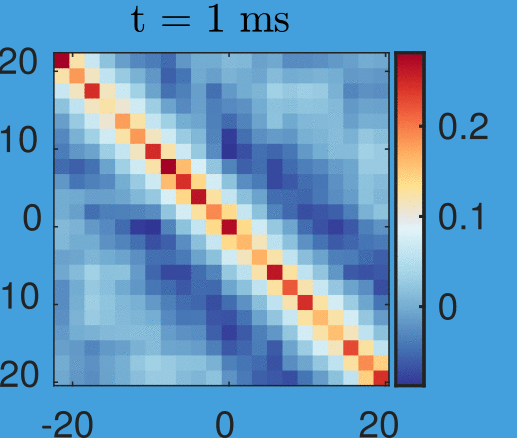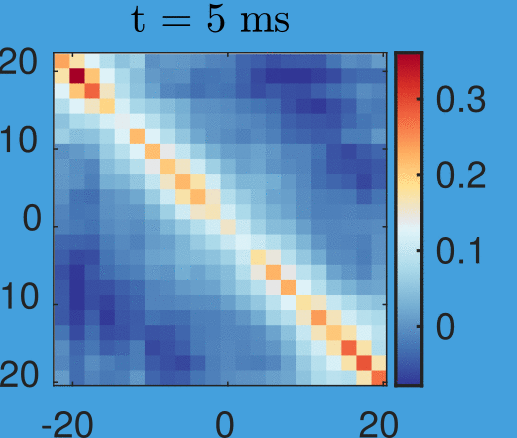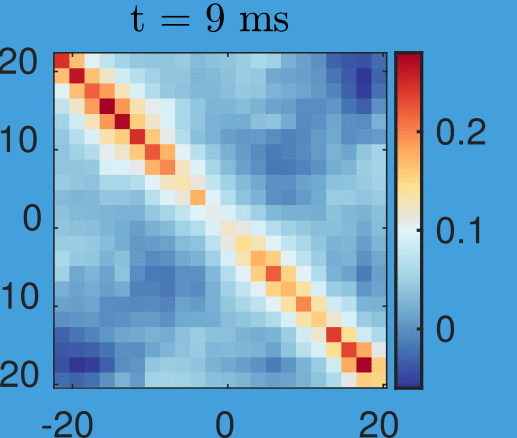
Velocity correlations:
⟨Δφ^(z)Δφ^(z′)⟩/Δz2<0
\langle \Delta\hat\varphi(z)\Delta\hat\varphi(z')\rangle/ \Delta z^2 <0
Anti-correlation:
Left moves opposite to right
z
z
z′
z'
Velocity correlations
z
z
z′
z'
C(z,z′)≈Δz2⟨Δφ^(z)Δφ^(z′)⟩
C(z,z') \approx \frac{\langle \Delta\hat\varphi(z)\Delta\hat\varphi(z')\rangle}{ \Delta z^2 }
And with anti-correlation:
C(z,z′)≈Δz2⟨Δφ^(z)Δφ^(z′)⟩
C(z,z') \approx \frac{\langle \Delta\hat\varphi(z)\Delta\hat\varphi(z')\rangle}{ \Delta z^2 }
C(z,z′,t)≈Δz2⟨Δφ^(z,t)Δφ^(z′,t)⟩
C(z,z',t) \approx \frac{\langle \Delta\hat\varphi(z,t)\Delta\hat\varphi(z',t)\rangle}{ \Delta z^2 }
New data by M. Tajik, J. Schmiedmayer
Time step: 1ms
Simplicity arising from a quench:
Data by M. Tajik, J. Schmiedmayer
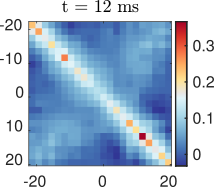
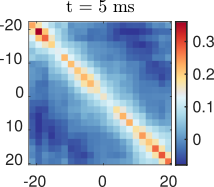
What?
What about quantum correlations?
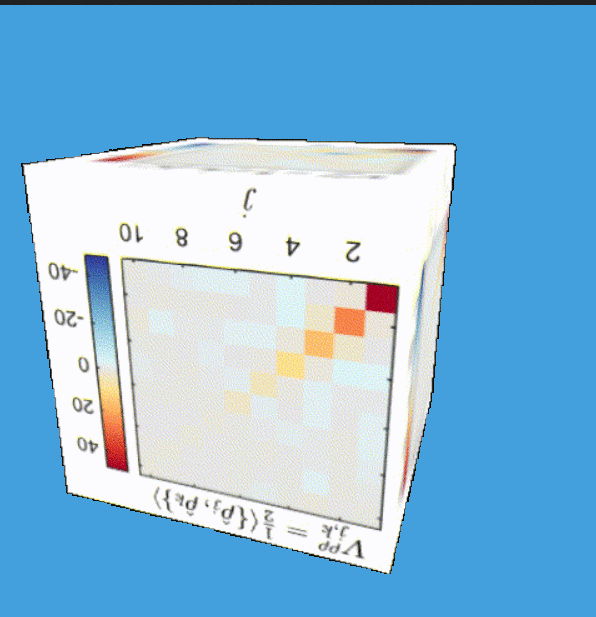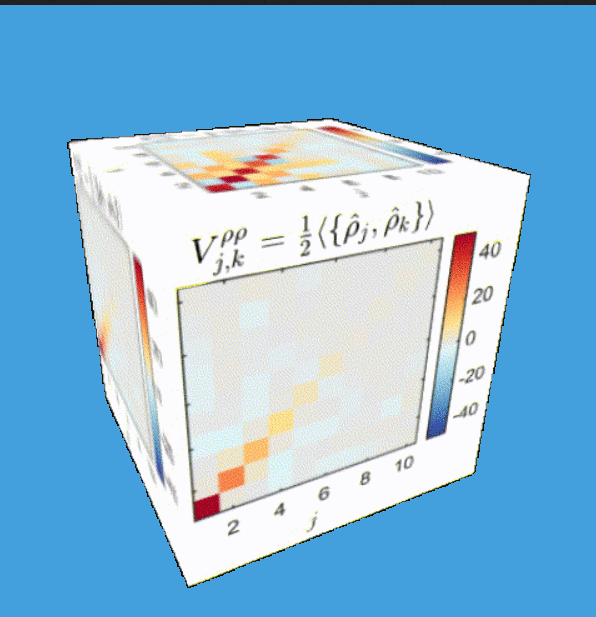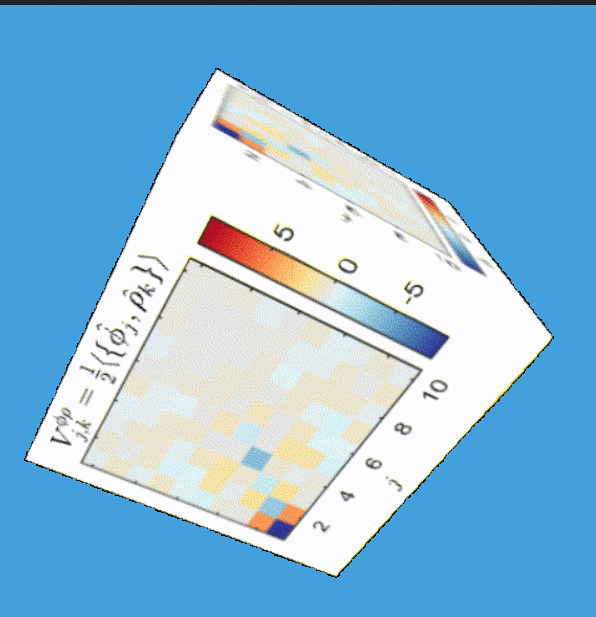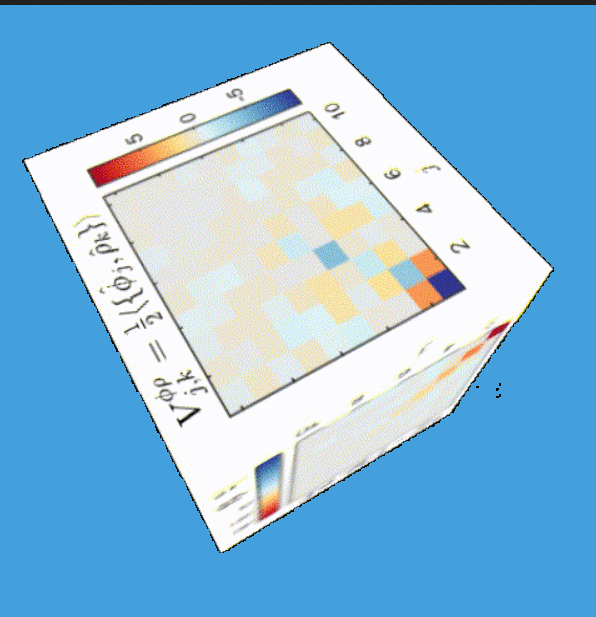
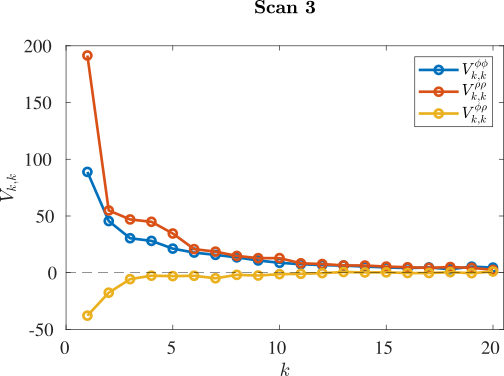
Tomography for phonons
H^TLL=∫dz[2mℏ2nGP∂zφ^2+gδϱ^2]
\hat H_\text{TLL} = \int \text{d}z\left[ \frac{\hbar^2n_{GP}}{2m}\partial_z\hat\varphi^2+g\delta\hat\varrho^2\right]
H^TLL=∑k>02ℏωk(ϕk2+δρ^k2)+gρ02
\hat H_\text{TLL} = \sum_{k>0} \frac {\hbar \omega_k}2 (\phi_k^2+\delta\hat\rho_k^2) + g\rho_0^2
⟨ϕ^k2(t)⟩=cos2(ωkt)⟨ϕk2(0)⟩+sin2(ωkt)⟨δρ^k2(0)⟩
\langle\hat \phi_k^2(t)\rangle= \cos^2(\omega_k t) \langle \phi_k^2(0)\rangle \\
\quad\quad\quad\quad\quad+\sin^2(\omega_k t) \langle \delta\hat \rho_k^2(0)\rangle
δρ^
\delta \hat\rho
⟨ϕ^2(t)⟩
\langle\hat \phi^2(t)\rangle
⟨δρ^2(0)⟩=0?
\langle\delta\hat \rho^2(0)\rangle =0?
⟨ϕ^2(0)⟩
\langle \hat \phi^2(0)\rangle
ϕ^
\hat \phi
Gluza, Schmiedmayer&Eisert, et al, arxiv:1807.04567
Gluza, Eisert, arxiv:2005.09000
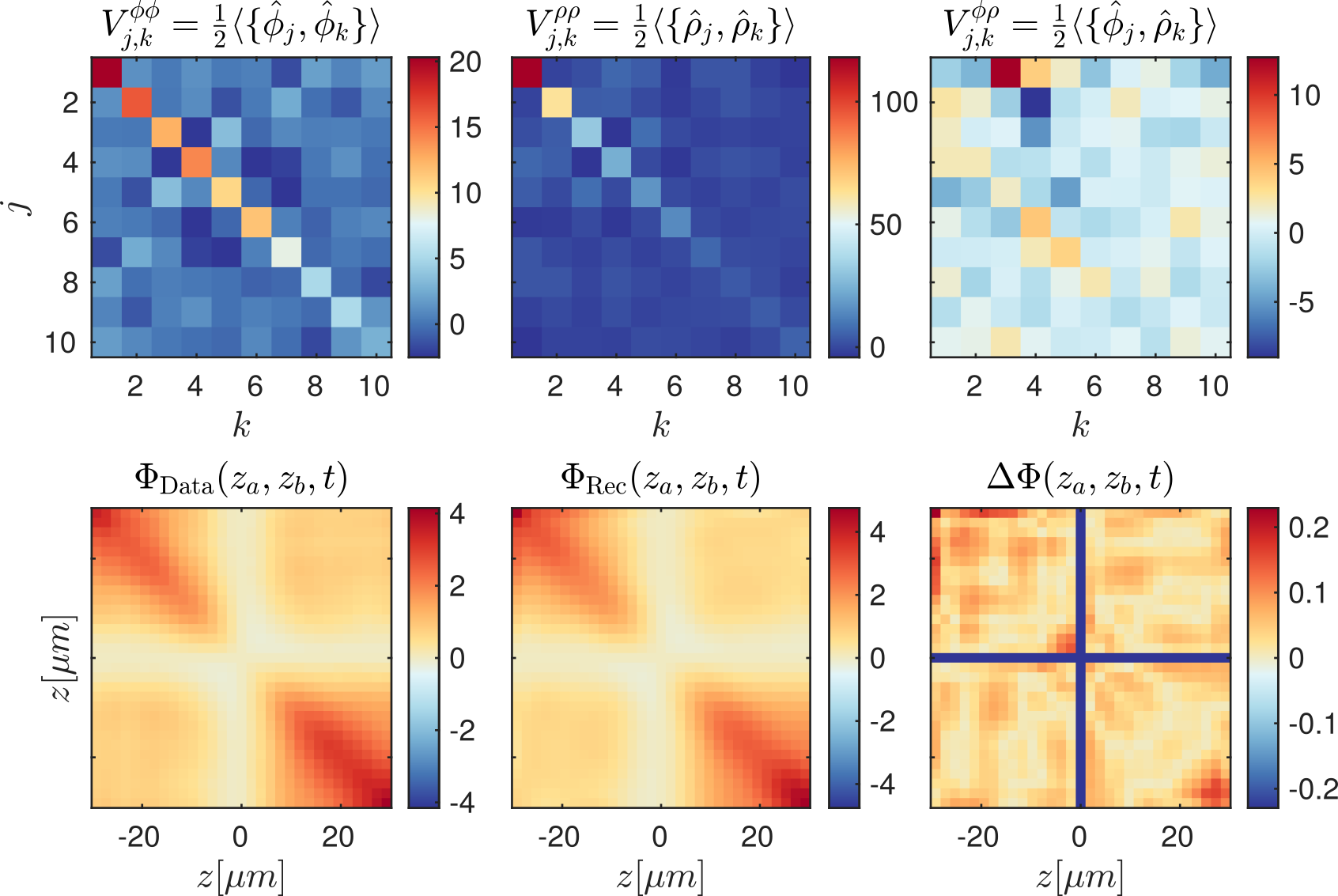
Tomography Klein-Gordon thermal state after quench
H^KG=H^TLL+J∫dznGPφ^2
\hat H_\text{KG}=\hat H_\text{TLL}+J\int \mathrm{d}z \,n_{GP} \hat \varphi^2
Data by M. Tajik, J. Schmiedmayer
Towards entanglement
Issue #1: Gibbs phenomenon
10 eigen-modes:
20 eigen-modes:
Issue #2: Zero mode missing in tomography
H^TLL=∑k>02ℏωk(ϕk2+δρ^k2)+gρ^02
\hat H_\text{TLL} = \sum_{k>0} \frac {\hbar \omega_k}2 (\phi_k^2+\delta\hat\rho_k^2) + g\hat\rho_0^2
⟨ϕ^02(t)⟩=⟨ϕ^02(0)⟩+g2t2⟨δρ^02(0)⟩
\langle\hat \phi_0^2(t)\rangle= \langle\hat \phi_0^2(0)\rangle +g^2t^2 \langle \delta\hat \rho_0^2(0)\rangle
Towards entanglement
Role of the zero mode in entanglement
Squeezing criterion needs:
ϕ^L+ϕ^R=ϕ^0=∫dzφ^(z)
\hat\phi_L+ \hat\phi_R = \hat\phi_0 = \int \mathrm{d}z \hat \varphi(z)
ϕ^L=∫Ldzφ^(z)
\hat\phi_L = \int_L \mathrm{d}z \hat \varphi(z)
ϕ^R=∫Rdzφ^(z)
\hat\phi_R = \int_R \mathrm{d}z \hat \varphi(z)
ϕ^L−ϕ^R≈ϕ^1=∫dzφ^(z)cos(2πz)
\hat\phi_L- \hat\phi_R \approx \hat\phi_1 = \int \mathrm{d}z \hat \varphi(z) \cos(2\pi z)
Not available in tomography
Conclusions
The atom chip experiment in Vienna:
M. Tajik, J. Schmiedmayer
S. Sotiriadis, J. Eisert
T. Schweigler, J. Sabino, F. Cataldini, S-C. Ji, F. Moller
Exciting simplicity!
Mechanisms for the emergence of Gaussian correlations Marek Gluza presenting based on collaboration with T. Schweigler, M. Tajik, J. Sabino, F. Cataldini, S-C. Ji, F. Moller, B. Rauer, J. Schmiedmayer, J. Eisert, S. Sotiriadis https://arxiv.org/abs/2108.07829 NTU Singapore 2108.07829
Mechanisms for the emergence of Gaussian correlations
By Marek Gluza
Mechanisms for the emergence of Gaussian correlations
- 1,895
