Tomography slides for Jörg
Marek Gluza
NTU Singapore
slides.com/marekgluza
Gaussian quantum simulators
How?
Ultra-cold 1d gases
Inside: atoms
Outside: wavepackets
hydrodynamics
Energy of phonons
E
E
E
E
\hat H_\text{TLL} = \int \text{d}z\left[ \frac{\hbar^2n_{GP}}{2m}\partial_z\hat\varphi^2+g\delta\hat\varrho^2\right]
\delta\varrho
\partial_z\varphi
\partial_z\varphi
\ll
\delta\varrho
\ll
Tomonaga-Luttinger liquid
Interferometry measures velocities
van Nieuwkerk, Schmiedmayer, Essler, arXiv:1806.02626
Schumm, Schmiedmayer, Kruger, et al., arXiv:quant-ph/0507047
\partial_z\hat \varphi(z) \approx\frac{\hat \varphi(z)-\hat \varphi(z+\Delta z)}{\Delta z}
\Delta z
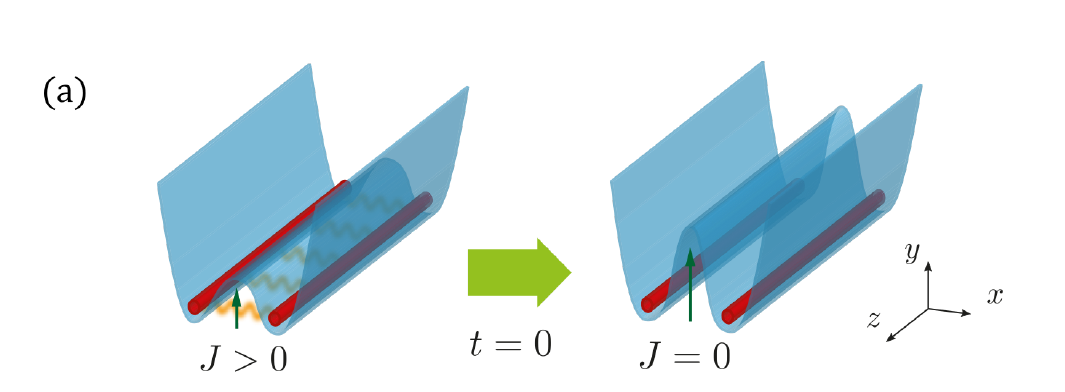
Quantum field refrigerators in the TLL model:
System
Piston
Bath
Bath with excitations
System cooled down
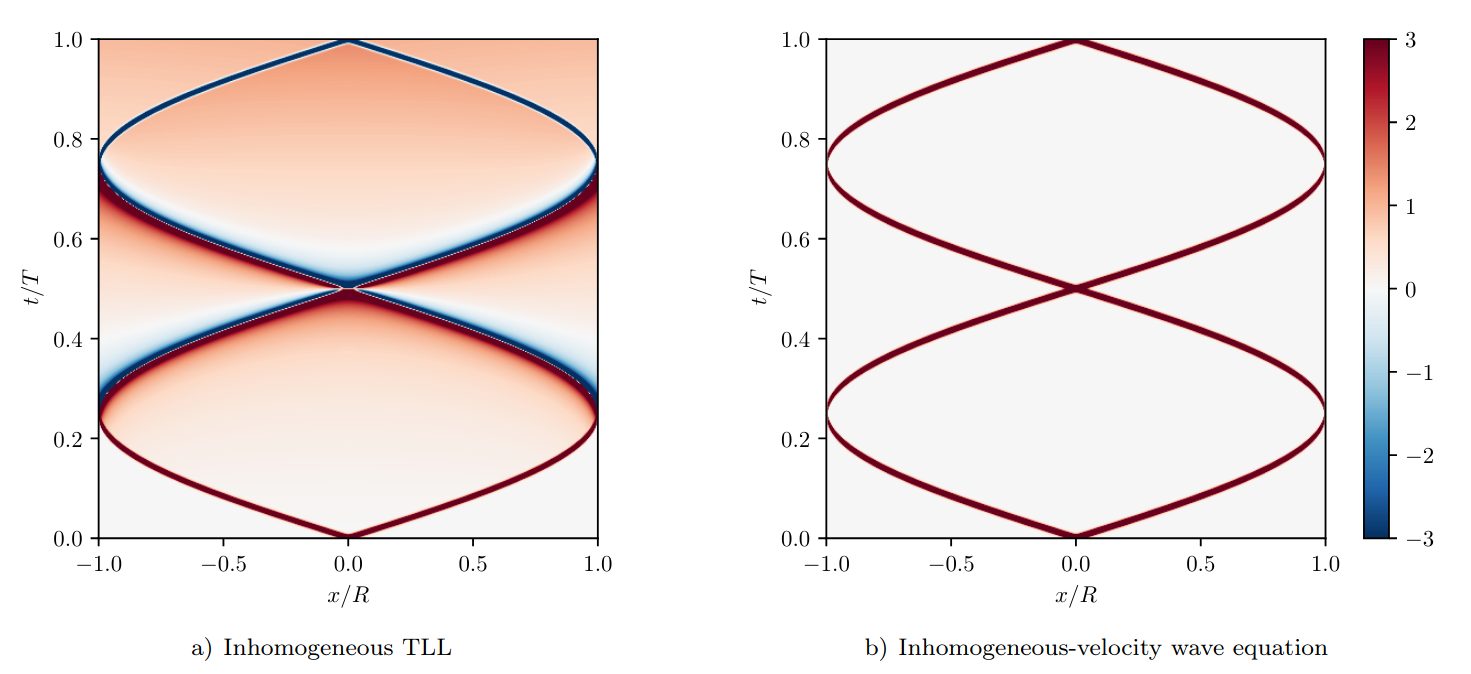
Breaking of the Huygens-Fresnel principle
in the inhomogenous TLL model:
Why?
Why develop continuous field
quantum simulators?
- Representation theory: Quantum information?
- Continuum limits: BQP and QMA or more?
- Are nanowires computationally hard to simulate?
What do we know is difficult?
SM
Fundamental
Universal
Effective
Why develop continuous field
quantum simulators?
- Representation theory: Quantum information?
- Continuum limits: BQP and QMA or more?
- Are nanowires computationally hard to simulate?
What do we know is difficult?
SM
Fundamental
Universal
Effective
Non-thermal
steady states
Sine-Gordon
thermal states
Atomtronics
Generalized hydrodynamics
Recurrences
Some highlights:
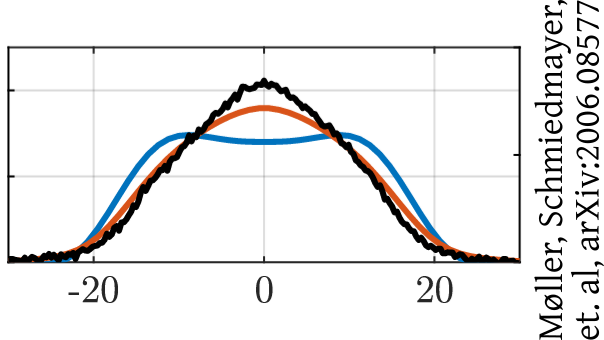
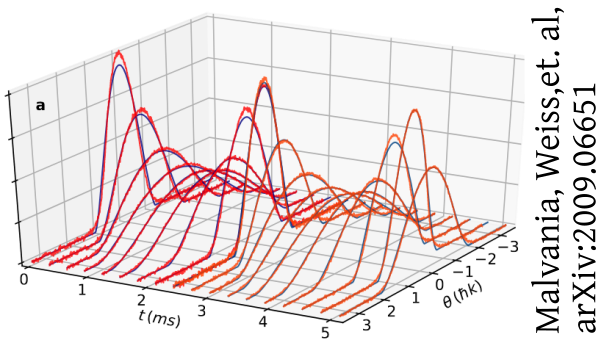
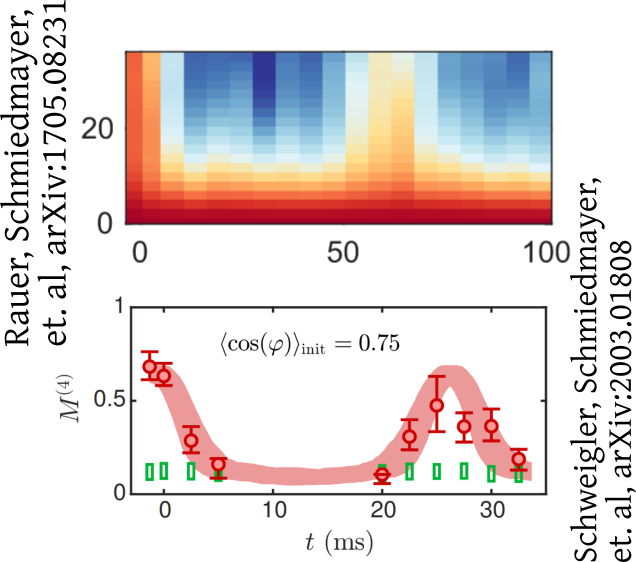
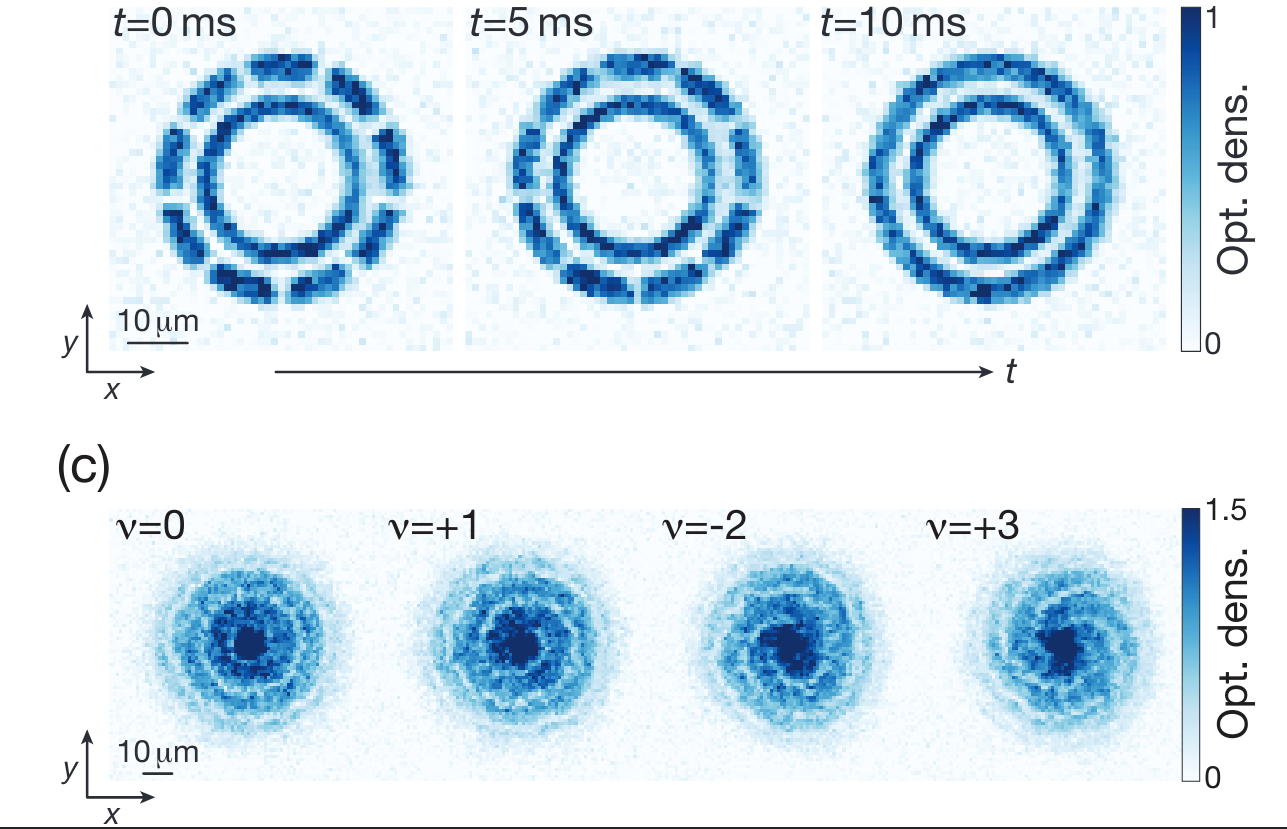
Interferometry measures velocities
van Nieuwkerk, Schmiedmayer, Essler, arXiv:1806.02626
Schumm, Schmiedmayer, Kruger, et al., arXiv:quant-ph/0507047
\partial_z\hat \varphi(z) \approx\frac{\hat \varphi(z)-\hat \varphi(z+\Delta z)}{\Delta z}
\partial_z\hat \varphi(z) \approx\frac{\Delta\hat\varphi(z)}{\Delta z}
\Delta z
Tomography
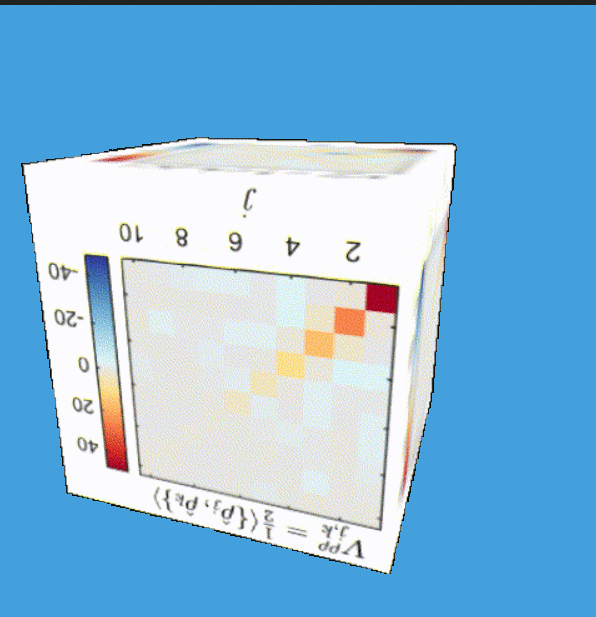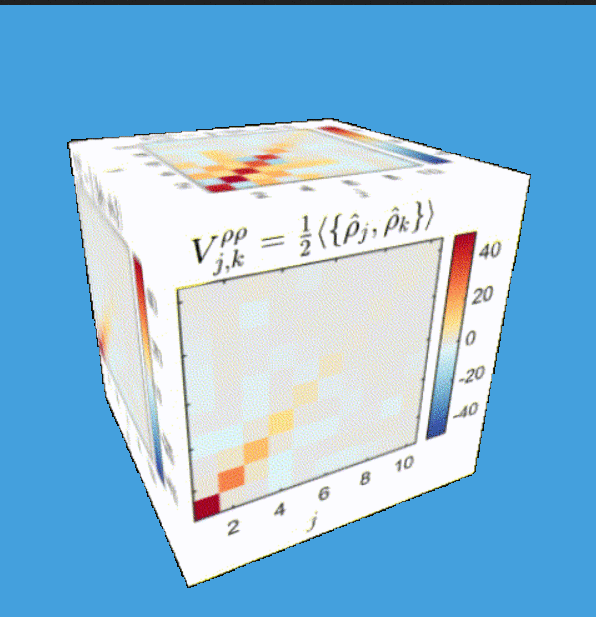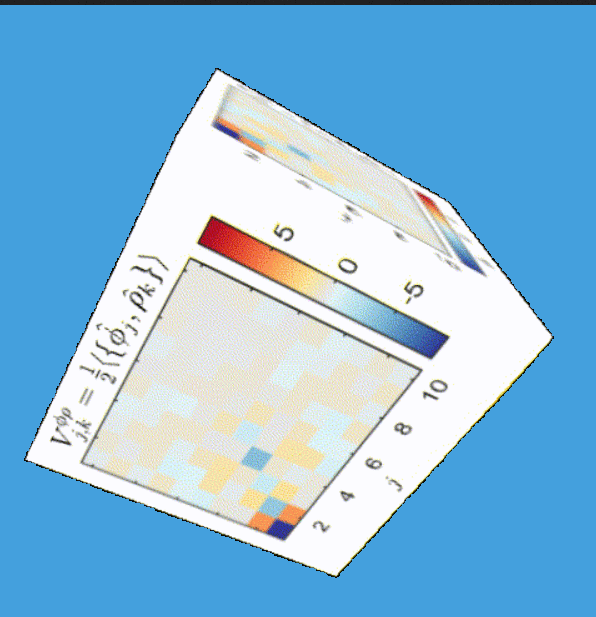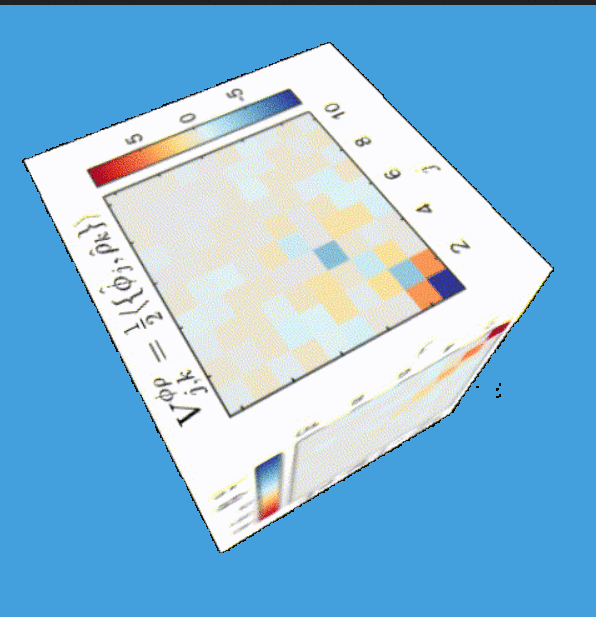
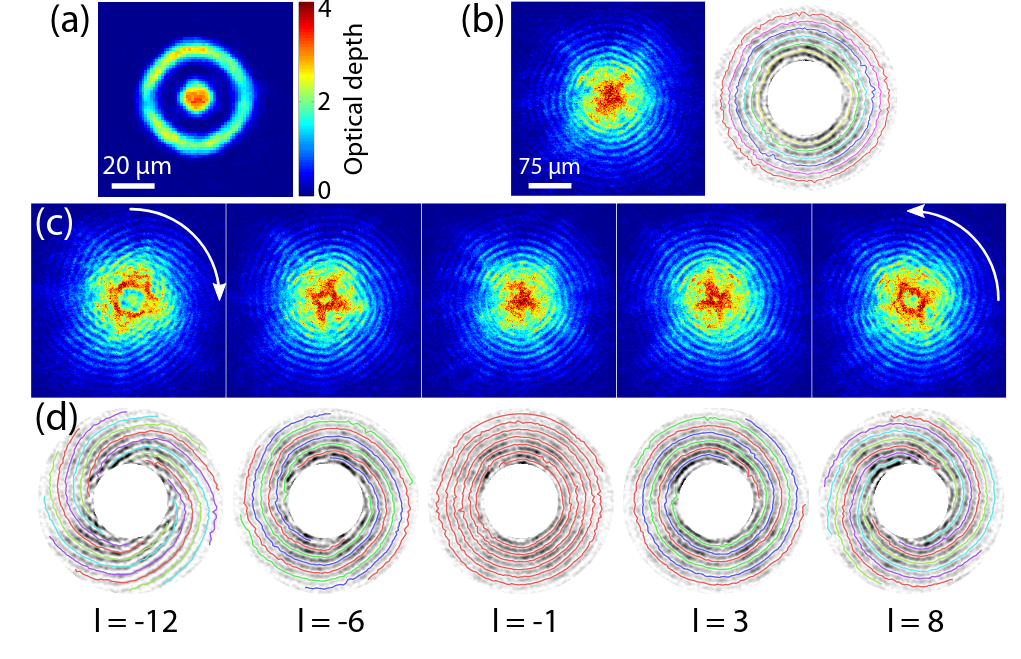
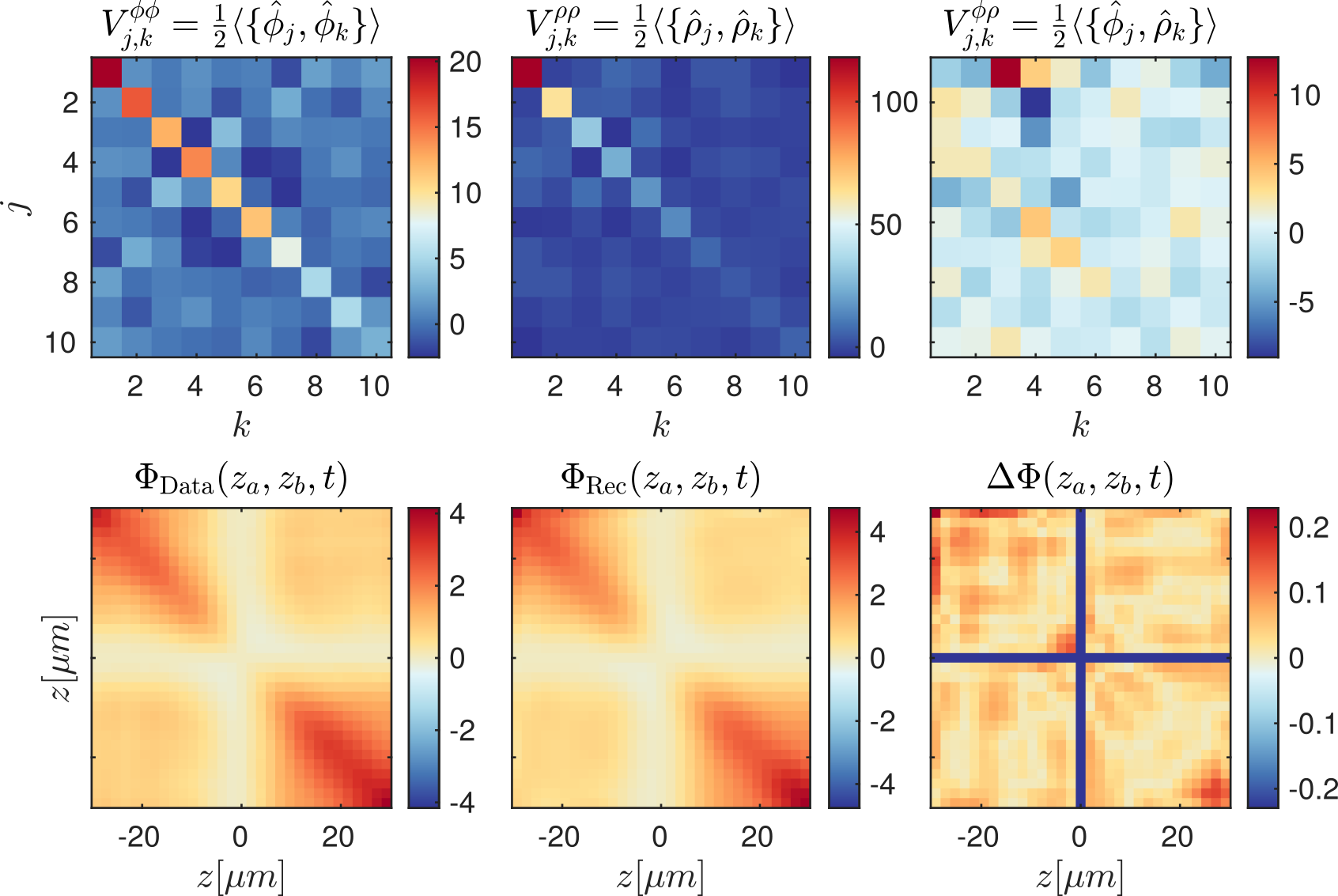
Tomography for phonons
\hat H_\text{TLL} = \int \text{d}z\left[ \frac{\hbar^2n_{GP}}{2m}\partial_z\hat\varphi^2+g\delta\hat\varrho^2\right]
\hat H_\text{TLL} = \sum_{k>0} \frac {\hbar \omega_k}2 (\phi_k^2+\delta\hat\rho_k^2) + g\hat\rho_0^2
\langle\hat \phi_k^2(t)\rangle= \cos^2(\omega_k t) \langle \phi_k^2(0)\rangle \\
\quad\quad\quad\quad\quad+\sin^2(\omega_k t) \langle \delta\hat \rho_k^2(0)\rangle
\delta \hat\rho
\langle\hat \phi^2(t)\rangle
\langle\delta\hat \rho^2(0)\rangle =0?
\langle \hat \phi^2(0)\rangle
\hat \phi
Tomography for phonons
\hat H_\text{TLL} = \int \text{d}z\left[ \frac{\hbar^2n_{GP}}{2m}\partial_z\hat\varphi^2+g\delta\hat\varrho^2\right]
\hat H_\text{TLL} = \sum_{k>0} \frac {\hbar \omega_k}2 (\phi_k^2+\delta\hat\rho_k^2) + g\hat\rho_0^2
\langle\hat \phi_k^2(t)\rangle= \cos^2(\omega_k t) \langle \phi_k^2(0)\rangle \\
\quad\quad\quad\quad\quad+\sin^2(\omega_k t) \langle \delta\hat \rho_k^2(0)\rangle
\delta \hat\rho
\langle\hat \phi^2(t)\rangle
\langle\delta\hat \rho^2(0)\rangle =0?
\langle \hat \phi^2(0)\rangle
\hat \phi
What are eigenmodes?
\hat H_\text{TLL} = \int \text{d}z\left[ \frac{\hbar^2n_{GP}}{2m}\partial_z\hat\varphi^2+g\delta\hat\varrho^2\right]
\hat H_\text{TLL} = \sum_{k>0} \frac {\hbar \omega_k}2 (\phi_k^2+\delta\hat\rho_k^2) + g\hat\rho_0^2
\hat \phi_k = \int_0^L dz \cos(\pi k z/L)\hat \varphi(z)
\int_0^L dz \cos(\pi k z/L)\cos(\pi k'z/L) = \delta_{k,k'}
Transmutation
\langle\hat \phi_k^2(t)\rangle= \cos^2(\omega_k t) \langle \hat\phi_k^2(0)\rangle +\sin^2(\omega_k t) \langle \delta\hat \rho_k^2(0)\rangle
\langle\hat \phi_k^2(t)\rangle= \langle \hat\phi_k^2(0)\rangle
\langle\hat \phi_k^2(t)\rangle= \langle \delta\hat \rho_k^2(0)\rangle
t=0:
t=\frac{\pi}{2\omega_k}:
\delta \hat\rho
\langle\hat \phi^2(t)\rangle
\langle\delta\hat \rho^2(0)\rangle =0?
\langle \hat \phi^2(0)\rangle
\hat \phi
Tomography
A_{1,2}= \sin^2(\omega_k t_1 )
A_{1,1}= \cos^2(\omega_k t_1)
\langle\hat \phi_k^2(t)\rangle= \cos^2(\omega_k t) \langle \hat\phi_k^2(0)\rangle+ \sin^2(\omega_k t) \langle \delta\hat \rho_k^2(0)\rangle
A_{3,2}= \sin^2(\omega_k t_3 )
A_{3,1}= \cos^2(\omega_k t_3)
A_{2,2}= \sin^2(\omega_k t_2 )
A_{2,1}= \cos^2(\omega_k t_2)
A
\begin{pmatrix} \langle \hat\phi_k^2(0)\rangle \\\langle \delta\hat \rho_k^2(0)\rangle
\end{pmatrix}
=\begin{pmatrix} \langle \hat\phi_k^2(t_1)\rangle \\\langle \hat\phi_k^2(t_2)\rangle \\\langle \hat\phi_k^2(t_3)\rangle \end{pmatrix}
\|Aq - d\| = \text{min}
(This formalism: Tomography for many modes)
Tomography Klein-Gordon thermal state after quench
\hat H_\text{KG}=\hat H_\text{TLL}+J\int \mathrm{d}z \,n_{GP} \hat \varphi^2
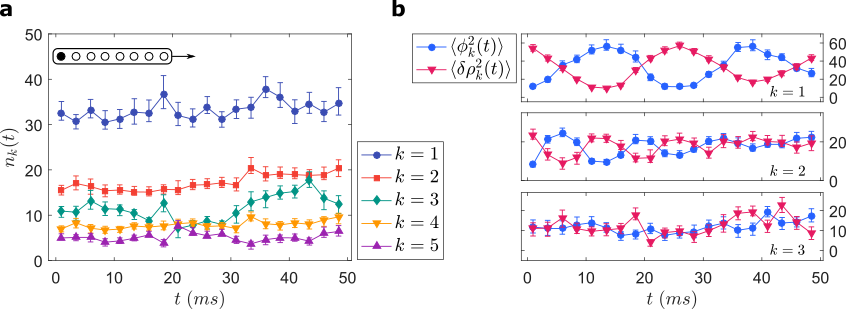
Extracting physical properties
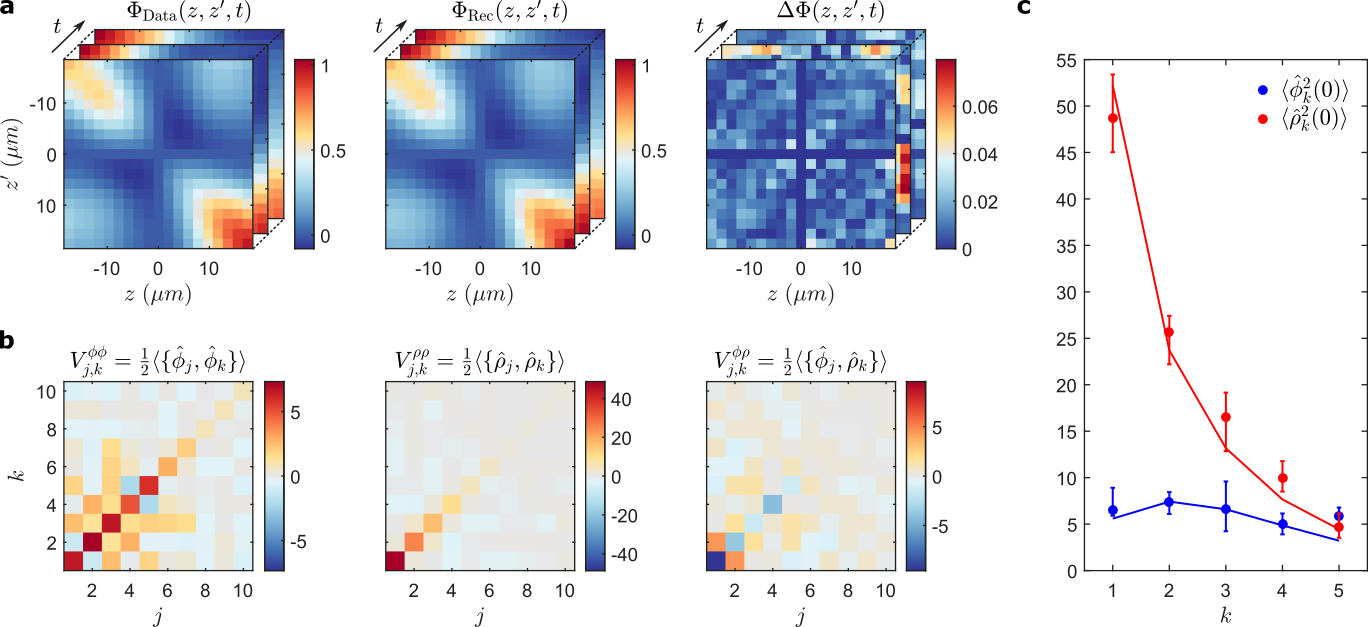
Extracting physical properties
Extracting physical properties
Tomography for optical lattices
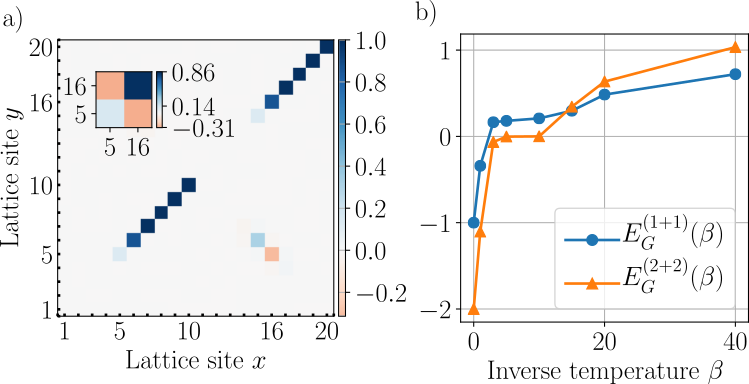
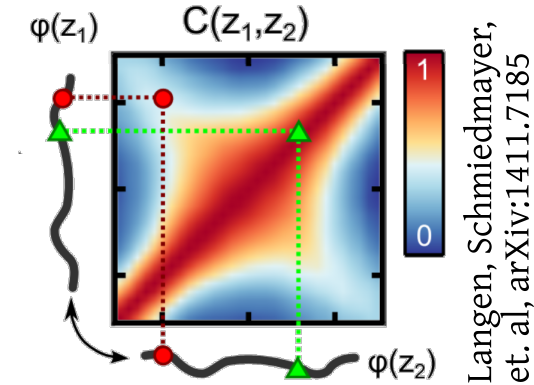
What about quantum correlations?
Tomography Klein-Gordon thermal state after quench
\hat H_\text{KG}=\hat H_\text{TLL}+J\int \mathrm{d}z \,n_{GP} \hat \varphi^2
Data by M. Tajik, J. Schmiedmayer
Towards entanglement
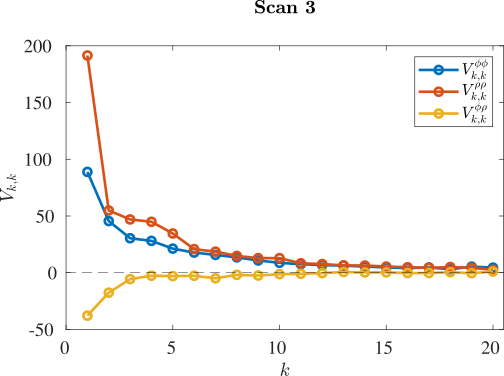
Issue #1: Gibbs phenomenon
10 eigen-modes:
20 eigen-modes:
Issue #2: Zero mode missing in tomography
\hat H_\text{TLL} = \sum_{k>0} \frac {\hbar \omega_k}2 (\phi_k^2+\delta\hat\rho_k^2) + g\hat\rho_0^2
\langle\hat \phi_0^2(t)\rangle= \langle\hat \phi_0^2(0)\rangle +g^2t^2 \langle \delta\hat \rho_0^2(0)\rangle
Towards entanglement
Role of the zero mode in entanglement
Squeezing criterion needs:
\hat\phi_L+ \hat\phi_R = \hat\phi_0 = \int \mathrm{d}z \hat \varphi(z)
\hat\phi_L = \int_L \mathrm{d}z \hat \varphi(z)
\hat\phi_R = \int_R \mathrm{d}z \hat \varphi(z)
\hat\phi_L- \hat\phi_R \approx \hat\phi_1 = \int \mathrm{d}z \hat \varphi(z) \cos(2\pi z)
Not available in tomography
What?
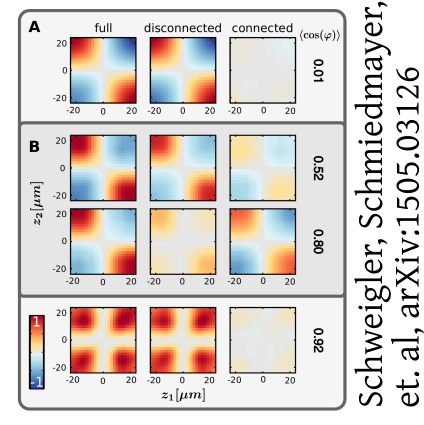
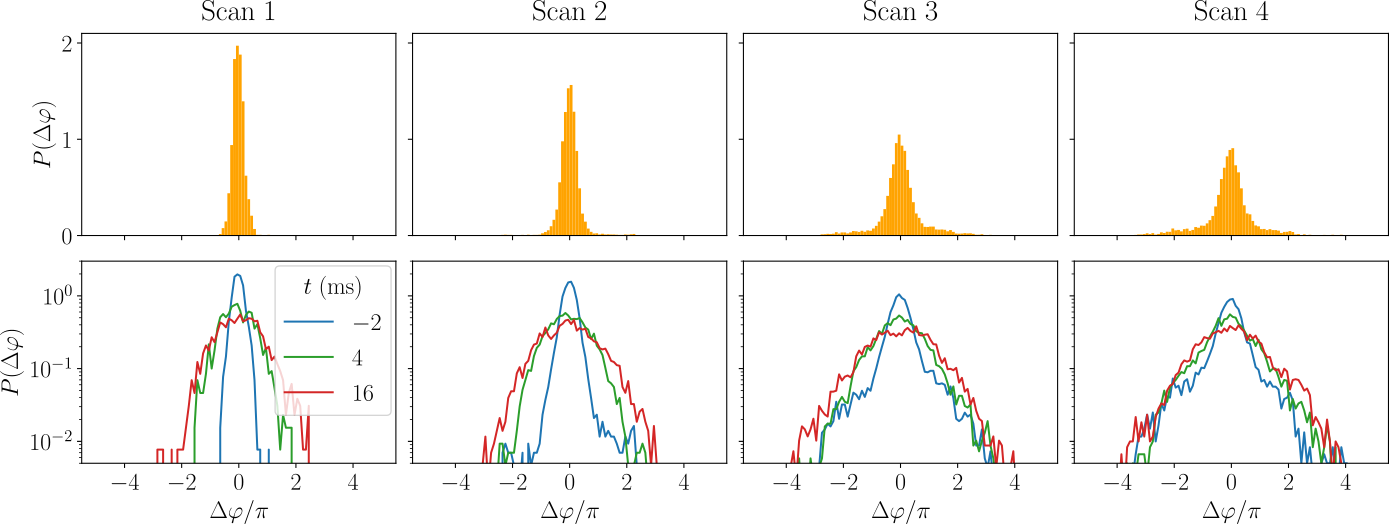
What about correlations?
z
z'
\langle \Delta\hat\varphi(z)\Delta\hat\varphi(z')\rangle/ \Delta z^2 \approx \langle \partial_z\hat\varphi(z)\partial_z\hat\varphi(z')\rangle
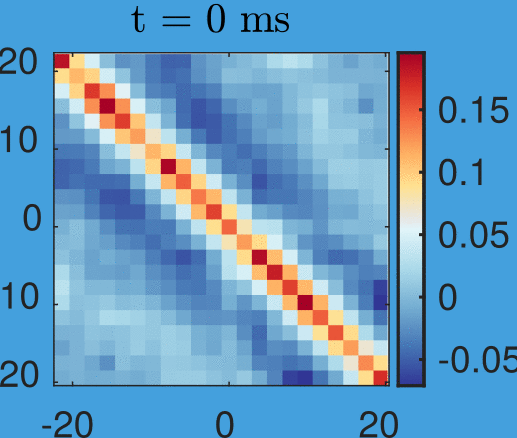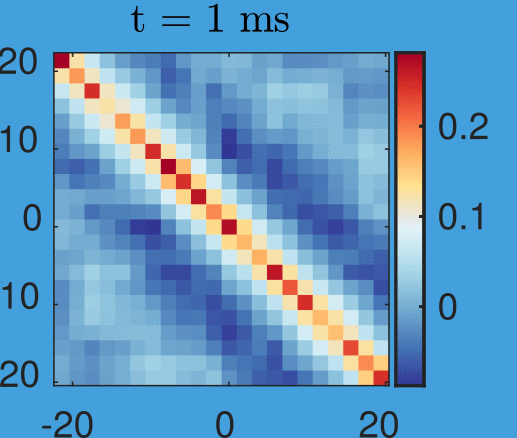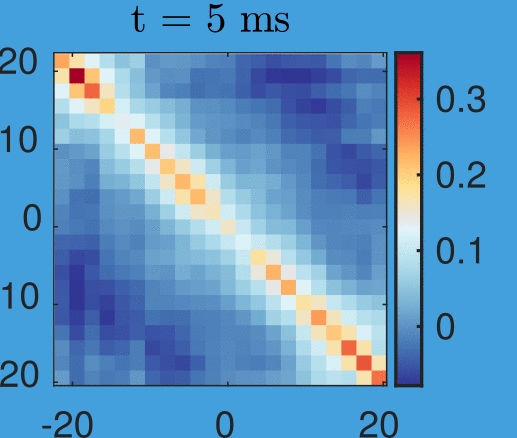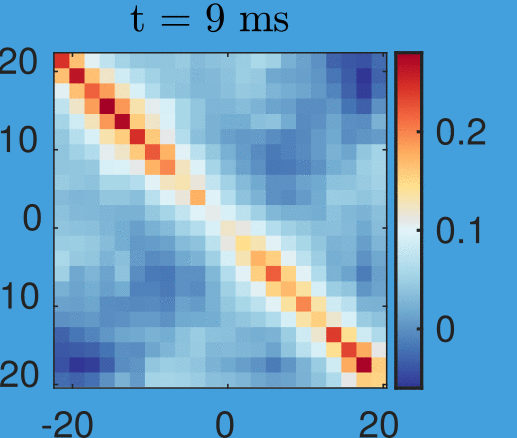
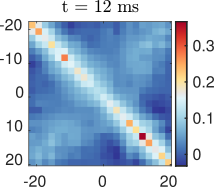
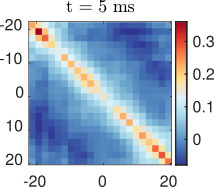
Velocity correlations:
Velocity correlations
z
z'
C(z,z') \approx \frac{\langle \Delta\hat\varphi(z)\Delta\hat\varphi(z')\rangle}{ \Delta z^2 }
\langle \Delta\hat\varphi(z)\Delta\hat\varphi(z')\rangle/ \Delta z^2 <0
Anti-correlation:
Left moves opposite to right
z
z'
And with anti-correlation:
C(z,z') \approx \frac{\langle \Delta\hat\varphi(z)\Delta\hat\varphi(z')\rangle}{ \Delta z^2 }
C(z,z',t) \approx \frac{\langle \Delta\hat\varphi(z,t)\Delta\hat\varphi(z',t)\rangle}{ \Delta z^2 }
New data by M. Tajik, J. Schmiedmayer
Time step: 1ms
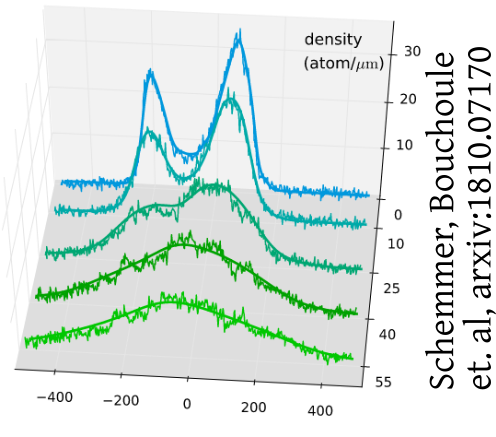
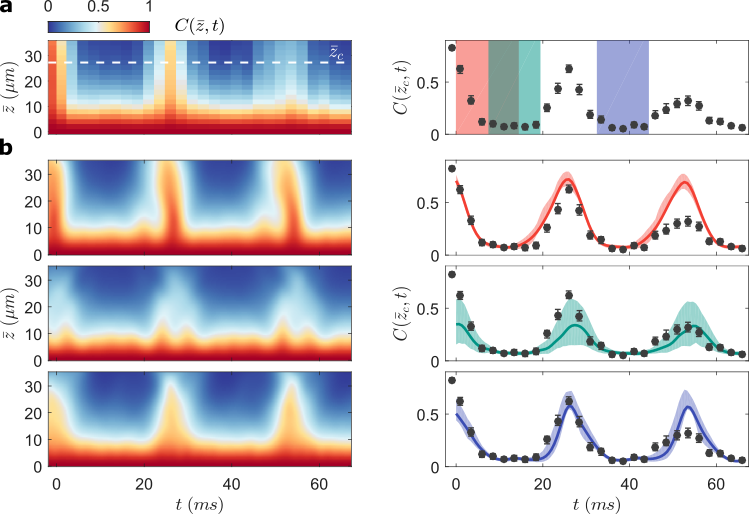
Simplicity arising from a quench:
Data by M. Tajik, J. Schmiedmayer
Mechanisms for the emergence of Gaussian correlations
Marek Gluza
presenting based on collaboration with
T. Schweigler, M. Tajik, J. Sabino, F. Cataldini, S-C. Ji, F. Moller, B. Rauer, J. Schmiedmayer, J. Eisert, S. Sotiriadis
NTU Singapore
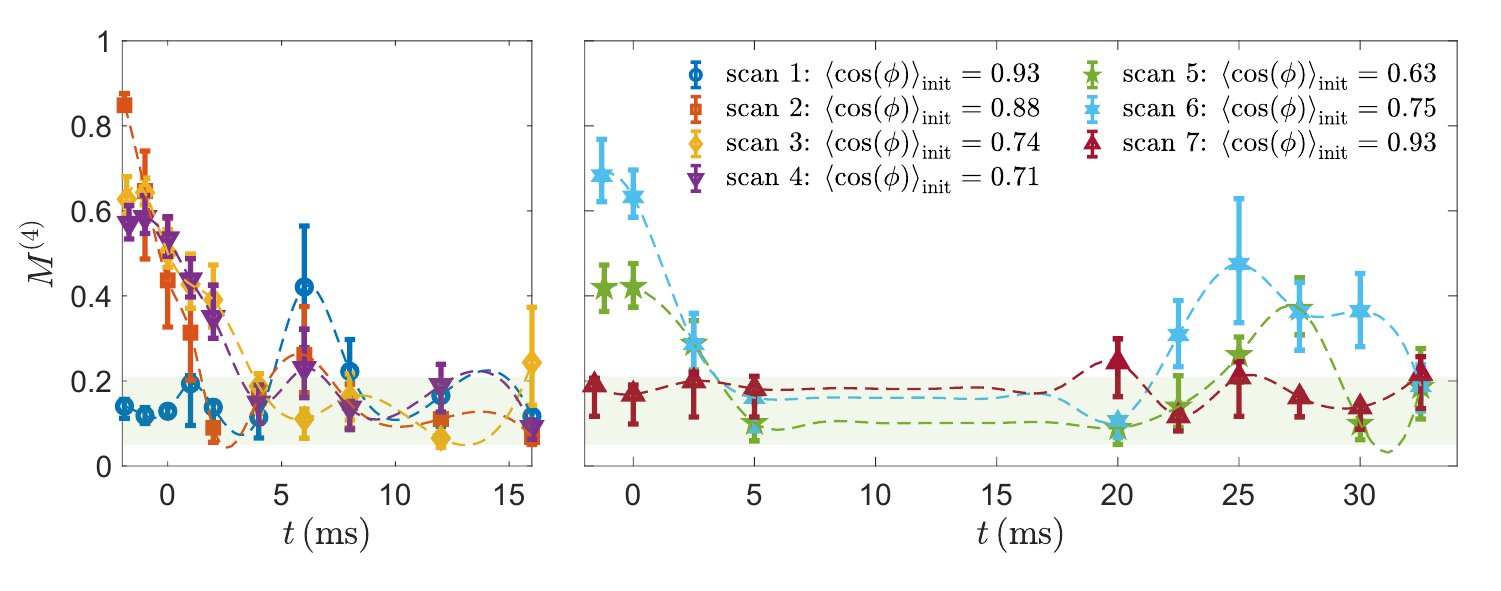
Initial non-Gaussianity decays
Why does it decay?
The system is isolated
Initial non-Gaussianity decays
Why does it revive?
The system is isolated
Then it revives
Phase fluctuations
Phase derivative correlations
increase with distance
decay but sizeable
Effective light cone
not dispersive
Tomonaga-Luttinger liquid
Inhomogeneous
Breaking of Huygens-Fresnel principle in inhomogeneous Tomonaga-Luttinger liquids
Huygens-Fresnel principle
\hat H_\text{TLL}
= \int_{0}^{L} \mathrm{d}x\,v_\text{S}
\biggl(
K \partial_{x} \hat{\phi}(x)^2
+ {K}^{-1}\partial_{t} \hat{\phi}(x)^2
\biggr)
Tomonaga-Luttinger liquid
Tomonaga-Luttinger liquid
Cold atoms as
an inhomogeneous
\hat H_\text{TLL} = \int_0^L \text{d}x\biggl( \frac{\hbar^2n_{GP}}{2m}\partial_x\hat\varphi^2+g\delta\hat\varrho^2\biggr)
\delta\varrho
\partial_z\varphi
\partial_z\varphi
\ll
\delta\varrho
\ll
\hat H_\text{TLL}
= \int_{0}^{L} \mathrm{d}x\,v_\text{S}
\biggl(
K \partial_{x} \hat{\phi}(x)^2
+ {K}^{-1}\partial_{t} \hat{\phi}(x)^2
\biggr)
\hat H
= \int_{0}^{L} \mathrm{d}x\,v(x)
\biggl(
{K(x)}^{-1} \hat\pi (x)^2
+ K(x) \partial_{x} \hat{\phi}(x)^2
\biggr)
n_\text{GP}(x)
{K(x)}
v(x)
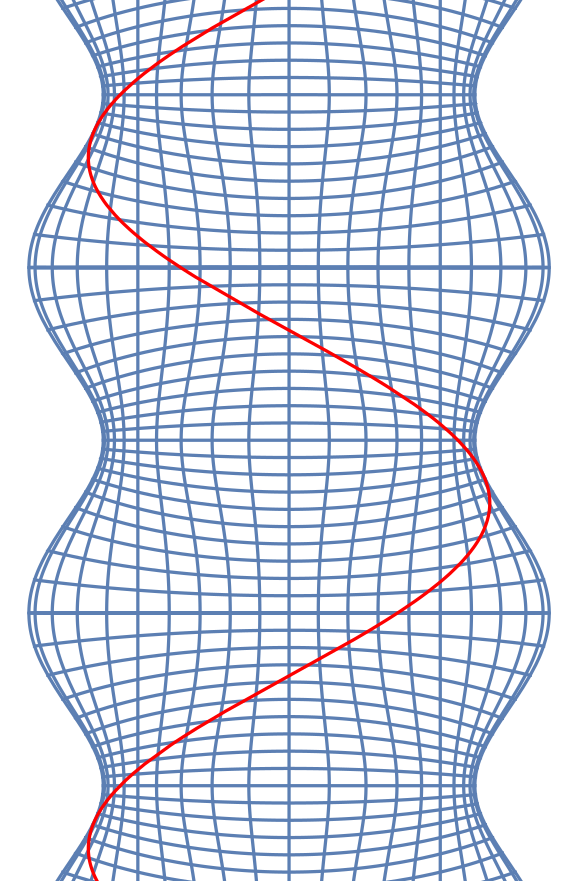
Huygens-Fresnel principle
Huygens-Fresnel principle broken
\partial_{t}^{2} \hat{\phi}
= 2 v(x) v'(x) \partial_{x} \hat{\phi}
+ v(x)^2 \partial^2_{x} \hat{\phi}
\partial_{t}^{2} \hat{\phi}
= v(x)v'(x) \partial_{x} \hat{\phi}
+ v(x)^2\partial^2_{x} \hat{\phi}
\mapsto
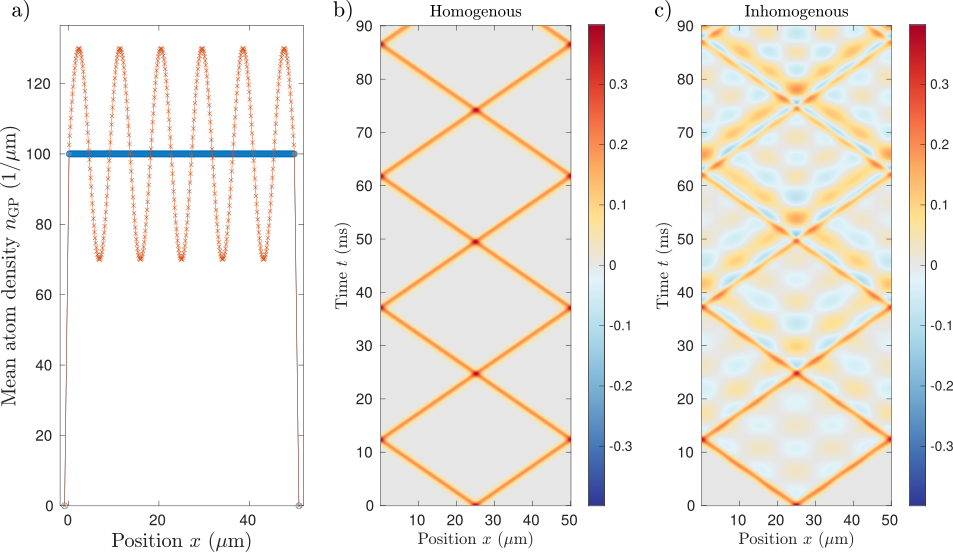
The factor 2 is the source of leakage into the light-cone
Breaking of Huygens-Fresnel principle in inhomogeneous Tomonaga-Luttinger liquids
Marek Gluza
Spyros Sotiriadis
Per Moosavi
\partial_{t}^{2} \hat{\phi}
= 2 v(x) v'(x) \partial_{x} \hat{\phi}
+ v(x)^2 \partial^2_{x} \hat{\phi}
\partial_{t}^{2} \hat{\phi}
= v(x)v'(x) \partial_{x} \hat{\phi}
+ v(x)^2\partial^2_{x} \hat{\phi}
\mapsto
NTU Singapore
Tomography overview
By Marek Gluza
