Tomography
and non-equilibrium dynamics
in continuous field quantum simulators
Marek Gluza
Experiment
Theory
presenting based on new data by M. Tajik, J. Schmiedmayer
S. Sotiriadis, J. Eisert
T. Schweigler, J. Sabino, F. Cataldini, S-C. Ji, F. Moller
Simplicity
in continuous field quantum simulators
Simplicity
new data by M. Tajik, J. Schmiedmayer
S. Sotiriadis
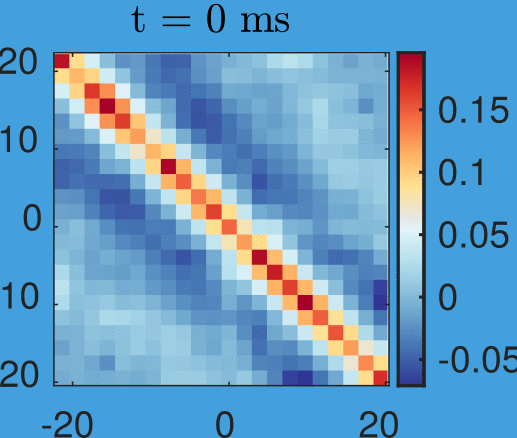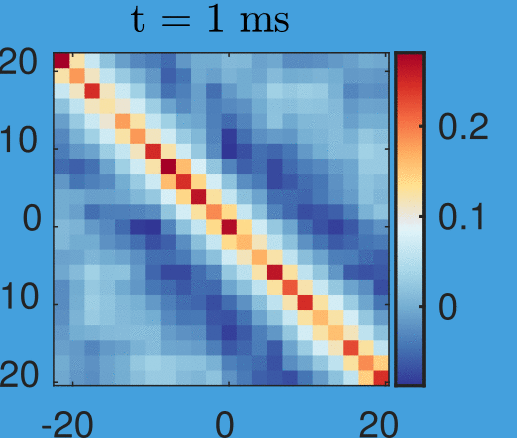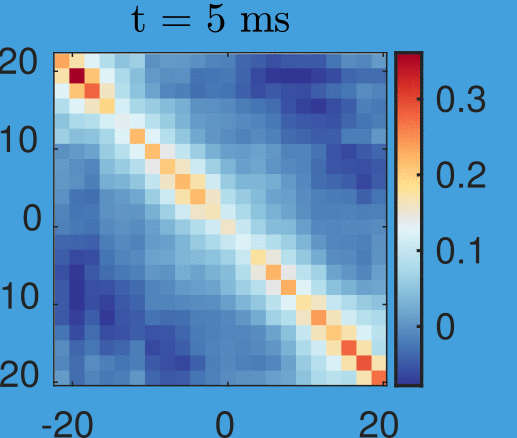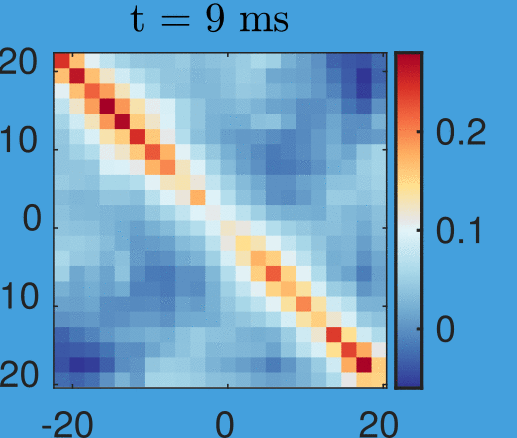
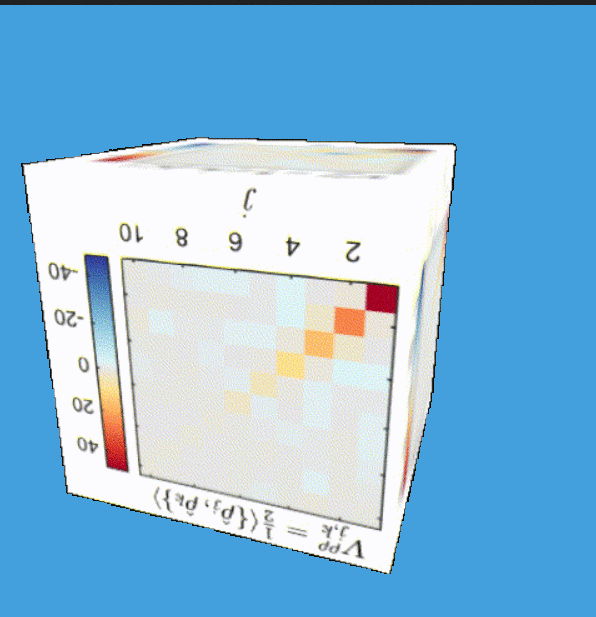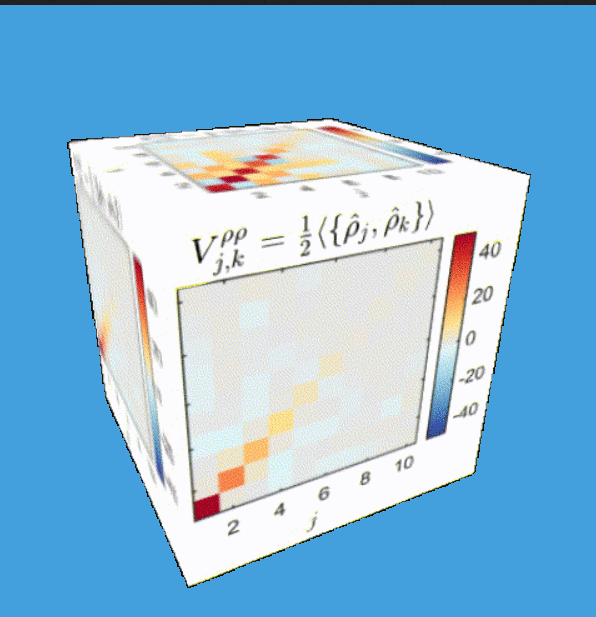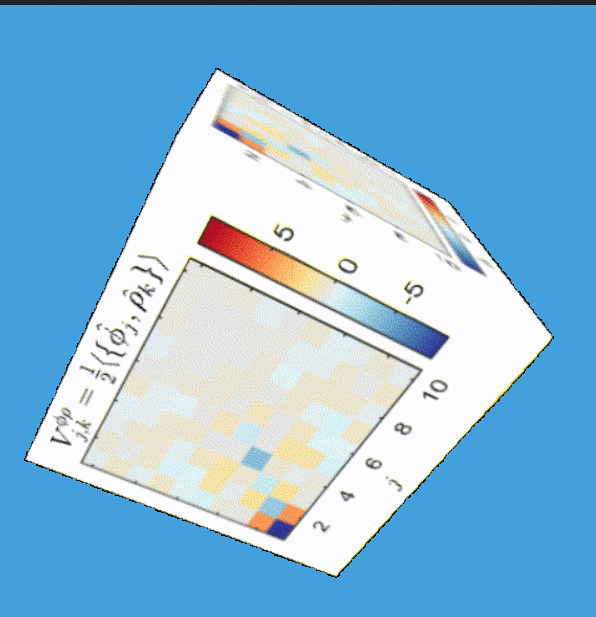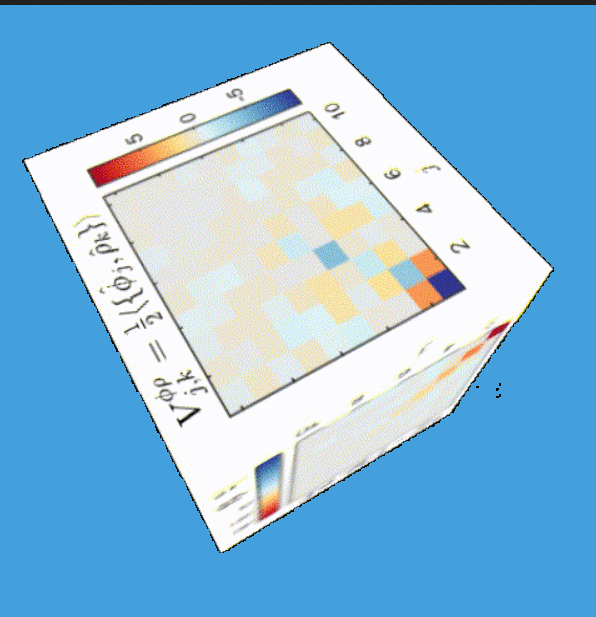
Based on new data by M. Tajik, J. Schmiedmayer
Simplicity
from a quench
How?
1d gases
Inside: atoms
Outside: wavepackets
hydrodynamics
Energy of phonons
E
E
E
E
\hat H_\text{TLL} = \int \text{d}z\left[ \frac{\hbar^2n_{GP}}{2m}\partial_z\hat\varphi^2+g\delta\hat\varrho^2\right]
\delta\varrho
\partial_z\varphi
\partial_z\varphi
\ll
\delta\varrho
\ll
Tomonaga-Luttinger liquid
Gluza&Sabino&Vitaliagno&Ng, Huber&Schmiedmayer&Eisert, arixv:2006.01177
Quantum field refrigerators in the TLL model:
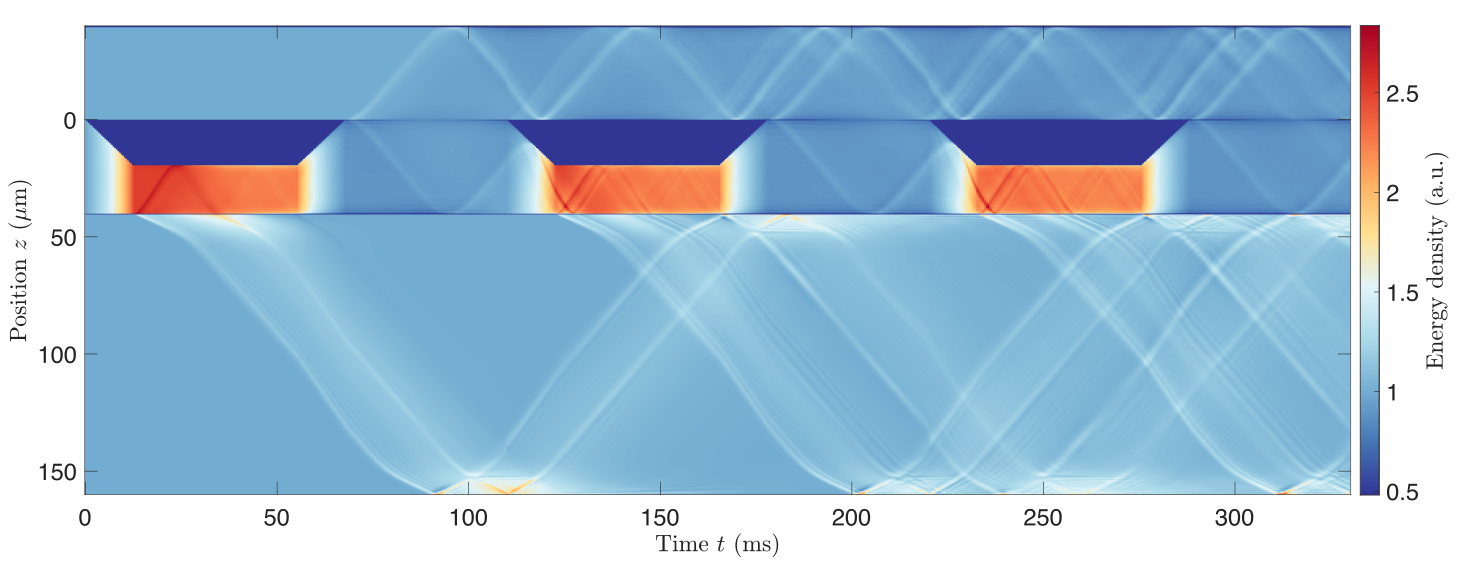
System
Piston
Bath
Bath with excitations
System cooled down
Breaking of the Huygens-Fresnel principle
in the inhomogenous TLL model:
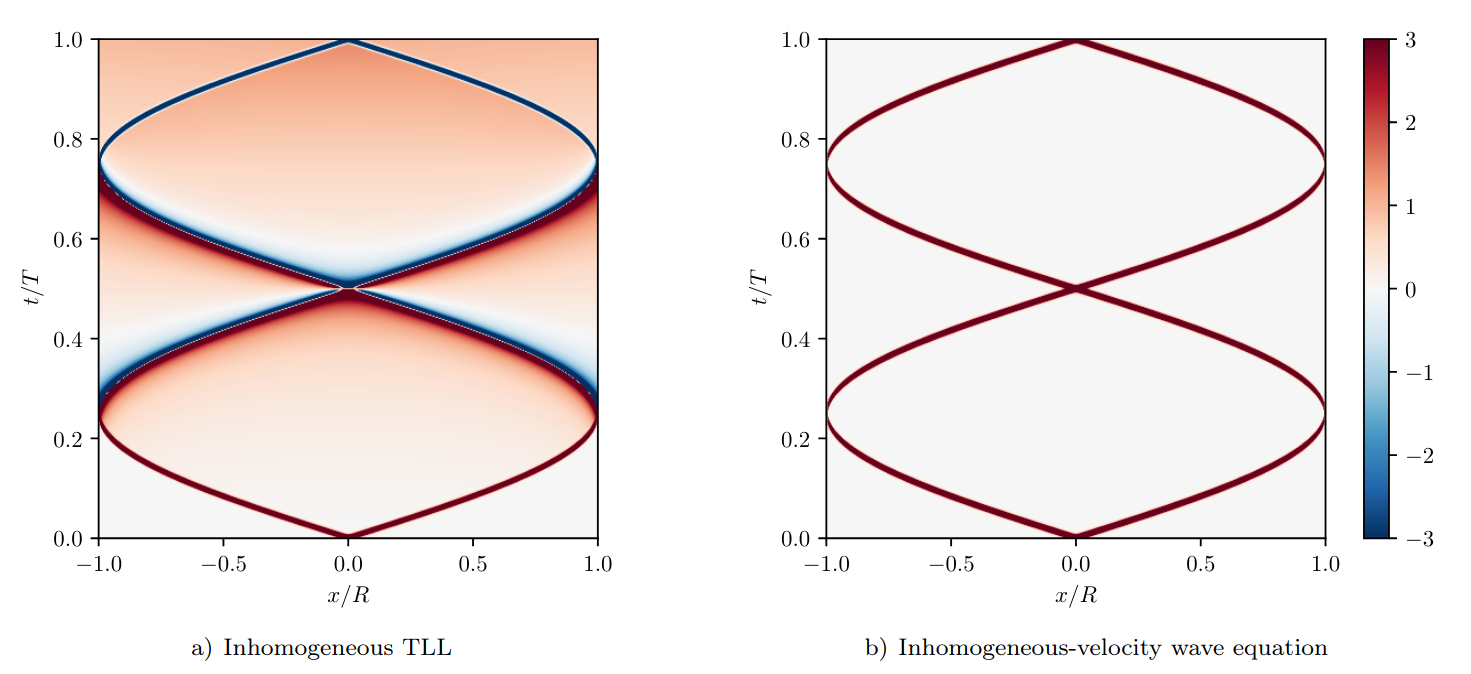
Gluza, Moosavi, Sotiriadis, arxiv:2104.07751
Why?
Why develop continuous field
quantum simulators?
- Representation theory: Quantum information?
- Continuum limits: BQP and QMA or more?
- Are nanowires computationally hard to simulate?
What do we know is difficult?
SM
Fundamental
Universal
Effective
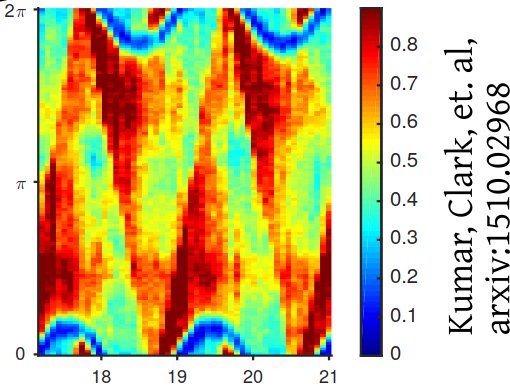
Non-thermal
steady states
Sine-Gordon
thermal states
Atomtronics
Generalized hydrodynamics
Recurrences
Some highlights:
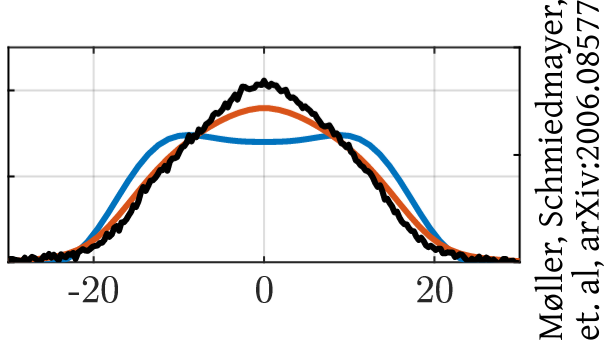
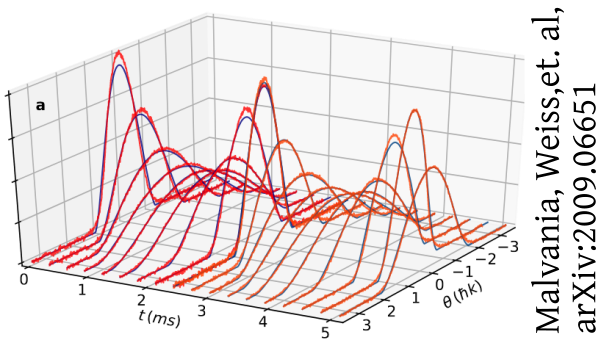
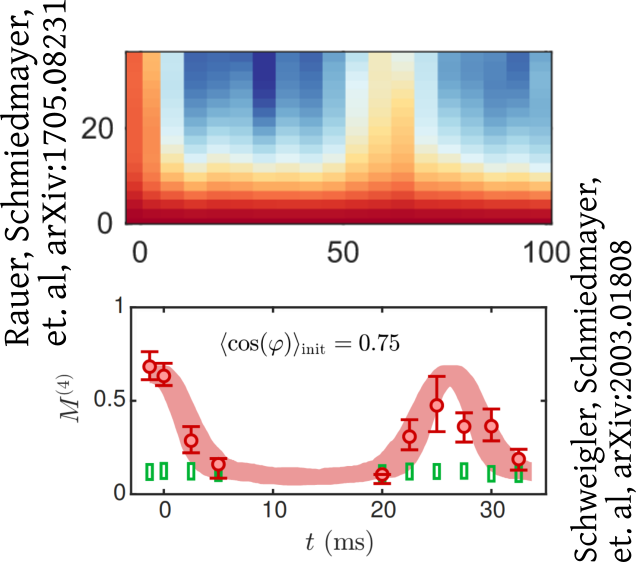
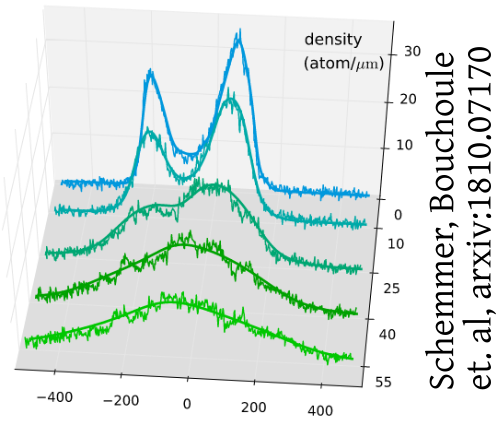
Interferometry measures velocities
van Nieuwkerk, Schmiedmayer, Essler, arXiv:1806.02626
Schumm, Schmiedmayer, Kruger, et al., arXiv:quant-ph/0507047
\partial_z\hat \varphi(z) \approx\frac{\hat \varphi(z)-\hat \varphi(z+\Delta z)}{\Delta z}
\partial_z\hat \varphi(z) \approx\frac{\Delta\hat\varphi(z)}{\Delta z}
\Delta z
What?
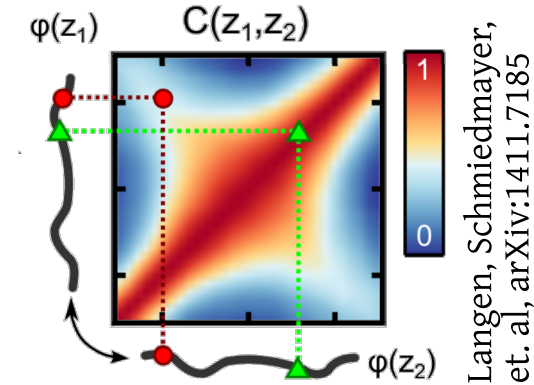
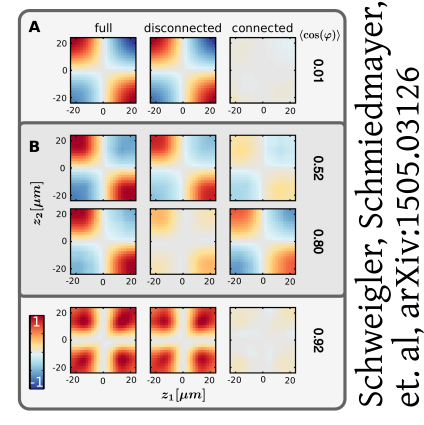
What about correlations?
z
z'
\langle \Delta\hat\varphi(z)\Delta\hat\varphi(z')\rangle/ \Delta z^2 \approx \langle \partial_z\hat\varphi(z)\partial_z\hat\varphi(z')\rangle
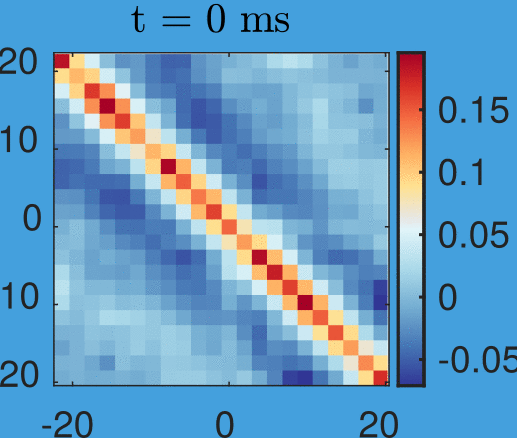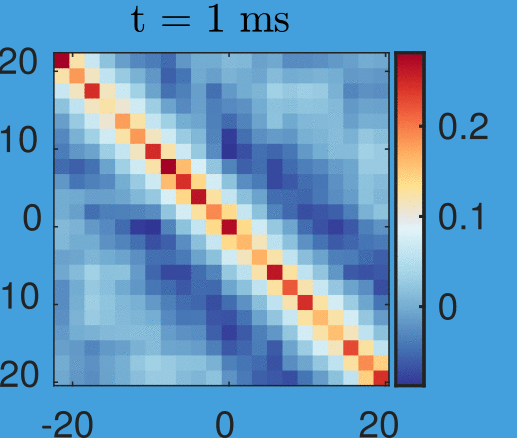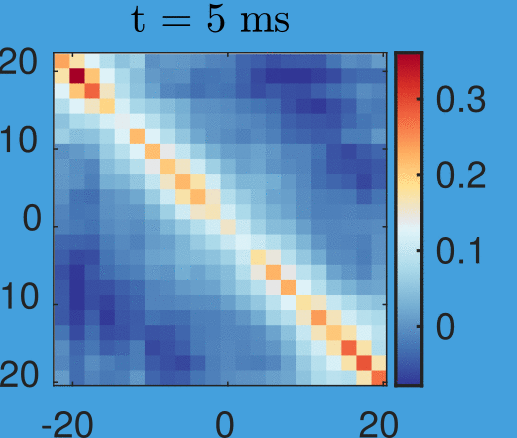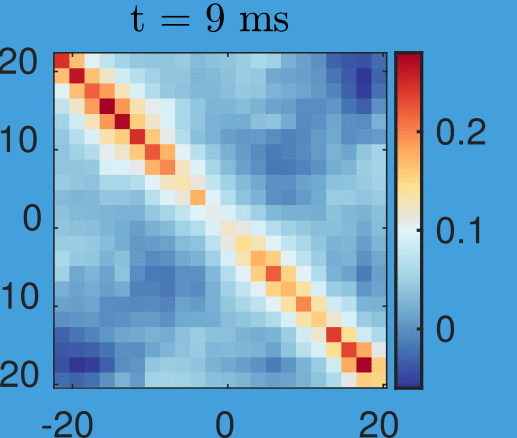
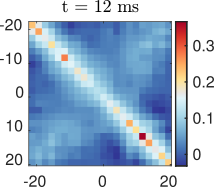
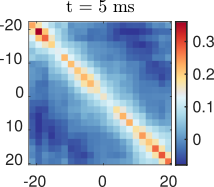
Velocity correlations:
\langle \Delta\hat\varphi(z)\Delta\hat\varphi(z')\rangle/ \Delta z^2 <0
Anti-correlation:
Left moves opposite to right
z
z'
Velocity correlations
z
z'
C(z,z') \approx \frac{\langle \Delta\hat\varphi(z)\Delta\hat\varphi(z')\rangle}{ \Delta z^2 }
And with anti-correlation:
C(z,z') \approx \frac{\langle \Delta\hat\varphi(z)\Delta\hat\varphi(z')\rangle}{ \Delta z^2 }
C(z,z',t) \approx \frac{\langle \Delta\hat\varphi(z,t)\Delta\hat\varphi(z',t)\rangle}{ \Delta z^2 }
New data by M. Tajik, J. Schmiedmayer
Time step: 1ms
Simplicity arising from a quench:
Data by M. Tajik, J. Schmiedmayer
What?
What about quantum correlations?
Tomography for phonons
\hat H_\text{TLL} = \int \text{d}z\left[ \frac{\hbar^2n_{GP}}{2m}\partial_z\hat\varphi^2+g\delta\hat\varrho^2\right]
\hat H_\text{TLL} = \sum_{k>0} \frac {\hbar \omega_k}2 (\phi_k^2+\delta\hat\rho_k^2) + g\rho_0^2
\langle\hat \phi_k^2(t)\rangle= \cos^2(\omega_k t) \langle \phi_k^2(0)\rangle \\
\quad\quad\quad\quad\quad+\sin^2(\omega_k t) \langle \delta\hat \rho_k^2(0)\rangle
\delta \hat\rho
\langle\hat \phi^2(t)\rangle
\langle\delta\hat \rho^2(0)\rangle =0?
\langle \hat \phi^2(0)\rangle
\hat \phi
Gluza, Schmiedmayer&Eisert, et al, arxiv:1807.04567
Gluza, Eisert, arxiv:2005.09000
Tomography Klein-Gordon thermal state after quench
\hat H_\text{KG}=\hat H_\text{TLL}+J\int \mathrm{d}z \,n_{GP} \hat \varphi^2
Data by M. Tajik, J. Schmiedmayer
Towards entanglement
Issue #1: Gibbs phenomenon
10 eigen-modes:
20 eigen-modes:
Issue #2: Zero mode missing in tomography
\hat H_\text{TLL} = \sum_{k>0} \frac {\hbar \omega_k}2 (\phi_k^2+\delta\hat\rho_k^2) + g\hat\rho_0^2
\langle\hat \phi_0^2(t)\rangle= \langle\hat \phi_0^2(0)\rangle +g^2t^2 \langle \delta\hat \rho_0^2(0)\rangle
Towards entanglement
Role of the zero mode in entanglement
Squeezing criterion needs:
\hat\phi_L+ \hat\phi_R = \hat\phi_0 = \int \mathrm{d}z \hat \varphi(z)
\hat\phi_L = \int_L \mathrm{d}z \hat \varphi(z)
\hat\phi_R = \int_R \mathrm{d}z \hat \varphi(z)
\hat\phi_L- \hat\phi_R \approx \hat\phi_1 = \int \mathrm{d}z \hat \varphi(z) \cos(2\pi z)
Not available in tomography
Conclusions
The atom chip experiment in Vienna:
M. Tajik, J. Schmiedmayer
S. Sotiriadis, J. Eisert
T. Schweigler, J. Sabino, F. Cataldini, S-C. Ji, F. Moller
Exciting simplicity!
Tomography and non-equilibrium dynamics in continuous field quantum simulators (Entanglement in quantum fields Heidelberg 2021)
By Marek Gluza
