Storage Engines and Data Structures

Log

Imagine a key-value store.

We'll use a simple file to append records to it and to read records from it.

Append doesn't check if a record with the same value already exists - it just appends to the end.

37, { "name": "Dhruv", "nickname": [ "The Winner" ] }

28, { "name": "Andrey", "nickname": [ "Cappadonna" ] }

28, { "name": "Andrey", "nickname": [ "Ol' Dirty Bastard" ] }

 

1st problem: performance

Set record: O(1)

Get record: O(N)

 

Index

additional metadata on the side, which acts as a signpost and helps you to locate the data you want

 

If you want to search the same data in several different ways, you may need several different indexes on different parts of the data

 

slows down writes (because has to be updated every time write occurs), but if implemented right speeds up reads

 

that's the reason DB engines don't create indexes for everything. It's up to app devs to decide which indexes to use

Hash Indexes

Relevant to key-value stores.

Let's have a hash table in memory which value is a byte offset inside the log file.

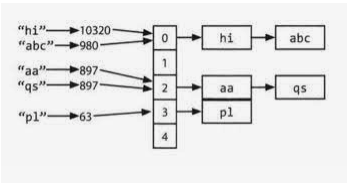
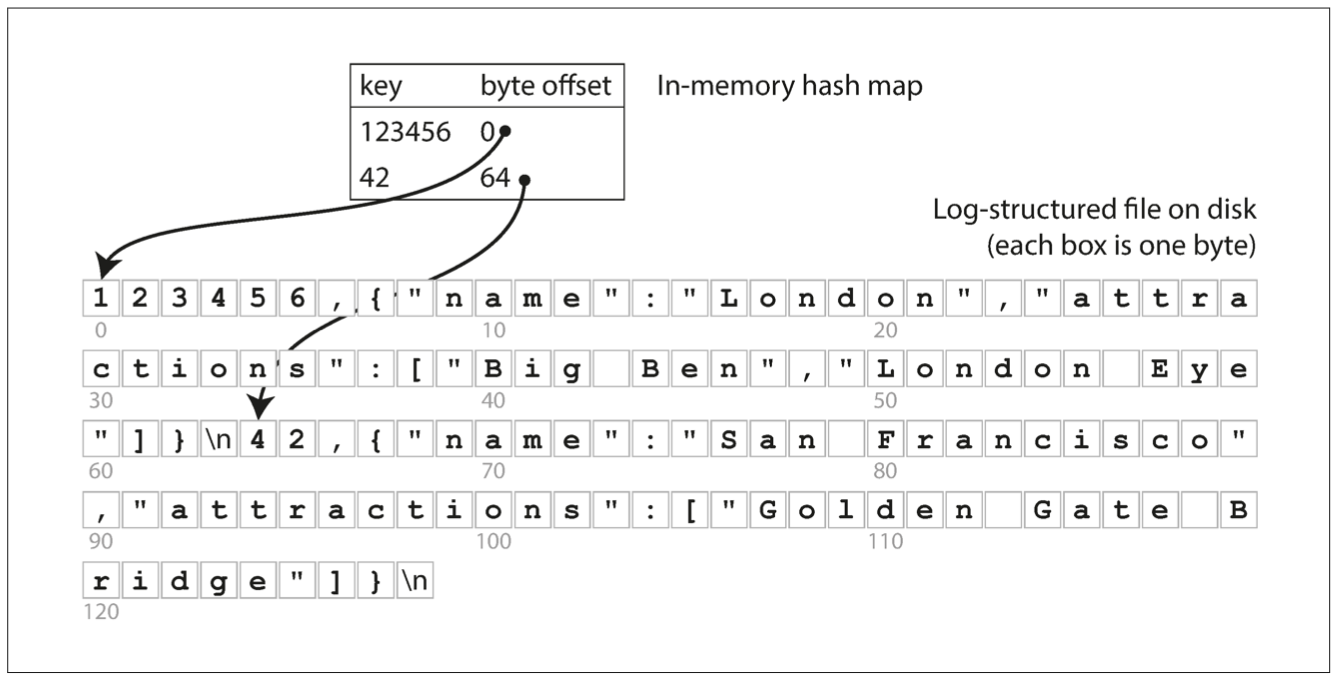
all keys must fit in the available RAM.

values can use more space since they can be loaded from a disk with just one disk seek or even from the filesystem cache

(such approach is used in Bitcask which is a default engine in Riak key-value store)

example, the key might be the URL of a cat video, and the value might be the number of times it has been played

Segments Compaction and Merging

2nd Problem: disk storage limitations

since we only append to the log but do not delete it will grow infinitely

solution: break the log into segments of specific size by closing a segment file when it reaches a particular size, and making subsequent writes to a new segment file

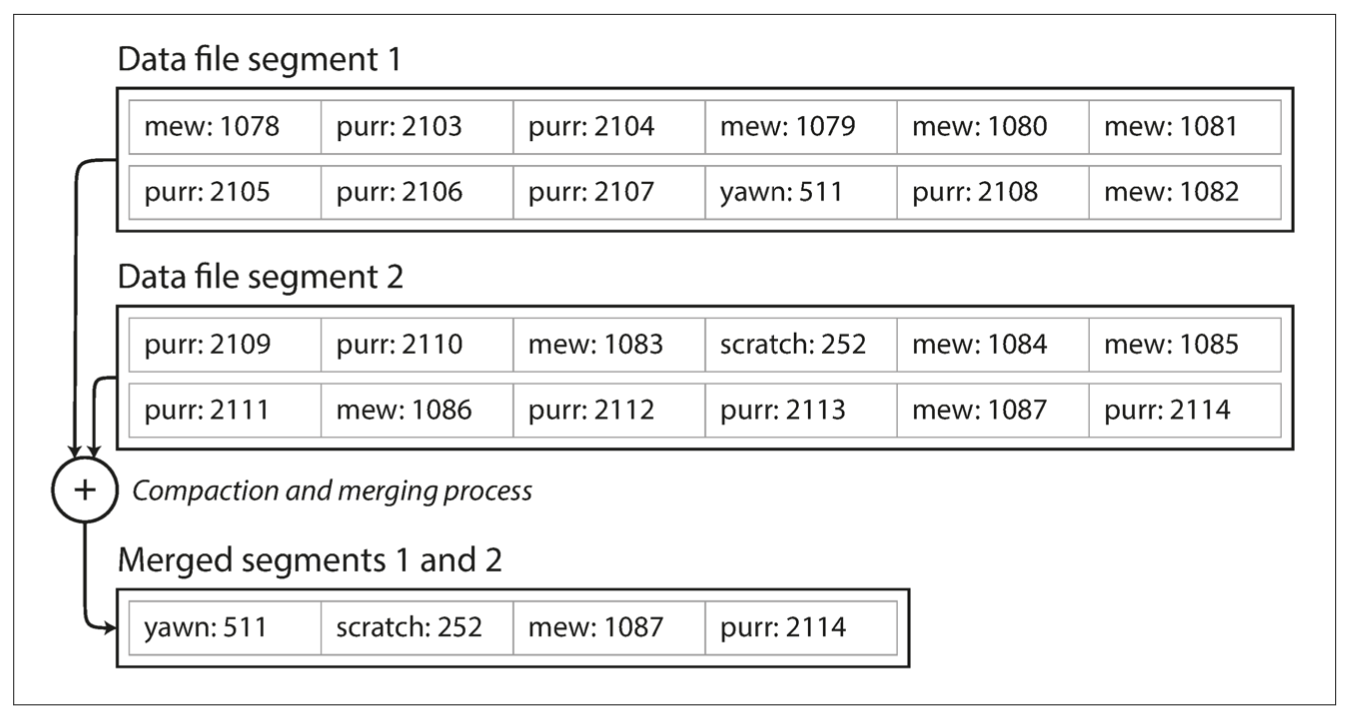
compaction - removing duplicate values within a segment

Segments Compaction and Merging

merging - compose a segment made of smaller ones.

Do together with compaction by creating a new file without interrupting reads from old frozen segments. Writes are also processed since we don't touch the last segment. After merging switch to the new file and delete old ones.

Segments Compaction and Merging

Each segment now has its own in-memory hash table, mapping keys to file offsets.

In order to find the value for a key, we first check the most recent segment’s hash map; if the key is not present we check the second-most-recent segment, and so on.

The merging process keeps the number of segments small, so lookups don’t need to check many hash maps.

Miscellaneous

File format: more storage-efficient formats can be used (binary)

 

Delete records: a special log record (tombstone). Can be executed during compaction

 

Crash recovery: dump hash maps from RAM to persistent storage to increase recovery speed (otherwise have to read the whole log to rebuild the hash map)

 

Partially written records: use checksum to remove corrupted records

 

Concurrency control: writes should be single-threaded; reads can be concurrent

Append-only vs Overwrite

Pros:

appending  (as well as segment merging) is sequential operation -> faster than random writes both on HDD (especially HDD) and SSD

crash recovery with appending is easier since the old value is not corrupted in case of partial write

merging prevents file system aging (fragmentation)

 

​Cons of hash table index approach:

a hash map should be small enough to fit in the memory

range queries are not efficient since data is not sorted - you have to look up each key individually

 

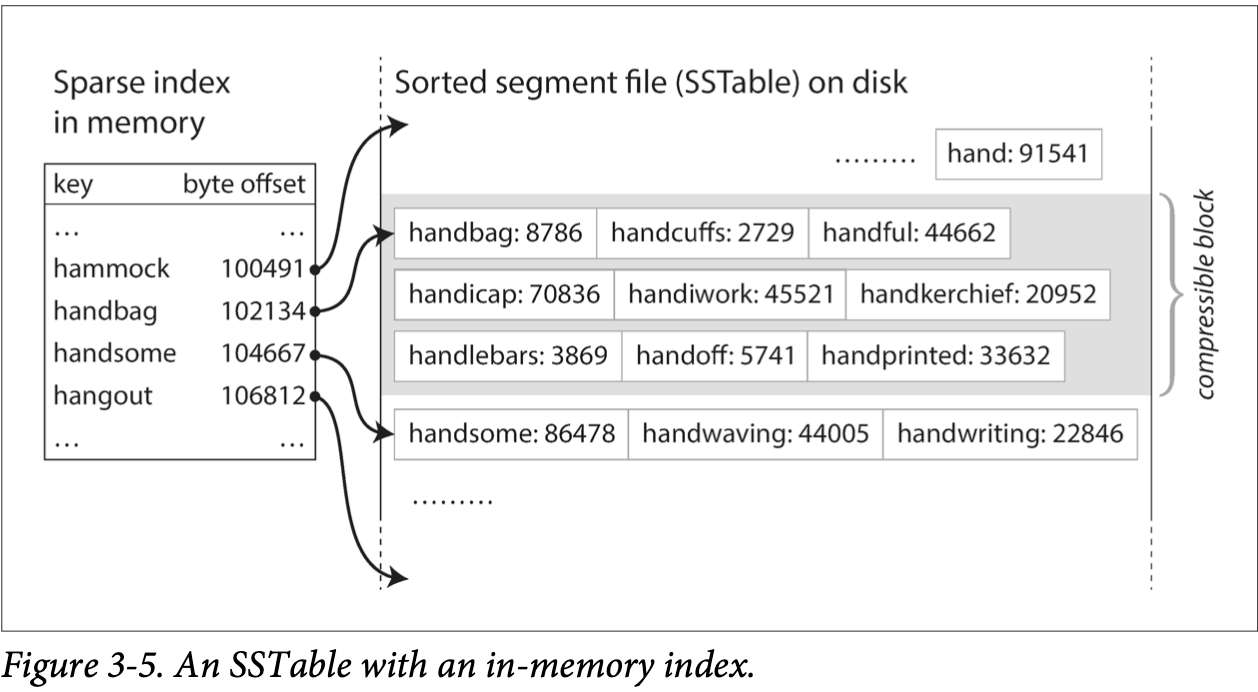
Sorted String Table (SST) - READ

records are sorted by key within a segment

segments merging is done by mergesort

hashmap can be sparse (or even we can use binary search if all records same size)

each block for key in hashmap can be compressed

 

Sorted String Table (SST) - WRITE

When a write comes in, add it to an in-memory balanced tree data structure (for example, a red-black tree). This in-memory tree is sometimes called a memtable.

 

When the memtable gets bigger than some threshold write it out to disk as a segment

 

While the SSTable is being written out to disk, writes can continue to a new memtable instance.

 

read request - first, try to find the key in the memtable, then in the most recent on-disk segment, then in the next-older segment, etc.

 

Problem: if the database crashes, the most recent writes (which are in the memtable but not yet written out to disk) are lost. Keep a parallel non-sorted log with append-only writes for that purpose. remove log every time memtable is flushed out to disk as a segment.

 

SSTables were introduced in Google’s Bigtable paper (which introduced the terms SSTable and memtable). Another name for this is Log-Structured Merge-Tree (LSM)

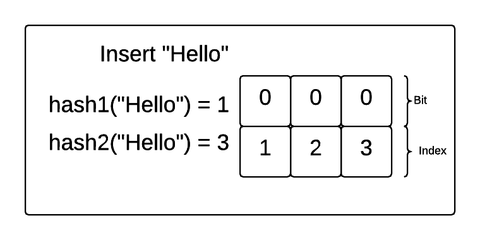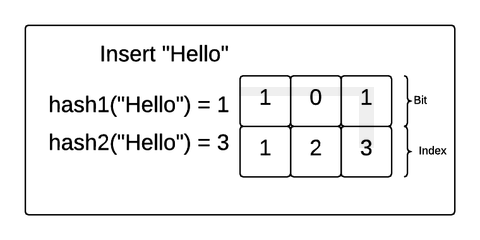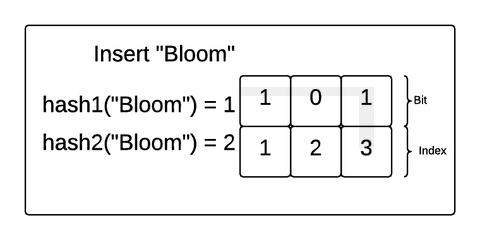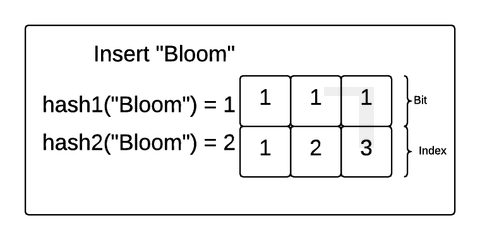
Bloom Filter

Problem: to find out that value doesn't exist in SSTable we have to look over memtable and then all segments (each might require a disk read)

Bloom filter: m-bit array, k hash functions. On insert put 1 into the bit of corresponding hash- function. On search check, if those bits are all 1s. If not then miss

Compacting Strategies

In size-tiered compaction, newer and smaller SSTables are successively merged into older and larger SSTables.

 

In leveled compaction, the key range is split up into smaller SSTables and older data is moved into separate “levels,” which allows the compaction to proceed more incrementally and use less disk space.

B-Trees

 The log-structured (SSTables) indexes we saw earlier break the database down into variable-size segments, typically several megabytes or more in size, and always write a segment sequentially.  

 

 

By contrast, B-trees break the database down into fixed-size pages, traditionally 4 KB in size (sometimes bigger), and read or write one page at a time. This design corresponds more closely to the underlying hardware, as disks are also arranged in fixed-size blocks.

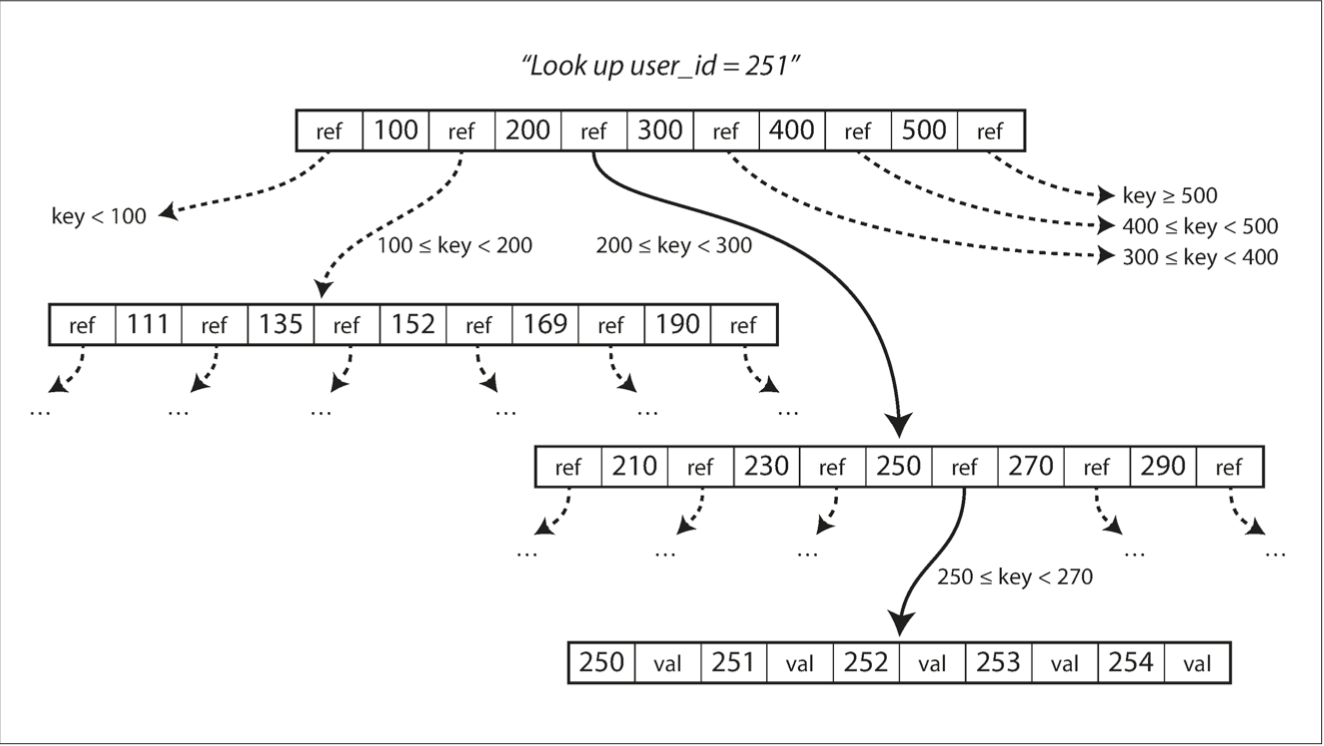
B-Trees - Lookup

Each page can be identified using an address or location,

Page can have a ref/pointer to another page

branching factor - number of references within one page to other pages (typically several hundred) 

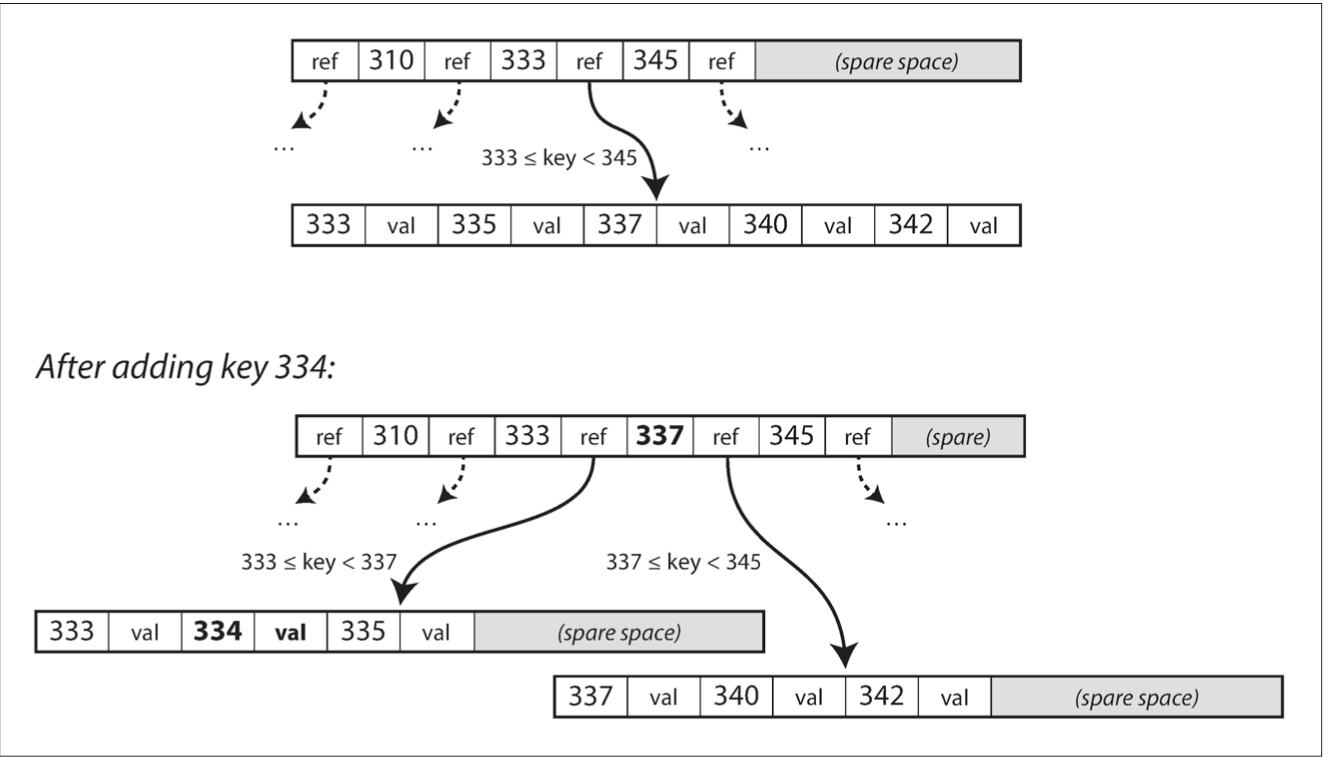
B-Trees - Writes

If not enough space - split the page into 2

Due to fix-sized nodes - the tree is balanced meaning O(logN) depth

A four-level tree of 4 KB pages with a branching factor of 500 can store up to 256 TB.

B-Trees - Reliability

Problem: some operations require several different pages to be overwritten (in case of error page might be orphaned)

Solution1: additional write-ahead log (WAL, also known as a redo log) on disk

 

Problem: dirty reads in case of multiple threads

Solution: latches (lightweight locks)

 

B-Trees - Optimisations

write the updated page to a separate file + update the reference in parent. Solves dirty read issues as well

 

store abbreviation of the delimiter key for saving space

 

store pages sequentially (difficult to maintain though)

 

pointers to siblings

 

 

B-Trees - LSM-Trees

LSM has less write amplification

Better compression and don't need extra empty space

LSM has reduced fragmentation

 

 

The compaction process in LSM can interfere with writes so compaction never happens

B-Trees are better for transactions - easier to lock

 

Secondary Indexes

Since they are not unique we can either store multiple values or append primary key to the secondary index key

Heap file - where all data lies unstructured. When a row is updated and a new value requires more space we can update all refs or just create and put ref in an old place of the row

Clustered index - store value in index itself rather than in heap. Fast read but burden on writes and transactions since the value is duplicated

A mix of both approaches is called covering index or index with included columns.

Concatenated index - ordered set of keys of multiple columns. Cannot search just by second or n-th index

Multi-dimensional indexes (R-tree) - search by several dimensions at the same time (time + temperature, long + lat)

Secondary Indexes

Since they are not unique we can either store multiple values or append primary key to the secondary index key

Heap file - where all data lies unstructured. When a row is updated and a new value requires more space we can update all refs or just create and put ref in an old place of the row

Clustered index - store value in index itself rather than in heap. Fast read but burden on writes and transactions since the value is duplicated

A mix of both approaches is called covering index or index with included columns.

Concatenated index - ordered set of keys of multiple columns. Cannot search just by second or n-th index

Multi-dimensional indexes (R-tree) - search by several dimensions at the same time (time + temperature, long + lat)