Chapter 6:
The Junction Tree Algorithm
slabod@, 26.01.2018
В прошлой серии
Factor graphs
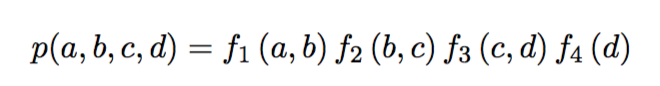
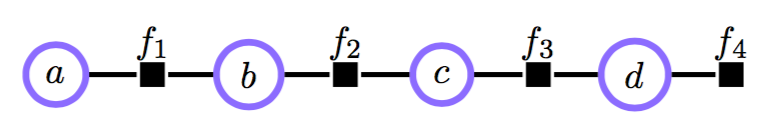
В прошлой серии
Factor graphs: single-connected
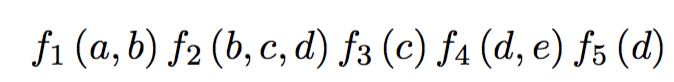

В прошлой серии
Marginal inference,
элиминация переменных
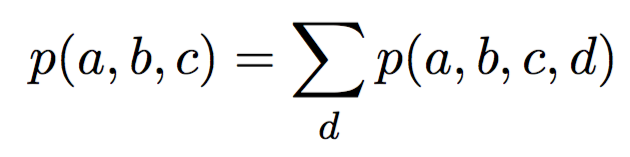
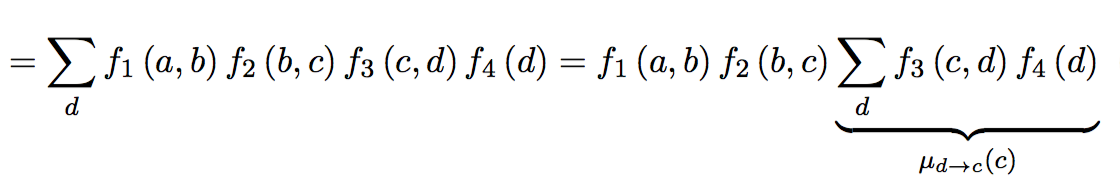
В прошлой серии
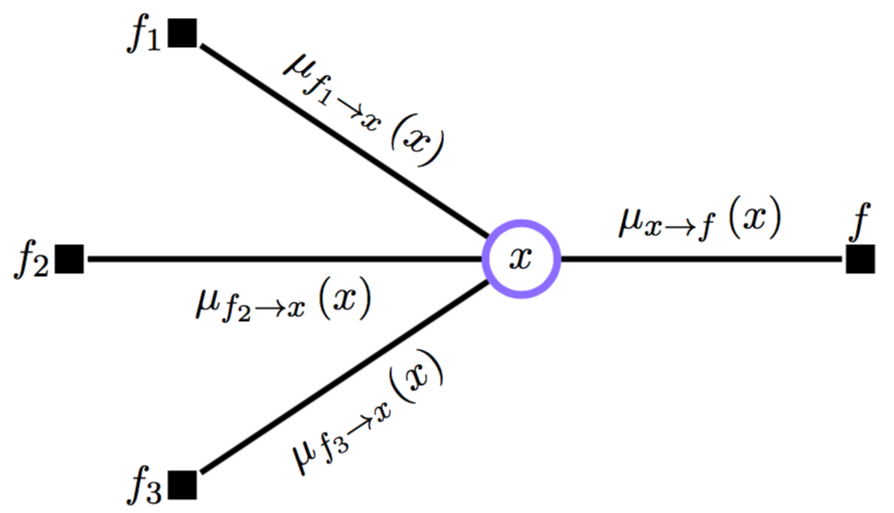
Передача сообщений

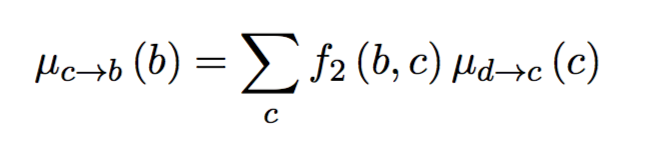
Репараметризация
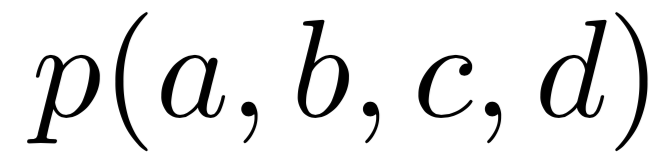

=
?
p(b, c) \,=\, \sum\limits_{a, d} p(a,b) p(b,c) p(c,d) \,=\,
=\, p(b,c) \sum\limits_{a} p(a,b) \sum\limits_{d} p(c,d) \,=\, p(b)p(b,c)p(c)
Репараметризация
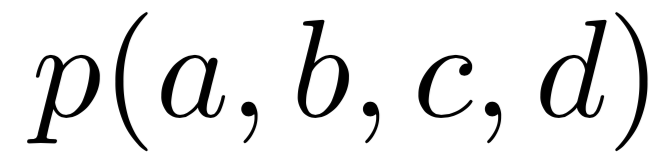
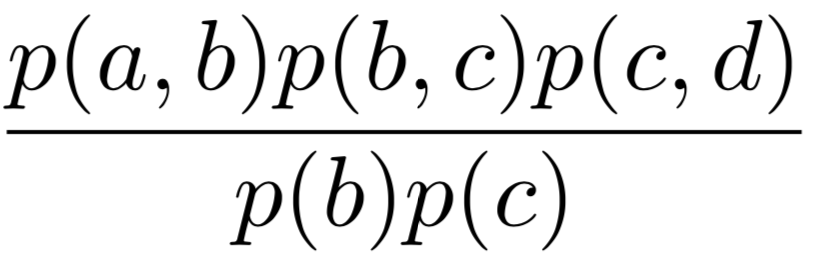
=
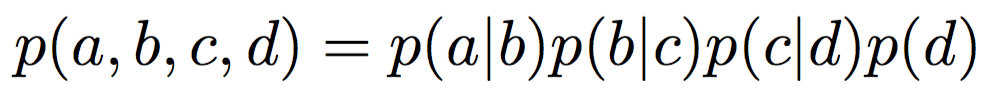
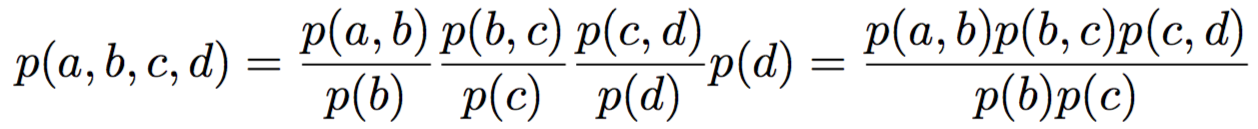
Clique Graphs


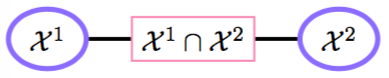
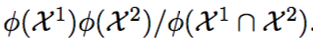
Clique Graphs: пример
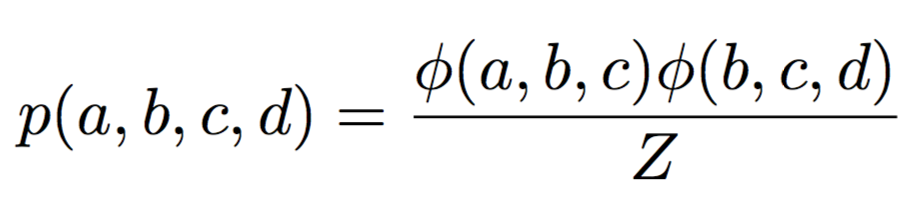
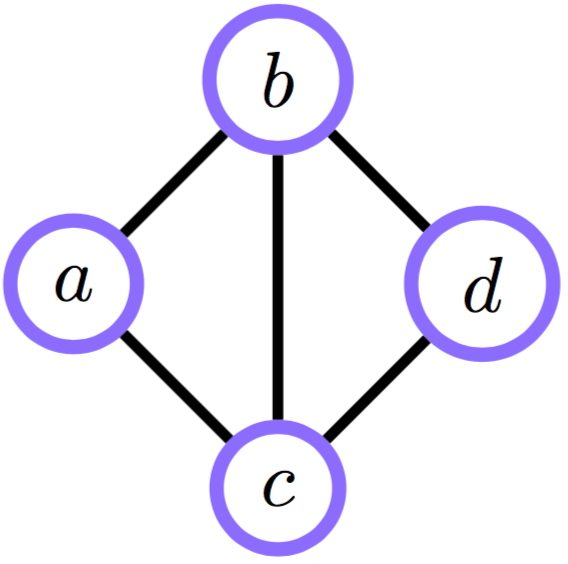
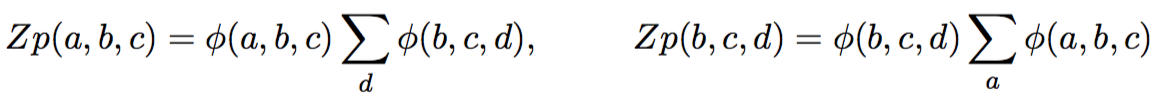
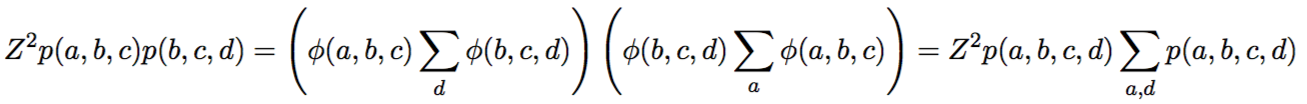
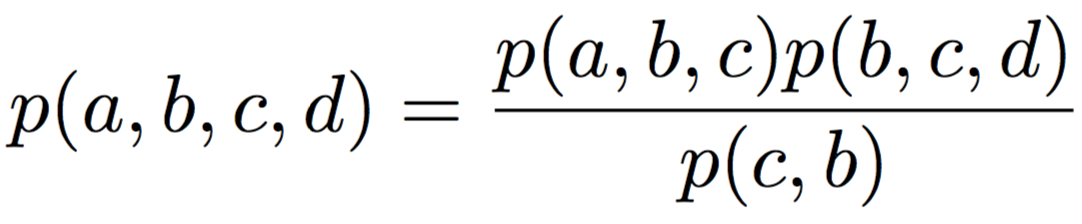
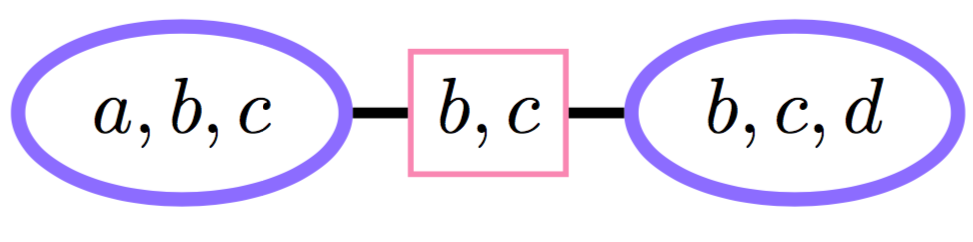
Clique Graphs: пример
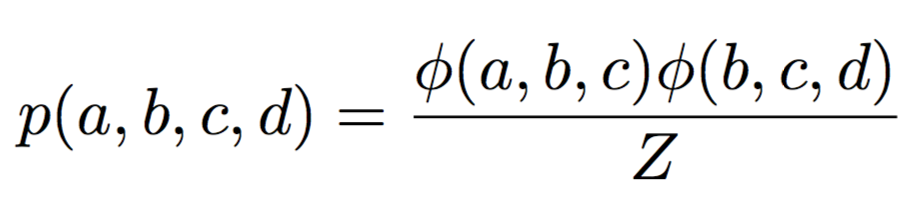

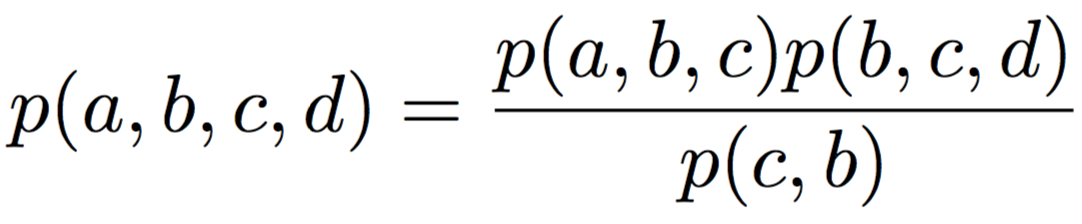
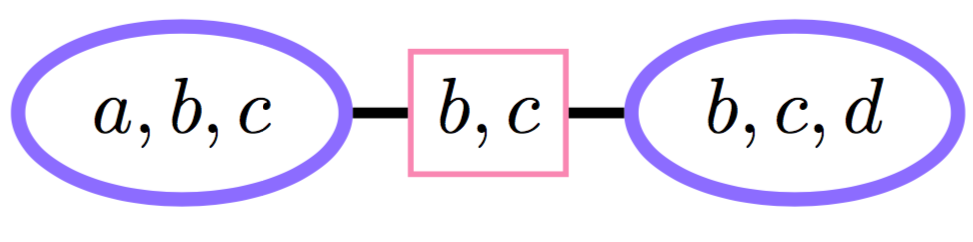
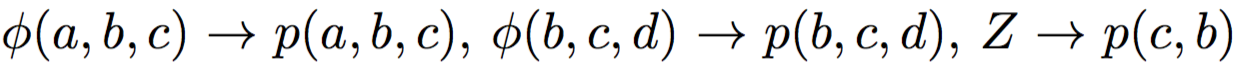
Junction Tree Algorithm: обобщение
Absorption (Поглощение)
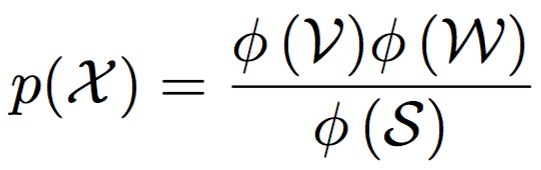
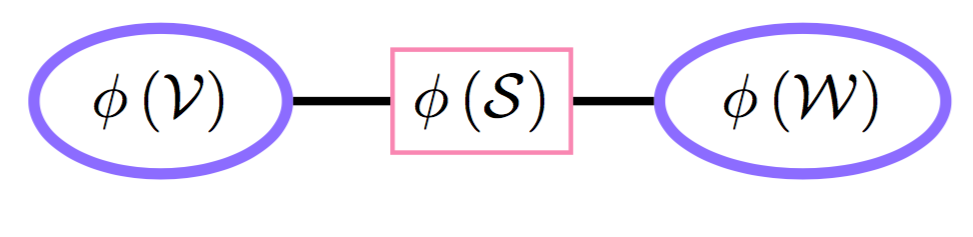
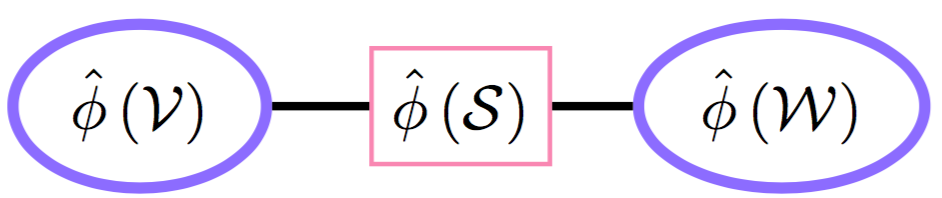
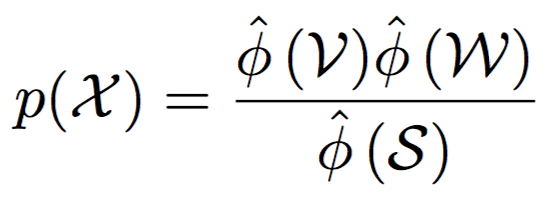

Absorption: явное вычисление
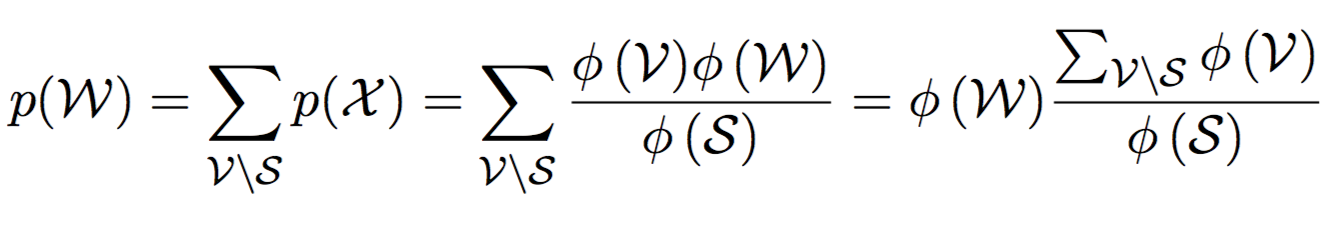
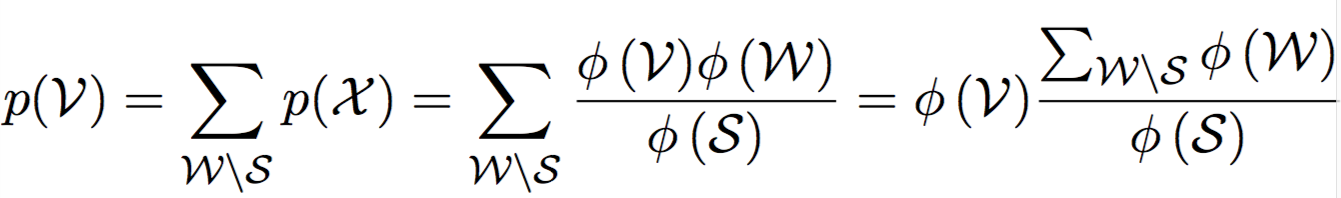
Absorption: определение

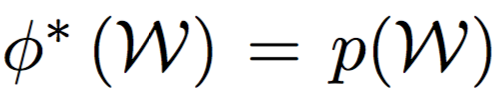
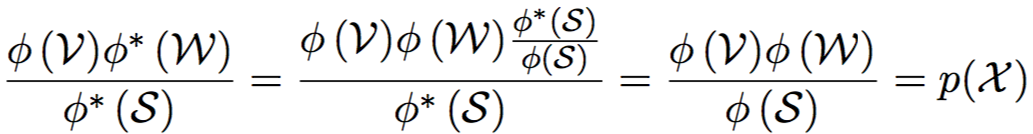
Absorption: обратный проход
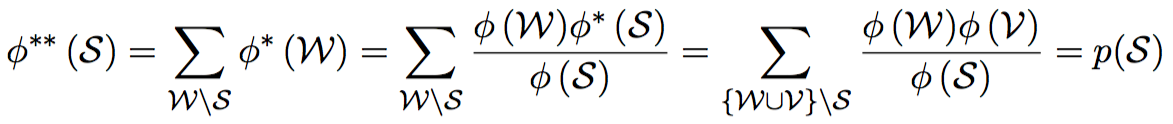
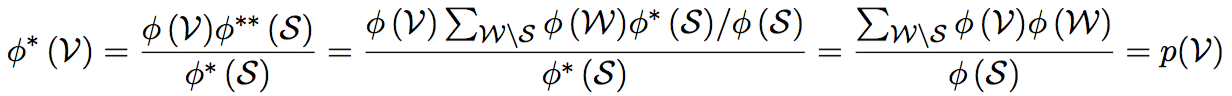
Absorption: график поглощений
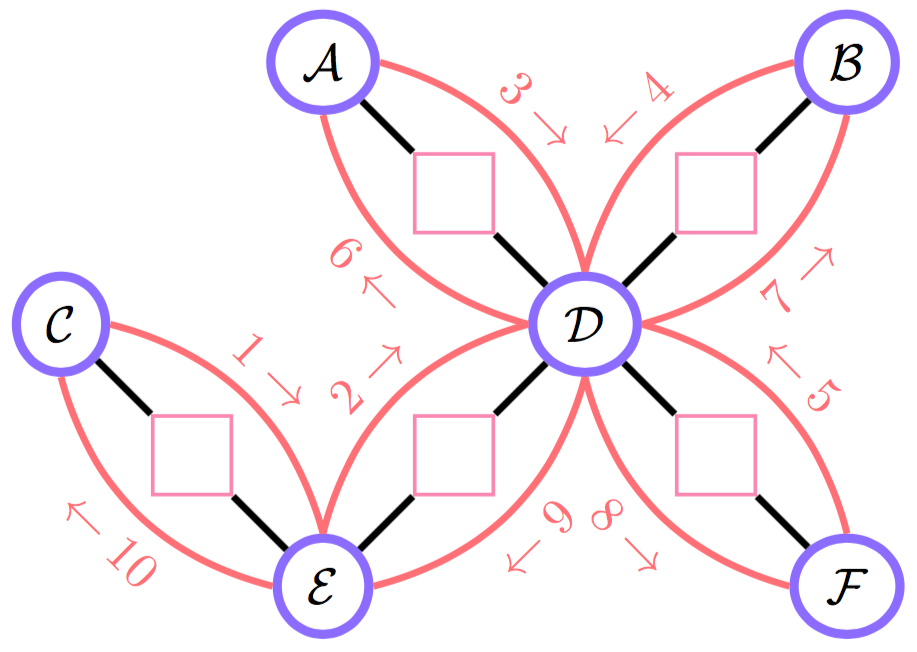

Junction tree
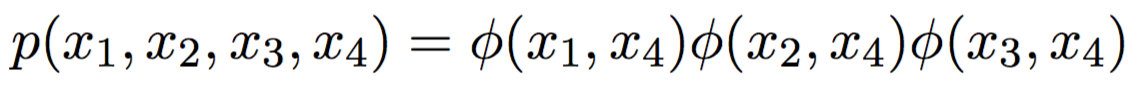
Junction tree
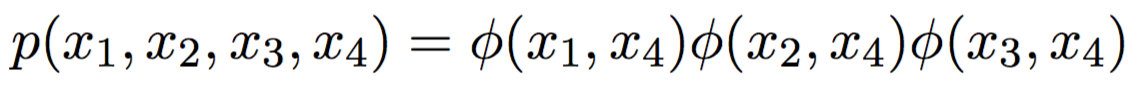
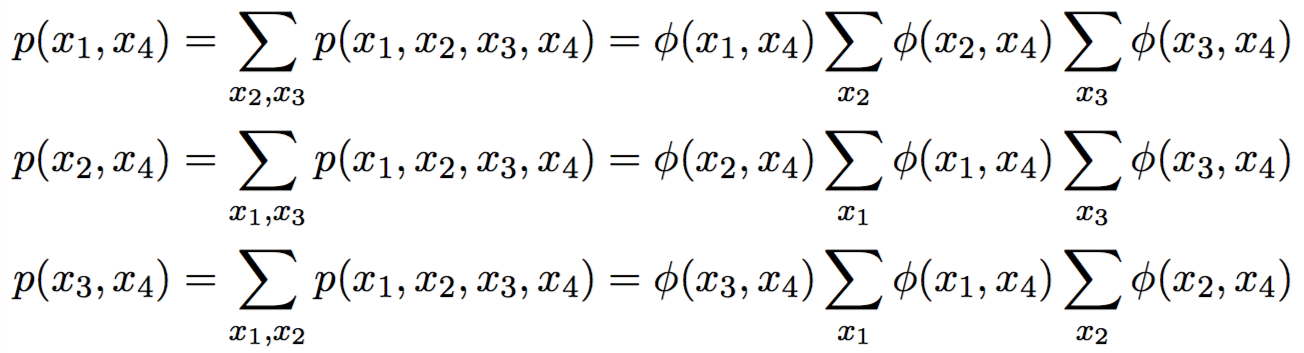
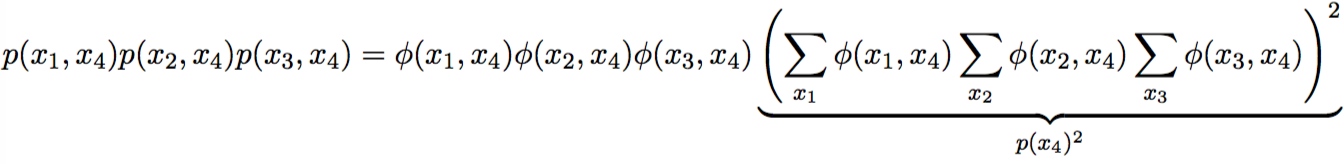
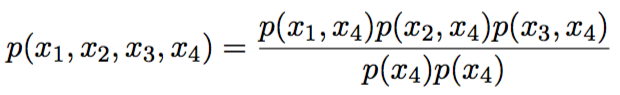
Junction tree

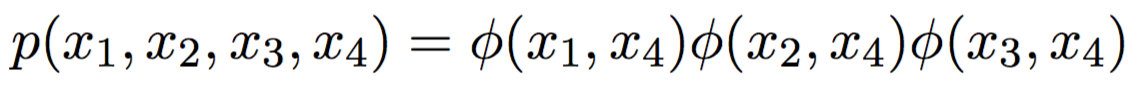
\Rightarrow
Junction tree: the running intersection & consistency


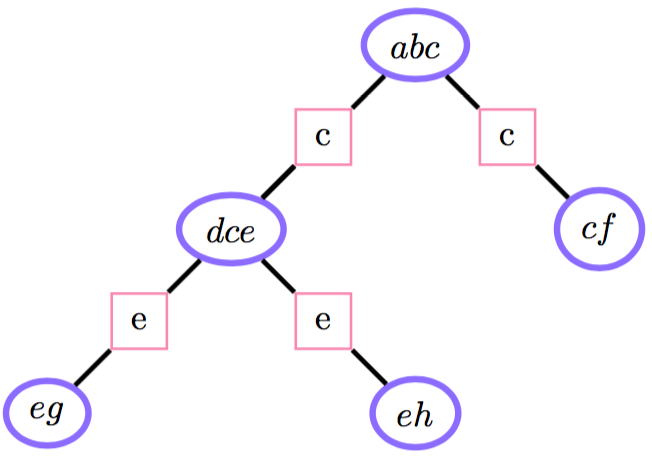
Junction tree: the running intersection & consistency
Последовательность поглощений
локальная содержательность
Running intersection
глобальная содержательность
возможность вывода маргинального представления
\Rightarrow
\Rightarrow
\Rightarrow
Junction tree: the running intersection. Пример
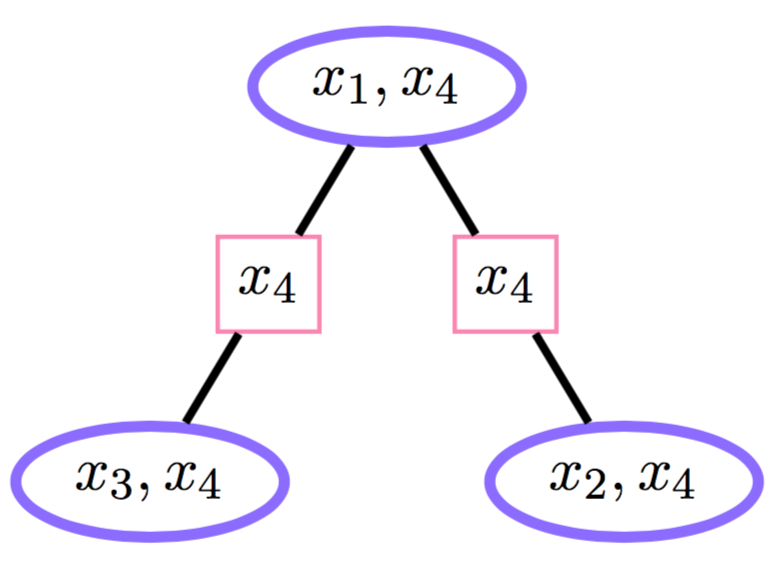
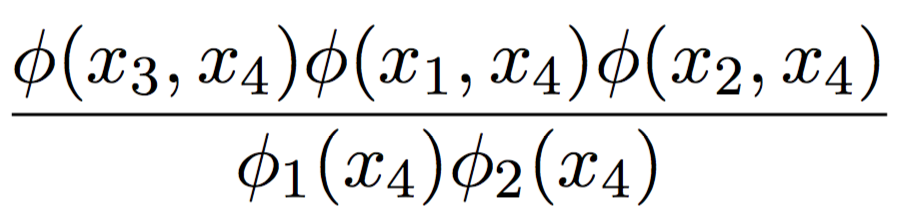
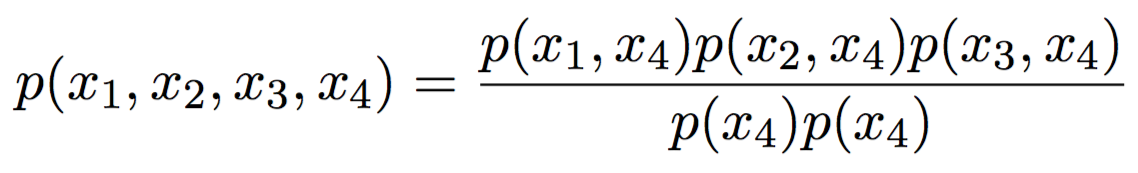
\Rightarrow
Junction tree:
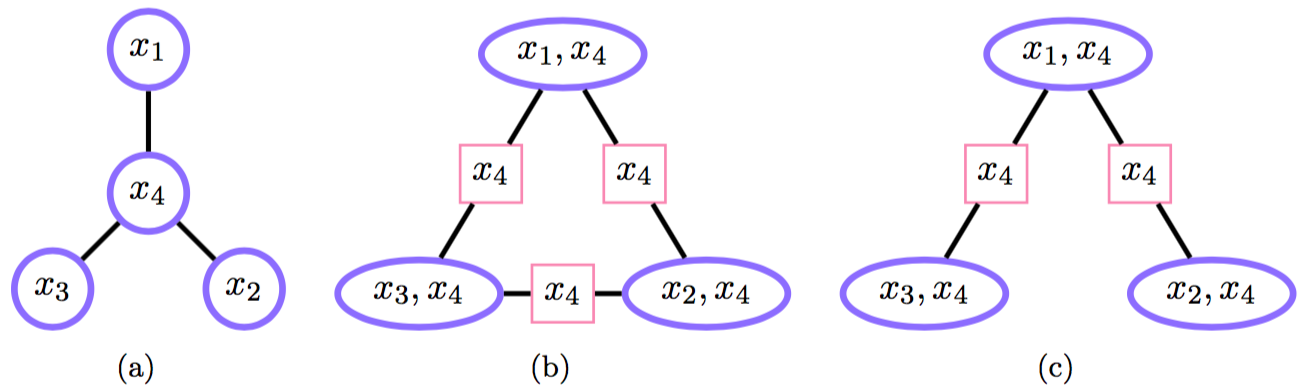
Построение для односвязных распределений
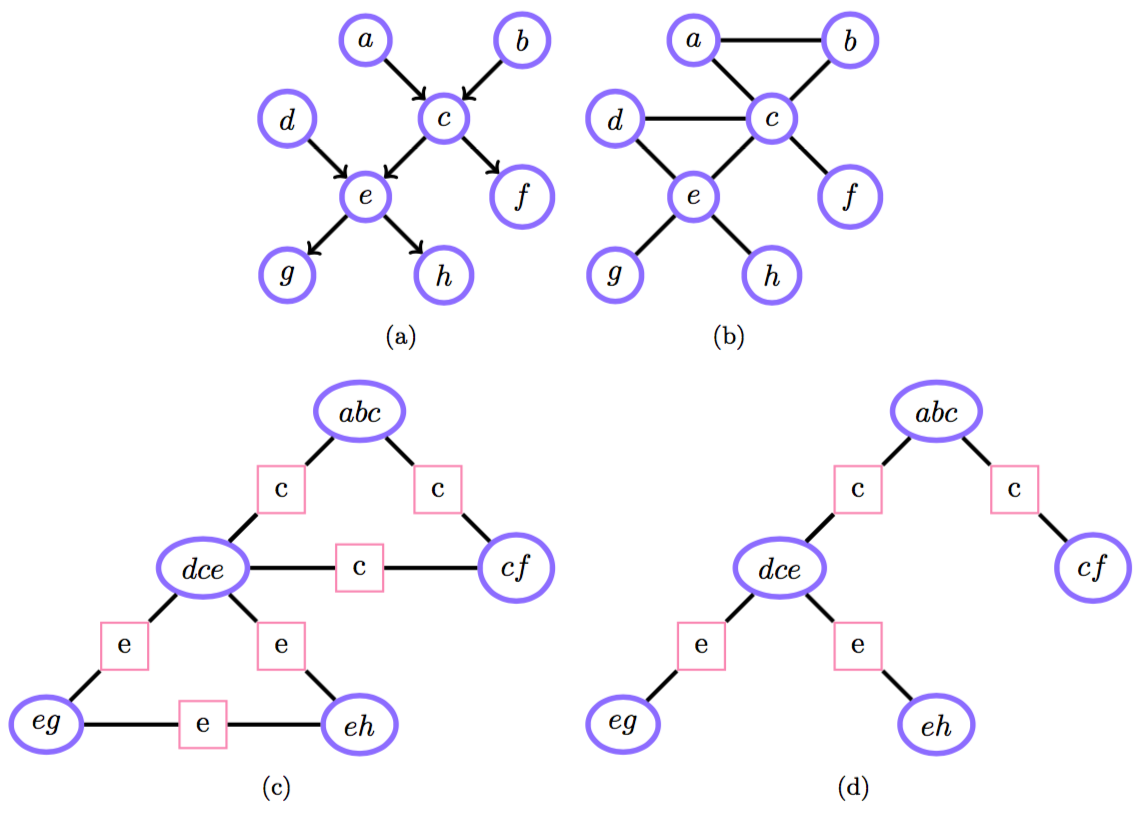

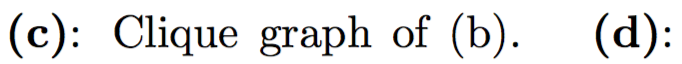
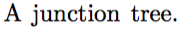
Junction tree:
Построение для односвязных распределений

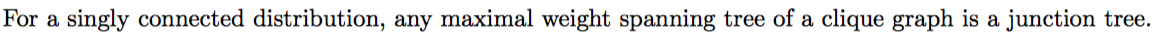
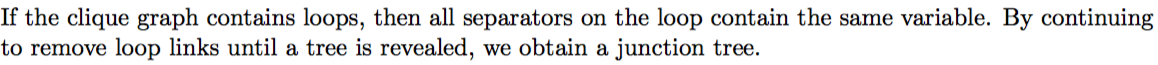
Junction tree: задание потенциалов
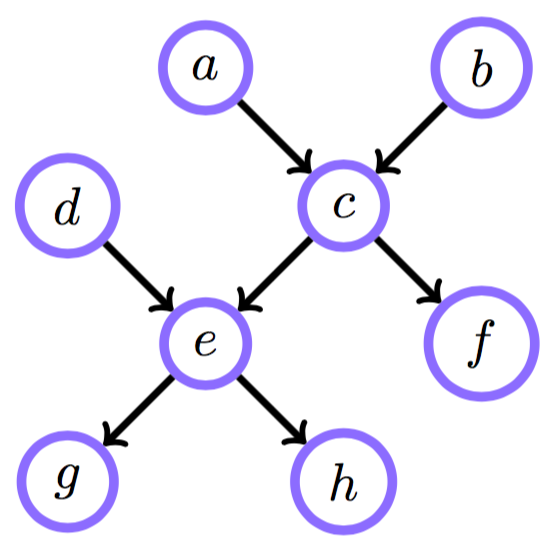
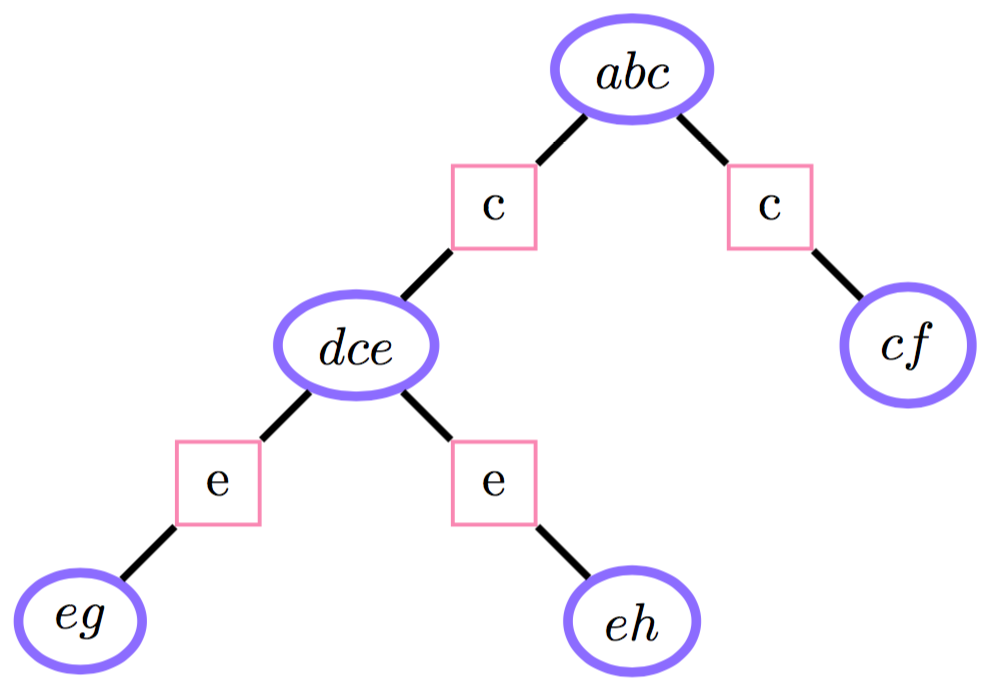
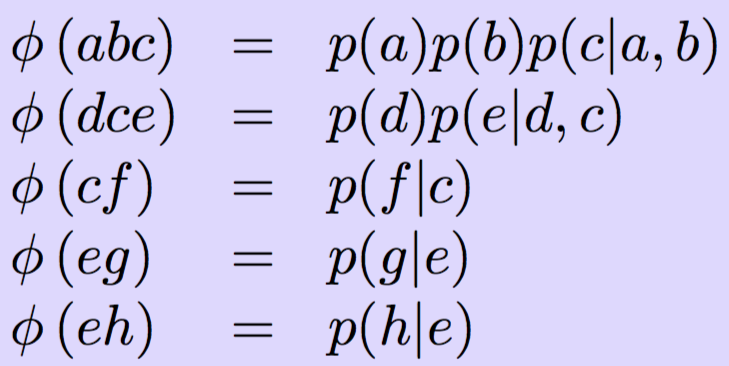
Junction tree для многосвязных распределений.
Триангуляция.

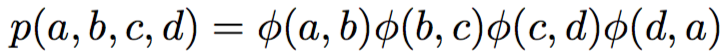

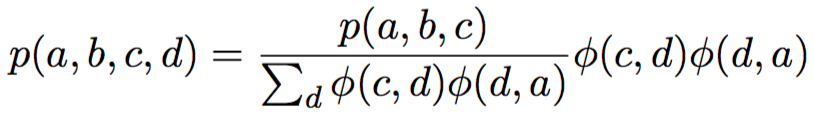

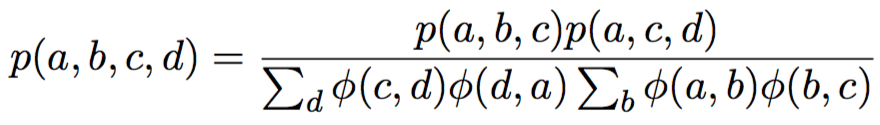

\Rightarrow
\Rightarrow
\Rightarrow
\Rightarrow
Триангуляция.
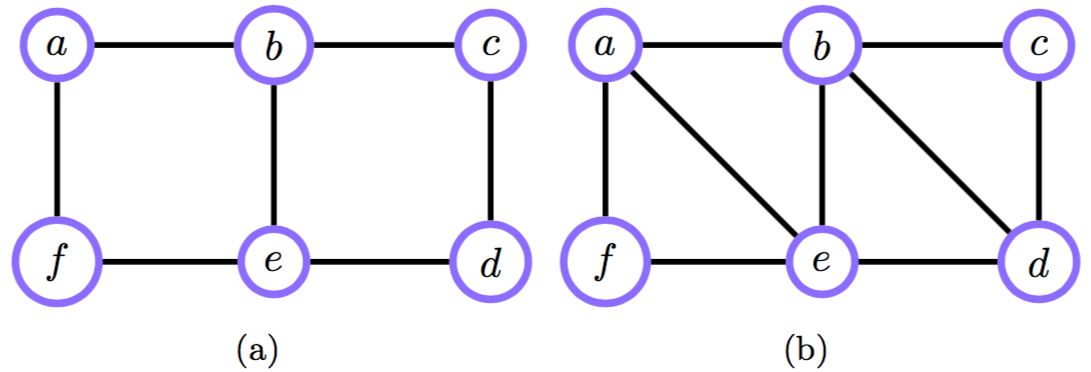
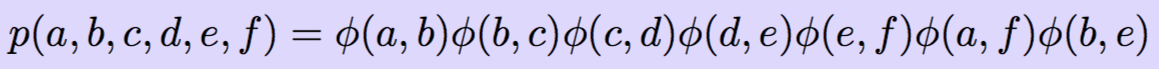

Триангуляция влияет на эффективность вывода

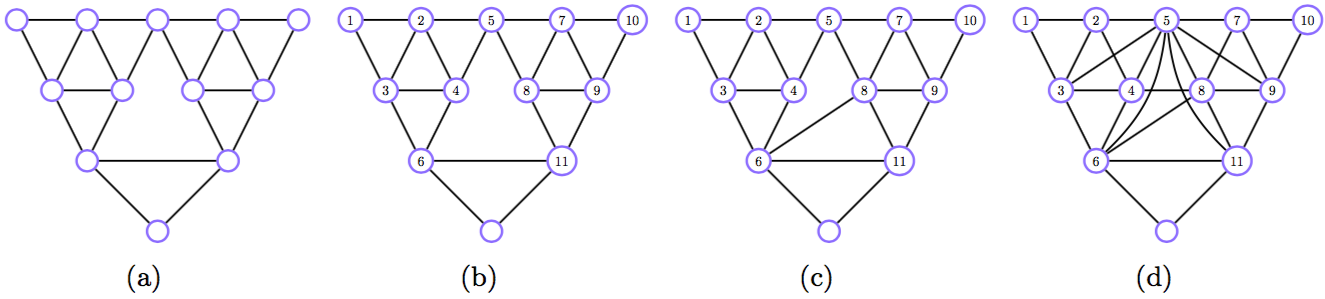
The Junction Tree Algorithm

JTA: пример

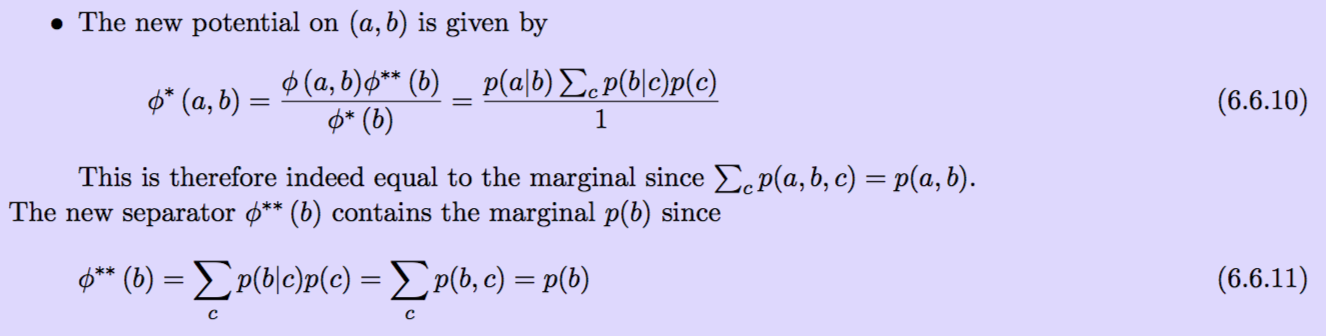
JTA: применение. Нормировочная константа
Локальная содержательность
Можно отрезать висячие вершины
\Rightarrow
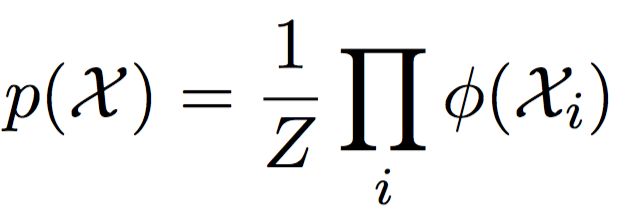
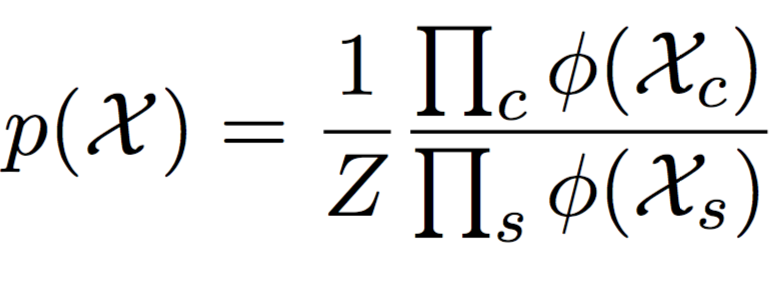
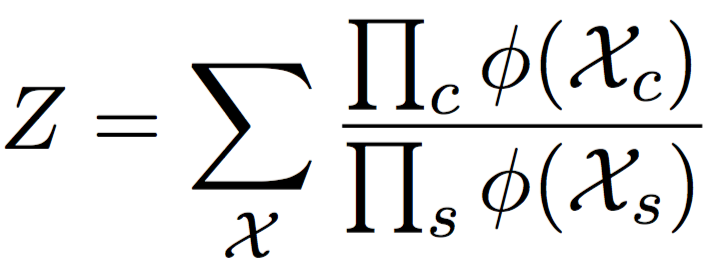
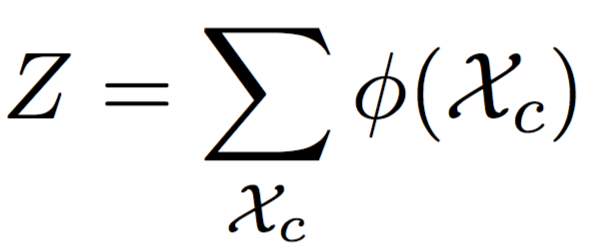
\Rightarrow
JTA: применение. Наиболее вероятное состояние

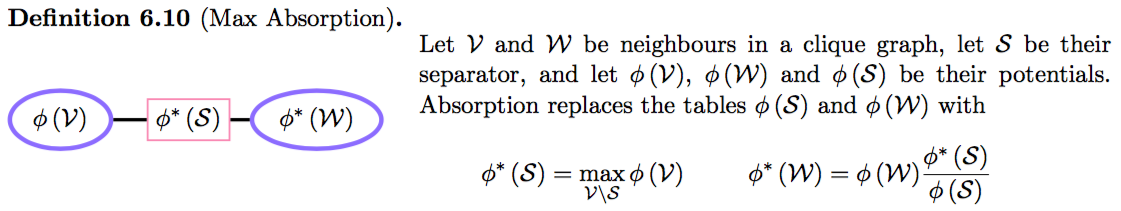
JTA. Shafer-Shenoy propagation
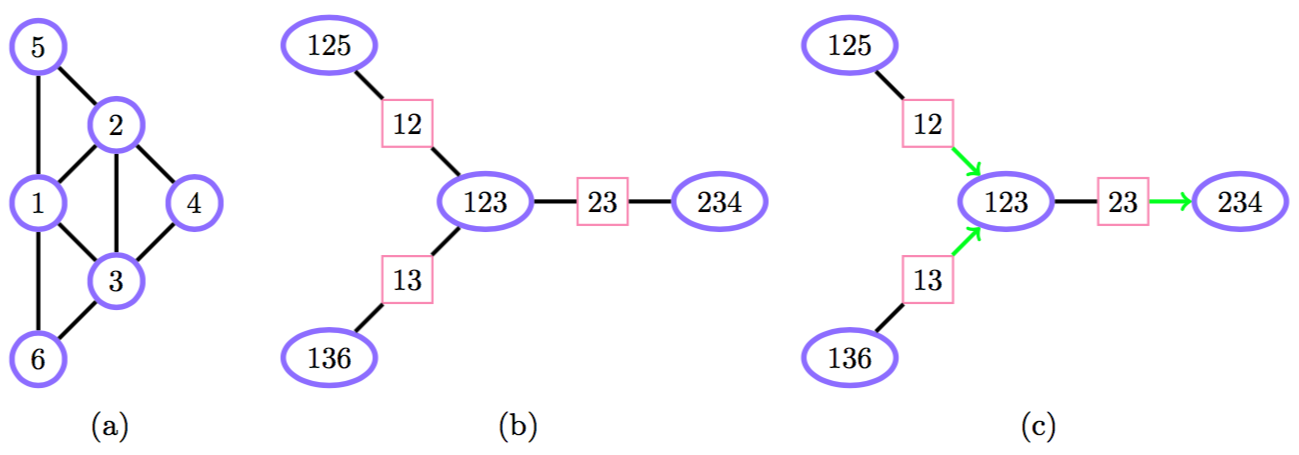
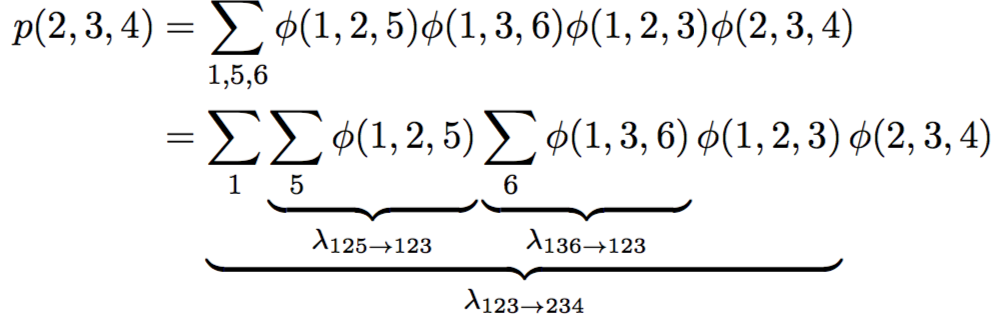
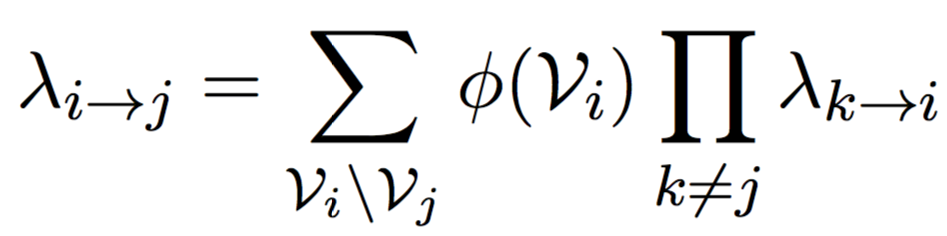
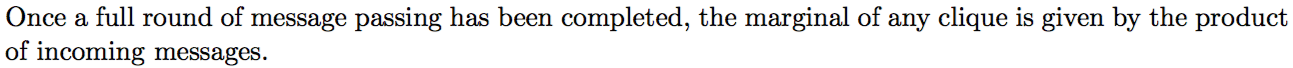
JTA. Приближения.
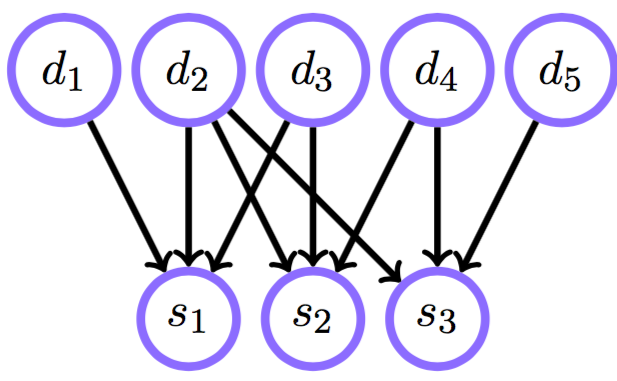
После триангуляции граф на
\{d_i\} = K_5
Спасибо за внимание!
Chapter 6
By Michael Slabodkin
Chapter 6
Chapter 6 of «Bayesian Reasoning and Machine Learning»
- 183



