«Position Auctions»
by Hal R. Varian, 2006
slabod@
MEM-seminar, 26.07.2018
Введение
$$x_1, p_1, v_1$$
$$x_2, p_2, v_2$$
$$x_3, p_3, v_3$$
$$x_4, p_4, v_4$$
\ge
\ge
\ge
Формализация
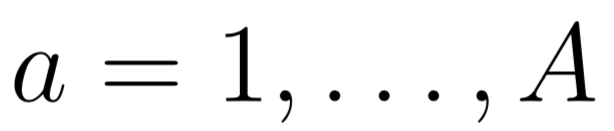
- участники
- позиции
- CTR — clickthrough-rate
для
$$A > S$$
Ценность клика
для \(a\) ценность \(v_1\)
выгода \(u_{as} = v_a x_s\)
порядок \(b_1 > b_2 > \ldots > b_A\)
цены \(p_i = b_{i + 1}\)
\(v_s, \, x_s, \, p_s = b_{s + 1}, \, u_s\)
Net profit
Nash equilibrium
известно:
Symmetric Nash equilibrium
\Leftrightarrow
SNE \(\subseteq\) NE
Неотрицательная выгода
Возрастающая ценность клика
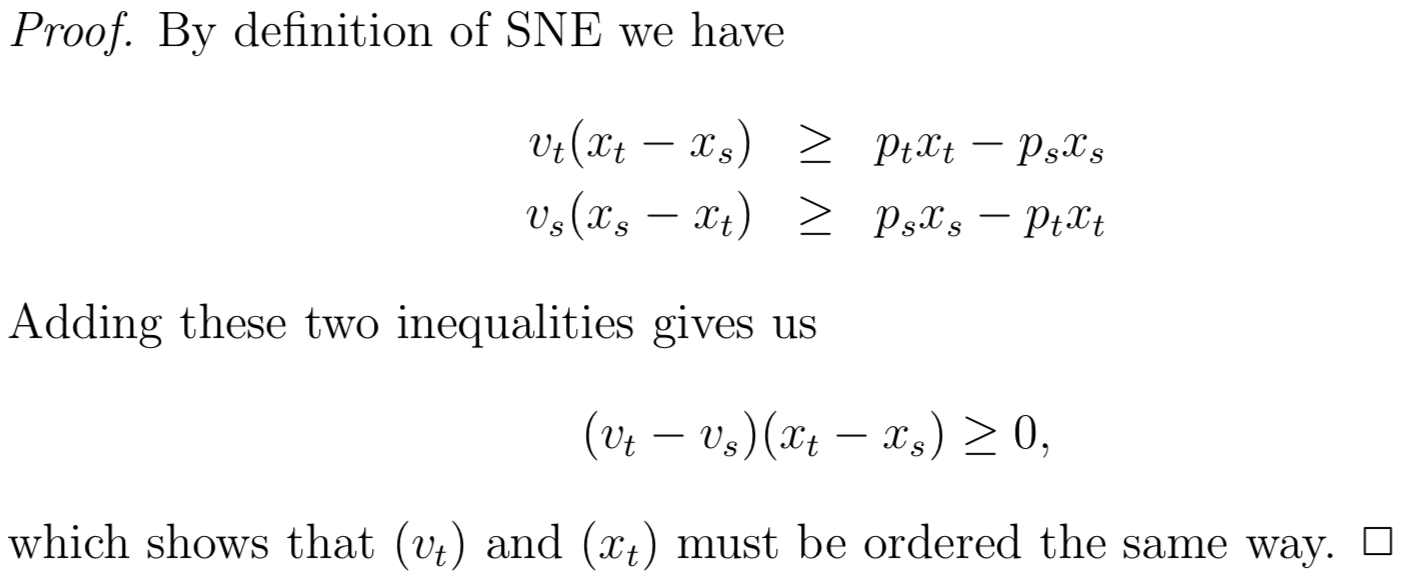
Возрастающие цены (?!)
Возрастающие цены (!)
+ \, \{\ldots\}
\Rightarrow
SNE
NE
\Rightarrow
SNE
\Rightarrow
Проверка одного шага
Явное решение SNE
s \rightarrow s + 1
s + 1 \rightarrow s
\Rightarrow
\Rightarrow
\Rightarrow
\Rightarrow
\Rightarrow
Верхнее и нижнее решение
\Rightarrow
\Rightarrow
Крайний случай рекурсии
\Rightarrow
\Rightarrow
Первый исключённый ставит свою ценность
≈ Vickrey auction
Граничные значения
выгода на позиции \(s \: = \)
максимальная ставка, пока \(s + 1\) не захочет поменяться:
\Rightarrow
Граничные значения
выгода на позиции \(s \: = \)
максимальная ставка без убытка при обмене с \(s + 1\):
\Rightarrow
NE revenue vs SNE revenue
NE revenue vs SNE revenue
— максимум NE
— максимум SNE
\Rightarrow
\ge
\Rightarrow
\Rightarrow
\ge
NE revenue vs SNE revenue
Vickrey-Clarke-Groves (VCG) mechanism
z \in Z
Доказательство truthfulness
1. Честный вариант
=
2. Нечестный вариант
сообщили \(r_a(.)\)
сообщили \(r'_a(.)\)
u_a(z') + \sum\limits_{b \neq a} r_b(z') \,\le\, r_a(z) + \sum\limits_{b \neq a} r_b(z)
= \max\limits_{x} \, \{\, u_a(x) + \sum\limits_{b \neq a} r_b(x) \,\}
VCG для position auctions
цена
Bounds on values
\Rightarrow
\Rightarrow
\Rightarrow
\Rightarrow
Bounds on values
\Rightarrow
- Условия существования решения
- Механизм определения \(b_a\)
- Возрастание marginal cost клика
\Rightarrow
Геометрическая интерпретация
Геометрическая интерпретация
Аукционы рекламы
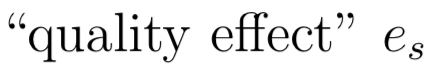
участники упорядочены по
минимальный платёж для позиции \(t\)
для участника \(s\) —
\Rightarrow
Аукционы рекламы
Nash equilibrium
\Rightarrow
\Rightarrow
\Rightarrow
Аукционы рекламы
Эмпирический анализ
Эмпирический анализ
Эмпирический анализ
Спасибо за внимание!
Position Auctions, Varian, 2006
By Michael Slabodkin
Position Auctions, Varian, 2006
«Position Auctions» by Hal R. Varian, 2006
