Michael Recachinas
Software Engineer by day, Puppy dad by night


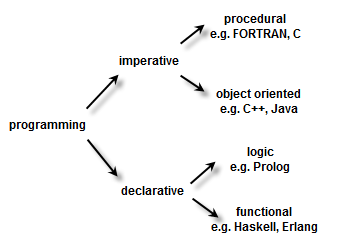
1930s – Alonzo Church & λ-calculus
1958 – John McCarthy & Lisp
1972 – Dennis Ritchie & C
(for perspective)
1973 – Robin Milner & ML
1977 – John Backus & Functional Programming

count :: List -> Int int count(List l) { ... }
Given that FP seeks to eschew side effects, reassignment is usually not valid.
let x = 3;;
x = 4;; (* => bool = false, '=' here is actually testing equality *)
x := 4;;(* => Error: This expression has type int but an expression was
expected of type 'a ref *)
Also, as previously mentioned, functions do not mutate state, they only return new values.
let arr = [1; 2; 3] (* declare a list *)
double arr (* => [2; 4; 6], arr has not changed *)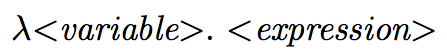
λx. x == function(x) { return x; }
λx. y == function(x) { return y; }
λx. x UNICORN == function(x) { return x; }(UNICORN) // => UNICORN
λs. (s s) == function(f) { return f(f); }
λs. (s s) λs. (s s) == function(f) { return f(f); }(function(f) { return f(f); })=> λs. (s s) λs. (s s) => λs. (s s) λs. (s s) => ...
f :: A → B add1 :: integer → integer
map(function, array) # => new array var f = function(x) { return 2 * x; };
var double = { name: 'double' };
double.fn = f;
double.fn(3) // => 6
map(function, iterable, ...)
map :: (a → b) → [a] → [b] def square(x): return x ** 2
map(square, [1, 2, 3, 4, 5]) # => [1, 4, 9, 16, 25] reduce(function, iterable, initializer=None) What's its type?
reduce (aka fold) :: (a → b → b) → b → [a] → b def mult(x,y): return x * y
reduce(mult, [1, 2, 3, 4, 5], 1) # => 120 filter(function, iterable) filter : (a → boolean) → [a] → [a] def is_even(x): return x % 2 == 0
filter(is_even, [1, 2, 3, 4, 5]) # => [2, 4]
lambda arguments: expression def f(x): return x ** 2 # regular function
g = lambda x: x ** 2 # lambda, or anonymous function
f(8) # => 64
g(8) # => 64 map(lambda x: x ** 2, [1, 2, 3, 4, 5] # => [1, 4, 9, 16, 25]
reduce(lambda x,y: x * y, [1, 2, 3, 4, 5], 1) # => 120
filter(lambda x: x % 2 == 0, [1, 2, 3, 4, 5]) # => [2, 4]
nest = lambda x: lambda y: lambda z: x + y + z
nest(1)(2)(3) # => 6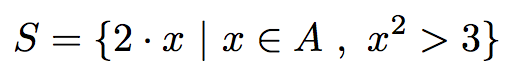
a_list = [1, 2, 3, 4, 5]
S = [ 2 * x for x in a_list if x ** 2 > 3 ] # => [4, 6, 8, 10]def qsort(L):
if len(L) <= 1: return L
return qsort( [ lt for lt in L[1:] if lt < L[0] ] ) + \
[ L[0] ] + qsort( [ ge for ge in L[1:] if ge >= L[0] ] )
a_list = [1, 2, 3, 4, 5, 6]
S = ( 2 * x for x in a_list if x ** 2 > 3 ) # => <generator object
<genexpr> at 0x221164>
S.next() # => 4
S.next() # => 6
S.next() # => 8
S.next() # => 10
S.next() # => 12 def make_incrementor(n): return lambda x: x + n
f = make_incrementor(1) # => (lambda x: x + 1)
g = make_incrementor(10)# => (lambda x: x + 10)
f(5) # => 6
g(5) # => 15
def logger(func):
def inner(*args, **kwargs):
print "Arguments were: %s, %s" % (args, kwargs)
return func(*args, **kwargs)
return inner
@logger
def foo(x, y): return x * y
foo(5, 4) # => 20, output=Arguments were: (5, 4), {} @total_ordering # this is a decorator, you supply __eq__ and such
class Student:
def __eq__(self, other):
return ((self.lastname.lower(), self.firstname.lower()) ==
(other.lastname.lower(), other.firstname.lower()))
def __lt__(self, other):
return ((self.lastname.lower(), self.firstname.lower()) <
(other.lastname.lower(), other.firstname.lower()))from functools import partialbasetwo = partial(int, base=2) # int takes in int(x, base=10) basetwo('10010') # => 18 (((a → b) → c) → a) → (b → c) = λ(f, x). λy. f (x, y) // watimport itertools chain('ABC', 'DEF') # => A B C D E F
compress('ABCDEF', [1,0,1,0,1,1]) # => A C E F
dropwhile(lambda x: x<5, [1,4,6,4,1]) # => 6 4 1
ifilter(lambda x: x%2, range(10)) # => 1 3 5 7 9
ifilterfalse(lambda x: x%2, range(10)) # => 0 2 4 6 8
imap(pow, (2,3,10), (5,2,3)) # => 32 9 1000
starmap(pow, [(2,5), (3,2), (10,3)]) # => 32 9 1000
takewhile(lambda x: x<5, [1,4,6,4,1]) # => 1 4
izip('ABCD', 'xy') # => Ax By
izip_longest('ABCD', 'xy', fillvalue='-') # => Ax By C- D-
permutations('ABCD', 2) # => AB AC AD BA BC BD CA CB CD DA DB DC
combinations # => AB AC AD BC BD CD
combinations_with_replacement('ABCD', 2) # => AA AB AC AD BB BC BD CC CD DD

var arr = [1, 2, 3, 4, 5]
arr.map(function(element) { return Math.pow(element, 2); });
// => [1, 4, 9, 16, 25]; arr is still [1, 2, 3, 4, 5]
arr.filter(function(element) { return x % 2 === 0; });
// => [2, 4]; arr is still [1, 2, 3, 4, 5]
arr.reduce(function(prev, current, index, array) {
return prev * current;
});
// => 120; arr is still [1, 2, 3, 4, 5] $('#yolo').click( function() { // Even in jQuery too!
alert("swag!")
});
var add = function(x) {
return function(y) {
return x + y;
}
};
var incrementor = add(1);
incrementor(5) // => 6 var add1 = function add1(x) { return x + 1; };
var add3 = compose(add1, add1, add1);
add3(0) // => 3 var addSalutation = function(x) { return 'G`day, ' + x; };
var addTitle = function(x) { return 'Mr. ' + x; };
var meetAndGreet = compose(addSalutation, addTitle);
addSalutation(addTitle('Baggins')); // => G`day, Mr. Baggins
meetAndGreet('Baggins'); // => G`day, Mr. Baggins var friendlyGreet = function(somebody) {
alert("Hi, " + somebody.name + ", I'm " + this.name);
};
friendlyGreet.apply(Bob, [Alice]); // => "Hi, Alice, I'm Bob" friendlyGreet.bind(Bob)(Alice); // => "Hi, Alice, I'm Bob"
friendlyGreet.call(Bob, Alice); // => "Hi, Alice, I'm Bob"
friendlyGreet.bind(Bob).call(Alice, Bob); // => "Hi, Bob, I'm Bob"

(* Comments can (* be (* nested *) *) *)
let x = ... (* This is how you define an immutable variable *)
(* The compiler infers type, so you don't need annotations! *)
let x = ref ... (* This is a reference, similar to pointers in C/C++ *)
let y = !x (* This is how you access a referenced value *)
x := !x + 1 (* This will change the contents of x to (x+1) *)
let double x = 2 * x (* == int double(x){ return 2*x; } *)
let rec fact x = function (* You have to denote recursive functions *)
| 0 -> 1 (* Pattern matching!! *)
| n -> n * fact (n-1)
let rec last = function
| [ ] -> None
| [a] -> Some(a)
| _ :: tl -> last tl let sum = List.fold_left (fun a x -> x + a) 0
let map f l = List.fold_right (fun x a -> (f x) :: a) l []
let rev l = List.fold_left (fun a x -> x :: a) [] l
let filter f l =
List.fold_right (fun x a -> if f x then x :: a else a) l []
type binarytree =
| Node of binarytree * int * Node of binarytree
| Leaf of int
let rec height tree = match tree with
| Leaf _ -> 1
| Node(x,_,y) -> 1 + max (height x) (height y) qsort [] = []
qsort (p:xs) = (qsort lesser) ++ [p] ++ (qsort greater)
where
lesser = filter (< p) xs
greater = filter (>= p) xs
f x = 2 * x (* f :: Int → Int *) printf("%d", 'c' + 5); // this shouldn't work head (sort lst) # will only be sorted enough to find the minimum [1..] # infinite data structure print len([1 + 1, 2 * 2, 3 / 0, 4 - 1]) # => ZeroDivisionError: ...Replace each reference to a variable with its definition
let y = 55;;
let f x = x + y;;
f 3;; (* => 3 + y => 3 + 55 => 58 *)
# ----- Recursive, but not tail recursive -----
def fact(n):
if n == 0: return 1
return n * fact(n - 1)
# ----- Tail Recursive -----
def fact1(n, accumulator):
if n == 0: return accumulator
return fact1(n - 1, n * accumulator)
def fact(n):
return fact1(n, 1)
Don't ask me what a monad is.



[] () -> int { return 1; };
[] () { return 1; }; // compiler knows this returns an integer
Immutability

References
By Michael Recachinas