Predicting Attention Sparsity
in Transformers
May 27, 2022
Marcos Treviso
António Góis
Patrick Fernandes
Erick Fonseca
André F. T. Martins
DEEPSPIN
Interpretable heads
softmax transformer
(Voita et al., 2019)
rare tokens
Interpretable heads
softmax transformer
(Voita et al., 2019)
α-entmax transformer
(Correia et al., 2019)
rare tokens
neighboring tokens
Interpretable heads
softmax transformer
(Voita et al., 2019)
α-entmax transformer
(Correia et al., 2019)
rare tokens
neighboring tokens
both are \(\mathcal{O}(n^2)\)
Interpretable heads
softmax transformer
(Voita et al., 2019)
α-entmax transformer
(Correia et al., 2019)
rare tokens
neighboring tokens
can we save
computation?
$$O(n^2) \dots O(n) \dots O(1)$$
both are \(\mathcal{O}(n^2)\)
Subquadratic self-attention
Subquadratic self-attention
Subquadratic self-attention
Subquadratic self-attention
Subquadratic self-attention
Sparsefinder
Sparsefinder
\(\mathcal{G}_h\)
Sparsefinder
\mathcal{L}_\theta(\mathcal{G}_h) = \Big[
\omega +
\|\bm{q}' - \bm{k}'_{\text{P}}\|^2_2 -
\|\bm{q}' - \bm{k}'_{\text{N}}\|^2_2
\Big]_{+}
\(\bm{q}' = \bm{W}^Q_h \bm{q}\)
\(\bm{k}' = \bm{W}^Q_h \bm{k}\)
distance to
negative pairs
distance to
positive pairs
margin
lower
dimensionality
\(\mathcal{G}_h\)
Sparsefinder
distance-based \(\mathcal{O}(n^2)\)
\(\hat{\mathcal{G}}_h = \{(\bm{q}_i, \bm{k}_j) \mid \|\bm{q}'_i - \bm{k}'_j\| \leq t\}\)
bucketing \(\mathcal{O}(n\sqrt{n})\)
\(\hat{\mathcal{G}}_h = \{(\bm{q}_i, \bm{k}_j) \mid f(\bm{q}'_i) \cap f(\bm{k}'_j) \neq \emptyset\}\)
clustering \(\mathcal{O}(n\sqrt{n})\)
\(\hat{\mathcal{G}}_h = \{(\bm{q}_i, \bm{k}_j) \mid c(\bm{q}'_i) = c(\bm{k}'_j) \}\)
\(f\) yields bucket ids element-wise
\(c\) yields a cluster id
\(\mathcal{G}_h\)
Sparsefinder
\(\mathcal{G}_h\)
α-entmax graph
• \(\mathcal{G}\): gold \(\alpha\)-entmax graph
• \(\hat{\mathcal{G}}\): predicted graph
• \(|\mathcal{G}|\): number of edges
e.g.,
\(\mathcal{G}\): gold \(\alpha\)-entmax graph
e.g.,
\(\hat{\mathcal{G}}\): predicted graph
α-entmax graph
• \(\mathcal{G}\): gold \(\alpha\)-entmax graph
• \(\hat{\mathcal{G}}\): predicted graph
• \(|\mathcal{G}|\): number of edges
recall(\(\mathcal{G}, \hat{\mathcal{G}})\)
$$ \frac{|\mathcal{G} \cap \hat{\mathcal{G}}|}{|\mathcal{G}|} $$
recall(\(\mathcal{G}, \hat{\mathcal{G}})\)
$$ \frac{|\mathcal{G} \cap \hat{\mathcal{G}}|}{|\mathcal{G}|} $$
sparse consistency property
if \(\mathcal{G} \subseteq \hat{\mathcal{G}}\),
recall(\(\mathcal{G}, \hat{\mathcal{G}}) = 100\%\)
α-entmax graph
• \(\mathcal{G}\): gold \(\alpha\)-entmax graph
• \(\hat{\mathcal{G}}\): predicted graph
• \(|\mathcal{G}|\): number of edges
recall(\(\mathcal{G}, \hat{\mathcal{G}})\)
$$ \frac{|\mathcal{G} \cap \hat{\mathcal{G}}|}{|\mathcal{G}|} $$
sparsity(\(\hat{\mathcal{G}})\)
$$ 1 - \frac{|\hat{\mathcal{G}}|}{nm} $$
sparse consistency property
if \(\mathcal{G} \subseteq \hat{\mathcal{G}}\),
recall(\(\mathcal{G}, \hat{\mathcal{G}}) = 100\%\)
α-entmax graph
• \(\mathcal{G}\): gold \(\alpha\)-entmax graph
• \(\hat{\mathcal{G}}\): predicted graph
• \(|\mathcal{G}|\): number of edges
recall(\(\mathcal{G}, \hat{\mathcal{G}})\)
$$ \frac{|\mathcal{G} \cap \hat{\mathcal{G}}|}{|\mathcal{G}|} $$
sparsity(\(\hat{\mathcal{G}})\)
$$ 1 - \frac{|\hat{\mathcal{G}}|}{nm} $$
sparse consistency property
if \(\mathcal{G} \subseteq \hat{\mathcal{G}}\),
recall(\(\mathcal{G}, \hat{\mathcal{G}}) = 100\%\)
efficiency
as sparsity(\(\hat{\mathcal{G}}\)) \(\to 1\),
save computation (theoretically)
α-entmax graph
• \(\mathcal{G}\): gold \(\alpha\)-entmax graph
• \(\hat{\mathcal{G}}\): predicted graph
• \(|\mathcal{G}|\): number of edges
Experiments: MT and MLM
• MT: Transformer trained on IWSLT 2017 with \(\alpha=1.5\)
• MLM: RoBERTa finetuned on WikiText-103 with \(\alpha=1.5\)
• Evaluation: replace softmax attention by the approximation at test time
Experiments: MT and MLM
• MT: Transformer trained on IWSLT 2017 with \(\alpha=1.5\)
• MLM: RoBERTa finetuned on WikiText-103 with \(\alpha=1.5\)
• Evaluation: replace softmax attention by the approximation at test time
• Compare all methods with Pareto curves
- window size ∈ {0, 1, 3, 5, ..., 27}
- distance threshold ∈ {0.5, 1.0, 1.5, ..., 5.0}
- num. of buckets / clusters ∈ {2, 4, 6, ..., 20}
- num. of random blocks / global tokens ∈ {2, 4, 6, ..., 20}
Experiments: MT
EN→FR
Experiments: MT
EN→FR
Experiments: MT
EN→FR
Experiments: MT
EN→FR
Experiments: MT
EN→FR
Experiments: MT
EN→FR
EN→DE
Experiments: MT
• Attention head example
Ground-truth
Experiments: MT
• Attention head example
Sparsefinder k-means
Experiments: MT
• Attention head example
After applying 1.5-entmax
Experiments: Masked LM
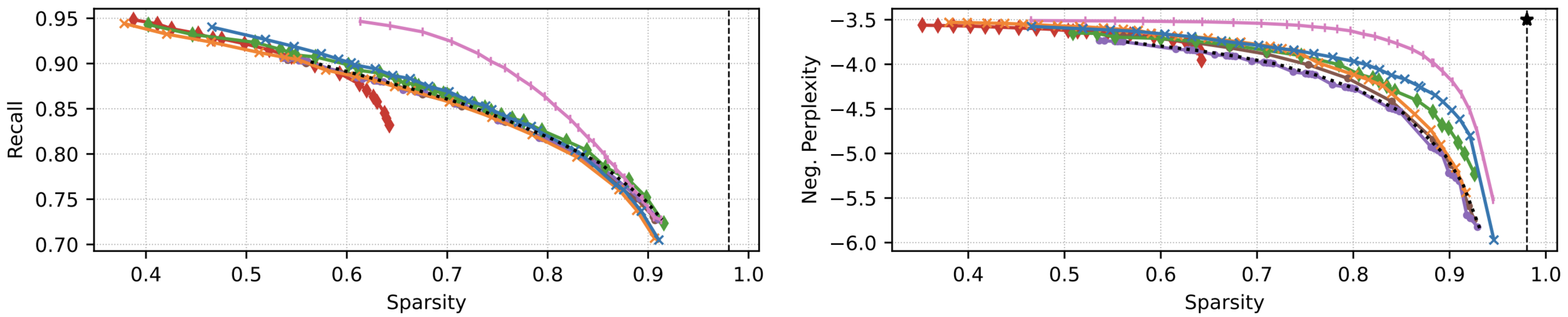
Experiments: Masked LM
• Attention head focusing on coreference tokens
Efficient Sparsefinder
• Learn projections of contiguous-chunked tokens: blocks!
Efficient Sparsefinder
• Learn projections of contiguous-chunked tokens: blocks!
• Resembles BigBird but random pattern is replaced by clustering
v1: top-k queries and keys closest to each centroid
v2: top-k queries for each clusters x top-k keys for each cluster
k = number of attended blocks
window size = 3
Efficient Sparsefinder
• Learn projections of contiguous-chunked tokens: blocks!
• Resembles BigBird but random pattern is replaced by clustering
v1: top-k queries and keys closest to each centroid
v2: top-k queries for each clusters x top-k keys for each cluster
k = number of attended blocks
window size = 3
Efficient Sparsefinder
• Learn projections of contiguous-chunked tokens: blocks!
• Resembles BigBird but random pattern is replaced by clustering
v1: top-k queries and keys closest to each centroid
v2: top-k queries for each clusters x top-k keys for each cluster
k = number of attended blocks
window size = 3
Final Remarks
Taxonomy of Efficient Transformer Architectures by (Tay et al., 2020)
Final Remarks
Taxonomy of Efficient Transformer Architectures by (Tay et al., 2020)
Sparsefinder
Final Remarks
• Avoid the full computation of the score matrix
- distance-based
- bucketing
- clustering
Final Remarks
• Avoid the full computation of the score matrix
- distance-based
- bucketing
- clustering
• Favorable sparsity-recall and sparsity-accuracy tradeoff curves
• Attention heads can remain interpretable
Final Remarks
• Avoid the full computation of the score matrix
- distance-based
- bucketing
- clustering
• Favorable sparsity-recall and sparsity-accuracy tradeoff curves
• Attention heads can remain interpretable
• Lower bound for computational sparsity
Thank you for your
attention!
Questions?
Quadratic self-attention
• Bottleneck in transformers:
...
1 2 3 4 n
\(\to \mathcal{O}(n^2)\)
Quadratic self-attention
$$O(n^2) \quad \dots \quad O(n\log n) \quad \dots \quad O(n)$$
• Bottleneck in transformers:
...
1 2 3 4 n
\(\to \mathcal{O}(n^2)\)
-💰
+🚀 -💾
+🌱
Sparsefinder
1️⃣ Extract heads from a pre-trained \(\alpha\)-entmax transformer
Sparsefinder
1️⃣ Extract heads from a pre-trained \(\alpha\)-entmax transformer
2️⃣ Learn lower dimensionality projections
\mathcal{L}_\theta(\mathcal{G}_h) = \Big[
\omega +
\|\bm{q}' - \bm{k}'_{\text{P}}\|^2_2 -
\|\bm{q}' - \bm{k}'_{\text{N}}\|^2_2
\Big]_{+}
\(\bm{q}' = \bm{W}^Q_h \bm{q}\)
\(\bm{k}' = \bm{W}^Q_h \bm{k}\)
negative pair
positive pair
margin
Sparsefinder
1️⃣ Extract heads from a pre-trained \(\alpha\)-entmax transformer
2️⃣ Learn lower dimensionality projections
3️⃣ Group \(\langle\bm{q},\bm{k}\rangle\) and compute attention within groups
\mathcal{L}_\theta(\mathcal{G}_h) = \Big[
\omega +
\|\bm{q}' - \bm{k}'_{\text{P}}\|^2_2 -
\|\bm{q}' - \bm{k}'_{\text{N}}\|^2_2
\Big]_{+}
\(\bm{q}' = \bm{W}^Q_h \bm{q}\)
\(\bm{k}' = \bm{W}^Q_h \bm{k}\)
negative pair
positive pair
margin
Sparsefinder
1️⃣ Extract heads from a pre-trained \(\alpha\)-entmax transformer
2️⃣ Learn lower dimensionality projections
3️⃣ Group \(\langle\bm{q},\bm{k}\rangle\) and compute attention within groups
\mathcal{L}_\theta(\mathcal{G}_h) = \Big[
\omega +
\|\bm{q}' - \bm{k}'_{\text{P}}\|^2_2 -
\|\bm{q}' - \bm{k}'_{\text{N}}\|^2_2
\Big]_{+}
\(\bm{q}' = \bm{W}^Q_h \bm{q}\)
\(\bm{k}' = \bm{W}^Q_h \bm{k}\)
negative pair
positive pair
distance-based
\(\hat{\mathcal{G}}_h = \{(\bm{q}_i, \bm{k}_j) \mid \|\bm{q}'_i - \bm{k}'_j\| \leq t\}\)
\(\mathcal{O}(n^2)\)
margin
Sparsefinder
1️⃣ Extract heads from a pre-trained \(\alpha\)-entmax transformer
2️⃣ Learn lower dimensionality projections
3️⃣ Group \(\langle\bm{q},\bm{k}\rangle\) and compute attention within groups
\mathcal{L}_\theta(\mathcal{G}_h) = \Big[
\omega +
\|\bm{q}' - \bm{k}'_{\text{P}}\|^2_2 -
\|\bm{q}' - \bm{k}'_{\text{N}}\|^2_2
\Big]_{+}
\(\bm{q}' = \bm{W}^Q_h \bm{q}\)
\(\bm{k}' = \bm{W}^Q_h \bm{k}\)
negative pair
positive pair
distance-based
\(\hat{\mathcal{G}}_h = \{(\bm{q}_i, \bm{k}_j) \mid \|\bm{q}'_i - \bm{k}'_j\| \leq t\}\)
\(\mathcal{O}(n^2)\)
bucketing
quantize each \(1,...,r\) dim.
into \(\beta\) bins of size \(\lceil n/\beta\rceil\)
\(\mathcal{O}(n\sqrt{n})\)
margin
Sparsefinder
1️⃣ Extract heads from a pre-trained \(\alpha\)-entmax transformer
2️⃣ Learn lower dimensionality projections
3️⃣ Group \(\langle\bm{q},\bm{k}\rangle\) and compute attention within groups
\mathcal{L}_\theta(\mathcal{G}_h) = \Big[
\omega +
\|\bm{q}' - \bm{k}'_{\text{P}}\|^2_2 -
\|\bm{q}' - \bm{k}'_{\text{N}}\|^2_2
\Big]_{+}
\(\bm{q}' = \bm{W}^Q_h \bm{q}\)
\(\bm{k}' = \bm{W}^Q_h \bm{k}\)
negative pair
positive pair
distance-based
\(\hat{\mathcal{G}}_h = \{(\bm{q}_i, \bm{k}_j) \mid \|\bm{q}'_i - \bm{k}'_j\| \leq t\}\)
\(\mathcal{O}(n^2)\)
bucketing
quantize each \(1,...,r\) dim.
into \(\beta\) bins of size \(\lceil n/\beta\rceil\)
\(\mathcal{O}(n\sqrt{n})\)
clustering
learn centroids \({\bm{c}_1, ..., \bm{c}_B}\) and set points to closest cluster
\(\mathcal{O}(n\sqrt{n})\)
margin
Sparsefinder
1️⃣ Extract heads from a pre-trained \(\alpha\)-entmax transformer
2️⃣ Learn lower dimensionality projections
3️⃣ Group \(\langle\bm{q},\bm{k}\rangle\) and compute attention within groups
4️⃣ Add window and global patterns to \(\hat{\mathcal{G}}\)
\mathcal{L}_\theta(\mathcal{G}_h) = \Big[
\omega +
\|\bm{q}' - \bm{k}'_{\text{P}}\|^2_2 -
\|\bm{q}' - \bm{k}'_{\text{N}}\|^2_2
\Big]_{+}
\(\bm{q}' = \bm{W}^Q_h \bm{q}\)
\(\bm{k}' = \bm{W}^Q_h \bm{k}\)
negative pair
positive pair
distance-based
bucketing
clustering
margin
Sparse-consistency property
\(QK^\top\) scores
\(\alpha\)-entmax
\(\Bigg(\)
\(\Bigg)\)
||
\(\mathcal{G}\): \(\alpha\)-entmax attention graph
Sparse-consistency property
\(QK^\top\) scores
\(\alpha\)-entmax
\(\Bigg(\)
\(\Bigg)\)
||
\(\mathcal{G}\): \(\alpha\)-entmax attention graph
Sparse-consistency property
\(\alpha\)-entmax
\(\Bigg(\)
\(\Bigg)\)
\(\mathcal{G}\): \(\alpha\)-entmax attention graph
||
Sparse-consistency property
\(\alpha\)-entmax
\(\Bigg(\)
\(\Bigg)\)
\(\mathcal{G}\): \(\alpha\)-entmax attention graph
||
\(\mathcal{G}\): \(\alpha\)-entmax attention graph
Sparse-consistency property
\(\alpha\)-entmax
\(\Bigg(\)
\(\Bigg)\)
||
\(QK^\top\) scores
Sparse-consistency property
\(\alpha\)-entmax
\(\Bigg(\)
\(\Bigg)\)
||
\(\mathcal{G}\): \(\alpha\)-entmax attention graph
\(QK^\top\) scores
Sparse-consistency property
\(\alpha\)-entmax
\(\Bigg(\)
\(\Bigg)\)
||
\(\mathcal{G}\): \(\alpha\)-entmax attention graph
\(QK^\top\) scores
Sparse-consistency property
\(\alpha\)-entmax
\(\Bigg(\)
\(\Bigg)\)
||
\(\mathcal{G}\): \(\alpha\)-entmax attention graph
\(QK^\top\) scores
Experiments: Masked LM
• Distribution of part-of-speech tags on the validation set
- for each cluster
- for each head
Experiments: Masked LM
• Distribution of part-of-speech tags on the validation set
- for each cluster
- for each head
• verbs, nouns, auxiliary verbs attend to each other
Sparsefinder cost
\(N = \) sequence length
\(C = \) number of clusters
\(T = \lceil N / C \rceil \) (max-size of balanced clusters)
\(O(C \times T^2) = O(C \times N^2 / C^2) = O(N^2 / C)\)
If \(C = \sqrt{N}\), then
\(O(N^2 / C) = O(N\sqrt{N})\)
\(N = 20 \), \(C = 4 \), balanced clusters
Sparsefinder - SPNLP
By mtreviso
