The Explanation Game:

Towards Prediction Explainability through Sparse Communication

June 23, 2020

Marcos V. Treviso

André F. T. Martins

Motivations for Explainability
Definitions and Works on NLP
Explainability Techniques and Classic Feature Selection
Embedded Sparse Attention
Explainability as Communication
Experiments
Human Evaluation
Final Remarks

Agenda

Social Motivation: Critical Systems

Social Motivation: Critical Systems

Social Motivation: Critical Systems

Standard ML models have lower precision to detect pedestrians crossing the road if they have dark skin [Wilson et al., 2019]

Social Motivation: Criminal Justice

[ref]

Social Motivati

[ref]

on: Criminal Justice

Social Motivation: Imagine

Military
- Drones carrying explosives or weapons
Recruiting
- ML models to streamline the process

Healthcare
- Responsibility?
- Confidentiality?

Insights Motivation

The Deep Patient case (Miotto et al., 2016)
- 700,000 patients / 78 diseases
- DL model with high accuracy for several diseases

Electronic Health Records

[ref]

Insights Motivation

The Deep Patient case (Miotto et al., 2016)
- 700,000 patients / 78 diseases
- DL model with high accuracy for several diseases
- But doctors find very hard to antecipate schizophrenia

Electronic Health Records

[ref]

Design Motivation

One pixel attack
- Why?

(Su et al., 2019)

Design Motivation

One pixel attack
- Why?

Adversarial examples
- Why?

(Goodfellow et al., 2015)

Design Motivation

Husky vs Wolf task

Design Motivation

Husky vs Wolf task

[ref]

Design Motivation

Husky vs Wolf task

(Ribeiro et al., 2016)

Motivation: NLP

Explanations in NLP

(Ribeiro et al., 2016)

Motivation: NLP

Explanations in NLP

(Galassi et al., 2019)

Motivation: NLP

Explanations in NLP

(Strobelt et al., 2018)

Motivation: NLP

Explanations in NLP: Rationales
- "a short yet sufficient part of the input text"
  (Lei et al., 2016; Bastings et al., 2019)
- "snippets that support the output"
  (DeYoung et al., 2020)

(Lei et al., 2016)

(DeYoung et al., 2020)

Definitions

Source: xaitutorial2020.github.io

What is Trustable AI?
What is explainability? interpretability? transparency?
To whom we are trying to explain?
Explain the model or the decision for a particular input?

Definitions

What is Trustable AI?
What is explainability? interpretability? transparency?
To whom we are trying to explain?
Explain the model or the decision for a particular input?
Large body of work on analysis and interpretation of NNs!
See (Doshi-Velez and Kim, 2017; Lipton, 2018; Gilpin et al., 2018; Miller, 2019).
See AAAI 2020 Explainable AI Tutorial

Definitions

Attention is not explanation (Jain and Wallace, 2019)
- attention mappings vs gradient probing information

attention is uncorrelated with gradient-based measures
different attention weights yield equivalent predictions

Works on NLP

Attention is not explanation (Jain and Wallace, 2019)
- attention mappings vs gradient probing information
Is attention interpretable? (Serrano and Smith, 2019)
- attention ablation study, looking for decision shifts

attention is uncorrelated with gradient-based measures
different attention weights yield equivalent predictions

highest attention weights fail to have a large impact
need to erase a large set of att. weights to flip a decision

Works on NLP

Attention is not explanation (Jain and Wallace, 2019)
- attention mappings vs gradient probing information
Is attention interpretable? (Serrano and Smith, 2019)
- attention ablation study, looking for decision shifts

Works on NLP

attention is uncorrelated with gradient-based measures
different attention weights yield equivalent predictions

highest attention weights fail to have a large impact
need to erase a large set of att. weights to flip a decision

As a importance measure, it fails to explain model decisions

Attention is not not explanation (Wiegreffe and Pinter, 2019)
- questions the conclusions of the previous and proposes various explainability tests

Works on NLP

Attention is not not explanation (Wiegreffe and Pinter, 2019)
- questions the conclusions of the previous and proposes various explainability tests
How should we define and evaluate faithfulness? (Jacovi and Goldberg, 2020)
- Plausibility: how convincing the interpretation is to humans
- Faithfulness: how accurately it reflects the true reasoning process of the model

Works on NLP

Attention is not not explanation (Wiegreffe and Pinter, 2019)
- questions the conclusions of the previous and proposes various explainability tests
How should we define and evaluate faithfulness? (Jacovi and Goldberg, 2020)
- Plausibility: how convincing the interpretation is to humans
- Faithfulness: how accurately it reflects the true reasoning process of the model
- Graded notion of faithfulness

Works on NLP

Rationalizer models
- Arguably more faithful
Classifier $f_\theta$ that, given latent
masks $z$ and $x$ as input, output $y$

Works on NLP

(Bastings et al., 2019)

Z_i | X \sim \mathrm{Bernoulli}(g_i(x; \phi))

Y | x, z \sim \mathrm{Cat}(f(x \odot z; \theta))

Rationale extractor $g_\phi$ that generates masks $z$

Z_i | X \sim \mathrm{HardKuma}(g_i(x; \phi))

(Bastings et al., 2019)

(Lei et al., 2016)

Rationalizer models
- Arguably more faithful
Stochastic gradients
- Reinforce
- Reparameterization trick
Encourage sparsity and contiguity directly in the loss fn

Works on NLP

\min\limits_{\theta,\phi} - \underbrace{\mathcal{L}(\theta, \phi)}_{} + \underbrace{\lambda_0 \sum_i z_i}_{} + \underbrace{\lambda_1 \sum_i |z_i - z_{i+1}|}_{}

sparse

rationales

contiguous rationales

(Bastings et al., 2019)

class. loss

Comprehensive vs sufficient rationales (DeYoung et al., 2020)
- Com. have all necessary information to make a decision
- Suf. have enough information to make a decision

Works on NLP

Forest

Classical feature selection
- Happens statically at run time
- After training, irrelevant features
  are permanently deleted from the model

Revisiting Feature Selection

Classical feature selection
- Happens statically at run time
- After training, irrelevant features
  are permanently deleted from the model

Prediction explainability
- Happens dynamically at run time
- A feature not relevant for a particular
  input can be relevant for another

Revisiting Feature Selection

Typology (Guyon and Elisseeff, 2003)

Revisiting Feature Selection

Wrappers: “utilize the learning machine of interest as a black box to score subsets of variable according to their predictive power” (e.g. forward selection)

Filters: decide to include/exclude a feature based on an importance metric (e.g. pairwise mutual information)

Embedded: embed feature selection within the learning algorithm by using a sparse regularizer
(e.g. ℓ1-norm)

Static: feature selector & learning algorithm
Dynamic: explainer & classifier

Revisiting Feature Selection

	static	dynamic
wrapper	Forward selection Backward elimination	Representation erasure Leave one out LIME

Static: feature selector & learning algorithm
Dynamic: explainer & classifier

Revisiting Feature Selection

	static	dynamic
wrapper	Forward selection Backward elimination	Representation erasure Leave one out LIME
filter	Pointwise mutual information Recursive feature elimination	Input gradient Top-k attention

Static: feature selector & learning algorithm
Dynamic: explainer & classifier

Revisiting Feature Selection

	static	dynamic
wrapper	Forward selection Backward elimination	Representation erasure Leave one out LIME
filter	Pointwise mutual information Recursive feature elimination	Input gradient Top-k attention
embedded	ℓ1-regularization elastic net	Stochastic attention Sparse attention

Attention

query keys values

$$\mathbf{q} \in \mathbb{R}^{ d_q}$$

$$\mathbf{K} \in \mathbb{R}^{n \times d_k}$$

$$\mathbf{V} \in \mathbb{R}^{n \times d_v}$$

1. Compute a score between q and each kj

$$\mathbf{s} = \mathrm{score}(\mathbf{q}, \mathbf{K}) \in \mathbb{R}^{n} $$

2. Map scores to probabilities

$$\mathbf{p} = \pi(\mathbf{s}) \in \triangle^{n} $$

Attention

query keys values

$$\mathbf{q} \in \mathbb{R}^{ d_q}$$

$$\mathbf{K} \in \mathbb{R}^{n \times d_k}$$

$$\mathbf{V} \in \mathbb{R}^{n \times d_v}$$

1. Compute a score between q and each kj

$$\mathbf{s} = \mathrm{score}(\mathbf{q}, \mathbf{K}) \in \mathbb{R}^{n} $$

2. Map scores to probabilities

$$\mathbf{p} = \pi(\mathbf{s}) \in \triangle^{n} $$

(Niculae , 2018)

$$ \exp(\mathbf{s}_j) / \sum_k \exp(\mathbf{s}_k) $$

softmax:

Attention

query keys values

$$\mathbf{q} \in \mathbb{R}^{ d_q}$$

$$\mathbf{K} \in \mathbb{R}^{n \times d_k}$$

$$\mathbf{V} \in \mathbb{R}^{n \times d_v}$$

1. Compute a score between q and each kj

$$\mathbf{s} = \mathrm{score}(\mathbf{q}, \mathbf{K}) \in \mathbb{R}^{n} $$

2. Map scores to probabilities

$$\mathbf{p} = \pi(\mathbf{s}) \in \triangle^{n} $$

$$ \exp(\mathbf{s}_j) / \sum_k \exp(\mathbf{s}_k) $$

Dense

Less faithful

Not an embedded method!

softmax:

Attention

query keys values

$$\mathbf{q} \in \mathbb{R}^{ d_q}$$

$$\mathbf{K} \in \mathbb{R}^{n \times d_k}$$

$$\mathbf{V} \in \mathbb{R}^{n \times d_v}$$

1. Compute a score between q and each kj

$$\mathbf{s} = \mathrm{score}(\mathbf{q}, \mathbf{K}) \in \mathbb{R}^{n} $$

2. Map scores to probabilities

$$\mathbf{p} = \pi(\mathbf{s}) \in \triangle^{n} $$

$$ \mathrm{argmin}_{\mathbf{p} \in \triangle^n} \,||\mathbf{p} - \mathbf{s}||_2^2 $$

sparsemax:

(Niculae , 2018)

Attention

query keys values

$$\mathbf{q} \in \mathbb{R}^{ d_q}$$

$$\mathbf{K} \in \mathbb{R}^{n \times d_k}$$

$$\mathbf{V} \in \mathbb{R}^{n \times d_v}$$

1. Compute a score between q and each kj

$$\mathbf{s} = \mathrm{score}(\mathbf{q}, \mathbf{K}) \in \mathbb{R}^{n} $$

2. Map scores to probabilities

$$\mathbf{p} = \pi(\mathbf{s}) \in \triangle^{n} $$

$$ \mathrm{argmin}_{\mathbf{p} \in \triangle^n} \,||\mathbf{p} - \mathbf{s}||_2^2 $$

sparsemax:

Sparse

More faithful

An embedded method!

Sparse Attention

More generally
- α-entmax transformation (Peters et al., 2019):

\begin{cases} \frac{1}{\alpha(\alpha-1)}\sum_j(p_j-p_j^\alpha), & \alpha \neq 1\\ -\sum_j p_j \log p_j, & \alpha=1. \end{cases}

\alpha\text{-entmax}(\mathbf{s}) := \argmax_{\mathbf{p} \in \triangle^{n}} \mathbf{p}^\top \mathbf{s} + H_\alpha(\mathbf{p})

\Bigg\{

Tsallis α-entropy regularizer

(Peters et al. , 2019)

Explainability as Communication

Ability of an explainer to communicate the rationale of a decision in terms that can be understood by a human
+ success of communication + plausability
Human-grounded evaluation through forward simulation/prediction (Doshi-Velez and Kim, 2017, §3.2)

Communication Framework

Classifier $C$
- $\hat{y} = C(x) \approx y$
- hidden representations $h$
Explainer $E$
- $m = E(x, \hat{y}, h)$
- $m \in \mathcal{M}$ is regarded as a “rationale” for $\hat{y}$
Layperson $L$
- $\tilde{y} = L(m)$
- simple model (e.g., a linear classifier)

Communication Framework

Classifier

Explainer

Layperson

$\hat{y} = C(x)$

$m = E(x, \hat{y}, h) \in \mathcal{M} $

$\tilde{y} = L(m)$

The communication is successful if $\hat{y} = \tilde{y}$

Communication Framework

Classifier

Explainer

Layperson

$\hat{y} = C(x)$

$m = E(x, \hat{y}, h) \in \mathcal{M} $

$\tilde{y} = L(m)$

The communication is successful if $\hat{y} = \tilde{y}$
Communication Success Rate (CSR)
A quantifiable measure of explainability
$\uparrow$ CSR $\implies$ informative messages

\mathrm{CSR} = \frac{1}{N}\sum_{n=1}^N \big[\big[{\hat{y}_n = \tilde{y}_n}\big]\big]

Communication Framework

Relation to filters and wrappers:
- $C$ and $E$ are separate components
- $E$ works as a post-hoc explainer
Relation to embedded methods:
- $E$ is embedded as an internal component of $C$
- e.g. rationalizer models and sparse attention

Classifier

Explainer

Layperson

$\hat{y} = C(x)$

$m = E(x, \hat{y}, h) \in \mathcal{M} $

$\tilde{y} = L(m)$

Communication Framework

Relation to filters and wrappers:
- $C$ and $E$ are separate components
- $E$ works as a post-hoc explainer
Relation to embedded methods:
- $E$ is embedded as an internal component of $C$
- e.g. rationalizer models and sparse attention

Possible messages?

Possible explainers?

Classifier

Explainer

Layperson

$\hat{y} = C(x)$

$m = E(x, \hat{y}, h) \in \mathcal{M} $

$\tilde{y} = L(m)$

Comm. Framework: Messages

Rationales
- BoW
- Word embeddings

Comm. Framework: Messages

Rationales
- BoW
- Word embeddings
Prototypes
Criticisms
...

Comm. Framework: Explainers

Wrappers
- LIME
- Leave one out
- Erasure
Filters
- Gradient-based
- Top-k attention
Embedded
- Stochastic attention
- Sparse attention

Comm. Framework: Explainers

Wrappers
- LIME
- Leave one out
- Erasure
Filters
- Gradient-based
- Top-k attention
Embedded
- Stochastic attention
- Sparse attention

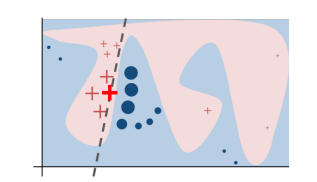
Perturbation method
Areas = complex decision boundaries
Bold red cross = instance we want to explain

Comm. Framework: Explainers

Wrappers
- LIME
- Leave one out
- Erasure
Filters
- Gradient-based
- Top-k attention
Embedded
- Stochastic attention
- Sparse attention

why this movie is so bad ?

90%

80%

why      movie is so bad ?

89%

why this movie is so     ?

58%

    this movie is so bad ?

Comm. Framework: Explainers

Wrappers
- LIME
- Leave one out
- Erasure
Filters
- Gradient-based
- Top-k attention
Embedded
- Stochastic attention
- Sparse attention

why this movie is so bad ?

measure

(grad/attn)

why this movie is so bad ?

why this movie is so ?

why this movie is so ?

this movie is so ?

Comm. Framework: Explainers

Wrappers
- LIME
- Leave one out
- Erasure
Filters
- Gradient-based
- Top-k attention
Embedded
- Stochastic attention
- Sparse attention

why this movie is so bad ?

measure

(grad/attn)

why this movie is so bad ?

why bad ?

top k

Comm. Framework: Explainers

Wrappers
- LIME
- Leave one out
- Erasure
Filters
- Gradient-based
- Top-k attention
Embedded
- Stochastic attention
- Sparse attention

why this movie is so bad ?

measure

(grad/attn)

why movie bad ?

why this movie is so bad ?

Comm. Framework: Explainers

Wrappers
- LIME
- Leave one out
- Erasure
Filters
- Gradient-based
- Top-k attention
Embedded
- Stochastic attention
- Sparse attention

Humans

Comm. Framework: Explainers

So far
- $E$ queries $C$ multiple times
- Or $E$ is embedded in $C$ and we access $m$
But
- $E$ can be seen as a separate trainable model!

Comm. Framework: Explainers

So far
- $E$ queries $C$ multiple times
- Or $E$ is embedded in $C$ and we access $m$
But
- $E$ can be seen as a separate trainable model!

Comm. Framework: Explainers

Joint training of $E$ and $L$
- Cooperative game
- Maximize CSR
Let $E_\theta$ and $L_\phi$, and input $(x, \hat{y})$
Multitask objective
- Reconstruction term: $\mathcal{L}(\phi, \theta) = -\log p_\phi(\hat{y} \mid m)$
- Faithfulness term: $\Omega(\theta) = \|\tilde{h}(E_{\theta}), h\|^2$
  
  $\mathcal{L}_{\Omega}(\phi, \theta) := \mathcal{L}(\phi, \theta) + \lambda \Omega(\theta)$

C's hidden reps.

E's predictions of h reps.

C's predictions are passed as input to E

message

Comm. Framework: Explainers

Joint training of $E$ and $L$
- Cooperative game
- Maximize CSR
Let $E_\theta$ and $L_\phi$, and input $(x, \hat{y})$
Multitask objective
- Reconstruction term: $\mathcal{L}(\phi, \theta) = -\log p_\phi(\hat{y} \mid m)$
- Faithfulness term: $\Omega(\theta) = \|\tilde{h}(E_{\theta}), h\|^2$
  
  $\mathcal{L}_{\Omega}(\phi, \theta) := \mathcal{L}(\phi, \theta) + \lambda \Omega(\theta)$

C's hidden reps.

E's predictions of h reps.

C's predictions are passed as input to E

message

Comm. Framework: Explainers

Trivial protocol

why this movie is so bad ?

$L$

I think this is a good film

$L$

Heuristics to avoid it
- Forbid stop words from being selected by $E$
- $E$ will access $\hat{y}$ with a chance of $\beta$ (e.g. $\beta=20\%$)

iter

$\beta$

20%

End of training

Experiments

Classifier $C$
1. Embedding
2. BiLSTM
3. Additive attention with $\alpha \in \{1.0, \, 1.5, \, 2.0\}$
4. Linear output
Explainer $E$
- $m$ = BoWs
Layperson $L$
- Linear

softmax

1.5-entmax

sparsemax

Experiments

IMDB

BoW

$C_{soft}$

$C_{sparse}$

$C_{ent}$

$C_{bern}$

$C_{hk}$

92%
90%
88%
86%

SNLI

BoW

$C_{soft}$

$C_{sparse}$

$C_{ent}$

$C_{bern}$

$C_{hk}$

84%

80%
76%
72%
68%

Classifier results (accuracy)

Experiments

Communication results (CSR)

IMDB

Random

Erasure

Top-k

ent

Top-k soft

95% 93% 91% 89% 87% 85%

68%

Top-k

sparse

Select.

ent

Select.

sparse

Bernoulli

HardKuma

$C_{soft}$

$C_{sparse}$

$C_{ent}$

$C_{bern}$

$C_{hk}$

$C_{soft}$

$C_{ent}$

$C_{sparse}$

Top-k Gradient

$C_{soft}$

Random

Erasure

Top-k

ent

Top-k soft

83% 81% 79% 77% 75%

Top-k

sparse

Select.

ent

Select.

sparse

Bernoulli

HardKuma

$C_{soft}$

$C_{sparse}$

$C_{ent}$

$C_{bern}$

$C_{hk}$

$C_{soft}$

$C_{ent}$

$C_{sparse}$

$C_{soft}$

SNLI

Top-k Gradient

Experiments

Communication results (CSR)

IMDB

Random

Erasure

Top-k

ent

Top-k soft

95% 93% 91% 89% 87% 85%

68%

Top-k

sparse

Select.

ent

Select.

sparse

Bernoulli

HardKuma

$C_{soft}$

$C_{sparse}$

$C_{ent}$

$C_{bern}$

$C_{hk}$

$C_{soft}$

$C_{ent}$

$C_{sparse}$

Top-k Gradient

$C_{soft}$

Random

Erasure

Top-k

ent

Top-k soft

83% 81% 79% 77% 75%

Top-k

sparse

Select.

ent

Select.

sparse

Bernoulli

HardKuma

$C_{soft}$

$C_{sparse}$

$C_{ent}$

$C_{bern}$

$C_{hk}$

$C_{soft}$

$C_{ent}$

$C_{sparse}$

$C_{soft}$

SNLI

Top-k Gradient

Experiments

Communication results (CSR)

IMDB

Random

Erasure

Top-k

ent

Top-k soft

95% 93% 91% 89% 87% 85%

68%

Top-k

sparse

Select.

ent

Select.

sparse

Bernoulli

HardKuma

$C_{soft}$

$C_{sparse}$

$C_{ent}$

$C_{bern}$

$C_{hk}$

$C_{soft}$

$C_{ent}$

$C_{sparse}$

Top-k Gradient

$C_{soft}$

Random

Erasure

Top-k

ent

Top-k soft

83% 81% 79% 77% 75%

Top-k

sparse

Select.

ent

Select.

sparse

Bernoulli

HardKuma

$C_{soft}$

$C_{sparse}$

$C_{ent}$

$C_{bern}$

$C_{hk}$

$C_{soft}$

$C_{ent}$

$C_{sparse}$

$C_{soft}$

SNLI

Top-k Gradient

Experiments

Communication results (accuracy of $L$)

IMDB

Random

Erasure

Top-k

ent

Top-k soft

95% 93% 91% 89% 87% 85%

68%

Top-k

sparse

Select.

ent

Select.

sparse

Bernoulli

HardKuma

$C_{soft}$

$C_{sparse}$

$C_{ent}$

$C_{bern}$

$C_{hk}$

$C_{soft}$

$C_{ent}$

$C_{sparse}$

$C_{soft}$

Random

Erasure

Top-k

ent

Top-k soft

75%

73%

71%

69%

67%

Top-k

sparse

Select.

ent

Select.

sparse

Bernoulli

HardKuma

$C_{soft}$

$C_{sparse}$

$C_{ent}$

$C_{bern}$

$C_{hk}$

$C_{soft}$

$C_{ent}$

$C_{sparse}$

$C_{soft}$

SNLI

Top-k Gradient

Experiments

Communication results (accuracy of $L$)

IMDB

Random

Erasure

Top-k

ent

Top-k soft

95% 93% 91% 89% 87% 85%

68%

Top-k

sparse

Select.

ent

Select.

sparse

Bernoulli

HardKuma

$C_{soft}$

$C_{sparse}$

$C_{ent}$

$C_{bern}$

$C_{hk}$

$C_{soft}$

$C_{ent}$

$C_{sparse}$

$C_{soft}$

Random

Erasure

Top-k

ent

Top-k soft

75%

73%

71%

69%

67%

Top-k

sparse

Select.

ent

Select.

sparse

Bernoulli

HardKuma

$C_{soft}$

$C_{sparse}$

$C_{ent}$

$C_{bern}$

$C_{hk}$

$C_{soft}$

$C_{ent}$

$C_{sparse}$

$C_{soft}$

SNLI

Top-k Gradient

Experiments

Communication results (accuracy of $L$)

IMDB

Random

Erasure

Top-k

ent

Top-k soft

95% 93% 91% 89% 87% 85%

68%

Top-k

sparse

Select.

ent

Select.

sparse

Bernoulli

HardKuma

$C_{soft}$

$C_{sparse}$

$C_{ent}$

$C_{bern}$

$C_{hk}$

$C_{soft}$

$C_{ent}$

$C_{sparse}$

$C_{soft}$

Random

Erasure

Top-k

ent

Top-k soft

75%

73%

71%

69%

67%

Top-k

sparse

Select.

ent

Select.

sparse

Bernoulli

HardKuma

$C_{soft}$

$C_{sparse}$

$C_{ent}$

$C_{bern}$

$C_{hk}$

$C_{soft}$

$C_{ent}$

$C_{sparse}$

$C_{soft}$

SNLI

Top-k Gradient

Experiments

Impact of the sparsity (length of the message)

IMDB

SNLI

emb. 1.5-entmax

emb. sparsemax

text length

emb. sparsemax

emb. 1.5-entmax

text length

Experiments

Impact of the sparsity (length of the message)

CSR does not increase monotonically with k

IMDB

SNLI

Experiments

Impact of the sparsity (length of the message)

IWSLT

$k$

Human Evaluation

Joint $E$ and $L$ model
- Maximize the communication
Human $L$
- 200 random examples
- Explanations shuffled
Human $E$
- e-SNLI corpus
- Human highlights
  (nonneutral pairs only)
- CSR = ACC always

Human Evaluation

Human Evaluation

Human Evaluation

Human Evaluation

Human Evaluation

Human Evaluation

Final Remarks

A unified framework that regards explainability as a communication problem
- Flexibility between $C$, $E$ and $L$
- A link between classical feature selection and expl. methods
- Embedded method based on selective sparse attention
- Post-hoc explainer that is trained to optimize CSR

Final Remarks

A unified framework that regards explainability as a communication problem
- Flexibility between $C$, $E$ and $L$
- A link between classical feature selection and expl. methods
- Embedded method based on selective sparse attention
- Post-hoc explainer that is trained to optimize CSR
Attention and erasure get higher CSR than gradient
Embedded selective attention is effective while being simpler to train than rationalizers

Refs

Benjamin Wilson, Judy Hoffman, and Jamie Morgenstern. Predictive inequity in object detection. arXiv preprint arXiv:1902.11097, 2019
Riccardo Miotto, Li Li, Brian A Kidd, and Joel T Dudley. Deep patient: an unsupervised representation to predict the future of patients from the electronic health records.Scientific reports, 6:26094, 2016
Su, Jiawei, Danilo Vasconcellos Vargas, and Kouichi Sakurai. "One pixel attack for fooling deep neural networks." IEEE Transactions on Evolutionary Computation 23.5 (2019): 828-841
Goodfellow, Ian J., Jonathon Shlens, and Christian Szegedy. "Explaining and harnessing adversarial examples." arXiv preprint arXiv:1412.6572 (2014)
Marco Tulio Ribeiro, Sameer Singh, and Carlos Guestrin. Why should i trust you? Explaining the predictions of any classifier. In Proceedings of the 22nd ACMSIGKDD international conference on knowledge discovery and data mining, pages 1135–1144. ACM, 2016

Refs

Strobelt, Hendrik, et al. "Seq 2seq-vis: A visual debugging tool for sequence-to-sequence models." IEEE transactions on visualization and computer graphics 25.1 (2018): 353-363.
Galassi, Andrea, Marco Lippi, and Paolo Torroni. "Attention in Natural Language Processing." 2019. Arxiv 1902.02181
Niculae, Vlad. "Learning Deep Models with Linguistically-Inspired Structure." (2018).

Ben Peters, Vlad Niculae, and Andre FT Martins. 2019. Sparse sequence-to-sequence models. Proc. ACL.
Goncalo M Correia, Vlad Niculae, and Andre FT Martins. 2019. Adaptively sparse transformers. In Proc. EMNLP-IJCNLP, pages 2174–2184.
Joost Bastings, Wilker Aziz, and Ivan Titov. 2019. Interpretable neural predictions with differentiable binary variables. In Proc. ACL.

Refs

Jay DeYoung, Sarthak Jain, Nazneen Fatema Rajani, Eric Lehman, Caiming Xiong, Richard Socher, and Byron C Wallace. 2020. Eraser: A benchmark to evaluate rationalized nlp models. arXiv preprint arXiv:1911.03429.
Leilani H Gilpin, David Bau, Ben Z Yuan, Ayesha Bajwa, Michael Specter, and Lalana Kagal. 2018. Explaining explanations: An overview of interpretability of machine learning. In Proc. DSAA, pages 80–89.
Alon Jacovi and Yoav Goldberg. 2020. Towards faithfully interpretable nlp systems: How should we define and evaluate faithfulness? In Proc. of ACL.
Sarthak Jain and Byron C Wallace. 2019. Attention is not explanation. In Proc. NAACL-HLT.
Tao Lei, Regina Barzilay, and Tommi Jaakkola. 2016. Rationalizing neural predictions. In Proc. EMNLP, pages 107–117.
Zachary C. Lipton. 2018. The mythos of model interpretability. Commun. ACM, 61(10):36–43.

Refs

Tim Miller. 2019. Explanation in artificial intelligence: Insights from the social sciences. Artificial Intelligence, 267:1–38.
Cynthia Rudin. 2019. Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nature Machine Intelligence, 1(5):206–215.
Sofia Serrano and Noah A Smith. 2019. Is attention interpretable? In Proc. ACL.
Sarah Wiegreffe and Yuval Pinter. 2019. Attention is not not explanation. In Proc. EMNLP-IJCNLP.
Mo Yu, Shiyu Chang, Yang Zhang, and Tommi Jaakkola. 2019. Rethinking cooperative rationalization: Introspective extraction and complement control. InProc. EMNLP-IJCNLP, pages 4085–4094.

Thank you for your attention!

marcos.treviso@tecnico.ulisboa.pt

Social Motivation: Critical Systems

Motivation: NLP

Explanations in NLP: Rationales

(DeYoung et al., 2020)

Definitions

Source: xaitutorial2020.github.io

What is Trustable AI?
What is explainability? interpretability? transparency?
To whom we are trying to explain?
Explain the model or the decision for a particular input?
Large body of work on analysis and interpretation of NNs!
See (Doshi-Velez and Kim, 2017; Lipton, 2018; Gilpin et al., 2018; Miller, 2019).
See AAAI 2020 Explainable AI Tutorial

Definitions

It's easier to poke holes in a study than to run one yourself.

COVID-19 Data Dives: The Takeaways From Seroprevalence Surveys.
Natalie E. Dean. May/2020. Medscape

Human Evaluation

the-explanation-game

By mtreviso