Ergodicity in Principle and in Practice
Nicolas Underwood
and Fabien Paillusson
Towards a widely applicable, spectral notion of ergodicity



(In case of YouTube/Zoom/etc compression damaging quality of animations, slides available at slides.com/n_underwood/ee2023)
$$\overbrace{\lim_{T\rightarrow\infty}\int_0^T f\left(x(x_i,t,z)\right)\mathrm{d}t}^{\text{time/trajectory mean of }f}=\overbrace{\int_\Omega f(x)\mu(x)dx}^{\text{ensemble mean of }f}.$$
Birkhoff's equation
- However Boltzmann introduced the notion of ergodicity in the kinetic theory of gases as a property of the dynamics that justified statistical laws.
- In the historical notion(s) of ergodicity, the equality of averages is a consequence of ergodicity.
These days it is common to use the word ergodic to refer to the equality of time and ensemble averages of an observable or phase/state function \(f(x)\),
\(x\): generalized "state space" coordinates
\(\mu(x)\) : The measure (ensemble members per unit volume measured in coords \(x\))
\(f(x)\): the observable/phase function evaluated at coords \(x\)
\(z\): random numbers (if a stochastic system)
\(t\): time elapsed along trajectory
\(x_i\): initial state
\(T\): total time elapsed along trajectory
\(\int\) or \(\sum\): sum or integral over time
\(\int\) or \(\sum\): sum or integral over ensemble
\(\Omega\)
\(f(x)\)
Boltzmann's original notion
Intuition
A trajectory eventually passes through (samples) every state (on a constant energy surface).
Problem
A one-dimensional trajectory cannot "fill" an n-dimensional space. Boltzmann appears to have taken a discrete view of states on the surface.

Selected notions of ergodicity

Birkhoff

von Neumann

Tatyana
Afanasyeva

Paul Ehrenfest

Khinchin

Boltzmann
| Author | Name | Context | Notes |
|---|---|---|---|
| Ludwig Boltzmann (1884) | Ergodic hypothesis | Kinetic theory of gases | Original notion |
| Paul and Tatiana Ehrenfest (1911) | Quasi-Ergodic Hypothesis | Hamiltonian mechanics | "Almost all" initial points result in a trajectory that densely covers the phase space |
| George David Birkhoff (1931) | Pointwise Ergodic Theorem | Measure-preserving dynamical systems | Theorem I) Existence of infinite time average, Theorem II) Metric Transitivity (MT) implies equality of averages |
| John Von Neumann (1932) | Mean Ergodic Theorem | Hilbert spaces | Developed in tandem with and bares a resemblance to Birkhoff's results |
| Aleksandr Khinchin (1949) | Self-Similarity Argument | Hamiltonian mechanics | Requires large, highly separable system and limited to "sum functions" (limited applications) |
Over the years there have been various attempts to pin down Boltzmann's notion of ergodicity in a mathematically rigorous way, with the modern mathematical discipline of "Ergodic Theory" being based on Birkhoff's metric transitivity.
\(\Omega\)
\(f(x)\)
Metric transitivity
We consider co-moving volumes \(\omega(t)\subset\Omega\)
In measure preserving dynamics the co-moving volume remains of constant size, $$\mu(\omega(t)) = \mu(\omega(t_0)),$$
which is Liouville's theorem in Hamiltonian mechanics.
Invariant Volumes
An invariant volume \(\omega_\text{inv}\) is unchanged by the dynamics,
$$\omega_\text{inv}(t) = \omega_\text{inv}(t_0).$$
Metrically Indecomposable Invariant Volume
A metrically indecomposable (MI) volume, \(\omega_\text{MI}\), is a invariant volume that cannot be decomposed into two smaller invariant volumes,
$$\omega_\text{MI}\neq \omega_\text{1,inv}+\omega_\text{2,inv}.$$
Metrically transitivity (MT/ergodicity)
A system is metrically transitive (ergodic) if the only indecomposable invariant volumes satisfy
$$\mu(\omega_\text{inv})=\mu(\Omega)\text{ or }\mu(\omega_\text{inv})=0.$$
Birkhoff's theorem (II)
MT (ergodicity) \(\implies\) equality of averages.

$$\omega(t_0)\subseteq\Omega$$
\(\Omega\)
\(f(x)\)
Metric transitivity
We consider co-moving volumes \(\omega(t)\subset\Omega\)

In measure preserving dynamics the co-moving volume remains of constant size, $$\mu(\omega(t)) = \mu(\omega(t_0)),$$
which is Liouville's theorem in Hamiltonian mechanics.
Invariant Volumes
An invariant volume \(\omega_\text{inv}\) is unchanged by the dynamics,
$$\omega_\text{inv}(t) = \omega_\text{inv}(t_0).$$
Metrically Indecomposable Invariant Volume
A metrically indecomposable (MI) volume, \(\omega_\text{MI}\), is a invariant volume that cannot be decomposed into two smaller invariant volumes,
$$\omega_\text{MI}\neq \omega_\text{1,inv}+\omega_\text{2,inv}.$$
Metrically transitivity (MT/ergodicity)
A system is metrically transitive (ergodic) if the only indecomposable invariant volumes satisfy
$$\mu(\omega_\text{inv})=\mu(\Omega)\text{ or }\mu(\omega_\text{inv})=0.$$
Birkhoff's theorem (II)
MT (ergodicity) \(\implies\) equality of averages.
\(\Omega\)
\(f(x)\)
Metric transitivity
Consider union of co-moving volumes
$$\bigcup_{t=t_0}^\infty\omega(t)\subseteq\Omega$$
Equivalent (i think more) intuitive condition to MT
For every volume \(\omega(t_0)\) with \(\mu(\omega(t_0))>0\),
$$\mu\left(\bigcup_{t=t_0}^\infty\omega(t)\right)=\mu(\Omega),$$
so that every finite co-moving volume eventually fills the whole space.

$$\omega(t_0)\subseteq\Omega$$
\(\Omega\)
\(f(x)\)
Metric transitivity

Consider union of co-moving volumes
$$\bigcup_{t=t_0}^\infty\omega(t)\subseteq\Omega$$
Equivalent (i think more) intuitive condition to MT
For every volume \(\omega(t_0)\) with \(\mu(\omega(t_0))>0\),
$$\mu\left(\bigcup_{t=t_0}^\infty\omega(t)\right)=\mu(\Omega),$$
so that every finite co-moving volume eventually fills the whole space.
Relies on infinite time limit (the appropriateness of which is very context dependent).
Simple binary notion means no quantification of degree of non-ergodicity, or how commonly we may expect trajectories to violate equality of averages.
Non-MT systems may still be for all practical purposes ergodic (in the sense that statistical laws may still applyin practical circumstances).
In most cases, it is very difficult to prove.
Unlikely to be satisfied by many systems of interest across the natural and social sciences.
May be unnecessarily strong a condition for ergodicity in the sense of the equality of averages.
Issues with MT in a practical context:
Metric Transitivity is a rigorously defined notion of ergodicity that captures the essence of Boltzmann's ergodic hypothesis. So much so, that in Ergodic Theory, it is held as the definition of ergodicity. However...
\(\Omega\)
\(f(x)\)
Analysis of distributions
- In a practical experimental or numerical circumstance, any assessment of the agreement of ensemble and trajectory averages will involve collecting a set of function values collected over a trajectory with a set of values collected over an ensemble.
- However, a trajectory that is ergodic in the sense of Boltzmann won't simply experience a function average that is the same as the ensemble average. It will sample the same underlying distribution of values as the ensemble.
- So, using the same set of data used to compare averages, we may get closer to Boltzmann's ergodicity by comparing distributions.

Analysis of distributions
We have been developing an analysis based upon the comparison of trajectory and ensemble distributions.
- Based upon the Kolmogorov-Smirnov (KS) distance, a scalar measure between 0 and 1 that is used to quantify the difference between two distributions.
- Traditionally this is used to test whether two samples are drawn from the same underlying unknown(!) distribution.
- Such a test has for instance been used by one of us to prove non-ergodicity in Paillusson & Frenkel, Phys. Rev. Lett. 109, 208001 (2012)
- Currently however, we are considering to what extent the KS-distance provides a (non-binary) measure of (non-)ergodicity.
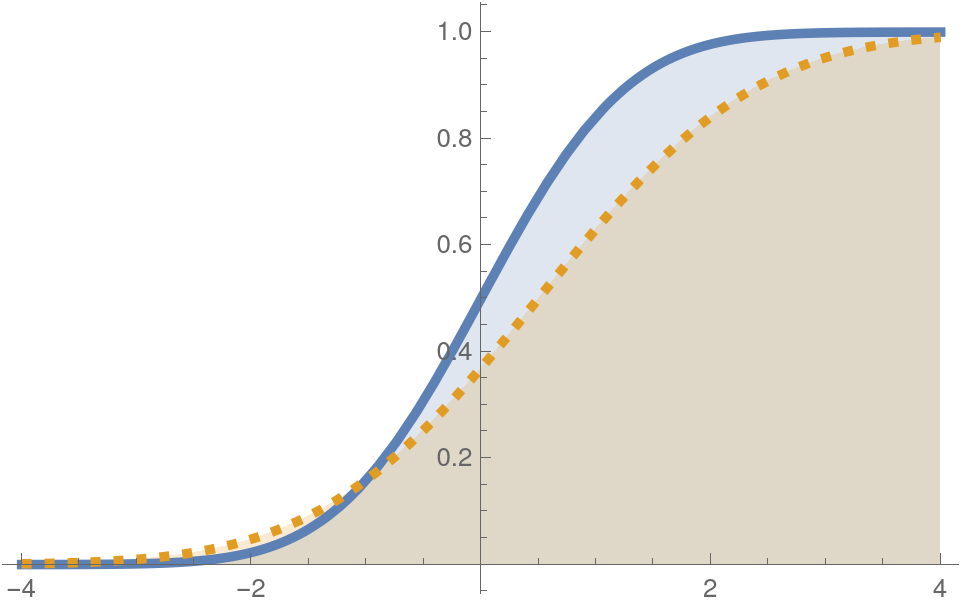
The KS-distance is the maximum vertical distance between two cumulative distribution functions (CDFs)
KS-distance
0
1
Values close to zero correspond to highly ergodic behaviour
Values close to one correspond to highly
non-ergodic behaviour
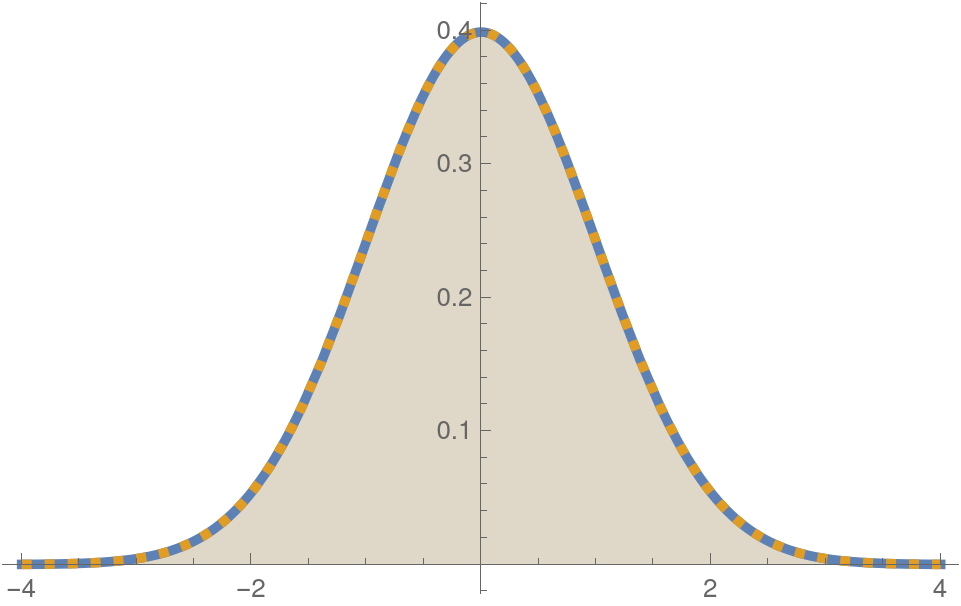
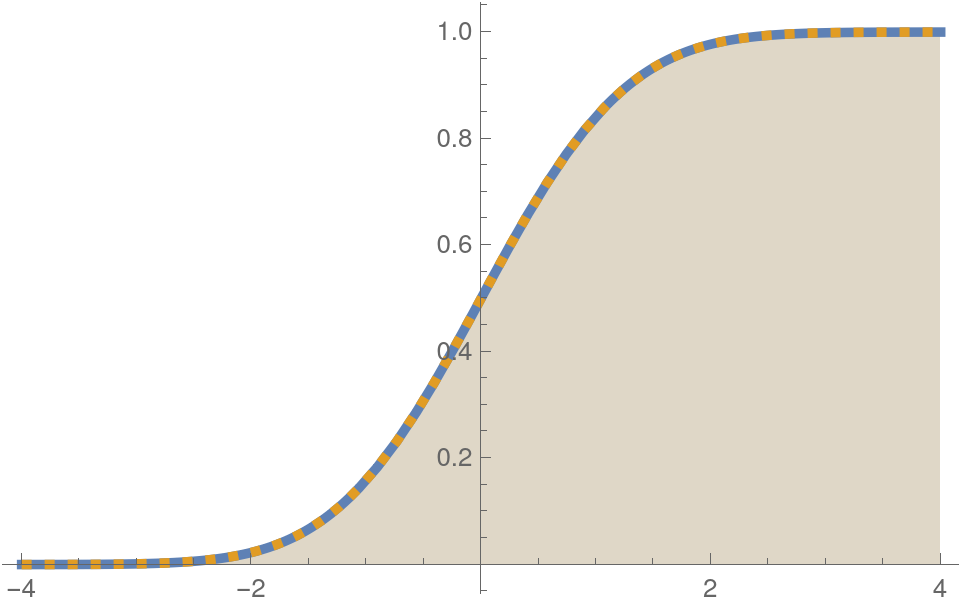
Convergence of numerical estimates of KS-distance to zero for identical distributions
Convergence of numerical estimates of KS-distance to a non-zero value for differing distributions
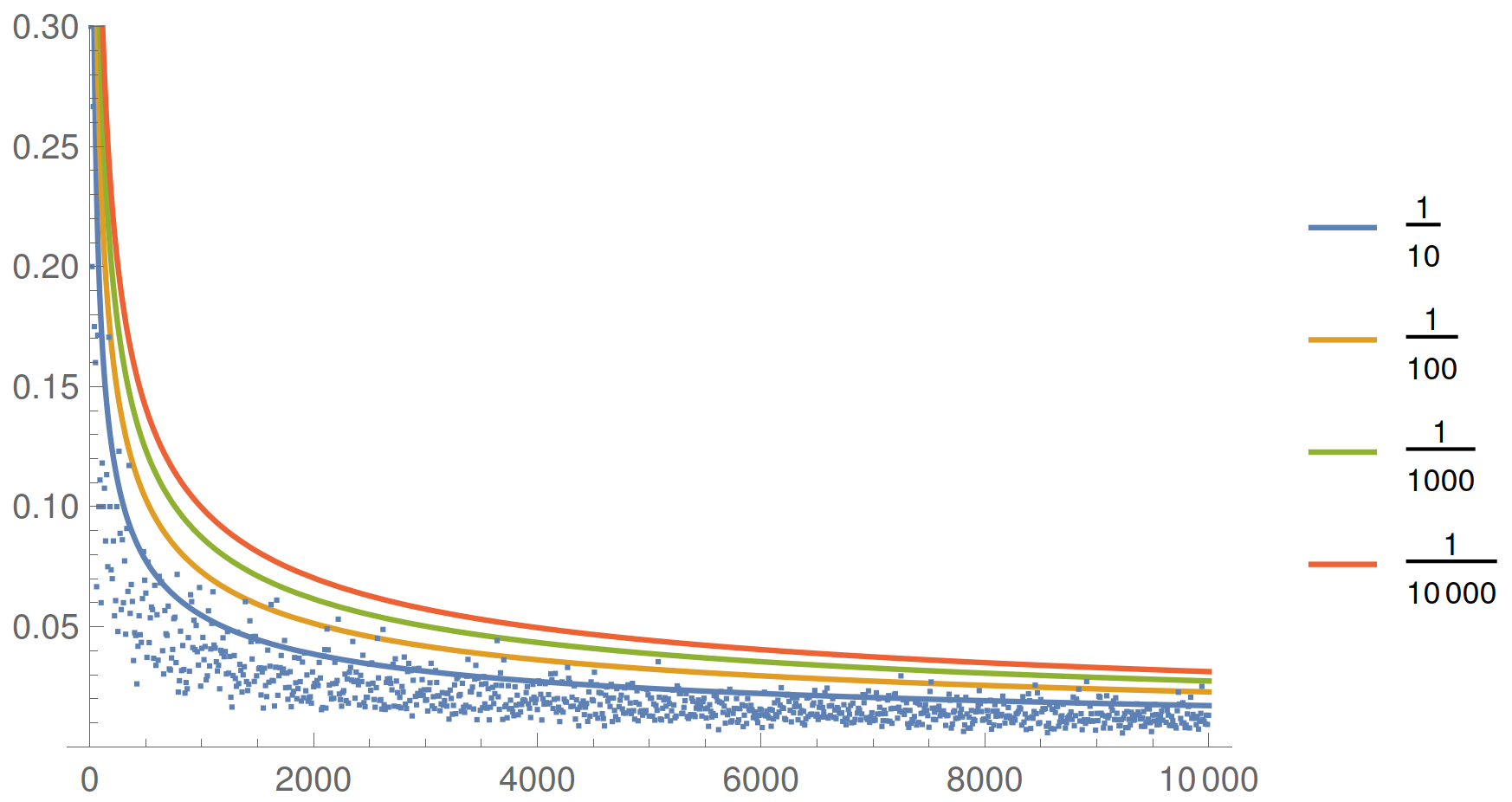
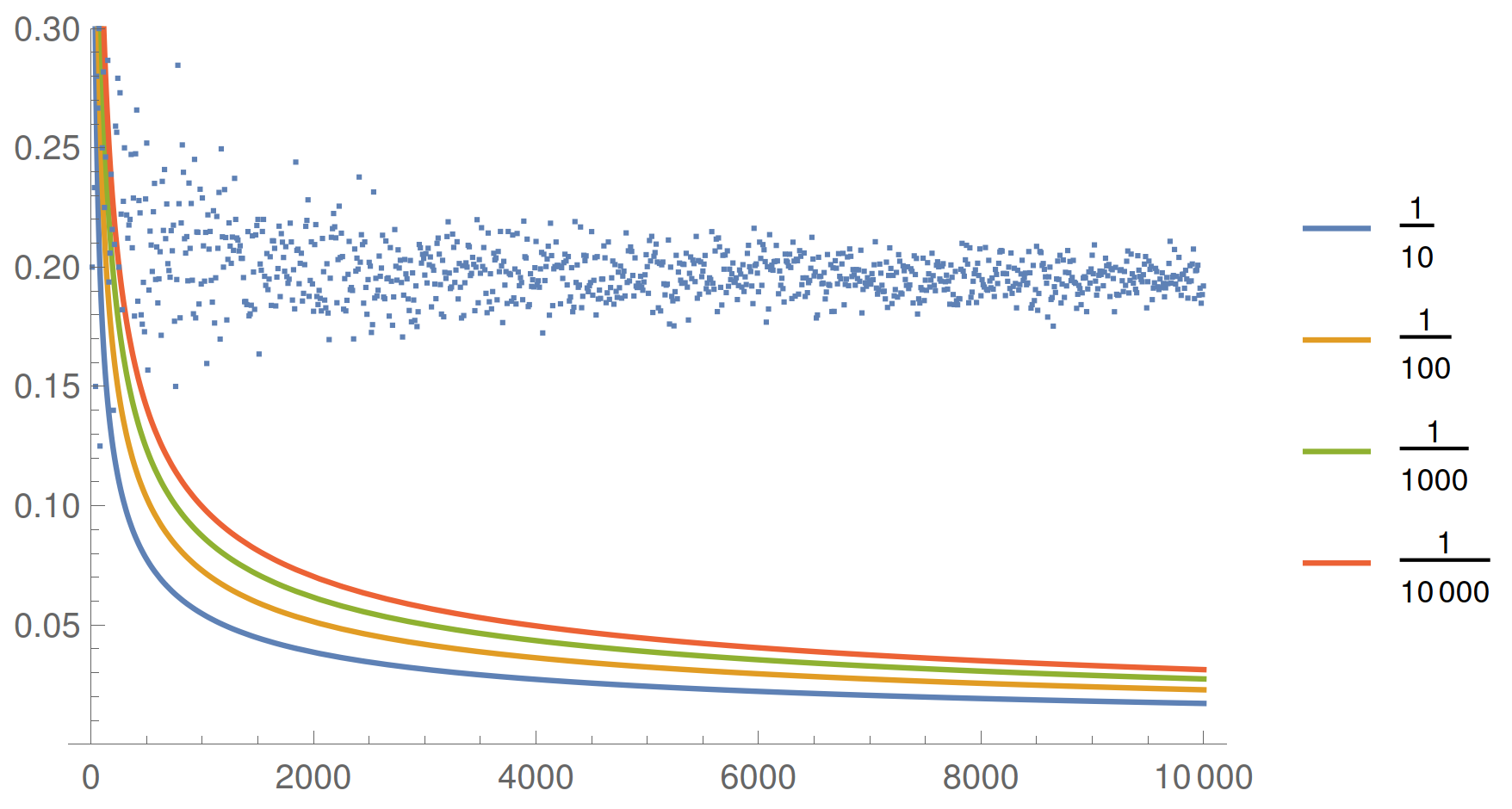
Standard tests of whether samples are drawn from the same underlying distribution are based on Smirnov's theorem, which quantifies the \(\mathcal{O}(\sqrt{\text{sample size}})\) statistical convergence of the numerically calculated distance to zero.
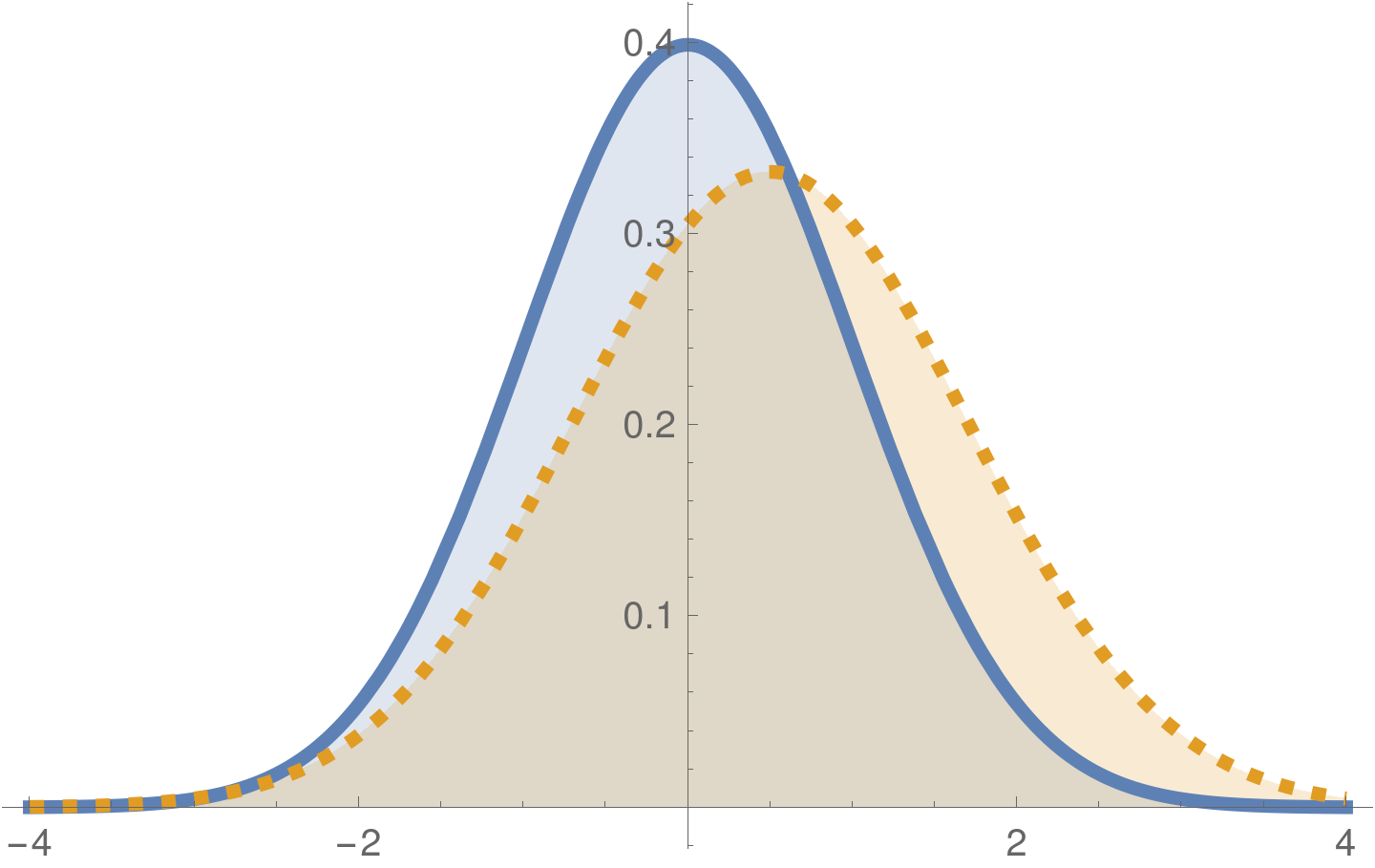
Identical PDF's
Corresponding identical CDFs
(zero KS-distance)
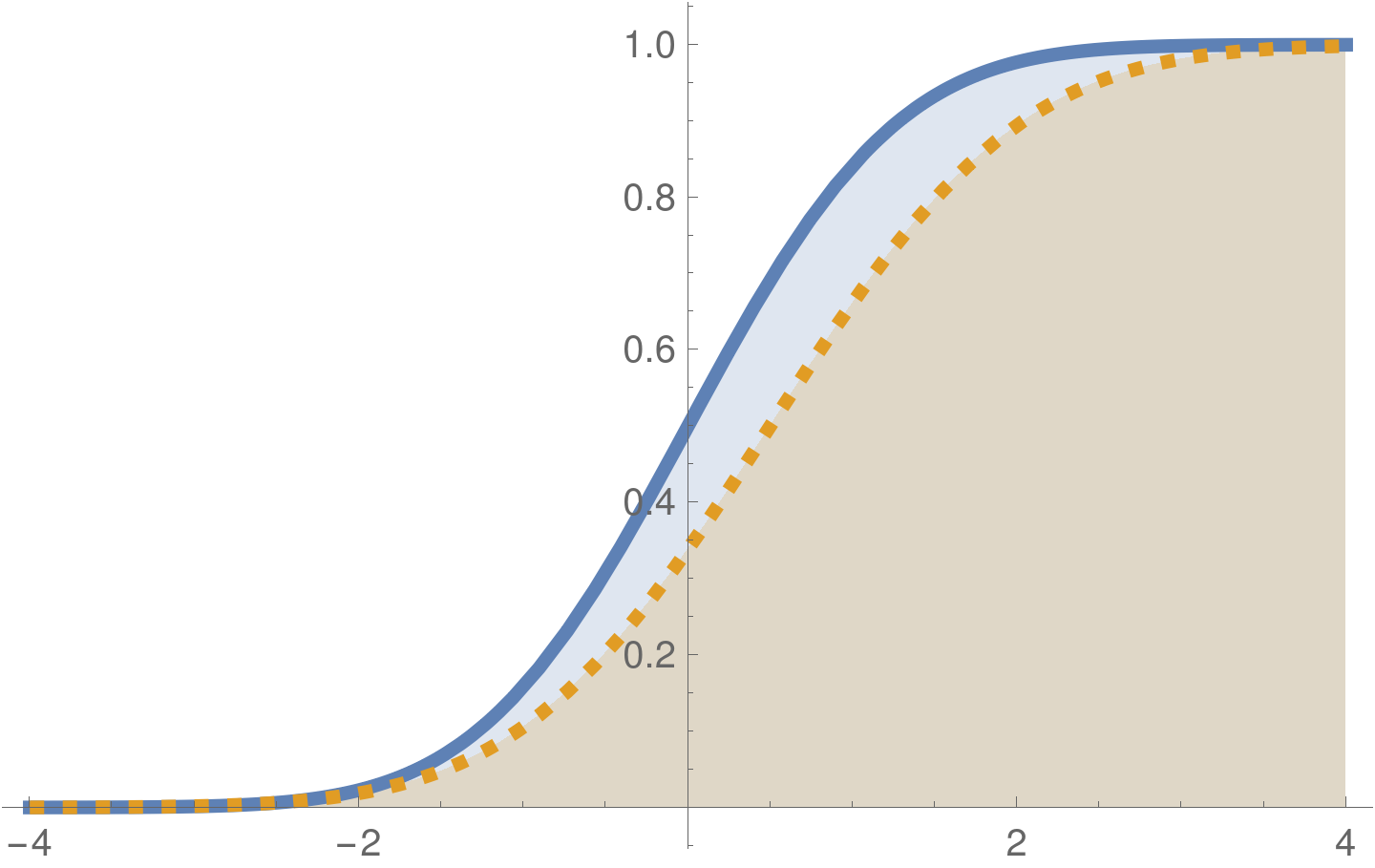
Differing PDF's
Corresponding differing CDFs (nonzero KS-distance)
True KS-distance
Zero true KS-distance
- We have been able to develop a new result that quantifies a similar \(\mathcal{O}(\sqrt{\text{sample size}})\) convergence to the true distance for differing distributions.
- This enables us to quantify the spectral resolution of the ergodicity spectrum.
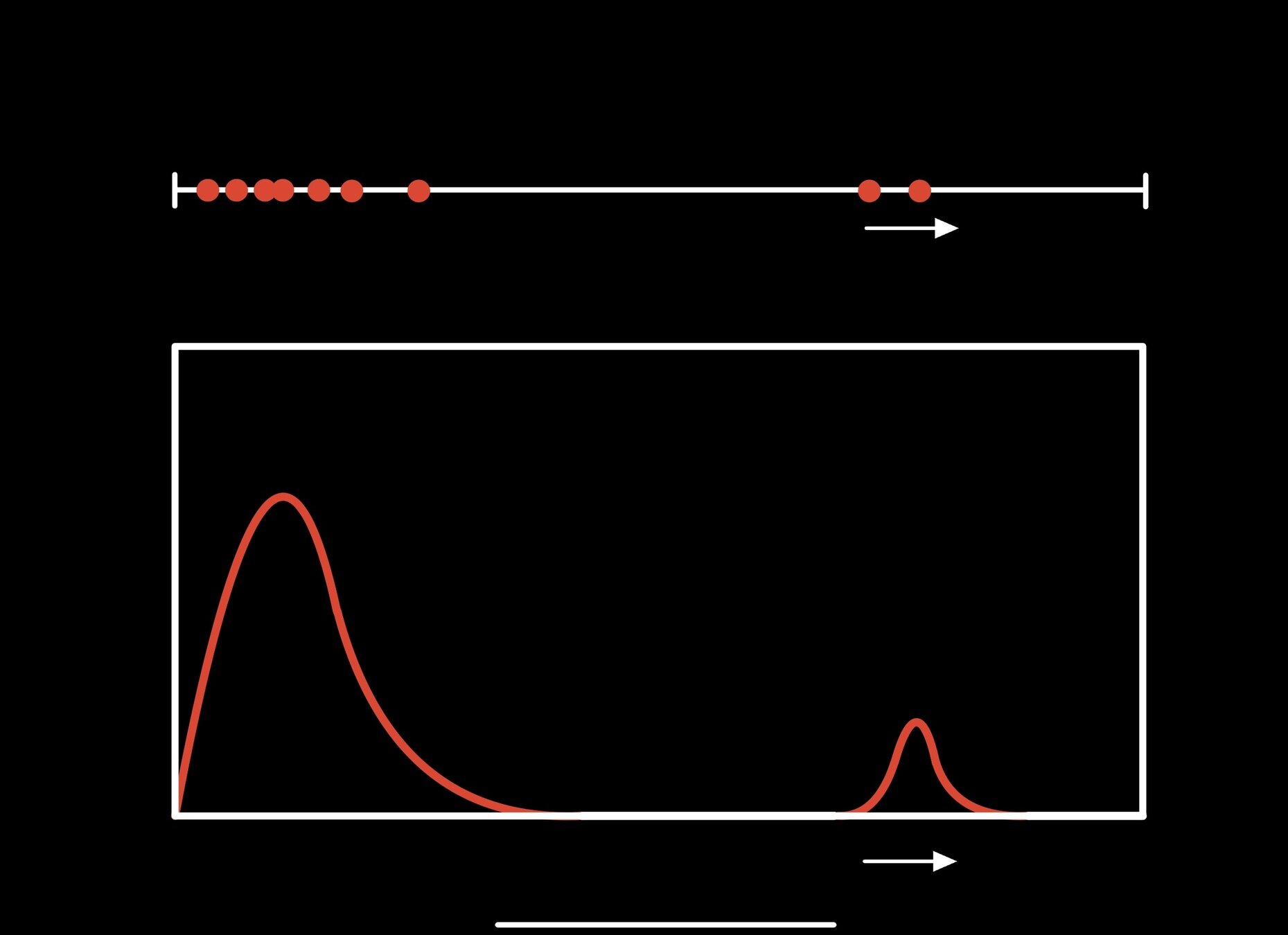
The concept of an ergodicity spectrum
Set of KS-distances calculated from an ensemble of trajectories
KS-distance (non-ergodicity)
0
1
Ergodicity spectrum constructed by histogramming KS-distances
frequency
0
1
KS-distance (non-ergodicity)
In this case:
majority of trajectories close to ergodic
In this case:
not insignificant minority displaying highly non-ergodic behaviour
The KS-value (non-ergodicity) obtained for any individual trajectory is dependent upon:
- the function being evaluated
- the initial state
- random numbers
- the total elapsed time
- Increasing sample size leads to a more accurate estimate of KS-value, and so improves spectral resolution.
- Increasing number of trajectories/KS-distances improves noise in the spectrum.
The concept of an ergodicity spectrum
Set of KS-distances calculated from an ensemble of trajectories

KS-distance (non-ergodicity)
0
1
Ergodicity spectrum constructed by histogramming KS-distances
frequency
0
1
KS-distance (non-ergodicity)
In this case:
majority of trajectories close to ergodic
In this case:
not insignificant minority displaying highly non-ergodic behaviour
Note:
Such a spectrum allows us make an analogy with the distinction between risk and harm.
We may talk about the likelihood of non-ergodicity and the degree of non-ergodicity.
Some preliminary results to illustrate...
The Kob-Andersen model at increasing density (non-trivial ergodic transition)



Actually a lattice glass model, but we could in this particular instance we could take the following crude analogy:
- A ballroom (lattice) is filled with conference participants, each eager to network.
- Each participant is in conversation with the participants immediately adjacent to them.
- At each time step each participant attempts to move around and network.
- However if they are speaking to three or more people, they get stuck in conversation and cannot move.
- And they are afraid of getting stuck in conversation so they refuse to move to a square in which they will be speaking to three or more people.
- For the phase function/observable we consider the mean contact number per participant.
Some preliminary results to illustrate...

Historgrams of the ergodic spectrum at different bin sizes
Main messages
- We have developed a new notion of spectral ergodicity that we expect could provide insight to the types of systems studied in ergodicity economics.
- It's currently undergoing benchmarking, with two papers planned for this year.
- We're looking for interesting scenarios to apply our methodology to. If you think you might be have ideas on this or wish to collaborate, please don't hesitate to contact us at:
NUnderwood@lincoln.ac.uk (Nick)
FPaillusson@lincoln.ac.uk (Fabien)
EE2023 - Ergodicity in principle and in practice - Jan 2023
By Nick Underwood
EE2023 - Ergodicity in principle and in practice - Jan 2023
EE2023 presentation
- 58



