BraInside
Algorithmes pour la Simplification
des Réseaux de Neurones
Emanuele Natale
Journée AID-INRIA
Paris, 12 Juin 2023

Centre Inria d'Université Côte d'Azur
Nécessité de comprimer les réseaux de neurones
Le Deep Learning est
devenu populaire en 2012
quand AlexNet a remporté le
concours LSVRC 2012.

AlexNet a 60
millions de
poids (environ 3 Go)
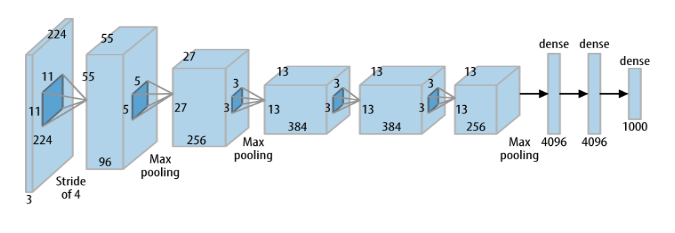

Les architectures de pointe sont “lourdes” pour certains systémes embarqués
Comment comprimer les réseaux de neurones ?
Les réseaux de neurones ont tendance à être très
“compressibles”
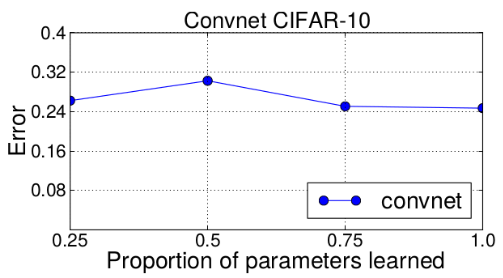
Différentes familles de techniques:
- Techniques de quantification
- Techniques
d'algèbre linéaire - Techniques
d'élagage
BraInside:
Utiliser les techniques de la théorie des algorithmes pour développer de nouvelles techniques d'élagage.
Aperçu du projet BraInside
Membres
-
Emanuele Natale (CR), INRIA UCA
-
Laurent Viennot (DR), INRIA Paris
-
Arthur Walraven da Cunha (PhD), INRIA UCA
-
Paulo Bruno Serafim (Ingénieur de recherche, 6 mois), INRIA UCA
-
Damien Rivet (Postdoc, 1 an), INRIA UCA
Production scientifique
- 4 manuscrits à publier
- OLA 2023
- ICLR 2022
- AAAI 2022
Autres produits
-
Dépôt de brevet
n° FR2210217 - Logiciel "Tinynets" en cours de développement
Élagage itéré par magnitude
Blalock et al. (2020): L'élagage itéré par magnitude est toujours une technique de compression de pointe.
entrâıner jusquà
atteindre une
bonne précision
enlever les arcs de moindre poids
ré-entrâıner le réseau pour corriger l’imprécision introduite
enlever les arcs de moindre poids
entrâıner jusquà atteindre une bonne précision
L'hypothèse du billet de loterie
Frankle & Carbin (ICLR 2019):
Un grand réseau aléatoire contient des sous-réseaux qui atteignent une précision comparable lorsqu'ils sont entraînés.
entraînement
réseau aléatoire épars
réseau épars et inefficace
entraîner et élaguer à répétition
grand réseau aléatoire
réseau épars et efficace
réseau
épars
du billet
réseau épars et efficace
réinitialisation
entraînement
L'hypothèse forte du billet de loterie
Entraînement par élagage:
Ramanujan et al. (CVPR 2020) trouvent un bon sous-réseau sans changer les poids

Un réseau avec des poids aléatoires contient des sous-réseaux qui peuvent approximer n'importe quel réseau neurones donné suffisamment plus petit
(sans entraînement)
Prouver l'hypothèse forte du billet de loterie
Malach et al. (ICML 2020)
Trouve un poids aléatoire
proche de \(w\)
Pensia et al. (NeurIPS 2020)
Trouve une combinaison de poids aléatoires proche de \(w\)
La liason avec le problème de la
somme du sous-ensemble aléatoire
Trouver une combinaison de poids aléatoires proche de \(w\):
PSSA. Pour quelle variable \(n\) l'énoncé suivant est-il valable ?
Étant donné \(X_1,...,X_n\) variables aléatoires indépendantes, avec prob. \(1-\epsilon\) pour chaque \(z\in [-1,1]\) il existe \(S\subseteq\{1,...,n\}\) tel que
\(|z-\sum_{i\in S} X_i |\leq \epsilon\).
Connexion profonde avec les programme linéaires aléatoires
[Dyer & Frieze '89,
Borst et al. '22]
Lueker '98:
\(n=O(\log \frac 1{\epsilon})\)
Réseau de neurones convolutifs
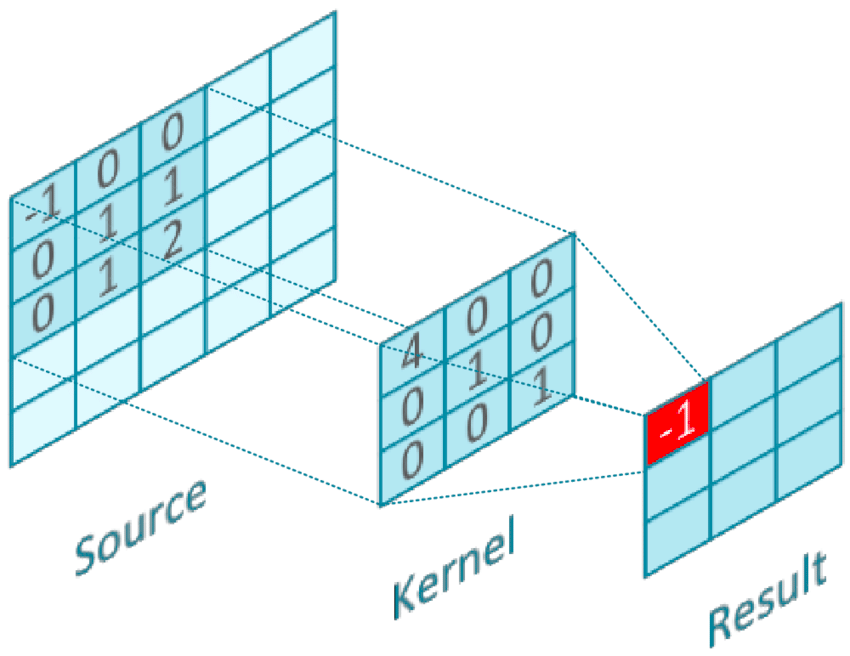
La convolution entre \(K\in\reals^{d\times d\times c}\) et \(X\in\reals^{D\times D\times c}\) est
\( \left(K * X\right)_{i,j\in\left[D\right]}=\sum_{i',j'\in\left[d\right],k\in\left[c\right]}K_{i',j',k}\cdot X_{i-i'+1,j-j'+1,k}, \)
où \(X\) est complété par des zéros. .
Un RNC simple \(N:\left[0,1\right]^{D\times D\times c_{0}}\rightarrow\mathbb{R}^{D\times D\times c_{\ell}}\) est
\[ N\left(X\right)= \sigma\left( K^{(\ell)}*\sigma\left(K^{(\ell-1)}*\sigma\left(\cdots * \sigma\left(K^{(1)} * X\right)\right)\right)\right)\]
où \(K^{(i)} \in\mathbb R^{d_{i}\times d_{i}\times c_{i-1}\times c_{i}}\).
Extension aux réseaux de neurones convolutifs
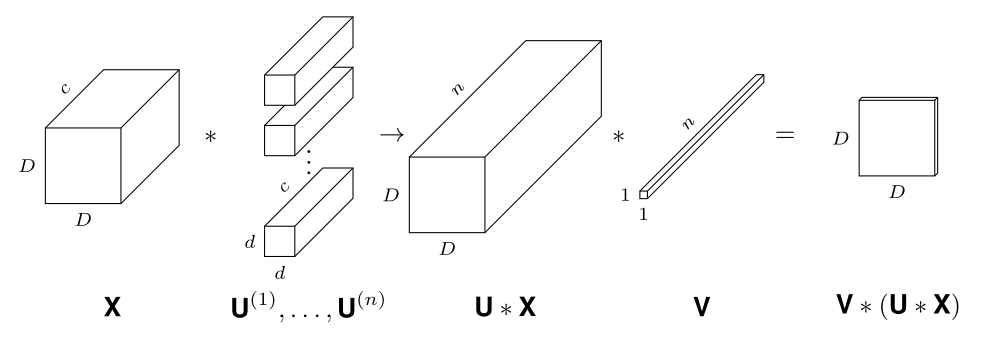
Théorème (da Cunha et al., ICLR 2022).
Étant donné \(\epsilon,\delta>0\), tout RNC avec \(k\) paramètres et \(\ell\) couches, et avec des noyaux de norme au plus constant, peut être approximé avec une erreur de \(\epsilon\) en élaguant un RNC aléatoire avec \(O\bigl(k\log \frac{k\ell}{\min\{epsilon,\delta\}}\bigr)\) paramètres et \(2\ell\) couches avec une probabilité d'au moins \(1-\delta\).
Réduire la consommation énergétique :
supports dédiés

Confier les calculs à la physique
Loi d'Ohm
Pour multiplier \(w\) et \(x\), régler \(V_{in}=x\) et \(R=\frac 1w\), puis \(I_{out}=wx\).
Dispositif à barres résistives
MVM analogique via des barres transversales de résistances programmables.

Problème : il est difficile de fabriquer des résistances programmables précises.
Cfr. ~10k FLOPS pour un MVM numérique 100x100
"Résistance équivalente modulable
à partir de résistances imprécises"
INRIA Dépôt de brevet FR2210217
Exploiter le bruit pour augmenter la précision
Théorème du SSA
Résistance programmable

Travaux à venir
Publication des 4 résultats :
- Élagage des filtres dans le RNC
- Algorithme de hachage sensible à la localité FlyHash
- Nouvelle preuve de SSA
- Nouvelle preuve du SSA multidimensionnel
Terminer le développement de la première version du logiciel d'élagage
Remerciements
INRIA : F. Segond, A. Schoofs, administration...
Collaborateurs: F. d'Amore, P. Crescenzi, I. Nachum...
DGA : R. Sol, R. Moha.
Journée AID-INRIA 2023
By Emanuele Natale
Journée AID-INRIA 2023
- 340



