On the Random
Subset Sum Problem
and Neural Networks
Emanuele Natale jointly with A. Da Cunha & L. Viennot
23 March 2023
Deep Learning on the Edge
Turing test (1950)
Today
1st AI winter (1974–1980)
2nd AI winter (1974–1980)
"A hand lifts a cup"
Use of GPUs in AI (2011)
Today, most AI heavy lifting is done in the cloud due to the concentration of large data sets and dedicated compute, especially when it comes to the training of machine learning (ML) models. But when it comes to the application of those models in real-world inferencing near the point where a decision is needed, a cloud-centric AI model struggles. [...] When time is of the essence, it makes sense to distribute the intelligence from the cloud to the edge.
Roadmap
1. ANN pruning
2. The Strong Lottery Ticket Hypothesis
3. SLTH for CNNs
4. Neuromorphic hardware
Dense ANNs
Feed-forward homogeneous dense ANN \(f\):
Application of \(\ell\) layers \(N_i\) with
\(N_i(x) = \sigma(W_i x)\),
ReLu activation \(\sigma(x)=\max(0,x)\)
and weight matrices \(W_i\), so that
\[f(x)=\sigma(W_{\ell}(\sigma(W_{\ell-1}(...(x)))).\]
Compressing ANN
Matrix techniques
Quantization techniques
Pruning techniques
Neural Network Pruning
Blalock et al. (2020): iterative magnitude pruning still SOTA pruning technique.
train
train
prune
prune
train
The Lottery Ticket Hypothesis
Frankle & Carbin (ICLR 2019):
Large random networks contains sub-networks that reach comparable accuracy when trained
train
sparse random network
sparse
bad network
..., train&prune
train&prune, ...,
large random network
sparse good network
train
sparse "ticket" network
sparse
good network
rewind
Roadmap
1. ANN pruning
2. The Strong Lottery Ticket Hypothesis
3. SLTH for CNNs
4. Neuromorphic hardware
The Strong LTH
Ramanujan et al. (CVPR 2020) find a good subnetwork without changing weights (train by pruning!)
A network with random weights contains sub-networks that can approximate any given sufficiently-smaller neural network (without training)
Formalizing the SLTH
Random network \(R_0\) with \(h\cdot d\) parameters
lottery ticket
\(N_{L}\subseteq N_0\)
Target network that solves task \(N_T\)
with \(d\) parameters
\approx
Proving the SLTH
Malach et al. (ICML 2020)
w
w_1
w_n
Find random weight
close to \(w\)
Idea: Find patterns in the random networks which are equivalent to sampling a weight until you are lucky.
Q: How many uniform\((-1,1)\) sample to approximate \(z\) up to \(\epsilon\)?
Malach et al.'s Idea
Suppose \(x\) and all \(w'_i\)s are positive, then
\[y=\sum_i w_i\sigma(w'_i x) = \sum_i w_i w'_i x \]
For general \(x\), use the ReLu trick \(x=\sigma(x)-\sigma(-x)\):
\[y= \sum_{i:w'_i\geq 0} w_i\sigma(w'_i x)+\sum_{i:w'_i<0} w_i\sigma(w'_i x) \]
\[= \sum_{i:w'_i\geq 0} w_i w'_i x {\mathbb 1}_{x\geq 0}+\sum_{i:w'_i<0} w_i w'_i x {\mathbb 1}_{x< 0}\]
w_1
w_n
w'_n
w'_1
x
y
Better Bound for SLTH
(assume \(x\) and \(w'_i\)s are positive)
\(y= \sum_{i} w_i w'_i x \)
Pensia et al. (NeurIPS 2020)
w
Find combination of random weights close to \(w\)
alternative in Orseau et al. (Neurips 2020)
w_1
w_n
w'_n
w'_1
x
y
RSSP. Given \(X_1,...,X_n\) i.i.d. random variables, with prob. \(1-\epsilon\) for each \(z\in [-1,1]\) find a subset \(S\subseteq\{1,...,n\}\) such that \(|z-\sum_{i\in S} X_i |\leq \epsilon.\)
Lueker '98. Solution exists with prob. \(1-\epsilon\) if \(n=O(\log \frac 1{\epsilon})\).
RSS - Proof Idea 1/2
If \(n=O(\log \frac 1{\epsilon})\), given \(X_1,...,X_n\) i.i.d. random variables, with prob. \(1-\epsilon\) for each \(z\in [-\frac 12, \frac 12]\) there is \(S\subseteq\{1,...,n\}\) such that \(|z-\sum_{i\in S} X_i |\leq \epsilon.\)
Let \(f_t(z)=\mathbf 1(z\in (-\frac 12, \frac 12),\exists S\subseteq\{1,...,t\}: |z-\sum_{i\in S} X_i |\leq \epsilon)\)
then \(f_t(z)=f_{t-1}(z)+(1-f_{t-1}(z))f_{t-1}(z-X_t)\).
Observation: If we can approximate any \(z\in (a,b)\) and we add \(X'\) to the sample, then we can approximate any
\(z\in (a,b) \cup (a+X',b+X')\).
RSS - Proof Idea 2/2
\(z\in(-\frac 12, \frac 12), f_t(z)=f_{t-1}(z)+(1-f_{t-1}(z))f_{t-1}(z-X_t)\).
\(\int_{-\frac 12}^{\frac 12}f_{t-1}(z)dz+\mathbb E[\int_{-\frac 12}^{\frac 12}(1-f_{t-1}(z))f_{t-1}(z-X_t)dz|\,X_{t-1},...,X_1]\)
\(=v_{t-1}+\frac 12 (1-v_{t-1})v_{t-1}.\)
\(=v_{t-1}+\frac 12 \int_{-1}^{1}[\int_{-\frac 12}^{\frac 12}(1-f_{t-1}(z))f_{t-1}(z-x)dz]dx\)
\(=v_{t-1}+\frac 12 \int_{-\frac 12}^{\frac 12}(1-f_{t-1}(z))[\int_{-1}^{1}f_{t-1}(z-x)dx]dz\)
\(=v_{t-1}+\frac 12 \int_{-\frac 12}^{\frac 12}(1-f_{t-1}(z))[\int_{z-1}^{z+1}f_{t-1}(s)ds]dz\)
\(=v_{t-1}+\frac 12 \int_{-\frac 12}^{\frac 12}(1-f_{t-1}(z))[\int_{-\frac 12}^{\frac 12}f_{t-1}(s)ds]dz\)
\(\mathbb E[v_t\,|\,X_{t-1},...,X_1]=\)
Let \(v_t=\int_{-\frac 12}^{\frac 12}f_t(z)dz\), then
"Revisiting the Random Subset Sum problem" https://hal.science/hal-03654720/
s = z-x
Roadmap
1. ANN pruning
2. The Strong Lottery Ticket Hypothesis
3. SLTH for CNNs
4. Neuromorphic hardware
Convolutional Neural Network
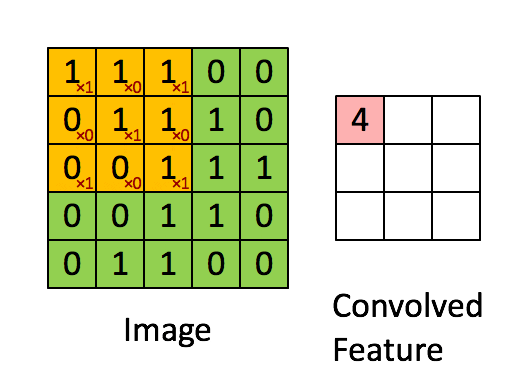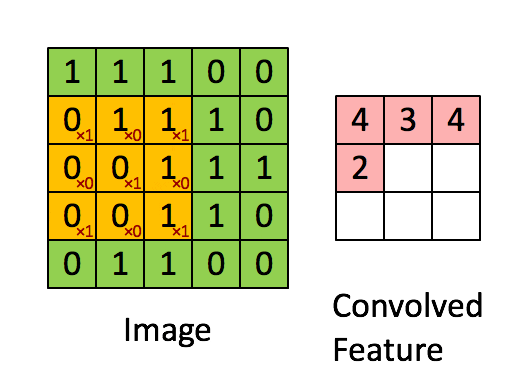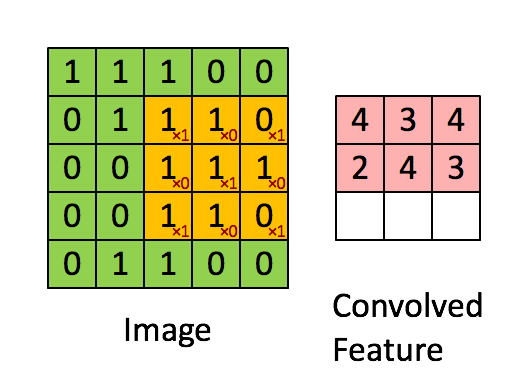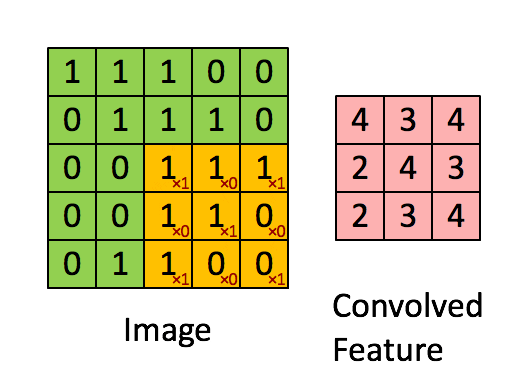
The convolution of \(K\in\reals^{d\times d\times c}\) and \(X\in\reals^{D\times D\times c}\) is \( \left(K * X\right)_{i,j\in\left[D\right]}=\)\[\sum_{i',j'\in\left[d\right],k\in\left[c\right]}K_{i',j',k}\cdot X_{i-i'+1,j-j'+1,k}, \]
where \(X\) is zero-padded.
A simple CNN \(N:\left[0,1\right]^{D\times D\times c_{0}}\rightarrow\mathbb{R}^{D\times D\times c_{\ell}}\) is defined as
\[ N\left(X\right)= \sigma\left( K^{(\ell)}*\sigma\left(K^{(\ell-1)}*\sigma\left(\cdots * \sigma\left(K^{(1)} * X\right)\right)\right)\right)\]
where \(K^{(i)} \in\mathbb R^{d_{i}\times d_{i}\times c_{i-1}\times c_{i}}\).
2D Discrete Convolution
If \(K\in\reals^{d\times d\times c_{0}\times c_{1}}\) and \(X\in\reals^{D\times D\times c_{0}}\)
\[ \left(K * X\right)_{i,j\in\left[D\right],\ell\in\left[c_{1}\right]}=\sum_{i',j'\in\left[d\right],k\in\left[c_{0}\right]}K_{i',j',k,\ell}\cdot X_{i-i'+1,j-j'+1,k}.\]
SLTH for Convolutional Neural Networks
Theorem (da Cunha et al., ICLR 2022).
Given \(\epsilon,\delta>0\), any CNN with \(k\) parameters and \(\ell\) layers, and kernels with \(\ell_1\) norm at most 1, can be approximated within error \(\epsilon\) by pruning a random CNN with \(O\bigl(k\log \frac{k\ell}{\min\{\epsilon,\delta\}}\bigr)\) parameters and \(2\ell\) layers with probability at least \(1-\delta\).
Proof Idea 1/2
For any \(K\in [-1,1]^{d\times d\times c\times1}\) with \(\|K\|_{1}\leq1\) and \(X\in [0,1]^{D\times D\times c}\) we want to approximate \(K*X\) with \(V*\sigma(U*X)\) where \(U\) and \(V\) are tensors with i.i.d. \(\text{Uniform}(-1,1)\) entries.
Let \(U\) be \(d\times d \times c\times n\) and \(V\) be \(1\times 1 \times n \times 1\).
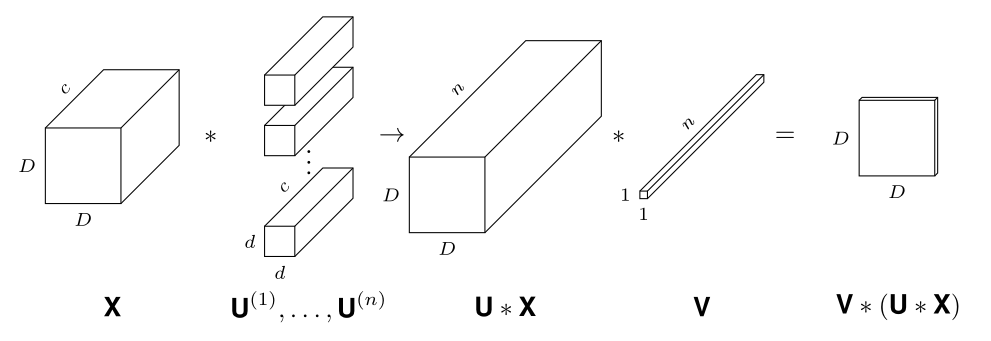
Proof Idea 2/2
\left(V*\left(U* X\right)\right)_{r,s,1}
=\sum_{t=1}^{n}V_{1,1,t,1}\cdot\left(U* X\right)_{r,s,t}\\
=\sum_{t=1}^{n}V_{1,1,t,1}\cdot\left(\sum_{i,j\in\left[d\right],k\in\left[c\right]}U_{i,j,k,t}\cdot X_{r-i+1,s-j+1,k}\right)_{r,s,t}\\
=\sum_{t=1}^{n}\sum_{i,j\in\left[d\right],k\in\left[c\right]}\left(V_{1,1,t,1}\cdot U_{i,j,k,t}\right)\cdot X_{r-i+1,s-j+1,k}\\
=\sum_{i,j\in\left[d\right],k\in\left[c\right]}\left(\sum_{t=1}^{n}V_{1,1,t,1}\cdot U_{i,j,k,t}\right)\cdot X_{r-i+1,s-j+1,k}\\
=\sum_{i,j\in\left[d\right],k\in\left[c\right]}L_{i,j,k,1}\cdot X_{r-i+1,s-j+1,k}
where \(L_{i,j,k,1}=\sum_{t=1}^{n}V_{1,1,t,1}\cdot U_{i,j,k,t}\)
Prune negative entries of \(U\) so that \(\sigma(U*X)=U*X\).
Roadmap
1. ANN pruning
2. The Strong Lottery Ticket Hypothesis
3. SLTH for CNNs
4. Neuromorphic hardware
Reducing Energy: the Hardware Way
Letting Physics Do The Math
Ohm's law
V_{in}
R
R
I_{out}\\=\frac{V_{in}}{R}
To multiply \(w\) and \(x\), set \(V_{in}=x\) and \(R=\frac 1w\), then \(I_{out}=wx\).
Resistive Crossbar Device
Analog MVM via crossbars of programmable resistances
Problem: Making precise programmable resistances is hard
Cfr. ~10k flops for digital 100x100 MVM
"Résistance équivalente modulable
à partir de résistances imprécises"
INRIA Patent deposit FR2210217
Leverage noise itself
to increase precision
RSS
Theorem
Programmable
effective resistance
RSS in Practice
bits of precision for any target value are linear w.r.t. number of resistances
Worst case among
2.5k instances
Conclusions
RSS theory provides a fundamental tool for understanding the relation between noise and sparsification.
Open problem. SLTH for neural pruning, i.e. removing entire neurons in dense ANNs.
Thank you
GSSI 2023
By Emanuele Natale
