N-Queens 問題
Nobuhide Tsuda
26-May-2013
※ HTML版もあるよ
自己紹介
名前:津田伸秀
facebook:https://www.facebook.com/nobuhide.tsuda
twitter:vivisuke
枕詞:年齢不詳のおじさん
趣味:テニス、オセロ、思考ゲーム・パズル類
Qt/VC++ 使いの C++er, 一応webアプリも出来るよ
Windows用テキストエディタ ViVi を延々開発してます
Android・tmlib のパズルアプリも公開中だよ
迷走中
Contents
-
はじめに
- 力まかせ探索(Brute-force search)
- バックトラッキング
- 制約テスト高速化(配置フラグ)
- ビット演算(ビットマップ)による高速化
- 対称解除去
- 枝刈りによる高速化
- さいごに
- 参考文献
はじめに
-
N-Queens 問題とは、NxNの盤面にチェスのクイーンN個を互いに効きが無いように配置する問題
-
クイーンは縦横斜めの8方向の効きを持つ
-
8-Queens は 8x8 のチェス盤を用いる問題で、N-Queens 問題はそれを一般化したもの
-
参照:
エイト・クイーン
-
解の総数は92個。対称形を除いたユニーク解は12個
-
次図に12個のユニーク解の一覧を示す
8-Queens 程度であれば、力まかせ探索でも解を求めることができるが、N が大きくなると場合の数が爆発し、実用的な時間では解けなくなる
- 制約充足問題 に分類される
- 解の候補が与えられた時に、それが制約を満たすかどうかが簡単・高速に判定可能な問題
-
本稿では数種のアルゴリズム・データ構造により N-Queens 問題を解くプログラムを実装し、パフォーマンス計測を行う
- 最初は対称解の排除は行わず、すべての解を求める
- いで、対称解を排除し、ユニーク解のみを求める
- ソースコード記述言語は C++ を用いた。
- 高速化のため、ボードサイズを引数で渡すのではく、テンプレート引数で指定するようにした
- パフォーマンス計測環境:Core i5 670@3.47GHz 12GBMem Win7x64 VC10.0(32bit) Qt 4.8 QTest
力まかせ探索(Brute-force search)
-
全ての可能性のある解の候補を体系的に数えあげ、それぞれの解候補が問題の解となるかをチェックする方法
- パターン生成後にチェックするので「生成検査法(generate & test)」とも呼ばれる
-
8-Queens の場合:
-
64箇所に8個のクイーンを置く場合の数は、
64 C 8 = 4.4*10^9 -
各行には1個のクイーンしか置けないので、
8^8 = 16,777,216 で充分 -
N-Queens 問題の処理時間は O(N^N) となる
-
int row[NQ]; に各行のクイーン位置([1, NQ])を保持
-
関数 test() で効きのチェックを行う
- 処理速度はかなり遅く、実用的ではない
N重ループによるコード
int row[NQ]; // 各行のクイーン位置 [1, NQ]for(row[0] = 1; row[0] <= NQ; ++row[0]) { .... for(row[NQ-1] = 1; row[NQ-1] <= NQ; ++row[NQ-1]) { if( 制約を満たしているか? ) { 解を発見; } } .... }
再帰関数によるコード(ボードサイズはテンプレート引数で付与)
bool test(const int row[], int n) // n:配置済みクイーン数
{
for(int r = 1; r < n; ++r) {
for(int i = 0; i < r; ++i) {
if( row[i] == row[r] || qAbs(row[i] - row[r]) == r - i )
return false;
}
}
return true;
}
template<int NQ>
void generateAndTest(int row[], int n) // 配置済みクイーン数
{
for(row[n] = 1; row[n] <= NQ; ++row[n]) {
if( n + 1 == NQ ) {
if( test<NQ>(row) )
++g_count; // 解を発見
} else
generateAndTest<NQ>(row, n+1);
}
}
パフォーマンス測定結果:
| N | 解の数 | 末端ノード数 | Brute-Force (ミリ秒) |
|---|---|---|---|
| 4 | 2 | 256 | 0 |
| 5 | 10 | 3,125 | 1 |
| 6 | 4 | 46,656 | 1 |
| 7 | 40 | 823,543 | 10 |
| 8 | 92 | 16,777,216 | 150 |
| 9 | 352 | 387,420,489 | 3,317 |
- 探索速度:約1*10^8 NPS
- 最近のCPUはウン10年前に比べると、恐ろしく高速なので 8-Queens 程度であれば力ずくでもなんとかなる
バックトラッキング
- パターンを生成し終わってからチェックを行うのではなく、途中で制約を満たさないことが明らかな場合は、 それ以降のパターン生成を行わない
- N-Queens 問題の処理時間は O(N!) 程度?となる
bool testNth(const int row[], int n) { for(int i = 0; i < n; ++i) { if( row[i] == row[n] || qAbs(row[i] - row[n]) == n - i ) return false; } return true; }template<int NQ> void backtracking(int row[], int n) // n:配置済みクイーン数 { for(row[n] = 1; row[n] <= NQ; ++row[n]) { if( testNth(row, n) ) { // 制約を満たしている場合のみ先に進む if( n + 1 == NQ ) ++g_count; // 解を発見 else backtracking<NQ>(row, n+1); } } }
パフォーマンス測定結果:
| N | 解の数 | 末端ノード数 | Backtracking (ミリ秒) | BF (ミリ秒) |
|---|---|---|---|---|
| 4 | 2 | 46 | 0 | 0 |
| 5 | 10 | 177 | 0 | 1 |
| 6 | 4 | 746 | 0 | 1 |
| 7 | 40 | 3,073 | 0 | 10 |
| 8 | 92 | 13,756 | 1 | 150 |
| 9 | 352 | 64,337 | 2 | 3,317 |
| 10 | 724 | 313,336 | 9 | N/A |
| 11 | 2,680 | 1,642,461 | 49 | N/A |
| 12 | 14,200 | 9,261,880 | 220 | N/A |
| 13 | 73,712 | 55,214,137 | 1,434 | N/A |
| 14 | 365,596 | 350,908,442 | 9,271 | N/A |
- 処理量が O(N^N) → O(N!) となり、無駄な解候補生成が無くなった分、高速になった
- 探索速度:約3.8*10^7 NPS
制約テスト高速化(配置フラグ)
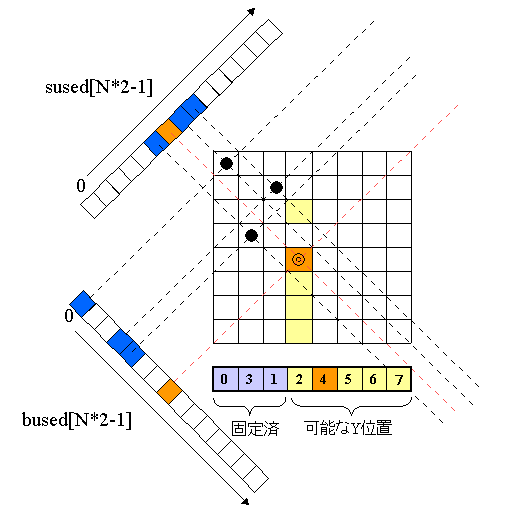
- 各列、対角線上にクイーンがあるかどうかのフラグを用意することで高速化を図る
- 詳細は8クイーン|Nクイーン by パソコン初心者氏 を参照
- 下図は上記サイトから引用。各フラグを図示
template<int NQ>
void backtrackingFlags(
bool col[], bool rup[], bool rdn[], // 垂直・対角線方向に配置済みフラグ
int n) // n:配置済みクイーン数, [0, NQ)
{
for(int q = 0; q < NQ; ++q) {
const int uix = n + q;
const int dix = q - n + NQ - 1;
if( !col[q] && !rup[uix] && !rdn[dix] ) {
if( n + 1 == NQ )
++g_count; // 解を発見
else {
col[q] = true;
rup[uix] = true;
rdn[dix] = true;
backtrackingFlags<NQ>(col, rup, rdn, n+1);
col[q] = false;
rup[uix] = false;
rdn[dix] = false;
}
}
}
}
template<int NQ>
void backtrackingFlags(
bool col[], bool rup[], bool rdn[], // 垂直・対角線方向に配置済みフラグ
int n) // n:配置済みクイーン数, [0, NQ)
{
for(int q = 0; q < NQ; ++q) {
const int uix = n + q;
const int dix = q - n + NQ - 1;
if( !col[q] && !rup[uix] && !rdn[dix] ) {
if( n + 1 == NQ )
++g_count; // 解を発見
else {
col[q] = true;
rup[uix] = true;
rdn[dix] = true;
backtrackingFlags<NQ>(col, rup, rdn, n+1);
col[q] = false;
rup[uix] = false;
rdn[dix] = false;
}
}
}
}
パフォーマンス測定結果:
| N | 解の数 | 末端ノード数 | Flag (ミリ秒) | BT (ミリ秒) | BF (ミリ秒) |
|---|---|---|---|---|---|
| 4 | 2 | 46 | 0 | 0 | 0 |
| 5 | 10 | 177 | 0 | 0 | 1 |
| 6 | 4 | 746 | 0 | 0 | 1 |
| 7 | 40 | 3,073 | 0 | 0 | 10 |
| 8 | 92 | 13,756 | 0 | 1 | 150 |
| 9 | 352 | 64,337 | 1 | 2 | 3,317 |
| 10 | 724 | 313,336 | 3 | 9 | N/A |
| 11 | 2,680 | 1,642,461 | 14 | 49 | N/A |
| 12 | 14,200 | 9,261,880 | 53 | 220 | N/A |
| 13 | 73,712 | 55,214,137 | 316 | 1,434 | N/A |
| 14 | 365,596 | 350,908,442 | 1,813 | 9,271 | N/A |
- 前章の方法では、重複チェックに O(N) の時間を要するが、フラグを利用することで O(1) に短縮される
- 単純なバックトラッキング法に比べ、4倍程度高速になった
- 探索速度:約1.9*10^8 NPS、末端ノード数に変化は無いが、NPSが向上
ビット演算(ビットマップ)による高速化
- ビット演算によりさらに高速化を図る
- 状態をビットマップにパックし、処理する
- 各カラムに配置可能かどうかを cols で表す(初期値は (1<<NQ)-1)
- N = 32 or 64 が上限となり、配列に比べるとスケーラビリティに劣る
- が、世界記録(2009年7月)でも N = 26 なので、32 が上限でも問題にならない
表 1 N クイーン問題の最新状況
| N | 公表日 | すべての解の数 | unique解の数 |
| 24 | 2004.04.11 | 227,514,171,973,736 | 28,439,272,956,934 |
| 25 | 2005.06.11 | 2,207,893,435,808,350 | 275,986,683,743,434 |
| 26 | 2009.07.11 | 22,317,699,616,364,000 | 2,789,712,466,510,280 |
| 27 | 未解決 |
- 斜め方向にクイーンを配置したかどうかをビットマップのフラグで表す(lt, rt)
- ビットマップであれば、シフトにより高速にデータを移動できる
- フラグ配列ではデータの移動に O(N) の時間がかかるが、ビットマップであれば O(1)
- 前章のフラグ配列のように斜め方向に 2*N-1 の要素を用意するのではなく N ビットで充分
- 初期値は0
- これはビット演算(ビットマップ)でよく使用するテクニックのひとつである
- -x = ~x + 1 であることを考えると、分かりやすい
template<int NQ>
void backtrackingBitmap(uint cols, // 配置可能カラム位置
uint lt, uint rt, // 1 for 使用済み
int n) // n:配置済みクイーン数, [0, NQ)
{
uint flags = ~(lt|rt) & cols;
while( flags ) {
uint bit = -flags & flags; // 一番右の1のビットを取り出す
if( n + 1 == NQ )
++g_count; // 解を発見
else
backtrackingBitmap<NQ>(cols^bit, (lt|bit)<<1, (rt|bit)>>1, n+1);
flags ^= bit; // 処理済みビットをOFF
}
}| N | 解の数 | 末端ノード数 | Bitmap (ミリ秒) | Flag (ミリ秒) | BT (ミリ秒) | BF (ミリ秒) |
|---|---|---|---|---|---|---|
| 4 | 2 | 6 | 0 | 0 | 0 | 0 |
| 5 | 10 | 14 | 0 | 0 | 0 | 1 |
| 6 | 4 | 50 | 0 | 0 | 0 | 1 |
| 7 | 40 | 194 | 0 | 0 | 0 | 10 |
| 8 | 92 | 736 | 0 | 0 | 1 | 150 |
| 9 | 352 | 2,936 | 0 | 1 | 2 | 3,317 |
| 10 | 724 | 12,774 | 0 | 3 | 9 | N/A |
| 11 | 2,680 | 61,076 | 2 | 14 | 49 | N/A |
| 12 | 14,200 | 314,730 | 10 | 53 | 220 | N/A |
| 13 | 73,712 | 1,716,652 | 50 | 316 | 1,434 | N/A |
| 14 | 365,596 | 10,030,692 | 298 | 1,813 | 9,271 | N/A |
| 15 | 2,279,184 | 62,518,772 | 1,805 | N/A | N/A | N/A |
| 16 | 14,772,512 | 415,515,376 | 12,179 | N/A | N/A | N/A |
- 計算量(オーダー)は変わっていないが、単純なバックトラッキング法よりも20~30倍程度高速になった。
- 探索速度:約3.4*10^7 NPS、NPSが減少するも、末端ノード数がそれ以上に減少
- 配置可能な場所を dn, lt, rt のビット演算で求め、可能な場所についてのみ処理しているので、 配置不可能な位置は末端ノードとしてはカウントしていない
- パターンを生成してから重複チェックを行うのではなく、解の可能性があるかどうかを予めチェックし、 無ければバックトラッキングを行うという方法(Forward Checking 法)もある
- が、実装して速度計測してみたところ Bitmap 法よりも遅くなってしまった
- Bitmap 法があまりに単純・高速なためにパターンの生成と単なるチェックに処理時間差が無いためと考えられる
対称解除去
- ひとつの解には、盤面を90度・180度・270度回転、及びそれらの鏡像の合計8個の対称解が存在する
12 41 34 23 43 32 21 14 21 14 43 32 34 23 12 41
- 上図左上がユニーク解。1行目はユニーク解を90度、180度、270度回転したもの
- 2行目は1行目のそれぞれを左右反転したもの。
- 2行目はユニーク解を左右反転、対角反転、上下反転、逆対角反転したものとも解釈可
- ただし、回転・線対称な解もある
- 対称的な解を除去し、ユニーク解のみを求める方法はいくつかあるが、解がみつかるとすべての対称解を生成し、 状態を数値とみなして最も小さいもののみを解とする方法(最小解選択法)が優れる
- 状態→数値の変換方法は任意である
- 変換された数値を「ユニーク判定値」と呼ぶ
- 例えば、各行のクイーン位置を数値(1~N)で表したN桁の数で充分
- 上図の様な場合、数値を4桁の数とみなすと、左上の「1243」が最小であり、ユニーク解となる
- 解を全て保存しておき、新しい解が発見されるたびに対称形が無いかどうかを調べる方法もあるが、 保存領域を必要とするし、比較時に対称形を生成する必要があり、最小解選択法より劣る
uint g_row[MAX_N]; // ボード状態// 90度、180度、270度回転・およびその鏡像よりも小さいか等しい場合は true を返す
template<int NQ>
bool checkSymmetryBitmap()
{
uint t[NQ], t2[NQ];
revHorzBitmap<NQ>(g_row, t2);
if( less<NQ, uint>(t2, g_row) ) return false;
rotateBitmap90<NQ>(g_row, t);
if( less<NQ, uint>(t, g_row) ) return false;
revHorzBitmap<NQ>(t, t2);
if( less<NQ, uint>(t2, g_row) ) return false;
rotateBitmap90<NQ>(t, t2);
if( less<NQ, uint>(t2, g_row) ) return false;
revHorzBitmap<NQ>(t2, t);
if( less<NQ, uint>(t, g_row) ) return false;
rotateBitmap90<NQ>(t2, t);
if( less<NQ, uint>(t, g_row) ) return false;
revHorzBitmap<NQ>(t, t2);
if( less<NQ, uint>(t2, g_row) ) return false;
return true;
}
template<int NQ>
void backtrackingBitmapS(uint cols,
uint lt, uint rt, // 1 for 使用済み
int n) // n:配置済みクイーン数, [0, NQ)
{
uint flags = ~(lt|rt) & cols;
if( n + 1 == NQ ) {
if( flags != 0 ) {
g_row[n] = flags;
if( checkSymmetryBitmap<NQ>() ) {
++g_count;
}
}
} else {
while( flags ) {
uint bit = -flags & flags; // 一番右の1のビットのみ取り出す
g_row[n] = bit;
backtrackingBitmapS<NQ>(cols^bit, (lt|bit)<<1, (rt|bit)>>1, n+1);
flags ^= bit; // 処理済みビットをOFF
}
}
}パフォーマンス測定結果:
| N | ユニーク解数 | 対称形除去(ミリ秒) | 解数 | Bitmap (ミリ秒) | Flag (ミリ秒) | BT (ミリ秒) |
|---|---|---|---|---|---|---|
| 4 | 1 | 0 | 2 | 0 | 0 | 0 |
| 5 | 2 | 0 | 10 | 0 | 0 | 0 |
| 6 | 1 | 0 | 4 | 0 | 0 | 0 |
| 7 | 6 | 0 | 40 | 0 | 0 | 0 |
| 8 | 12 | 0 | 92 | 0 | 0 | 1 |
| 9 | 46 | 1 | 352 | 0 | 1 | 2 |
| 10 | 92 | 0 | 724 | 0 | 3 | 9 |
| 11 | 341 | 3 | 2,680 | 2 | 14 | 49 |
| 12 | 1,787 | 14 | 14,200 | 10 | 53 | 220 |
| 13 | 9,233 | 79 | 73,712 | 50 | 316 | 1,434 |
| 14 | 45,752 | 449 | 365,596 | 298 | 1,813 | 9,271 |
| 15 | 285,053 | 3,001 | 2,279,184 | 1,805 | N/A | N/A |
| 16 | 1,846,955 | 20,142 | 14,772,512 | 12,179 | N/A | N/A |
-
ビットマップ法に比べ、探索局面数は変わらないのに対称解除去の処理が増えた分、処理時間を要している
枝刈りによる高速化
- 前章のコードは全ての解を求めた後に、ユニーク解以外の対称解を除去していた
- ある意味、「生成検査法(generate & test)」と同じである
- 問題の性質を分析し、バックトラッキング/前方検査法と同じように、無駄な探索を省略することを考える
- ユニーク解に対する左右対称解を予め削除するには、1行目のループのところで、 右半分だけにクイーンを配置するようにすればよい
- Nが奇数の場合、クイーンを1行目中央に配置する解は無い。
- 他の3辺のクィーンが中央に無い場合、その辺が上辺に来るよう回転し、場合により左右反転することで、 最小値解とすることが可能だから、中央に配置したものしかユニーク解には成り得ない
- しかし、上辺とその他の辺の中央にクィーンは互いの効きになるので、配置することが出来ない
template<int NQ>
void backtrackingBitmapS()
{
g_count = 0;
for(uint mask = 1<<(NQ/2-1); mask; mask>>=1) {
g_row[0] = mask;
backtrackingBitmapS<NQ>(mask<<1, mask, mask>>1, 1);
}
}- 1行目角にクイーンがある場合、とそうでない場合で処理を分ける
template<int NQ>
void backtrackingBitmapS()
{
g_count = 0;
for(uint mask = 1<<(NQ/2-1); mask; mask>>=1) {
g_row[0] = mask;
if( mask == 1 ) // 角にクイーンを配置した場合
.....
else
.....
}
}- 1行目角にクイーンがある場合、回転対称形チェックを省略することが出来る
- 1行目角にクイーンがある場合、他の角にクイーンを配置することは不可
- 鏡像についても、主対角線鏡像のみを判定すればよい
- 2行目、2列目を数値とみなし、2行目<2列目という条件を課せばよい
// 1行め角にクイーンを配置した場合template<int NQ>
void backtrackingBitmapSCorner(uint lt, uint dn, uint rt,
int n) // 配置済み個数
{
uint flags = ~(lt|dn|rt) & ((1<<NQ)-1);
if( n == NQ - 1 ) {
if( flags ) {
g_row[n] = flags;
++g_count;
}
} else {
if( (1<<n) <= g_row[1] )
flags &= ~2; // 主対角線鏡像を枝刈り
while( flags ) {
uint bit = -flags & flags;
flags ^= bit;
g_row[n] = bit;
backtrackingBitmapSCorner<NQ>((lt|bit)<<1, (dn|bit), (rt|bit)>>1, n+1);
}
}
}
template<int NQ>
void backtrackingBitmapS()
{
g_count = 0;
for(uint mask = 1; mask < (1<<NQ/2); mask<<=1) {
g_row[0] = mask;
if( mask == 1 ) {
uint flags = ((1<<NQ-1) - 1) ^ 3;
while( flags ) {
uint bit = -flags & flags;
flags ^= bit;
g_row[1] = bit;
backtrackingBitmapSCorner<NQ>((bit<<1)|(1<<2), bit|1, bit>>1, 2);
}
} else
.....
}
}- 1行目角にクイーンが無い場合、クイーン位置より右位置の8対称位置にクイーンを置くことはできない
- 置いた場合、回転・鏡像変換により得られる状態のユニーク判定値が明らかに大きくなる
☓☓☓・・Q☓☓☓
☓・・・・・・・☓
☓・・・・・・・☓
c・・・・・・・rt
・・・・・・・・・
lt・・・・・・・a
☓・・・・・・・☓
☓・・・・・・・☓
☓☓☓b・dn☓☓☓
uint g_prohibit; // 配置可能位置フラグ
template<int NQ>
void backtrackingBitmapSEdge(uint lt, uint dn, uint rt,
int n) // 配置済み個数
{
uint flags = ~(lt|dn|rt) & ((1<<NQ)-1);
if( n == NQ - 1 ) {
flags &= g_prohibit;
if( flags ) {
g_row[n] = flags;
if( symmetryCheck<NQ>() ) {
++g_count;
}
}
} else {
if( !((1<<n) & g_prohibit) )
flags &= ~(1|(1<<NQ-1));
while( flags ) {
uint bit = -flags & flags;
flags ^= bit;
g_row[n] = bit;
backtrackingBitmapSEdge<NQ>((lt|bit)<<1, (dn|bit), (rt|bit)>>1, n+1);
}
}
} template<int NQ>
void backtrackingBitmapS2()
{
g_count = 0;
for(uint mask = 1; mask < (1<<(NQ/2)); mask<<=1) {
g_row[0] = mask;
if( mask == 1 ) {
.....
} else {
g_prohibit = mask - 1;
g_prohibit |= reverse<NQ>(g_prohibit);
g_prohibit = ~g_prohibit; // 配置可能フラグ
backtrackingBitmapSEdge<NQ>(mask<<1, mask, mask>>1, 1);
}
}
}| N | ユニーク解数 | 末端ノード数 | 枝刈(ミリ秒) | Uniq(ミリ秒) | 解数 | 末端ノード数 | Bitmap |
|---|---|---|---|---|---|---|---|
| 4 | 1 | 2 | 0 | 0 | 2 | 6 | 0 |
| 5 | 2 | 5 | 0 | 0 | 10 | 14 | 0 |
| 6 | 1 | 15 | 0 | 0 | 4 | 50 | 0 |
| 7 | 6 | 59 | 0 | 0 | 40 | 194 | 0 |
| 8 | 12 | 212 | 0 | 0 | 92 | 736 | 0 |
| 9 | 46 | 807 | 0 | 1 | 352 | 2,936 | 0 |
| 10 | 92 | 3,479 | 0 | 0 | 724 | 12,774 | 0 |
| 11 | 341 | 16,225 | 0 | 3 | 2,680 | 61,076 | 2 |
| 12 | 1,787 | 82,940 | 4 | 14 | 14,200 | 314,730 | 10 |
| 13 | 9,233 | 443,353 | 16 | 79 | 73,712 | 1,716,652 | 50 |
| 14 | 45,752 | 2,563,413 | 80 | 449 | 365,596 | 10,030,692 | 298 |
| 15 | 285,053 | 15,704,793 | 480 | 3,001 | 2,279,184 | 62,518,772 | 1,805 |
| 16 | 1,846,955 | 103,176,096 | 3,216 | 20,142 | 14,772,512 | 415,515,376 | 12,179 |
| 17 | 11,977,939 | 713,303,685 | 21,984 | N/A | N/A | N/A | N/A |
| 18 | 83,263,591 | 5,224,009,865 | 163,225 | N/A | N/A | N/A | N/A |
- ユニーク解数を得るための枝刈りにより、末端局面数が大幅に減り、処理時間も6倍程度高速になった
- 解総数を求めるビットマップ法に比べても約4倍高速である
- 探索速度:約5.7*10^6 NPS
さいごに
-
N-Queens 問題を4種のアルゴリズム/データ構造で記述し、パフォーマンス計測を行った
-
ビットマップを用いるバックトラッキングが予想以上に高速であった
-
N-Queens 問題の分析に基づく枝刈りにより、さらなる高速化が達成できた
-
N-Queens 問題は単純な探索問題だと思っていたが、予想外に奥が深く、びっくりしたでござる
参考文献
- ビットマップを N-Queens に最初に応用したのは Jeff Somers 氏のようだ。
参照: The N Queens Problem
-
対称解の除去方法については、takaken氏による詳しい解説がある
参照: Nクイーン問題(解の個数を求める)
-
2004年、電気通信大学の研究グループが、処理を並列化し、N=24 の解の個数を世界で初めて発見。
参照: N-queens Homepage in Japanese
参照:
NQueens問題
参照:対称解の特性を用いた N-Queens 問題の求解とGPU による高速化
(情報処理学会研究報告 2012/03)
ご清聴ありあとうございまする
m(_ _)m
N-Queens 問題
By Nobuhide Tsuda
N-Queens 問題
- 4,300




