Estática

Unidad 1: Vectores en dos y tres dimensiones

Facultad de Ingeniería/Campus Mexicali

Ing. Oscar Alonso Rosete Beas

Sesion 13 Rev:2 ciclo 2020-1

Sesiones Previaa

• Vectores unitarios

• Conceptos básicos

• Representación fuerza 2D

• Suma y resta vectorial (fuerza resultante): Métodos gráficos del paralelogramo, triangulo, polígono

• Diagrama de cuerpo libre

• Descomposición de una fuerza.

  • 1.6 vectores unitarios.

  • 1.7 resultante aplicando ley de senos, ley de cosenos y el de componentes rectangulares.

  • 1.8 Equilibrio de una partícula: línea de acción, fuerzas concurrentes, diagrama de cuerpo libre y polígono cerrado.

Agenda

Unidad 1: Vectores en dos y tres dimensiones

• 1.9 Componentes en tres dimensiones: cosenos directores y su interpretación gráfica.

• 1.10 Vector posición en función de sus componentes.

• 1.11 Equilibrio de una partícula en el espacio.

   

Ejemplo profesor

Estática 9. Beer

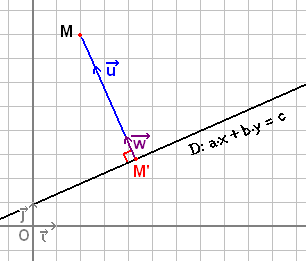
La distancia mínima se ubica en la proyección ortogonal del punto M sobre D, es decir, el punto M' de la recta D tal que (MM') sea perpendicular a ella

Sugerencia rotar la linea a horizontal.

Ejercicio alumno

Ingenieria mecánica estática 12. Hibbeler

Geometría en 3 dimensiones

Sistema coordenado derecho

Se dice que un sistema coordenado rectangular es derecho si el pulgar de la mano derecha señala en la dirección del eje z positivo, cuando los dedos de la mano derecha se curvan alrededor de este eje y están dirigidos del eje x positivo hacia el eje y positivo.

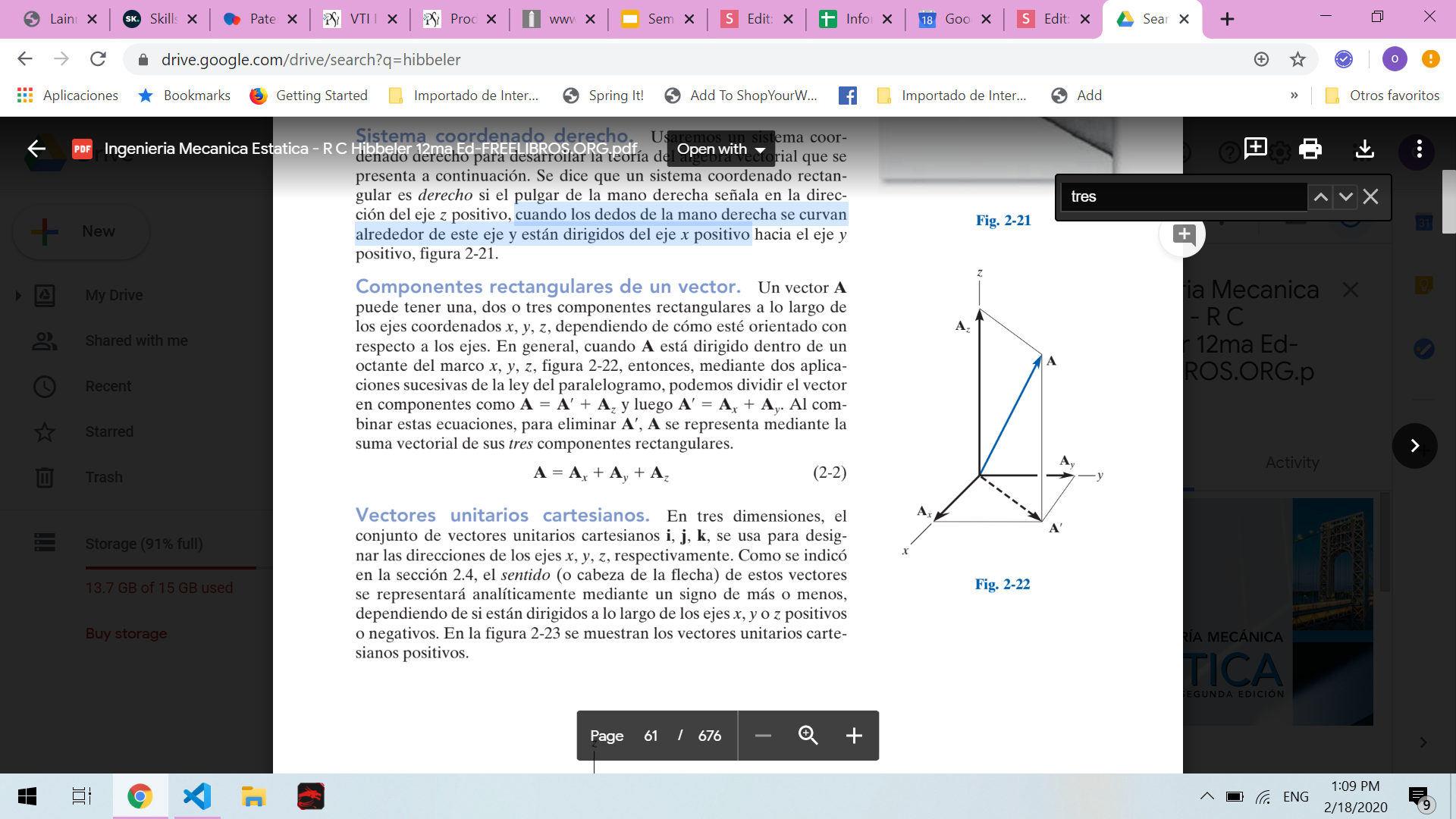
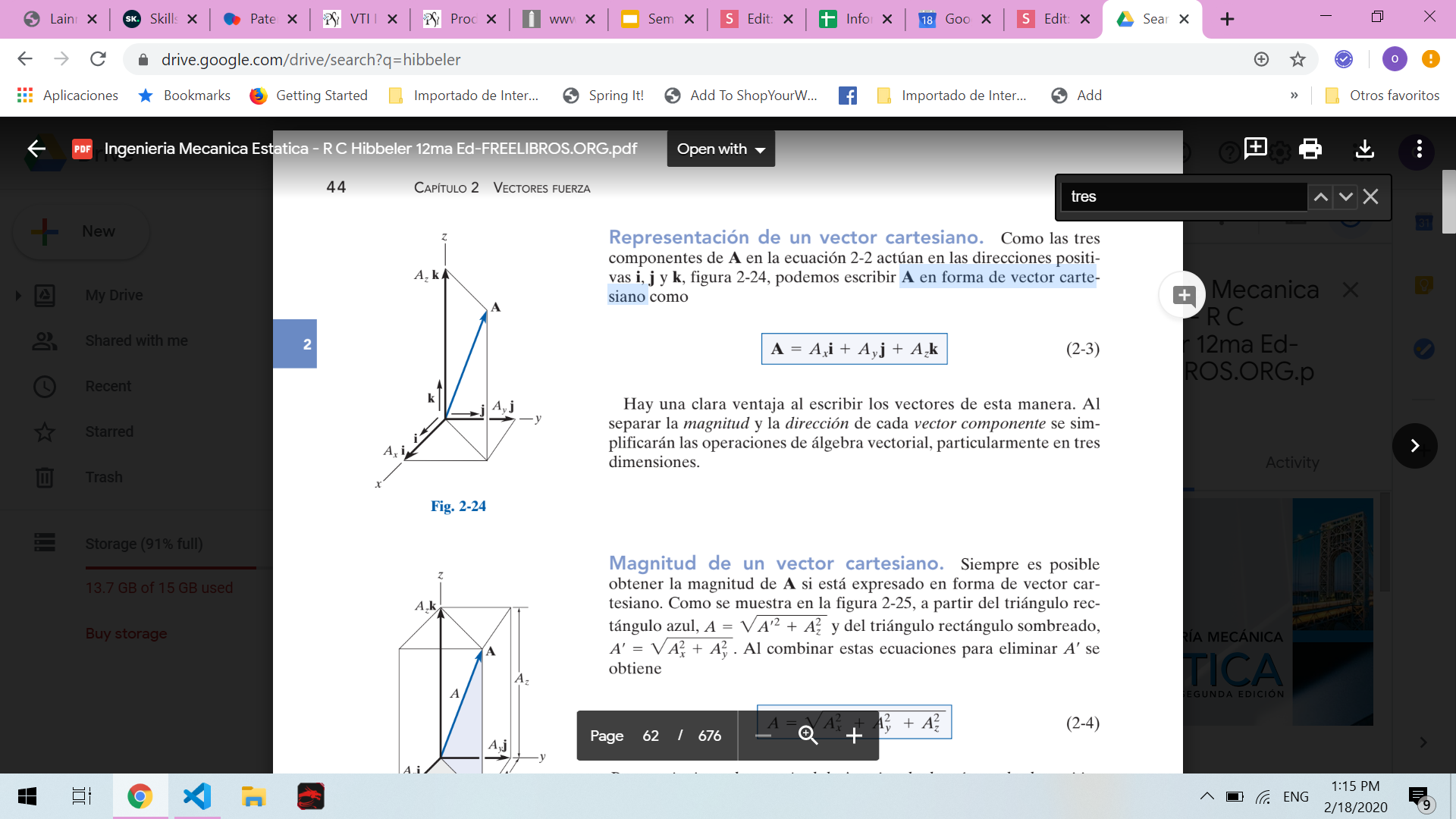
Componentes rectangulares de un vector

Un vector A puede tener una, dos o tres componentes rectangulares a lo largo de los ejes coordenados x, y, z.

A = Ax + Ay+ Az

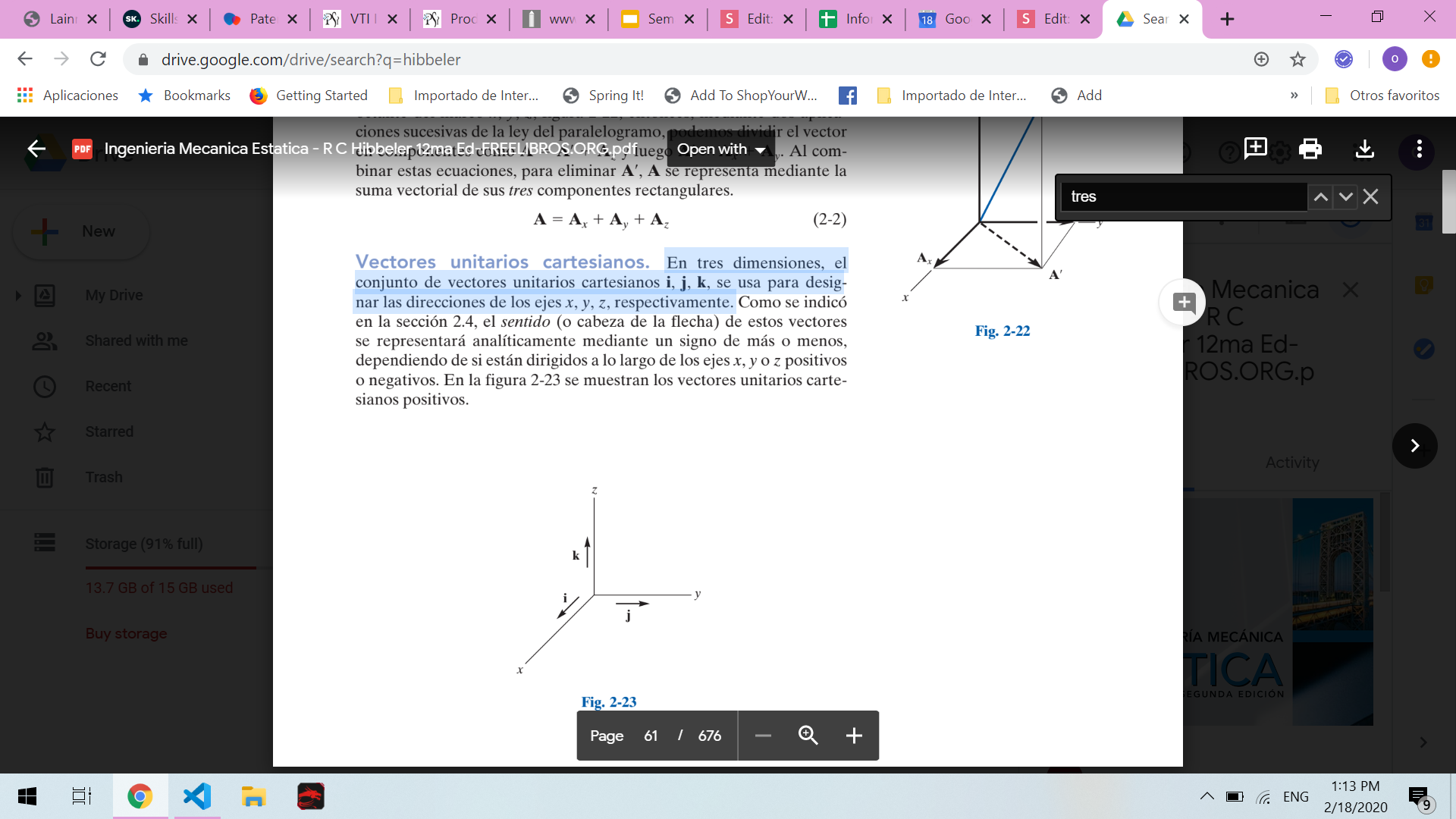
Vectores unitarios cartesianos

En tres dimensiones, el conjunto de vectores unitarios cartesianos i, j, k, se usa para designar las direcciones de los ejes x, y, z, respectivamente.

A en forma de vector cartesiano

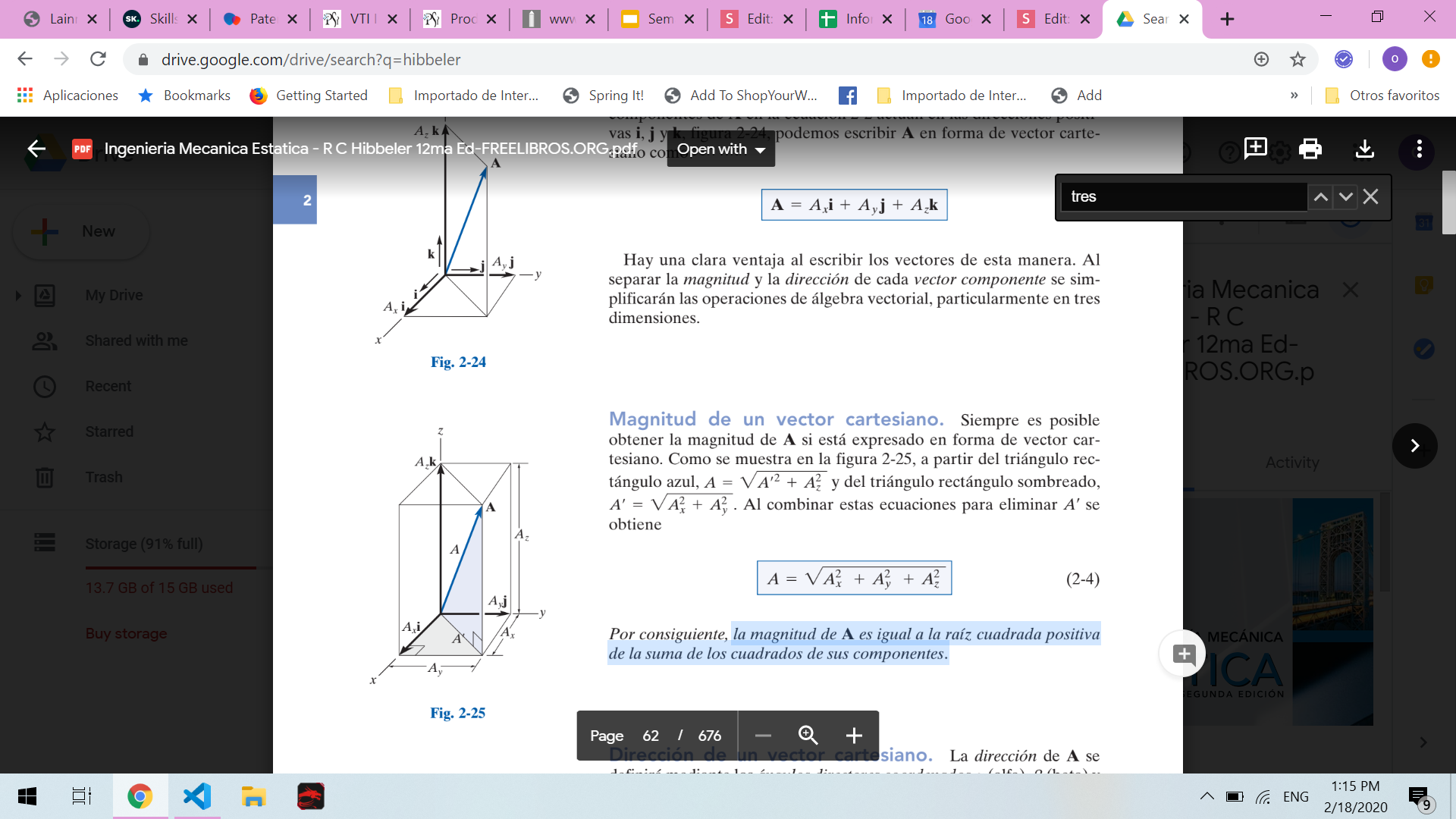
Magnitud de un vector en el espacio

La magnitud de A es igual a la raíz cuadrada positiva de la suma de los cuadrados de sus componentes.

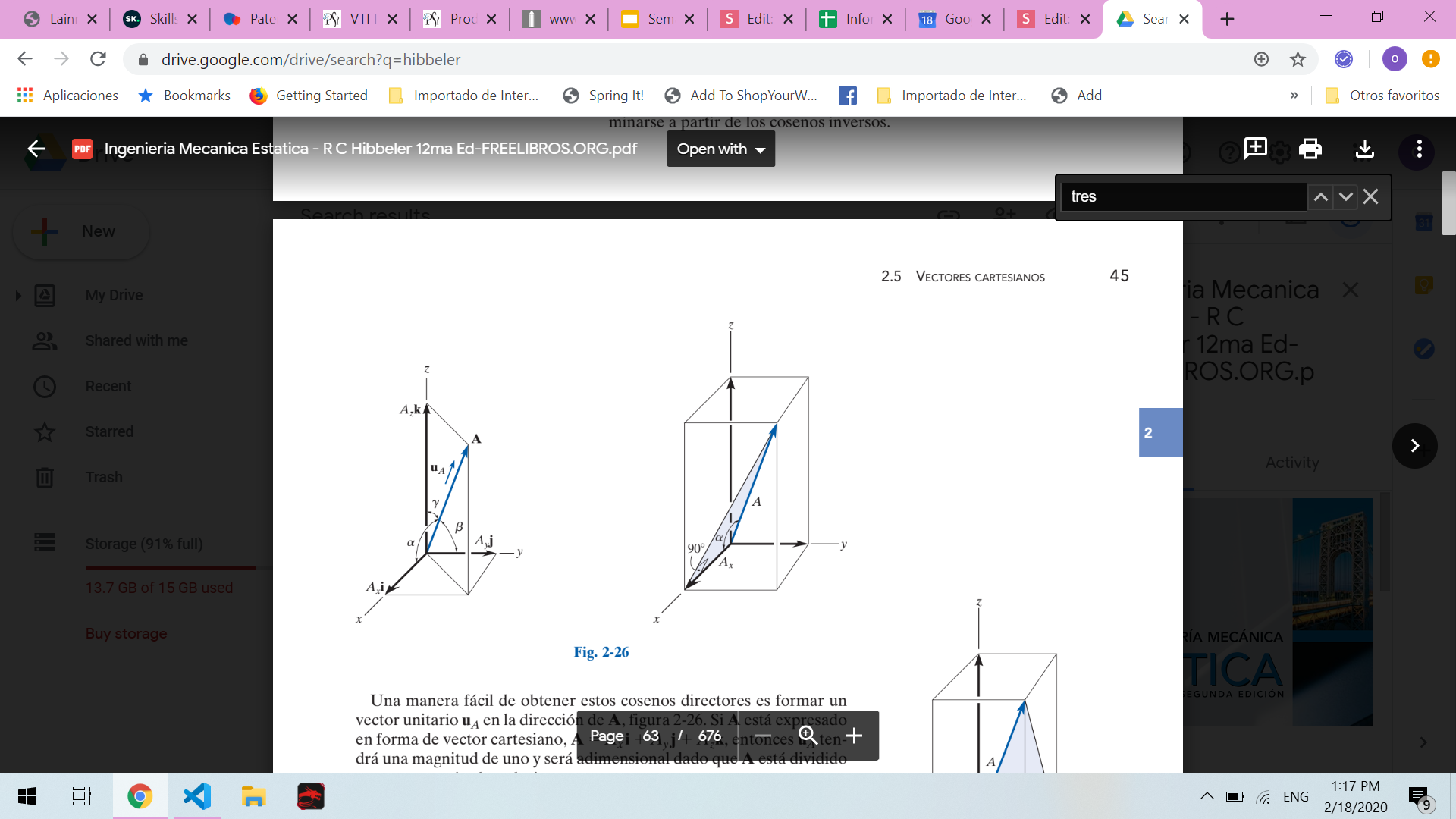
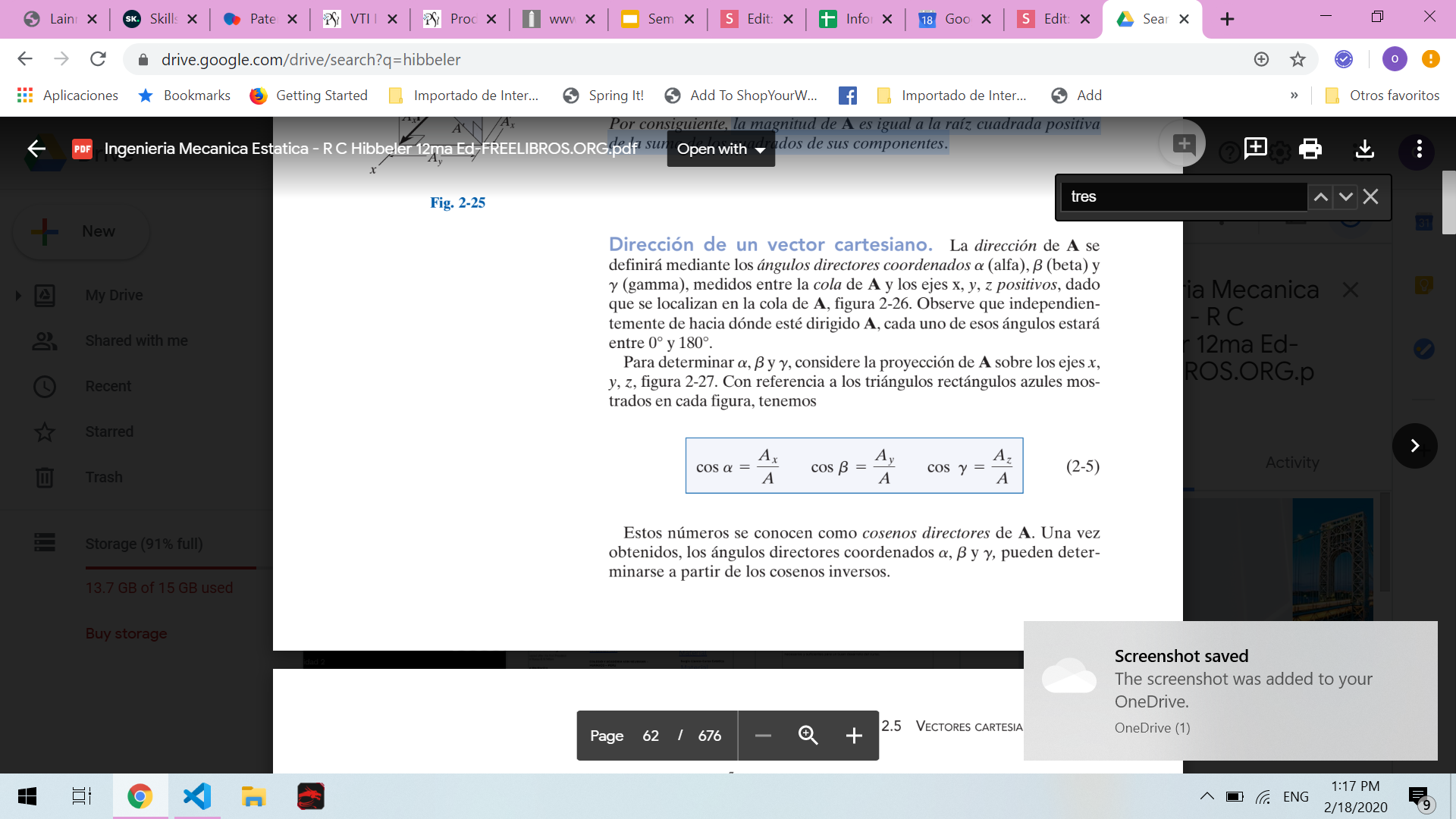
Dirección de un vector en el espacio

La dirección de A se definirá mediante los ángulos directores coordenados a (alfa), b (beta) y g (gamma), medidos entre la cola de A y los ejes x, y, z positivos, dado que se localizan en la cola de A.

Observe que independientemente de hacia dónde esté dirigido A, cada uno de esos ángulos estará entre 0° y 180°.

Ejemplo profesor

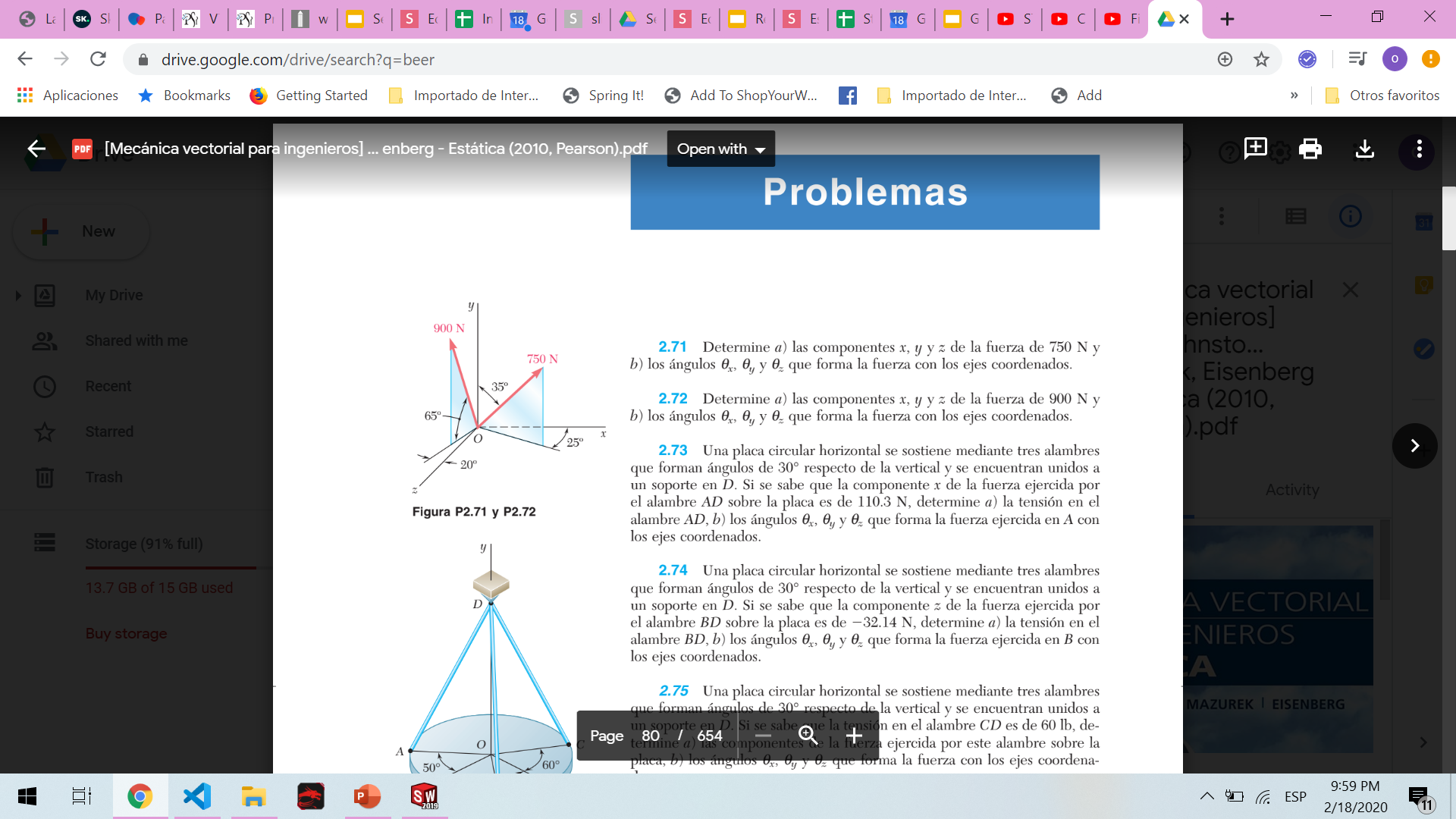
Estática 9. Beer

Ejercicio alumno

Estática 9. Beer

Ejercicio alumno 2

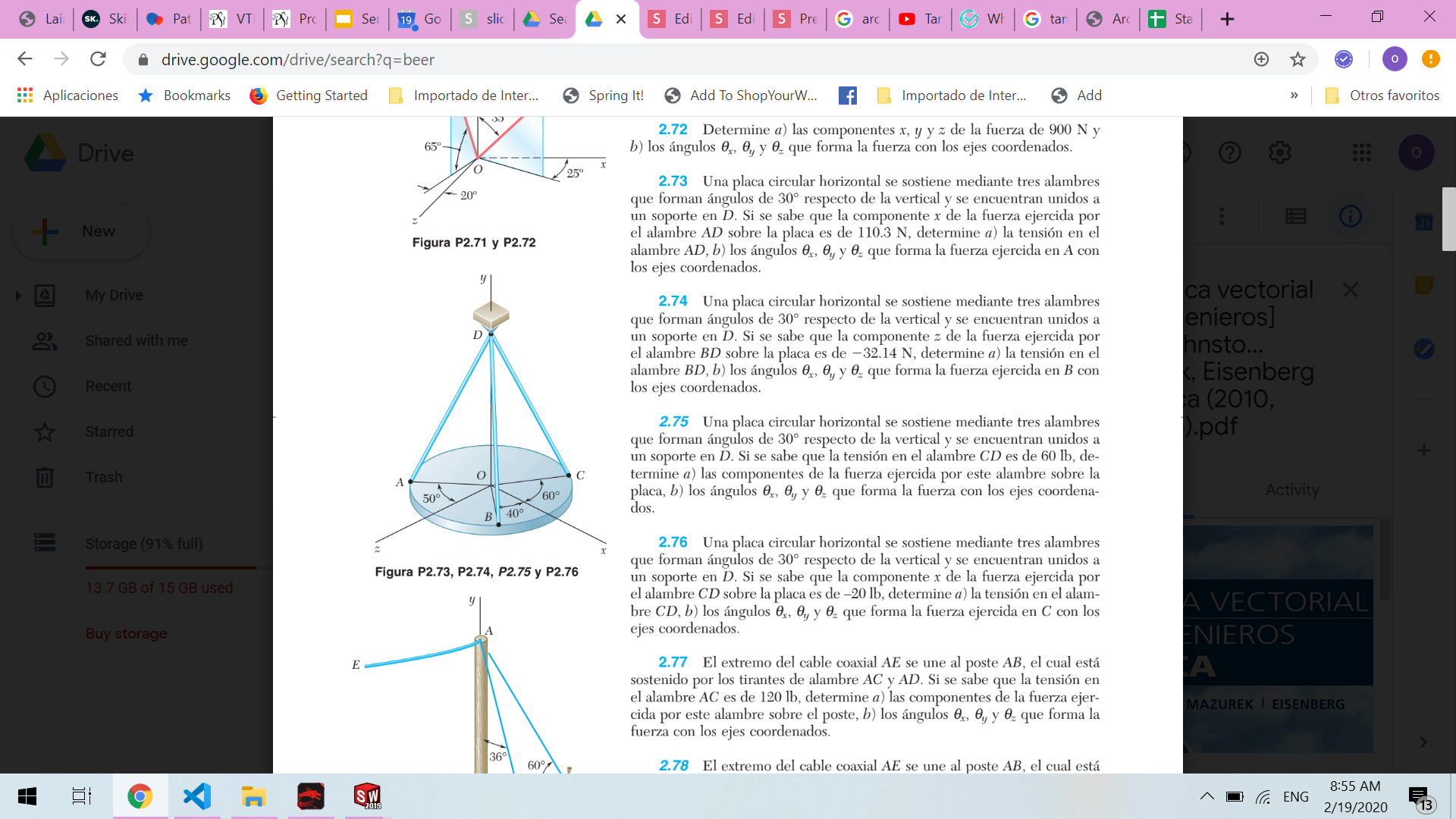
Estática 9. Beer

Componentes rectangulares de un vector