Estática
Unidad 1: Vectores en dos y tres dimensiones
Facultad de Ingeniería/Campus Mexicali
Ing. Oscar Alonso Rosete Beas
Sesion 13 Rev:2 ciclo 2020-1
Sesiones Previaa
-
Vectores unitarios
-
Conceptos básicos
-
Representación fuerza 2D
-
Suma y resta vectorial (fuerza resultante): Métodos gráficos del paralelogramo, triangulo, polígono
-
Diagrama de cuerpo libre
-
Descomposición de una fuerza.
-
1.6 vectores unitarios.
-
1.7 resultante aplicando ley de senos, ley de cosenos y el de componentes rectangulares.
-
1.8 Equilibrio de una partícula: línea de acción, fuerzas concurrentes, diagrama de cuerpo libre y polígono cerrado.
-
Agenda
Unidad 1: Vectores en dos y tres dimensiones
-
1.9 Componentes en tres dimensiones: cosenos directores y su interpretación gráfica.
-
1.10 Vector posición en función de sus componentes..
-
1.11 Equilibrio de una partícula en el espacio.
Calificaciones y asistencias

Ejemplo profesor

Ingenieria mecánica estática 12. Hibbeler


Ejercicio alumno
-
Para entregar, en equipos de 3 inventar, resolver y exponer un problema que conlleve la sumatoria de 3 vectores de fuerza.
- Resolución por método gráfico
- Resolución por método analítico.
Actividad de clase
Exposición 10%
Ejemplo
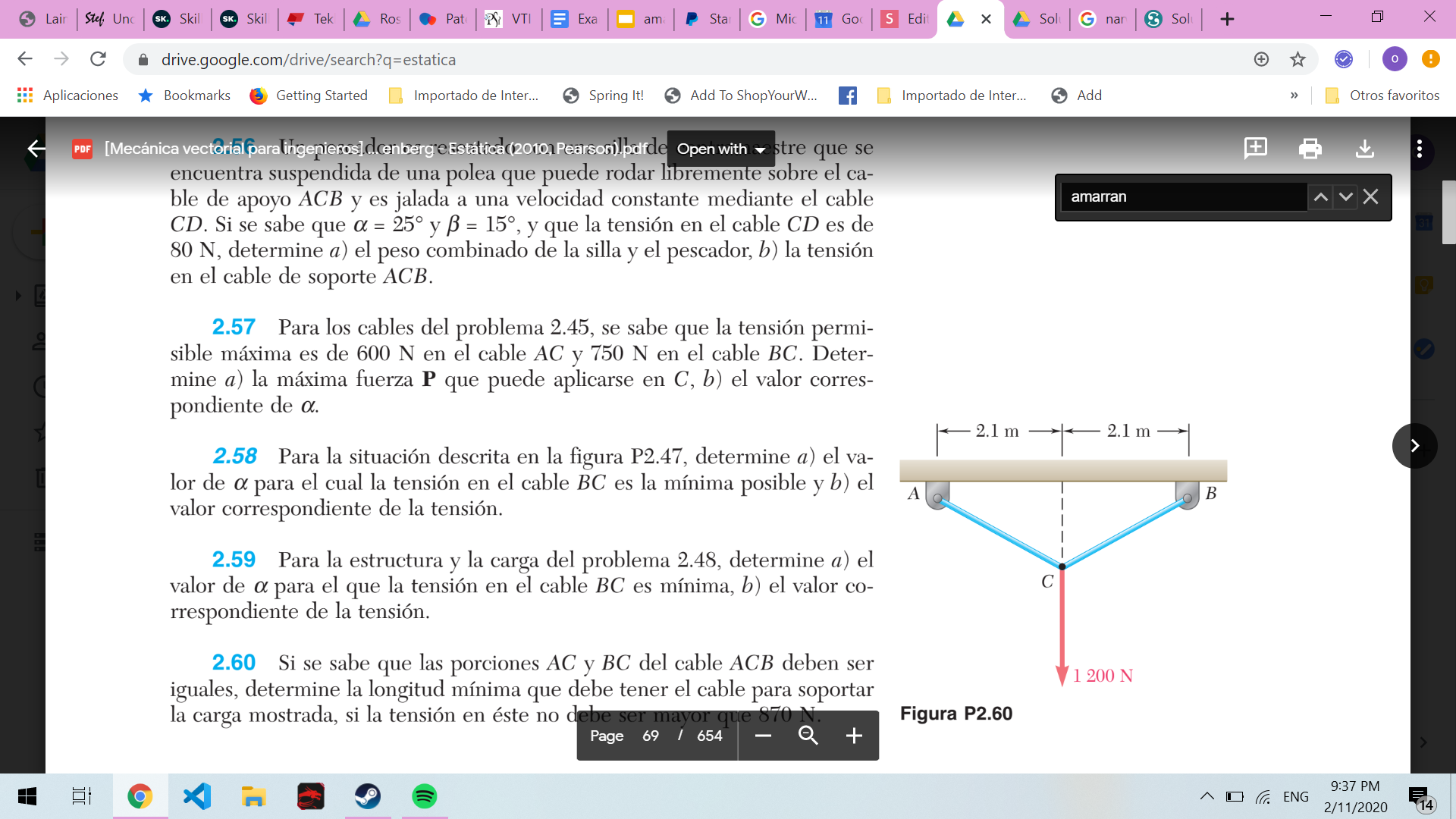
Procedimiento
Ingenieria mecánica estática 12. Hibbeler
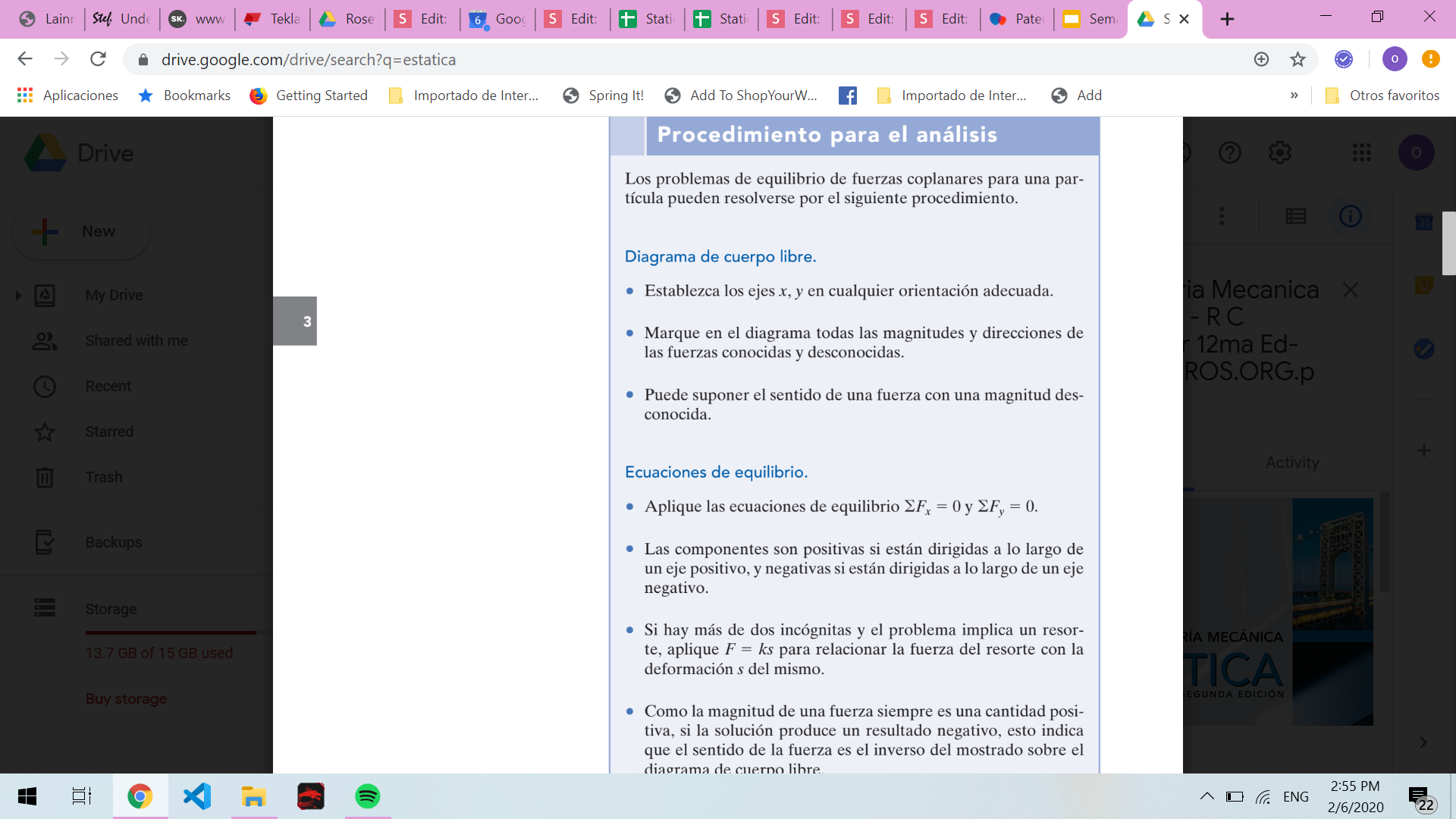

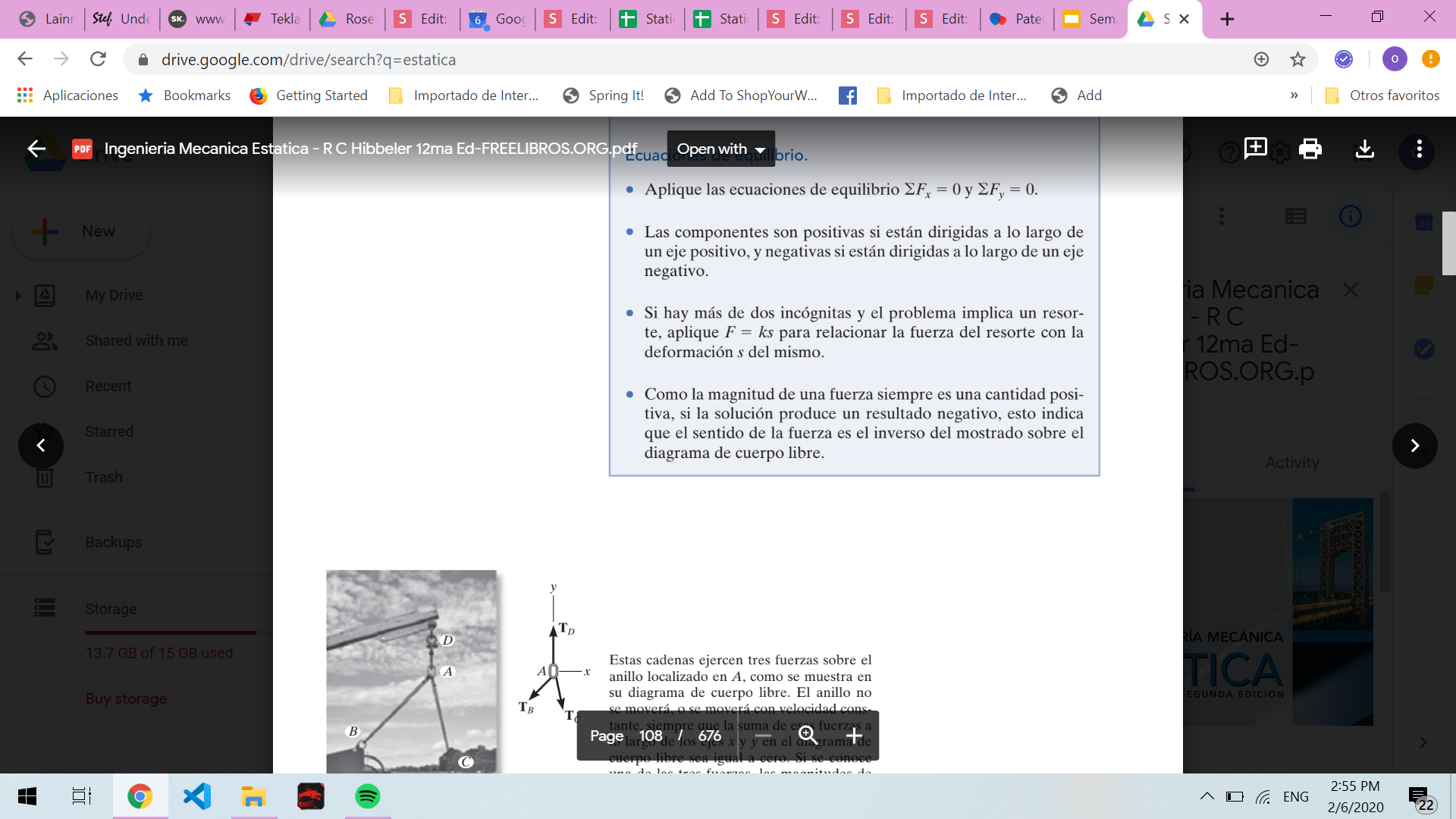
Ingenieria mecánica estática 12. Hibbeler
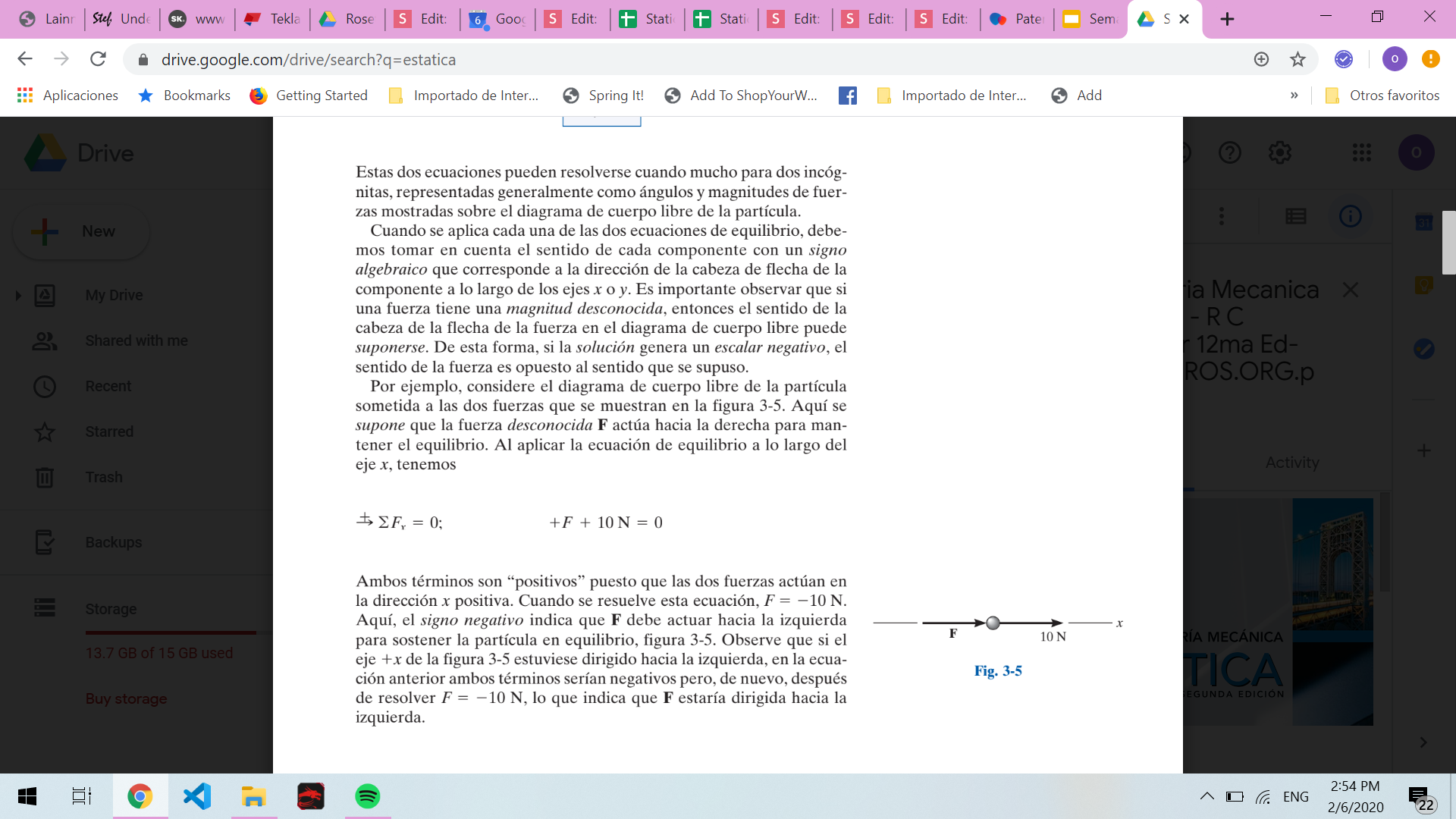
Equilibrio de una partícula 2D
Ejemplo
Ingenieria mecánica estática 12. Hibbeler
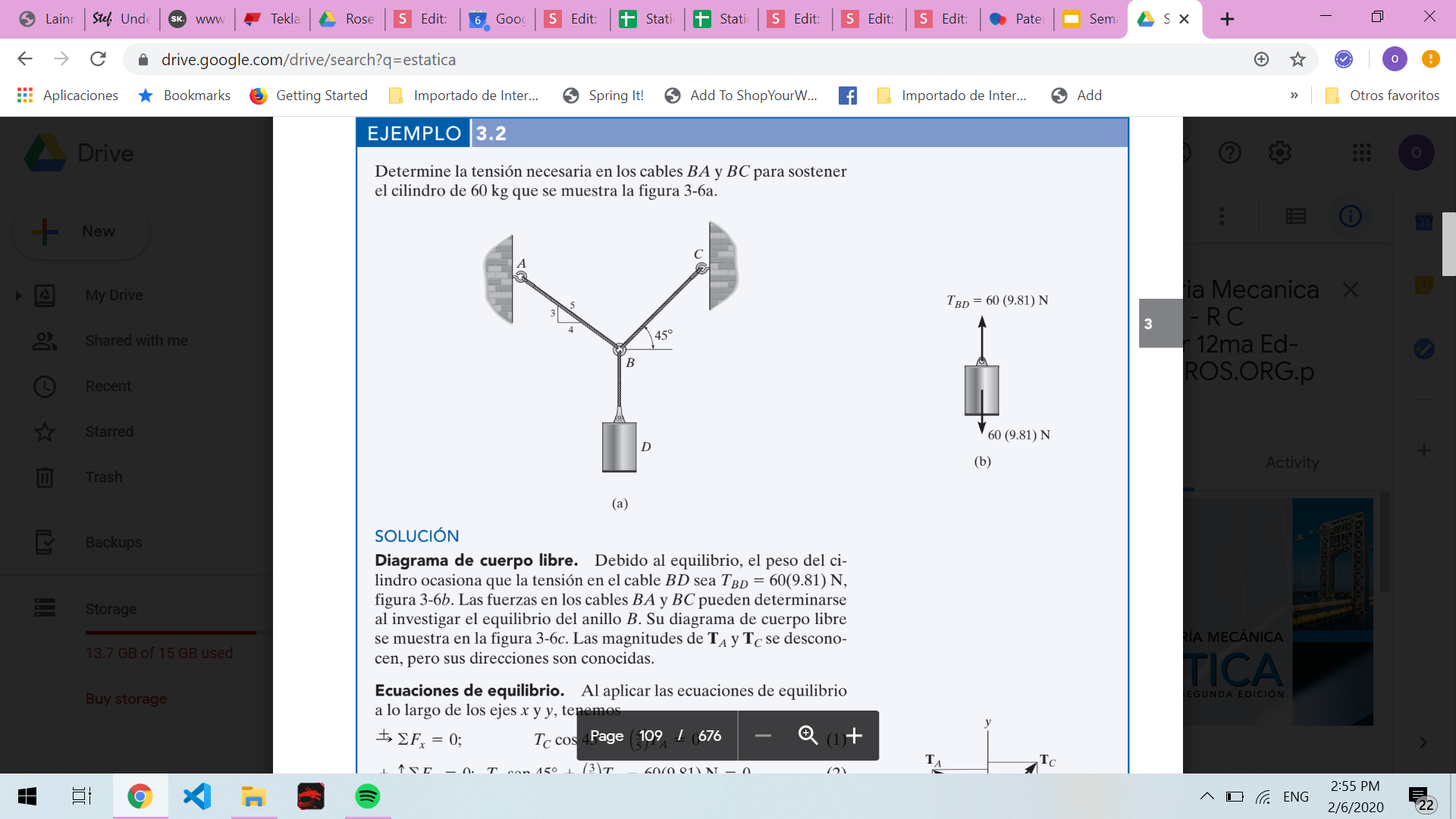
Ejemplo

Ingenieria mecánica estática 12. Hibbeler
Portafolio 4
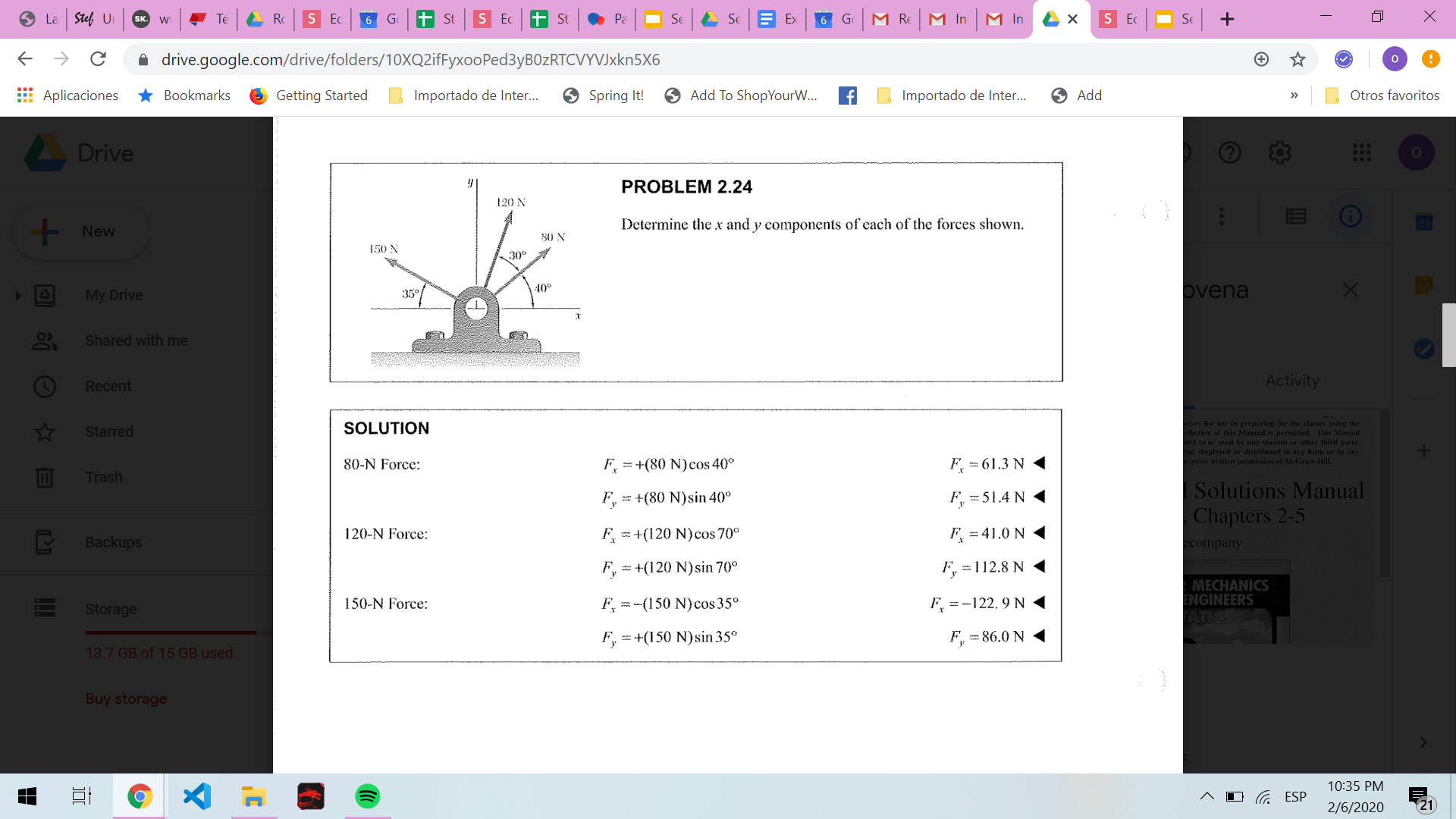
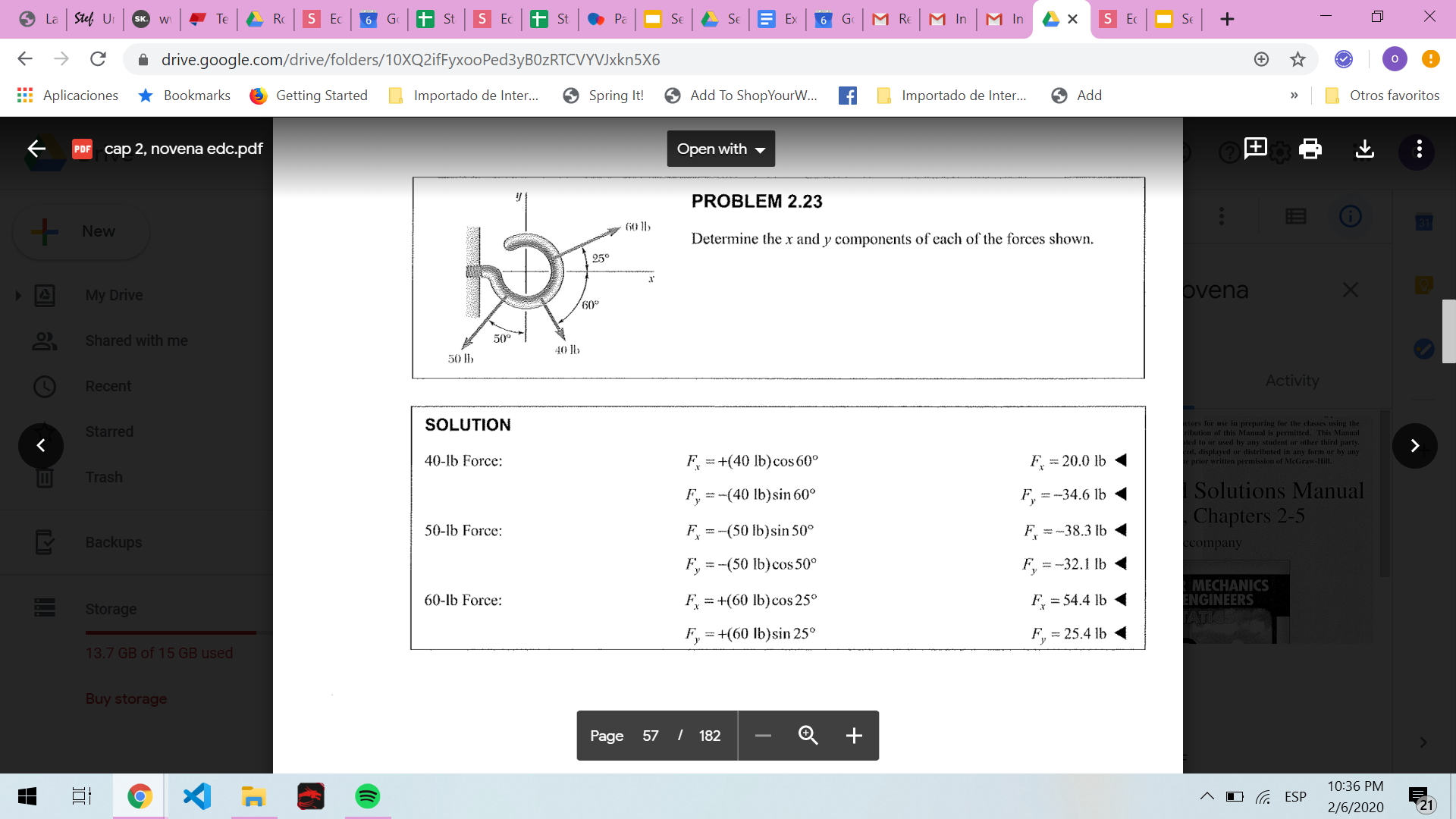
2.23
Portafolio 4
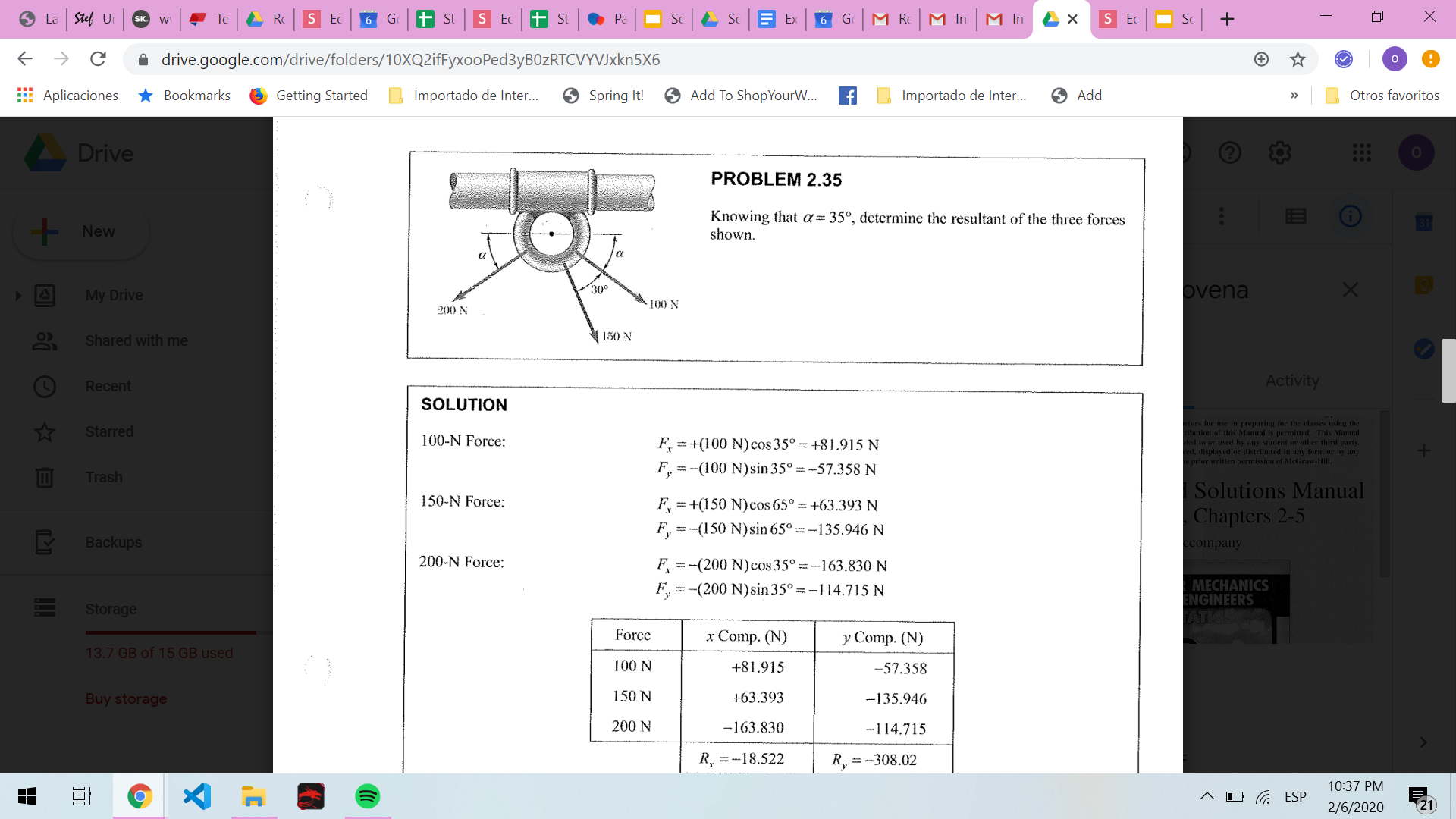
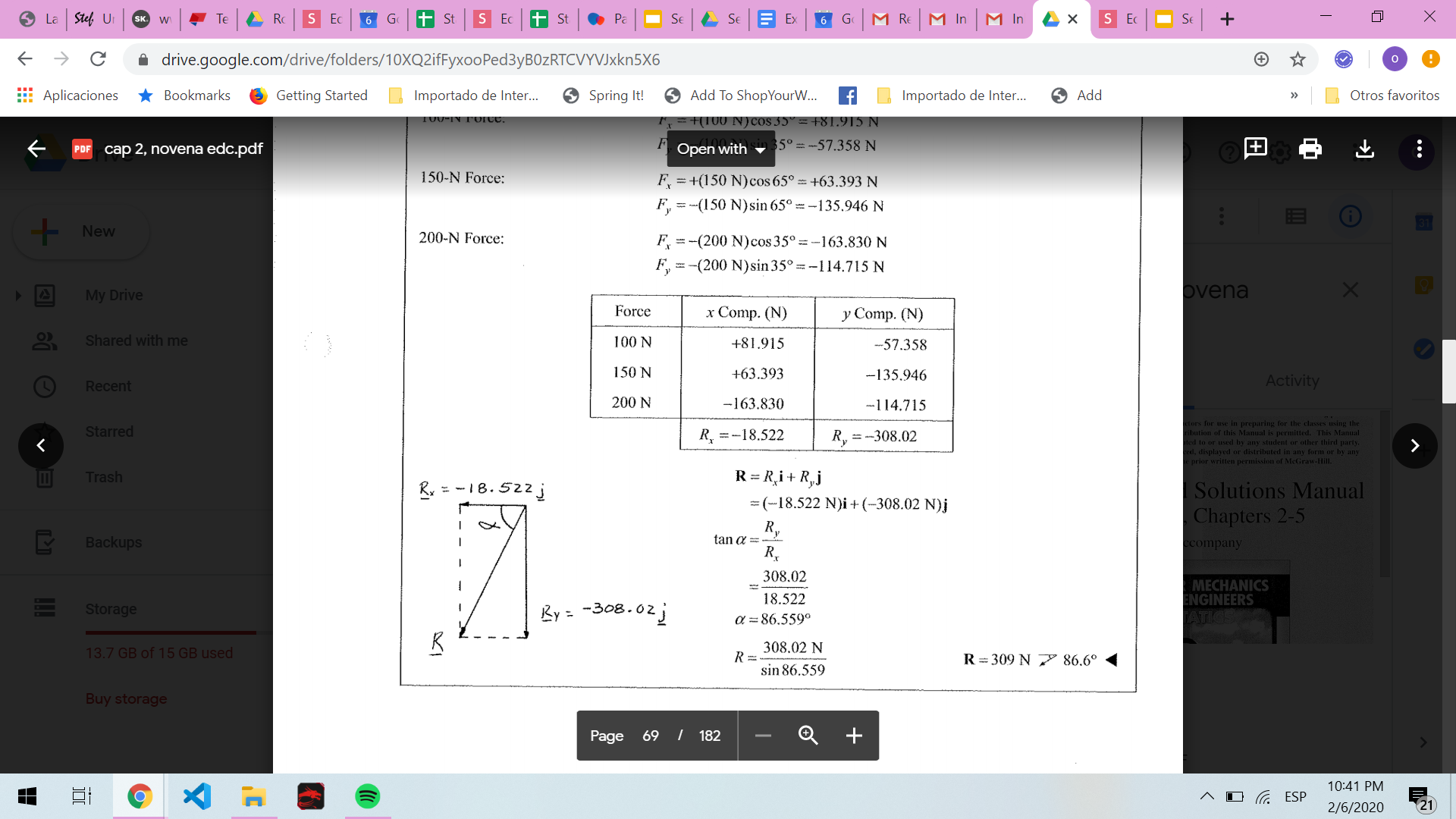
Portafolio 4
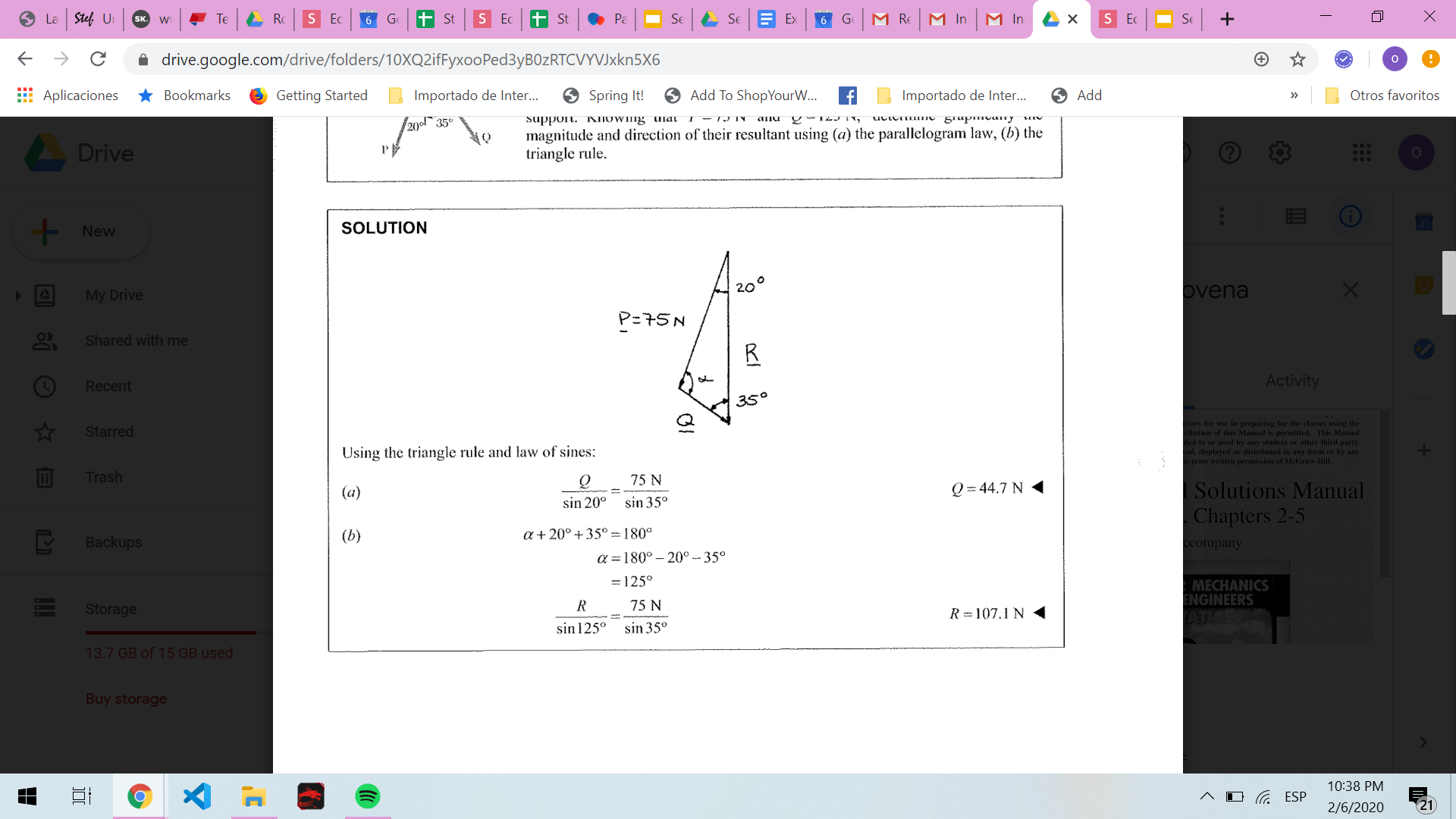
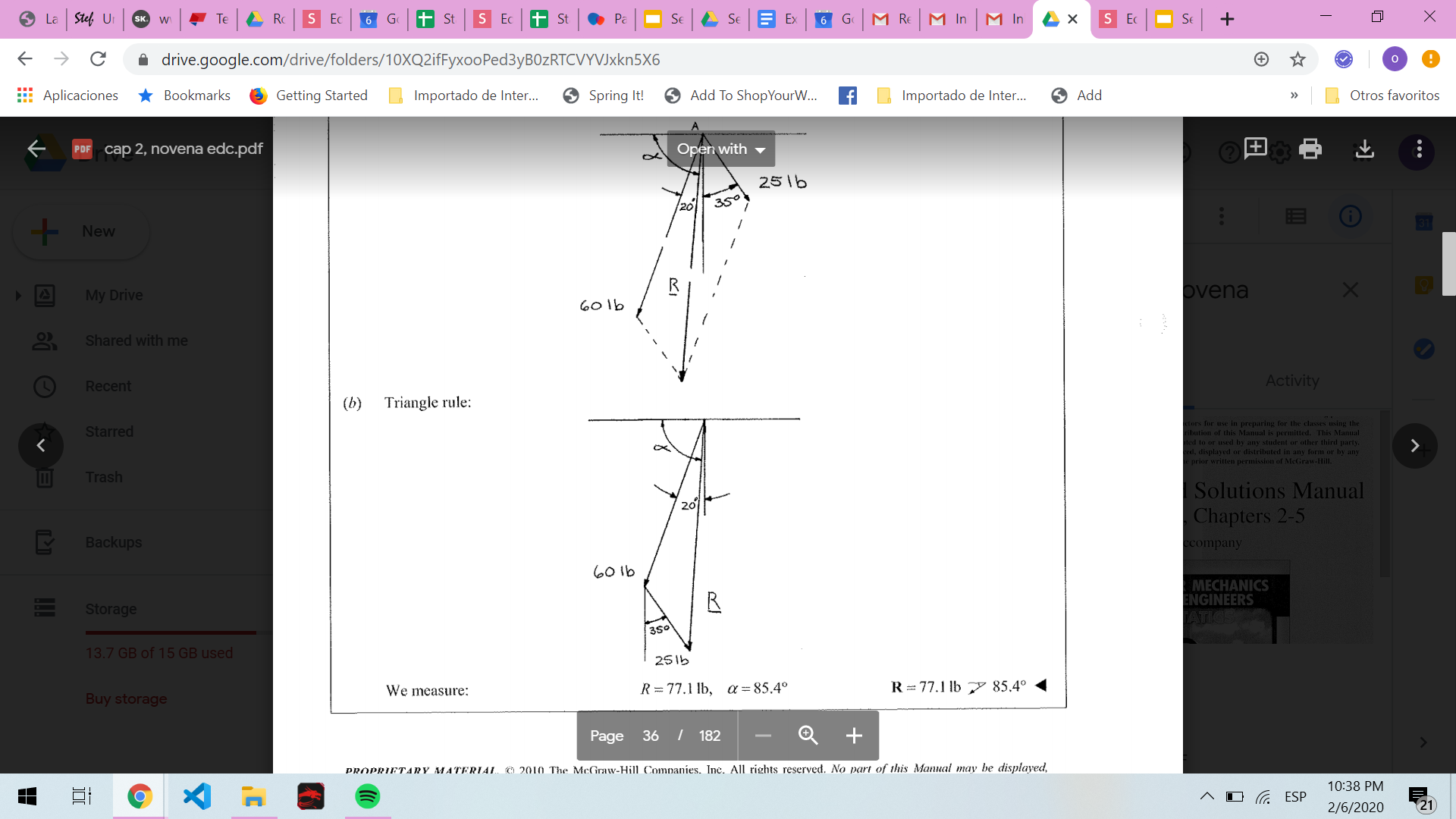
2.2
2.8
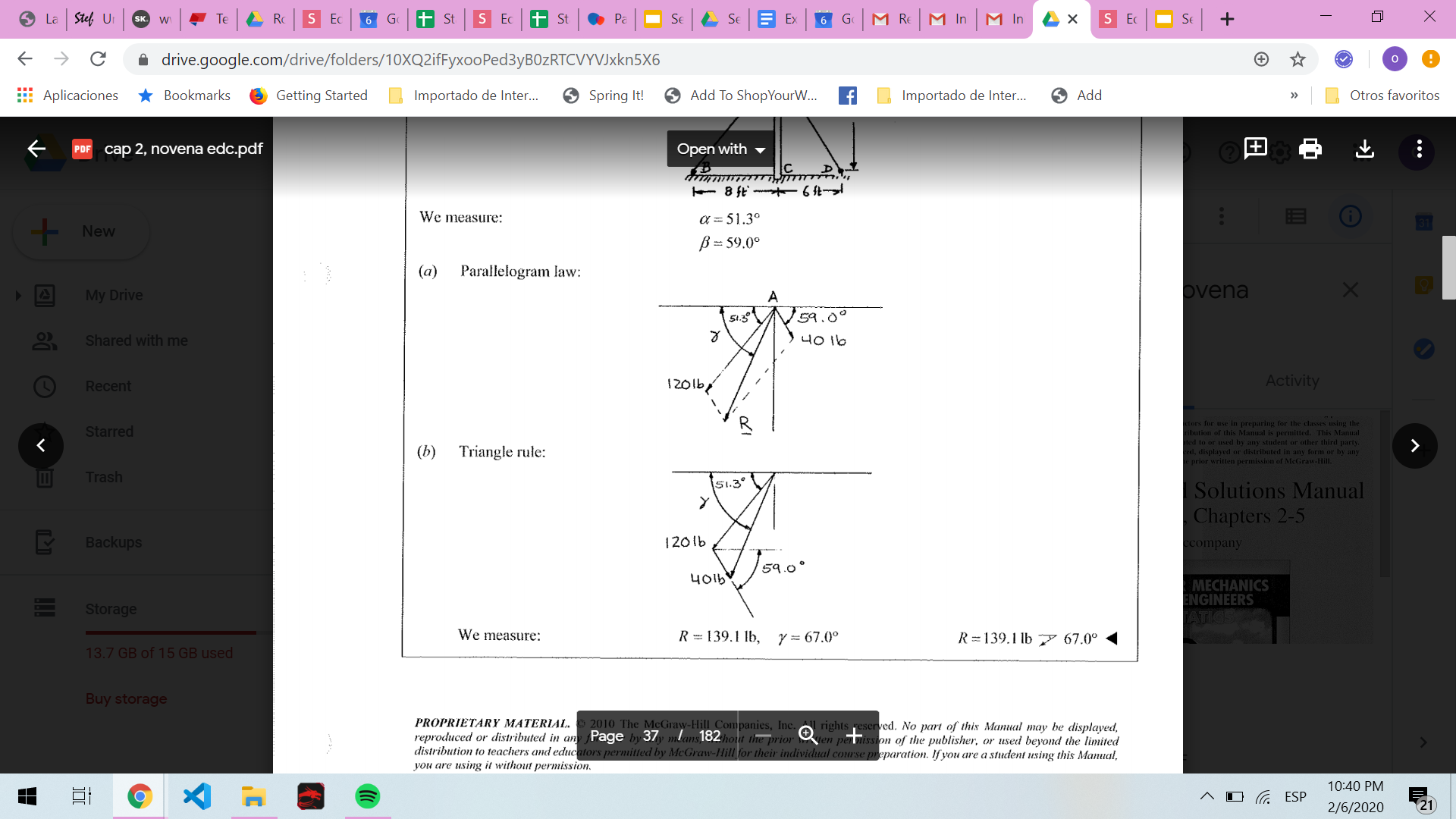
2.3
Portafolio 4


2.2
2.8

2.3
Portafolio 3
Ejercicio ingeniería mecánica estática 12 edición R.C. Hibbeler
Resolución por el método de polígono y comprobación por descomposición
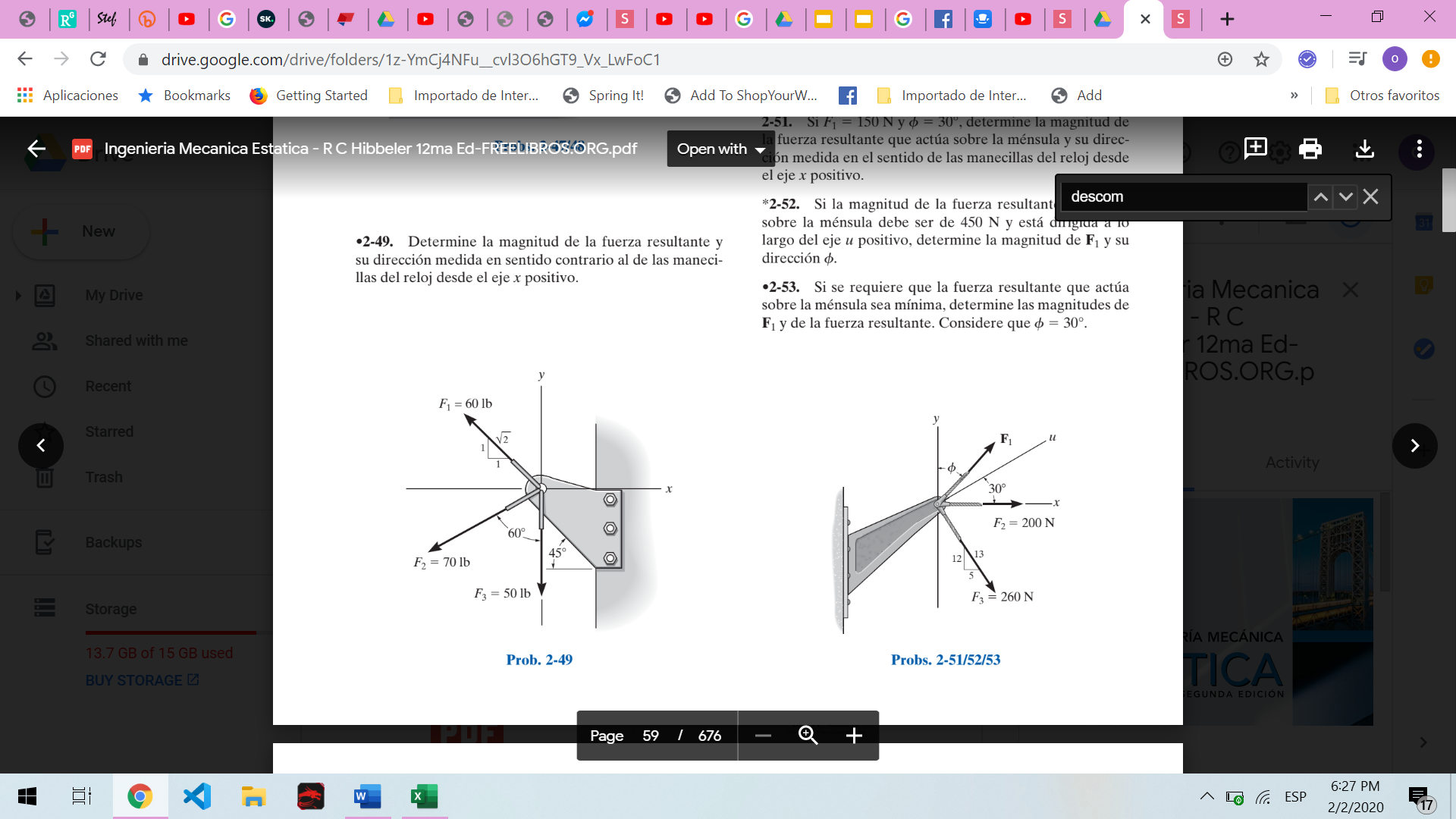

Portafolio 4
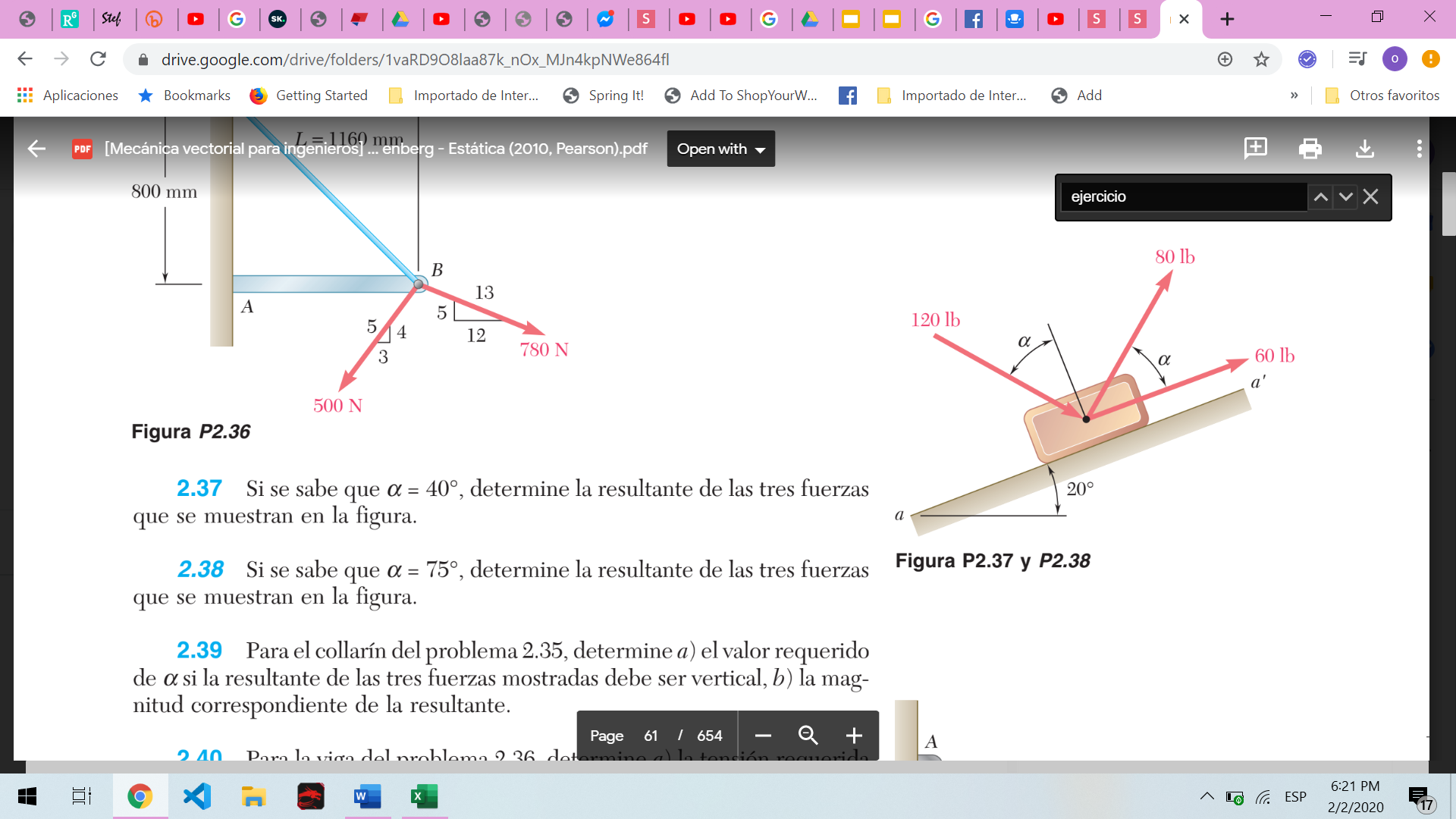
Ejercicio 9na edición E. Russell Johnston and Ferdinand P. Beer
Actividad:
- Resolución por el método de polígono
- Comprobación por descomposición

Notación vectorial cartesiana
Ingenieria mecánica estática 12. Hibbeler
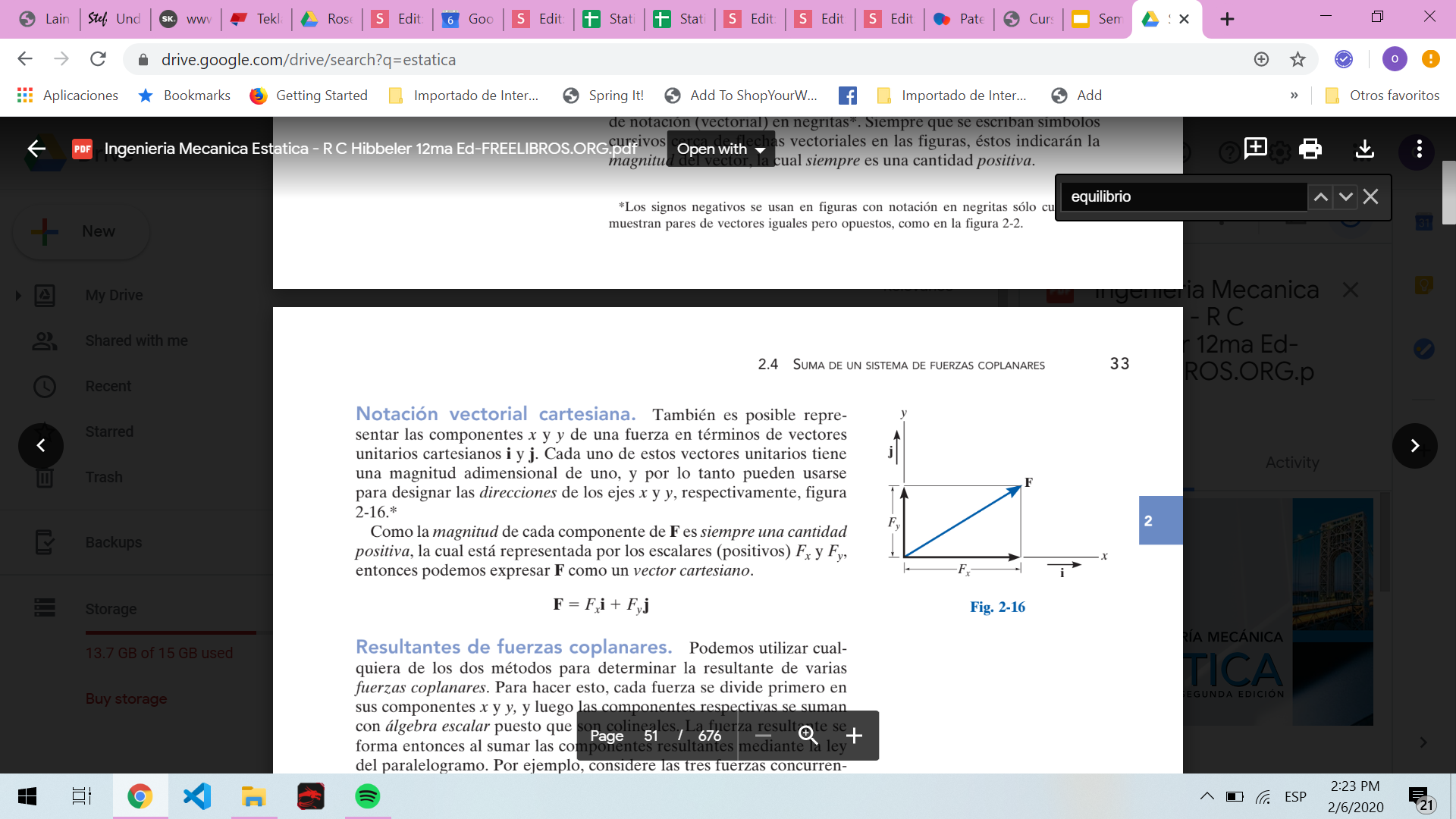
Tambien es posible representar los componentes x y y de una fuerza en terminos de vectores unitarios cartesianos i y j. cada uno de estos vectores unitarios tiene una magnitud adimensional de uno, y por lo tanto pueden usarse para designar las direcciones de los ejecs x y y, respectivamente.

Notación vectorial cartesiana
Ingenieria mecánica estática 12. Hibbeler
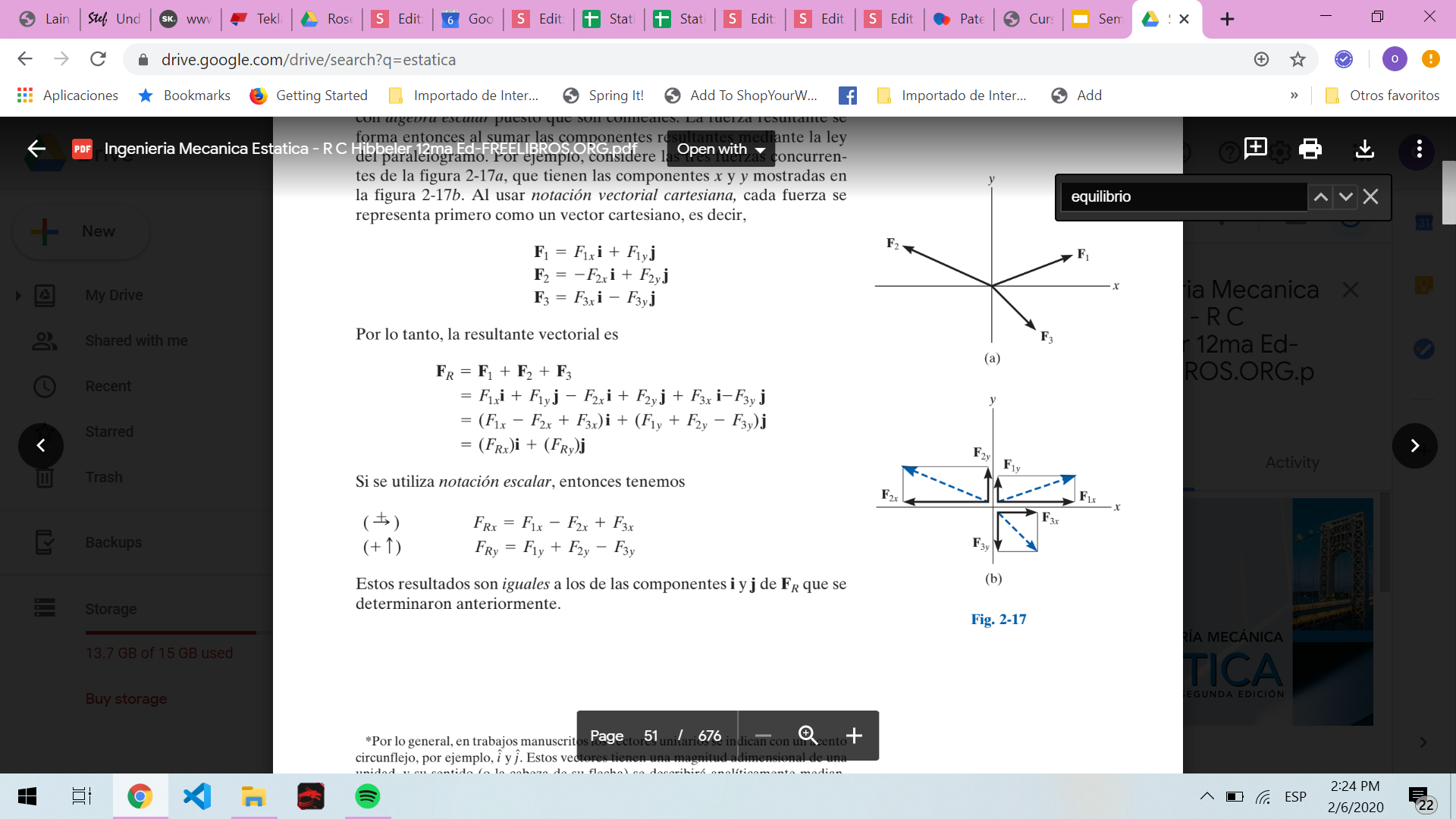

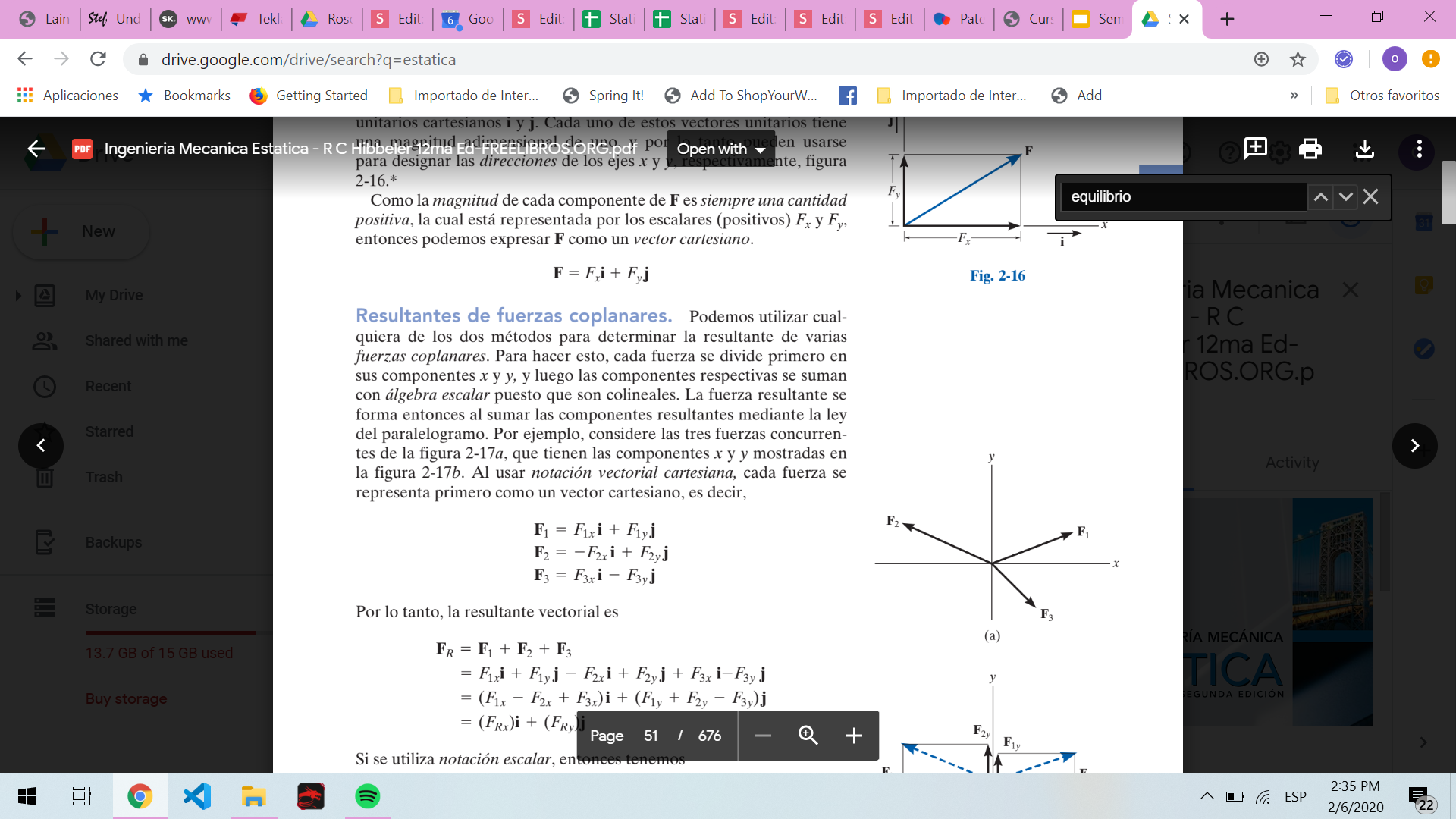
Notación escalar



Ingenieria mecánica estática 12. Hibbeler
Ejemplo representación
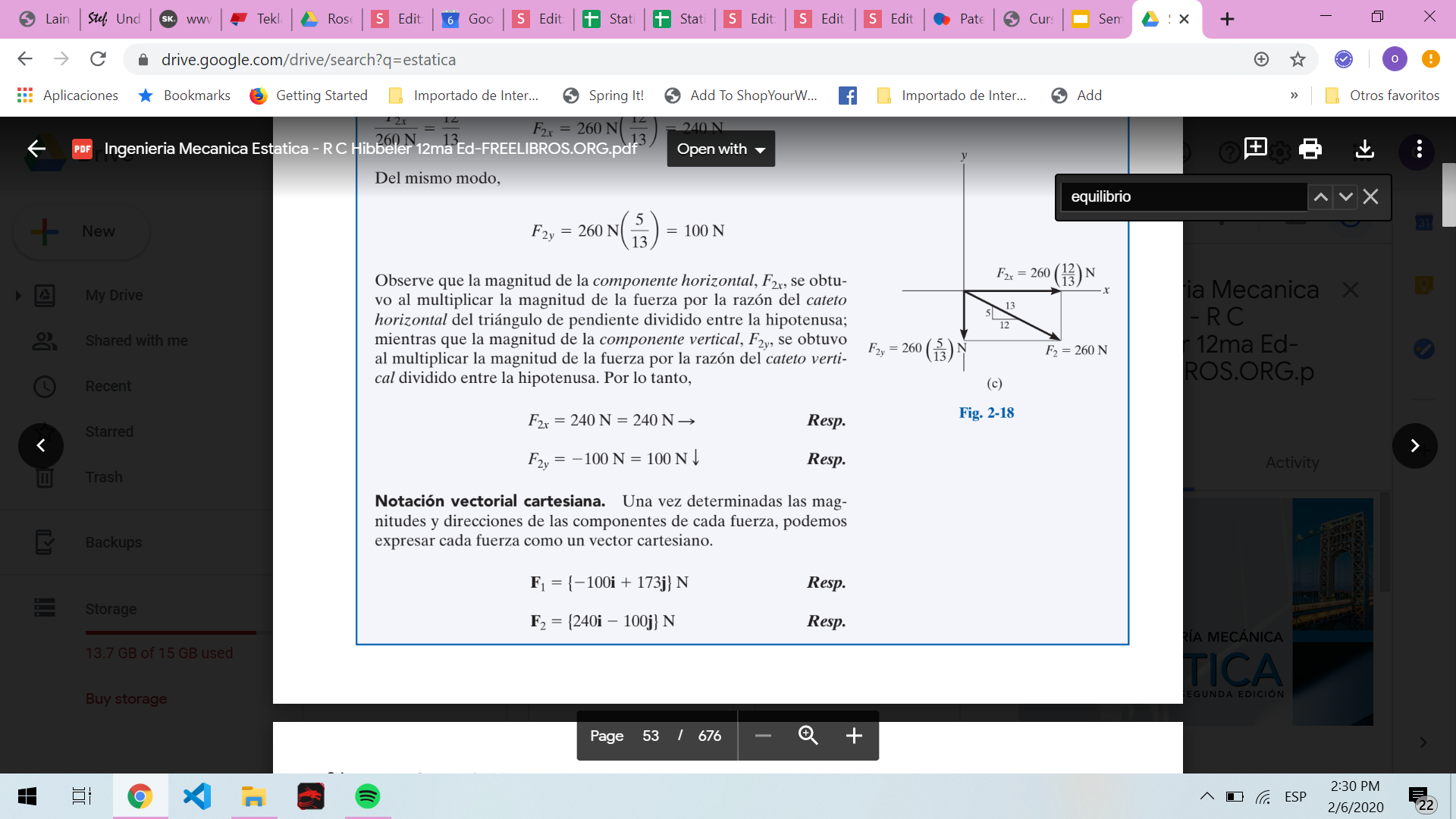
Notación escalar
Notación vectorial cartesiana

Ingenieria mecánica estática 12. Hibbeler
Sumatoria de fuerzas (Fuerza resultante)
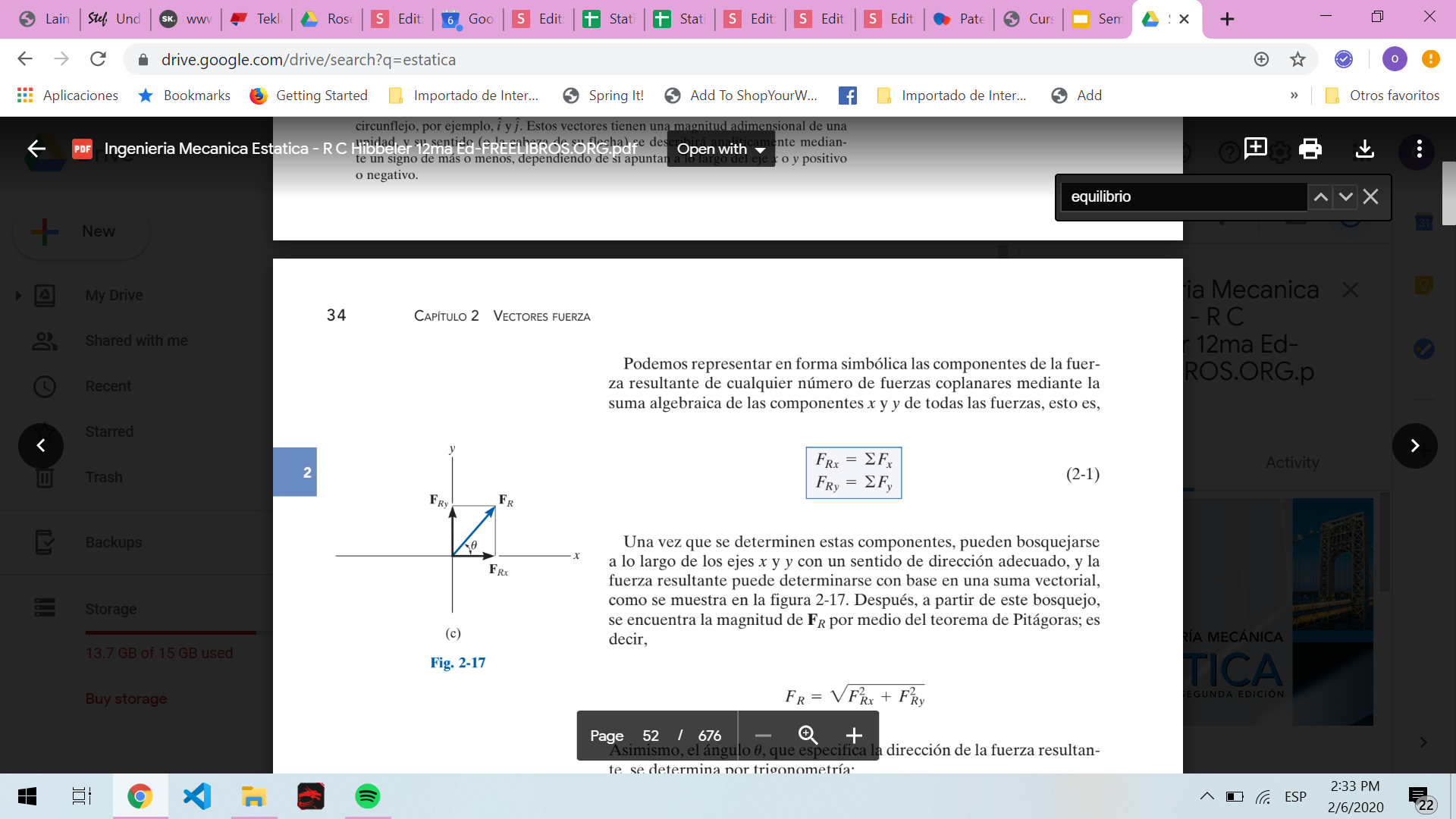
Ingenieria mecánica estática 12. Hibbeler
Podemos representar en forma simbólica las componentes de la fuerza resultante de cualquier numero de fuerzas coplanares mediante la suma algebraica de las componentes x, y de todas las fuerzas
1.8 Equilibrio de una partícula: línea de acción, fuerzas concurrentes, diagrama de cuerpo libre y polígono cerrado.
Se dice que una partícula está en equilibrio si permanece en reposo y en un principio estaba en reposo, o si tiene una velocidad constante y originalmente estaba en movimiento. Sin embargo, más a menudo, el término “equilibrio” o, de manera más específica, “equilibrio estático” se usa para describir un objeto en reposo.
Ingenieria mecánica estática 12. Hibbeler
Equilibrio de una partícula 2D
Para mantener el equilibrio, es necesario satisfacer la primera ley del movimiento de Newton, la cual requiere que la fuerza resultante que actúa sobre una partícula sea igual a cero. Esta condición puede ser establecida matemáticamente como
Ingenieria mecánica estática 12. Hibbeler
Equilibrio de una partícula 2D (Sistemas de fuerzas coplanares)
Ingenieria mecánica estática 12. Hibbeler
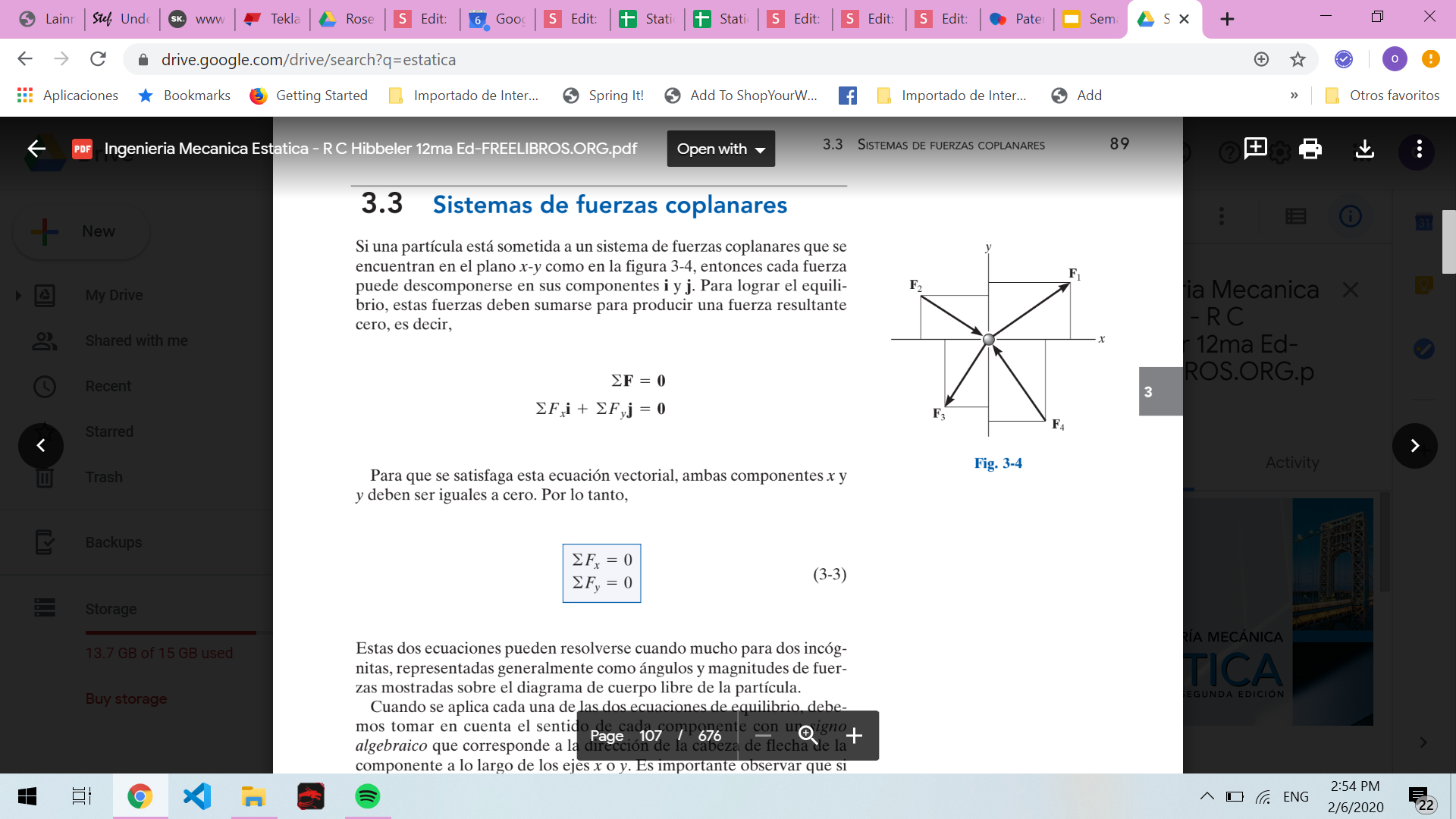
máximo 2 incognitas
Por lo que (en base a sus componentes):
Ejemplo
Ingenieria mecánica estática 12. Hibbeler

Ejercicio introductorio
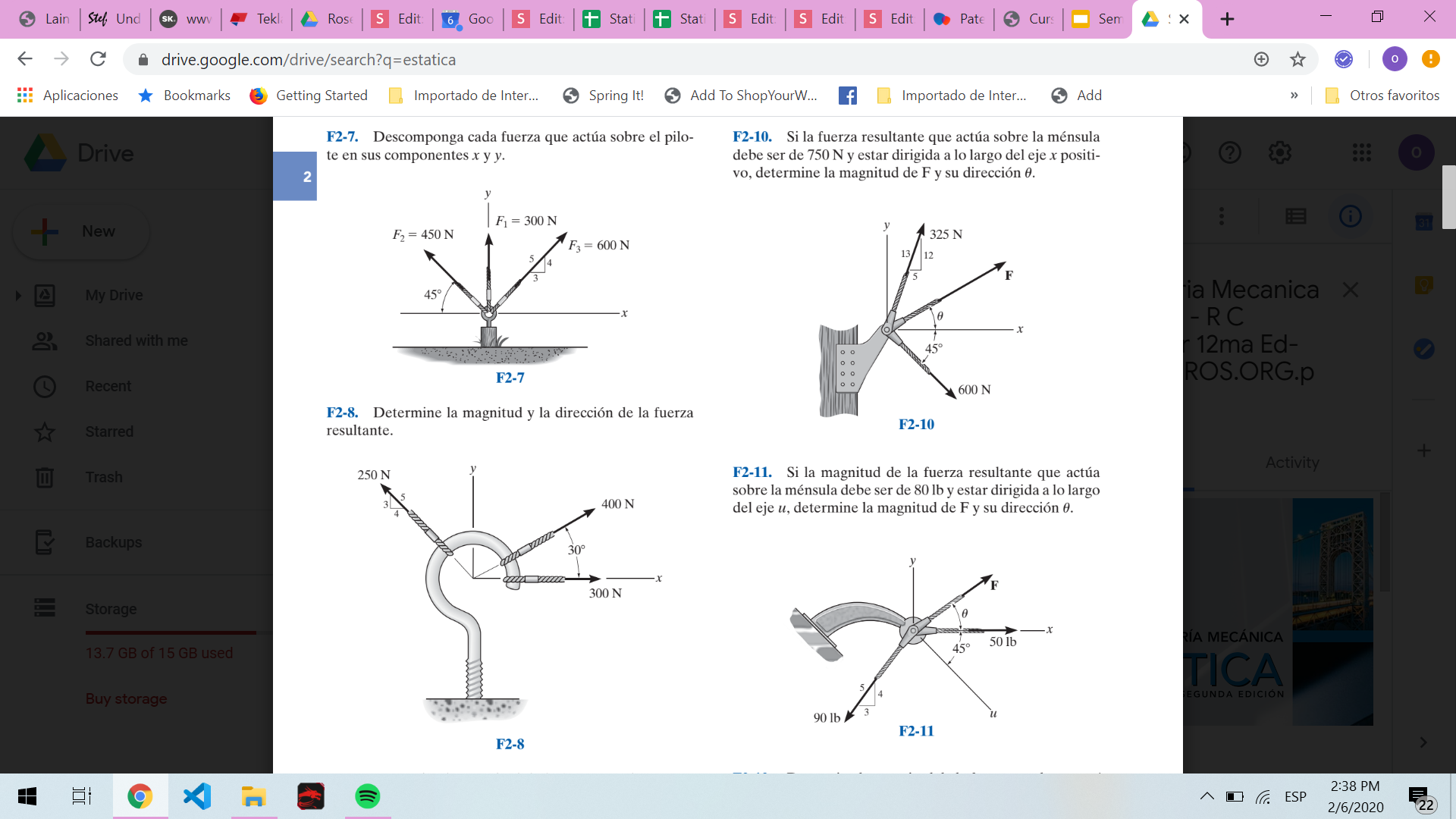
Ingenieria mecánica estática 12. Hibbeler
Procedimiento
Ingenieria mecánica estática 12. Hibbeler



Ejercicio introductorio

Ingenieria mecánica estática 12. Hibbeler
Ingenieria mecánica estática 12. Hibbeler

Equilibrio de una partícula 2D
Ejemplo
Ingenieria mecánica estática 12. Hibbeler

Ejemplo

Ingenieria mecánica estática 12. Hibbeler
Portafolio (Tarea)
Portafolio 4


2.23
Portafolio 4


Portafolio 4


2.2
2.8

2.3
Estática S5-2
By oscaralonso11
Estática S5-2
- 425



