Solving optimization problems using quantum computing in the NISQ era

Özlem Salehi

22.08.2022

Overview

Quantum annealing

TSPTW
Music generation
Music reduction
Test-vehicle optimization
Railway dispatching

QAOA

Error mitigation through mid-circuit measurement
FUNC-QAOA

Two main approaches

Quantum Annealing

Quantum Approximate Optimization Algorithm

Zhou, Leo, et al. "Quantum approximate optimization algorithm: Performance, mechanism, and implementation on near-term devices." Physical Review X 10.2 (2020): 021067.

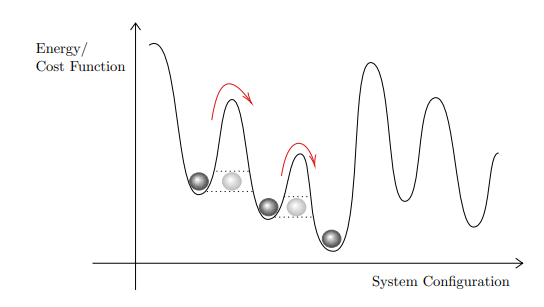
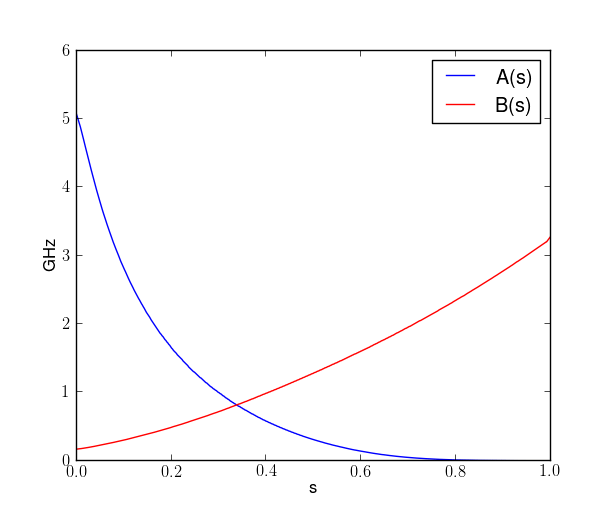
Quantum Annealing

Follows the adiabatic evolution defined through time-dependent Hamiltonian

Adiabatic Quantum Computing

$H(t) =(1-\frac{t}{\tau}) \:H_{\rm mix} + \frac{t}{\tau}\: H_c$

Slow evolution during time $\tau$

Quantum Adiabatic Theorem: A quantum system that starts in the ground state of a time-dependent Hamiltonian, remains in the in the instantaneous ground state provided the Hamiltonian changes sufficiently slowly.

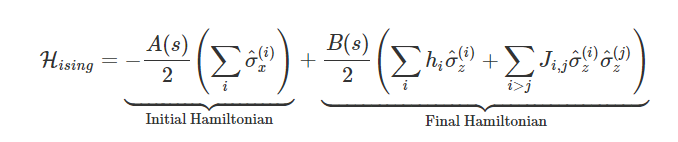
Quantum Annealing

Implemented by D-Wave quantum annealers

Some conditions of AQC are relaxed in QA resulting in a heuristic algorithm

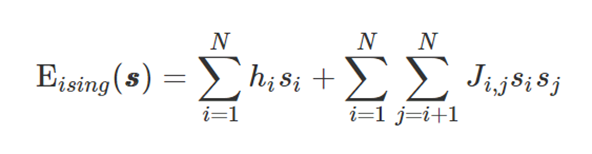
Express your problem as a
Quadratic
Unconstrained
Binary
Optimatization

problem

Solving a Problem Using QA

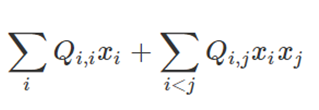
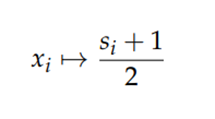
Obtain the equivalent Ising model

Use QA to find the variable assignment that minimizes energy

Considered Problems

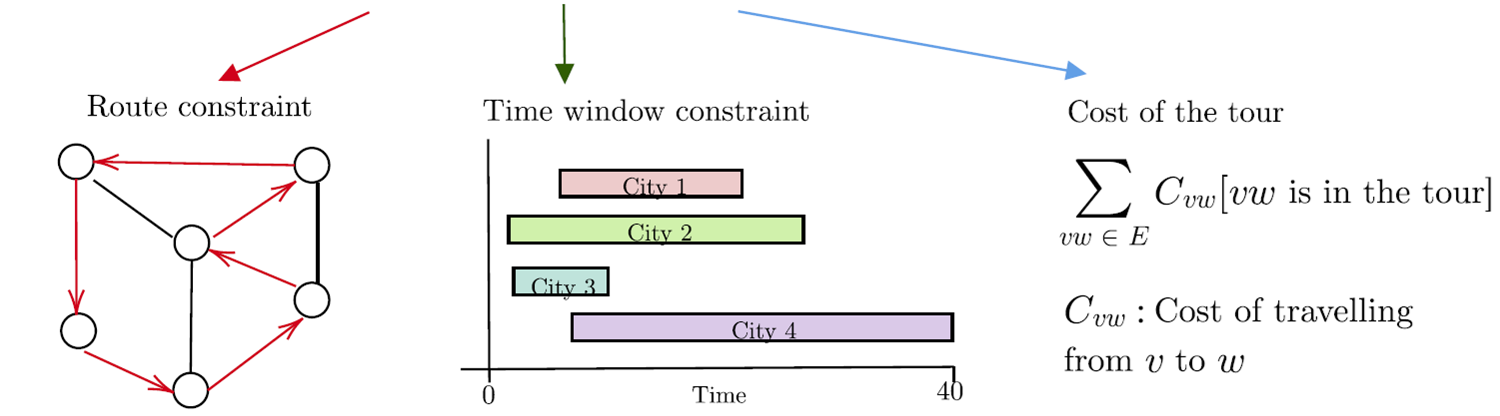
Travelling Salesman with Time Windows

Music generation

Music reduction

Test vehicle optimization

Railway dispatching problem

Travelling Salesman with Time Windows

Travelling Salesman Problem with Time Windows

Constraints

Objective

Salehi, Özlem, Adam Glos, and Jarosław Adam Miszczak. "Unconstrained binary models of the travelling salesman problem variants for quantum optimization." Quantum Information Processing 21.2 (2022): 1-30.

Aim: Find a closed route with minimum cost that visit each city exactly once obeying each city's time window.

QUBO for TSP

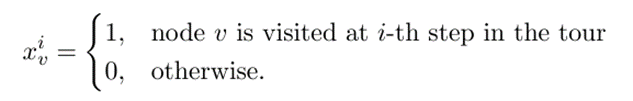
City 4

Step 2

Each city should be visited exactly once

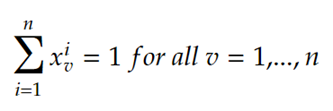
Only a single city should be visited at each time point

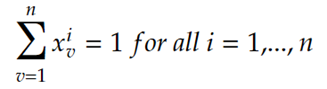
Objective

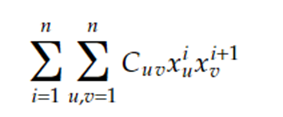
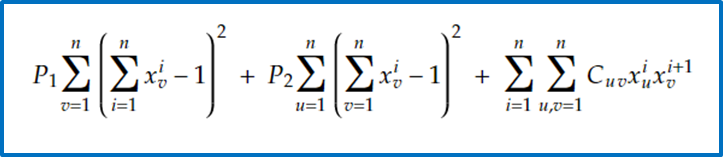
Penalty method

One-hot encoding

QUBO/HOBO for TSPTW

$O(n^3+n\delta)$ variables

$O(n^2+n\delta)$ variables
but not a QUBO

$O(n^2+n^2\delta)$ variables

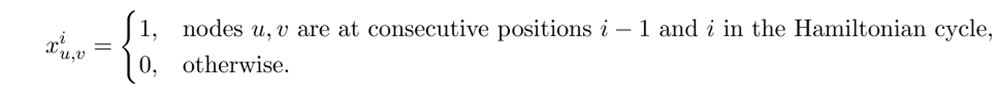
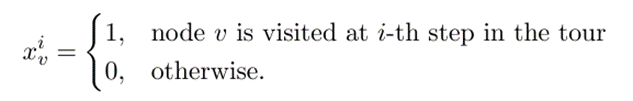
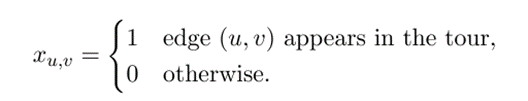
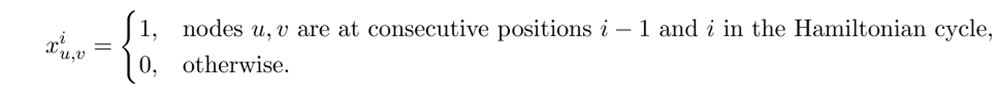
$x^1_{0,2}= 1$

$x^2_{2,5}= 1$

$x^3_{5,1}= 1$

$x^4_{1,3}= 1$

$x^5_{3,4}= 1$

$x^6_{4,0}= 1$

$i=1$

$i=2$

$i=3$

$i=4$

$i=5$

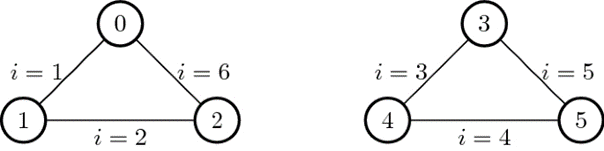
$i=6$

Undesired solution

$x^1_{0,2}=1$

$x^2_{2,5}=1$

$x^3_{5,1}=1$

$x^4_{1,3}=1$

$x^5_{3,4}=1$

$x^6_{4,0}=1$

Route Constraint

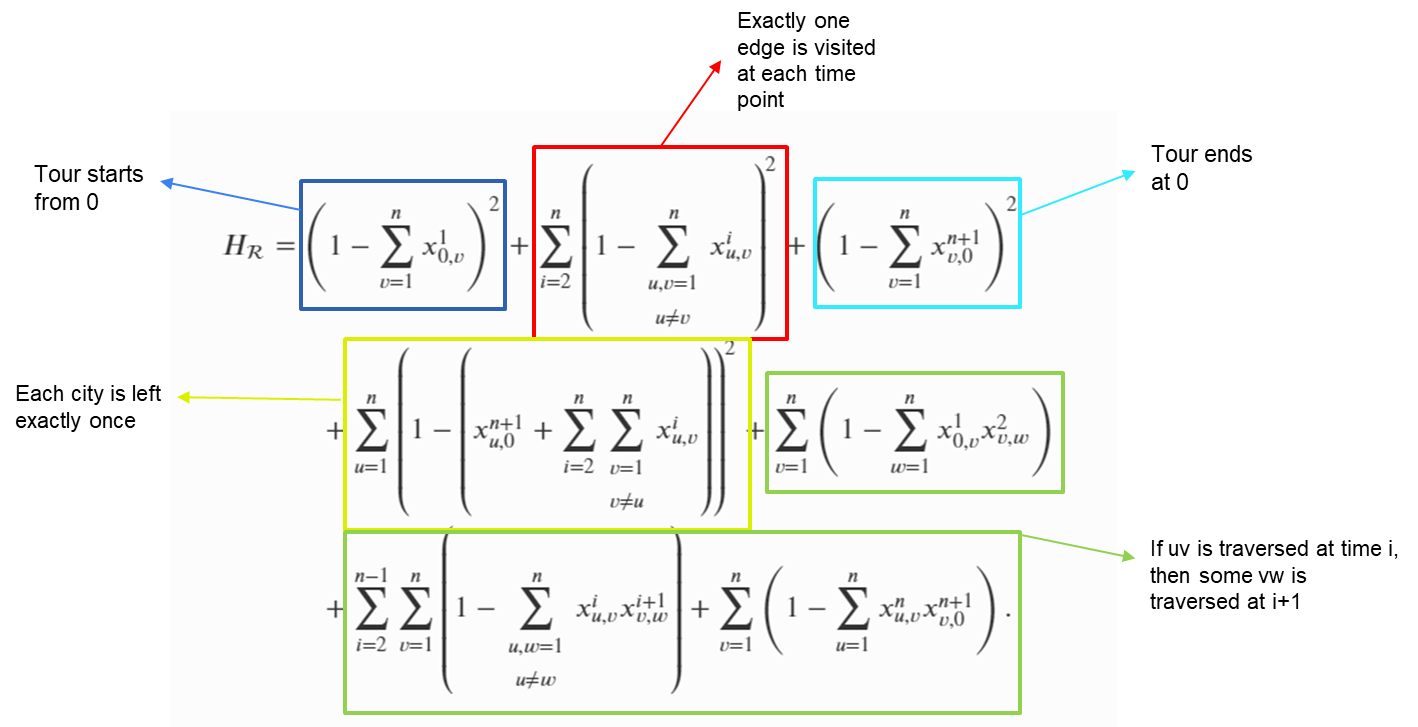
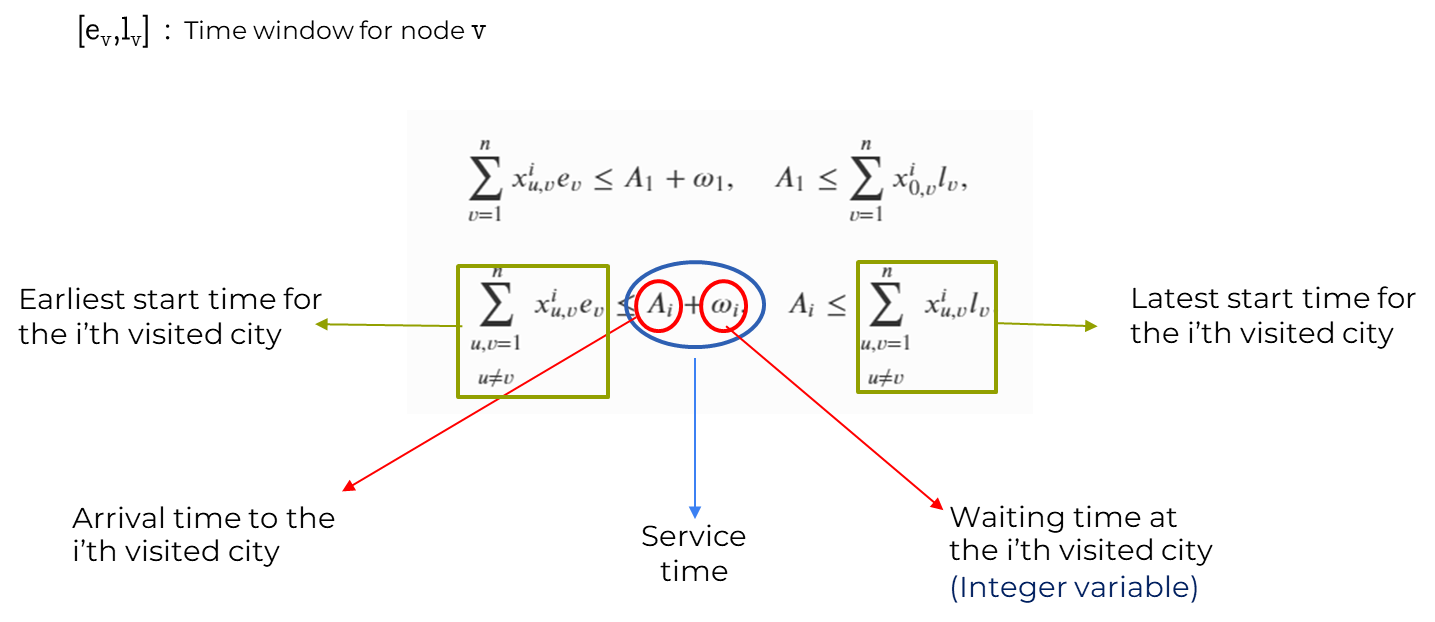
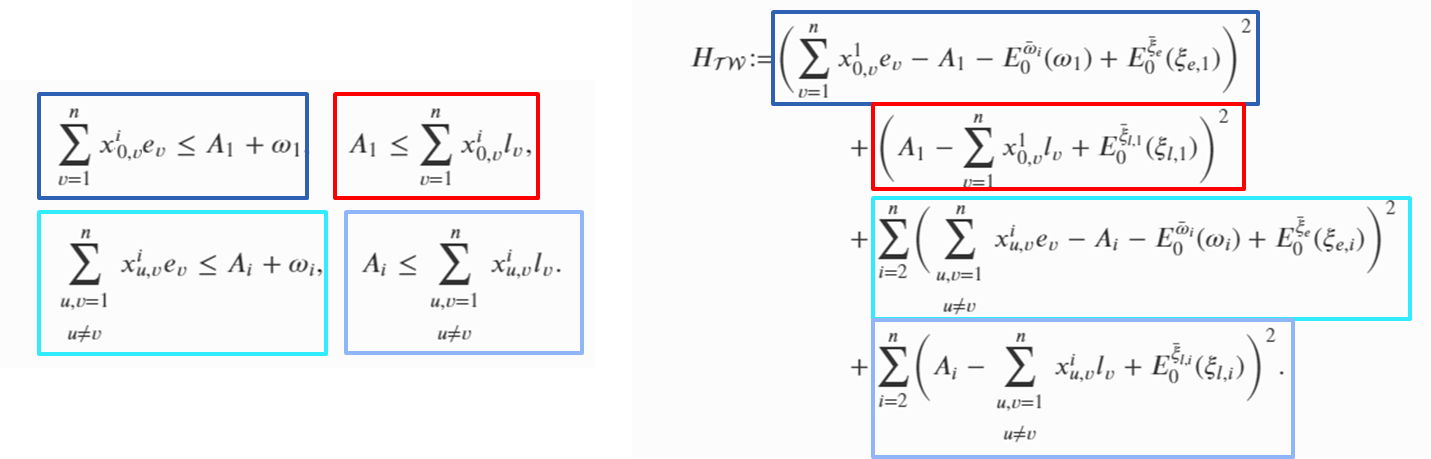
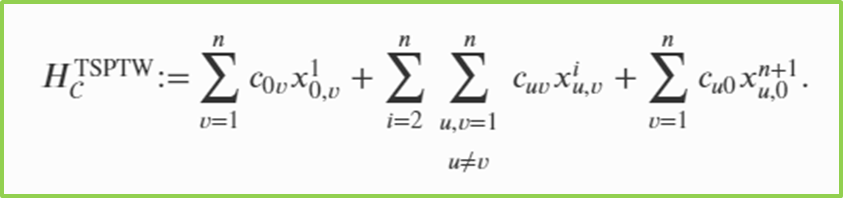
Time Window Constraint

Cost of the route

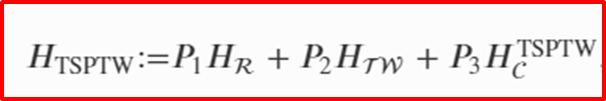
QUBO for TSPTW

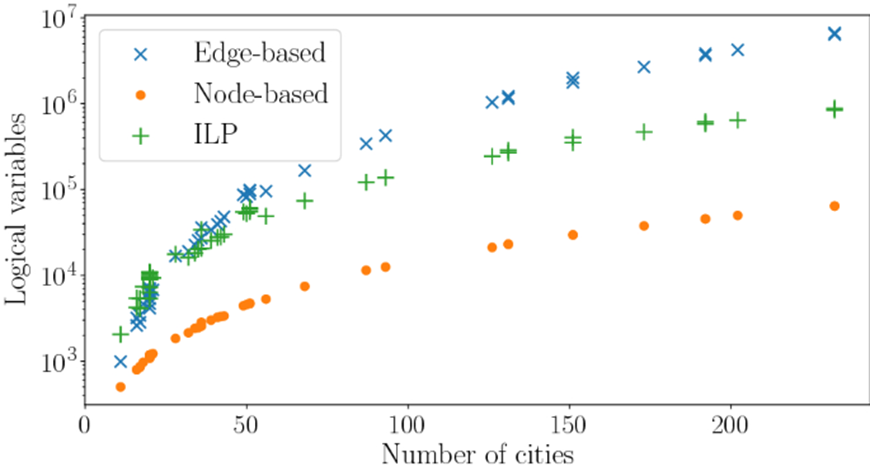
Comparison for number of variables

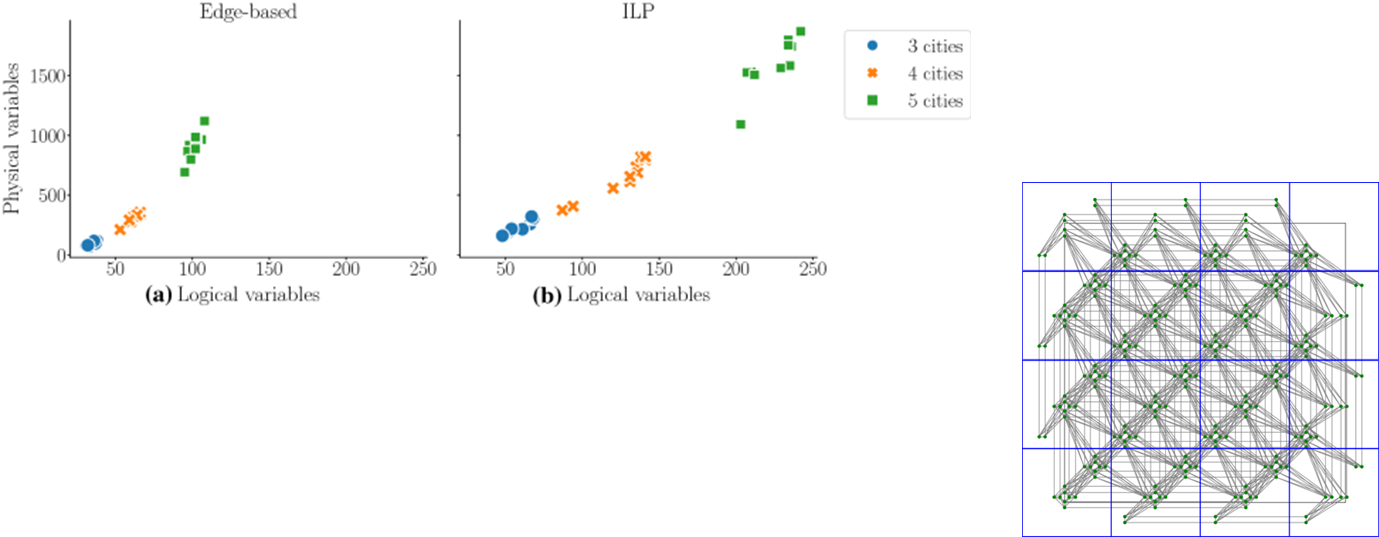
Embedding

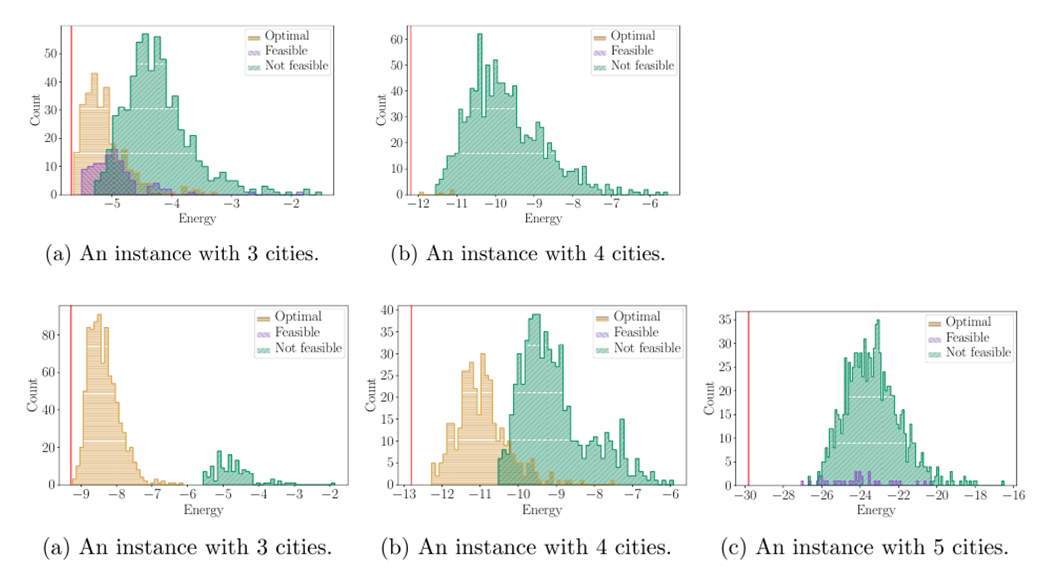
Experimental results

Multiple bit assignments correspond to the same solution
Choice of penalty values is challenging
Hybrid solvers by D-Wave can be a better alternative for large instances of TSPTW

Edge-based

ILP

Considered Problems

Travelling Salesman with Time Windows

Music generation

Music reduction

Test vehicle optimization

Railway dispatching problem

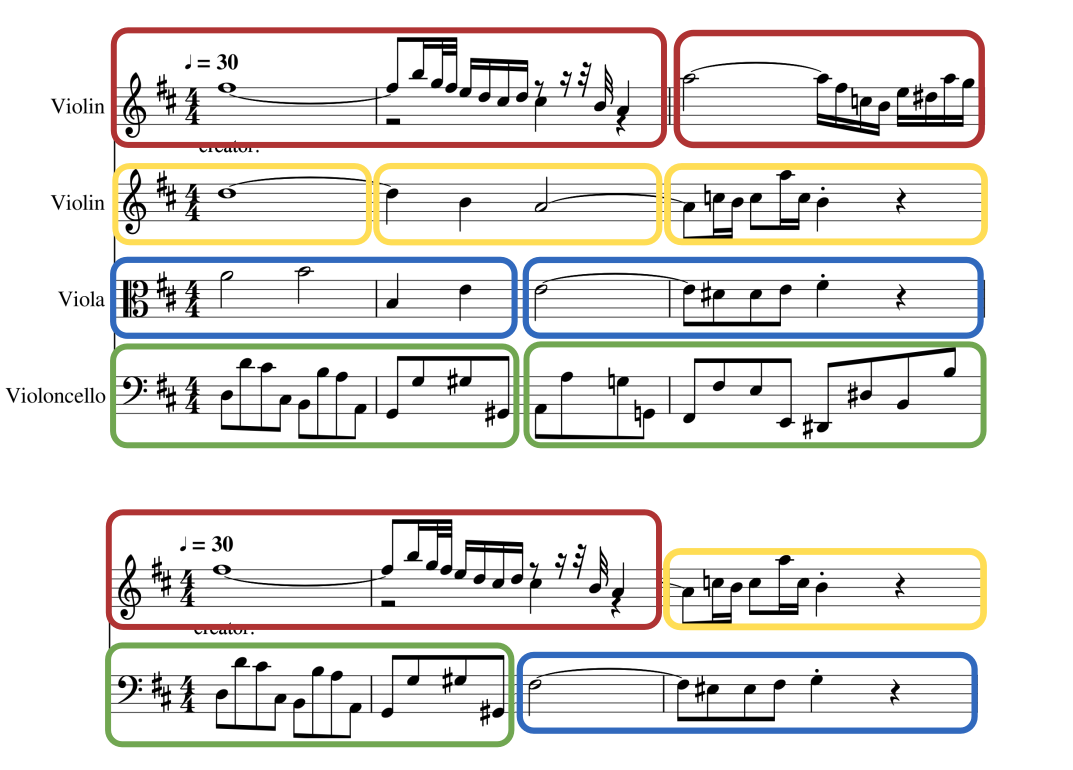
Music generation

Music Generation

Aim: Generate a melodic sequence of pitches

Pitches

that is plausible to the ear!

How to formulate this as an optimization process?

Arya, A., Botelho, L., Cañete, F., Kapadia, D., & Salehi, Ö. (2022). Music Composition Using Quantum Annealing. arXiv preprint arXiv:2201.10557.

Music Generation

x_{i,j} = \begin{cases}% 1 & \text{note at position $i$ is $j$,}\\ 0 & \text{otherwise.} \end{cases}

$$\sum_{j \in P} x_{i,j} = 1$$

$$\left ( 1- \sum_{j \in P} x_{i,j} \right )^2$$

Pitches

Rules about consecutive notes

$$x_{i,C} + x_{i+1,D} \leq 1$$

$$x_{i,C} + x_{i+1,C} + x_{i+2,C} \leq 2 $$

$$P=\{p_1,p_2,\dots,p_k \}$$

$x_{i,j}$ for $i \in [n]$ and $j \in P$

$$P=\{\mathtt{C}, \mathtt{D}, \mathtt{E}, \mathtt{G}\}$$

$$ -\sum_{ \substack{i\in [n-1] \\ j,j' \in P}} W_{j,j'} x_{i,j} x_{i+1,j'} $$

weights

Example: Ode to Joy excerpt

$$W_{F\#4,E4} = 2 $$

$$W_{F\#4,F\#4} = 2$$

$$W_{F\#4,G4} = 1$$

Objective

Music generated by hybrid solver

What else can be done?

Generate rhythm
Generate harmony
Use Markov Random Field to model the optimization problem

Considered Problems

Travelling Salesman with Time Windows

Music generation

Music reduction

Test vehicle optimization

Railway dispatching problem

Music reduction

Music Reduction

Aim: Given a music piece with T tracks, obtain a new music with M<T tracks keeping the characteristics of the song as much as possible

Phrase Identification

Cambouropoulos, Emilios. "The local boundary detection model (LBDM) and its application in the study of expressive timing." In ICMC, p. 8. 2001.

Phrase Selection

Phrase Identification

Phrase Selection

Which phrases to select?

Phrases with more information should be selected $\implies$ larger entropy

No two overlapping phrases should be selected for the same track

Operational fixed job scheduling

The gap between selected phrases in the same track should be minimized

Operational fixed job scheduling with minimal idle-time

Operational fixed job scheduling

job number

time

Operational fixed job scheduling

job number

time

job number

time

Operational fixed job scheduling

OFISP$_{\text{min-i}}$

Variables and objective function

$$x_{i} =\begin{cases}1,& \text{if the job $b_i$ is selected}\\ 0, & \text{otherwise.}\end{cases} $$

$$\text{minimize: } \ - \sum_{j=1}^{N} w_ix_i$$

Constraints

$$\sum_{i: ~ k\in[s_i,e_i]} x_i \leq M \qquad \text{for $k = 0, \dots, K$ } $$

$M$: Number of machines

$N$: Number of jobs

$K$: Total time in discrete time units

$s_i$: Start time of job $b_i$

$e_i$: End time of job $b_i$

$$\sum_{i: ~ k\in[s_i,e_i]} x_i = M \qquad \text{for $k = 0, \dots, K$ } $$

QUBO for OFISP$_{\text{min-i}}$

$$ P_1 \sum_{k=1}^K \left(\sum_{i: ~ k\in[s_i,e_i]} x_i - M\right)^2 + P_2 \sum_{k=1}^K \left(\sum_{i: ~ k\in[s_i,e_i]} x_i + E(\xi_k) - M\right)^2 + \sum_{i=1}^N w_ix_i , $$

Postprocessing

Sort selected jobs according to their ending times

Postprocessing

Use greedy algorithm to assign jobs to tracks

Considered Problems

Travelling Salesman with Time Windows

Music generation

Music reduction

Test vehicle optimization

Railway dispatching problem

Test vehicle optimization

Test-vehicle optimization

Glos, Adam, Akash Kundu, and Özlem Salehi. "Optimizing the Production of Test Vehicles using Hybrid Constrained Quantum Annealing." arXiv preprint arXiv:2203.15421 (2022).

Aim: Given a list of tests, requiring cars with certain features find the minimum number of cars that cover the tests and obey the configuration rules

Problem

Vehicle configuration rules

Single type requirement

Features allowed per type

Group Features

Rules per type

Test requirements

Properties of the cars needed for the testing phase

Algorithm

Select the features for $n$ cars to satisfy the tests as much as possible
Remove/update satisfied tests
Continue with the next $n$ cars

Greedy approach

D-Wave CQM Solver

P_i\in \mathbb{R}^{n\times n},\; q_i\in\mathbb{R}^n\;\textrm{and}\;r_i\in\mathbb{R}

\\ \\ \textrm{subject to}\; x^TP_ix+q_i^Tx\le r_i,\;\;\; i=1,...,m;\;\;\;x\ge0\\

\textrm{minimize}\; x^TP_0x+q_0^Tx\\

(1) CQM solver natively supports equality and inequality constraints.

(2) Less number of variables: As no need to remove inequality constraints through penalty method.

(3) Allows quadratic constraints directly into model, which is not possible for QUBO.

Constrained Quadratic Model

Advantages

P_i\in \mathbb{R}^{n\times n},\; q_i\in\mathbb{R}^n\;\textrm{and}\;r_i\in\mathbb{R}

(1) CQM solver natively supports equality and inequality constraints.

(2) Less number of variables: As no need to remove inequality constraints through penalty method.

(3) Allows quadratic constraints directly into model, which is not possible for QUBO.

Problem Formulation

Main challenge: Express the logical constraints as equality and inequality constraints using as few variables as possible

T_1:\; F_2\wedge\neg{F_4}\wedge\neg{F_5}\implies F_1\vee F_3

n\cdot f\; \textrm{binary variables}\; b_{i,j}

n\cdot o\; \textrm{binary variables}\; t_{i,j}

n\cdot q\; \textrm{binary variables}\; p_{i,j}

\textrm{overall}\; O(n(f + o + q))\; \textrm{binary variables}

n\rightarrow\textrm{number of test vehicles}\\ f\rightarrow\textrm{number of features}\\ o\rightarrow\textrm{different types available}\\ q\rightarrow\textrm{test requirements}\\

b_{i,j} = 1\;\textrm{iff}\;\textrm{vehicle}\;i\in[n]\;\textrm{has features}\;j\in[f]\\ t_{i,j} = 1\;\textrm{iff}\;\textrm{vehicle}\;i\in[n]\;\textrm{has type}\;j\in[o]\\ p_{i,j} = 1\;\textrm{iff}\;\textrm{vehicle}\;i\in[n]\;\textrm{used in test}\;j\in[q]\\

n\cdot f\; \textrm{binary variables}\; b_{i,j}

n\cdot o\; \textrm{binary variables}\; t_{i,j}

n\cdot q\; \textrm{binary variables}\; p_{i,j}

\textrm{overall}\; O(n(f + o + q))\; \textrm{binary variables}

T_1:\; F_2\wedge\neg{F_4}\wedge\neg{F_5}\implies F_1\vee F_3

n\rightarrow\textrm{number of test vehicles}\\ f\rightarrow\textrm{number of features}\\ o\rightarrow\textrm{different types available}\\ q\rightarrow\textrm{test requirements}\\

Numerical Results

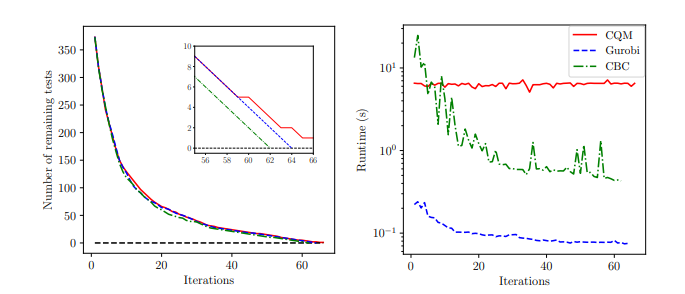
CBC: 62

Gurobi: 64

CQM: 66

$n=1$: One car optimized at a time

Considered Problems

Travelling Salesman with Time Windows

Music generation

Music reduction

Test vehicle optimization

Railway dispatching problem

Railway dispatching problem

Railway Dispatching Problem

Domino, Krzysztof, et al. "Quadratic and higher-order unconstrained binary optimization of railway dispatching problem for quantum computing." arXiv preprint arXiv:2107.03234 (2021).

Aim: Reduce delay propagation in railway systems in case of disruptions by rescheduling and rerouting

Objective: Minimize weighted additional delay

Constraints reflect minimal headway between trains, minimal stay on stations, station/track occupation, and rolling stock circulation on double-track and multi-track lines.

3 Formulations

ILP

HOBO

QUBO

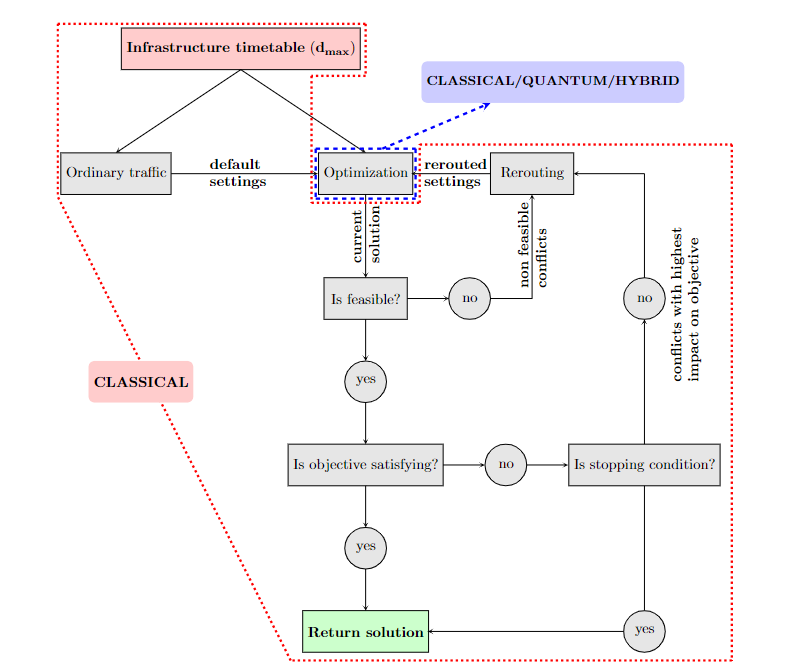
Algorithm

changing the track to the parallel one
changing the platform at the station
changing the path within the station

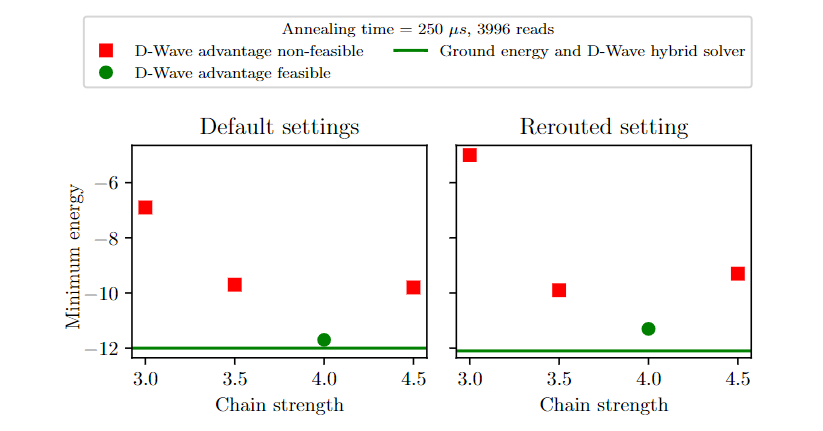
D-Wave Experiments

Two main approaches

Quantum Annealing

Quantum Approximate Optimization Algorithm

Zhou, Leo, et al. "Quantum approximate optimization algorithm: Performance, mechanism, and implementation on near-term devices." Physical Review X 10.2 (2020): 021067.

Quantum Approximate Optimization Algorithm

Quantum Approximate Optimization Algorithm (QAOA)

For the gate based model

$\gamma_i$ and $\beta_i$ optimized by external classical procedure

$$|\gamma,\beta\rangle = \prod_{i=1}^p \exp(-\mathrm{i} \beta_iH_{\rm mix})\exp(-\mathrm{i} \gamma_iH_c) |+^n\rangle $$

Can be viewed as a trotterization of AQC

Quantum Approximate Optimization Algorithm (QAOA)

$$|\gamma,\beta\rangle = \prod_{i=1}^p \exp(-\mathrm{i} \beta_iH_{\rm mix})\exp(-\mathrm{i} \gamma_iH_c) |+^n\rangle $$

Typical initial state

$-\sum_i X_i$ s.t. eigenstate of $X$ is $|+\rangle$

$2p$ parameters required for $p$ layers

Expectation $\langle \gamma,\beta| H_c | \gamma, \beta \rangle $ is approximated by measurement in the computational basis

Quantum Alternating Operator Ansatz (QAOA+)

$$|\gamma,\beta\rangle = \prod_{i=1}^p \exp(-\mathrm{i} \beta_iH_{\rm mix})\exp(-\mathrm{i} \gamma_iH_c) |s\rangle $$

Subspace of the full Hilbert space containig all feasible states

Should preserve the space

Example: One-hot states and XY Mixer

\frac{1}{\sqrt{3}} |001\rangle + |010\rangle +|100\rangle

\sum_{i=1} X_iX_{i+1} + Y_iY_{i+1}

Botelho, L., Glos, A., Kundu, A., Miszczak, J. A., Salehi, Ö., & Zimborás, Z. (2022). Error mitigation for variational quantum algorithms through mid-circuit measurements. Physical Review A, 105(2), 022441.

Error mitigation through mid-circuit measurement

Ideally, quantum state of the system should be a superposition of valid states throughout the evolution.

For TSP with ordinary encoding, product of one-hot states

Idea: Detect and remove unvalid states during the evolution

Postselection by filtering

If $|s\rangle$ is not a valid state, ancilla will no longer be in $|0\cdots0\rangle$ state

$\implies$ Measure ancilla and continue if it is all 0

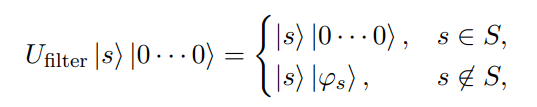
$k$-hot states: Count number of 1's
Domain wall encoding: Check consecutive bit pairs
Binary encoding: Check if encoded number exceeds maximum possible value

1000, 1100, 1110, 1111

Postselection by compression

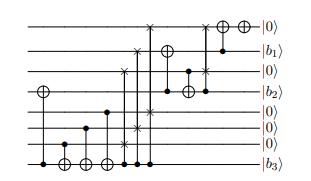
For one-hot states, apply the conversion circuit from one-hot to binary

Check if bits are 0

Experimental results

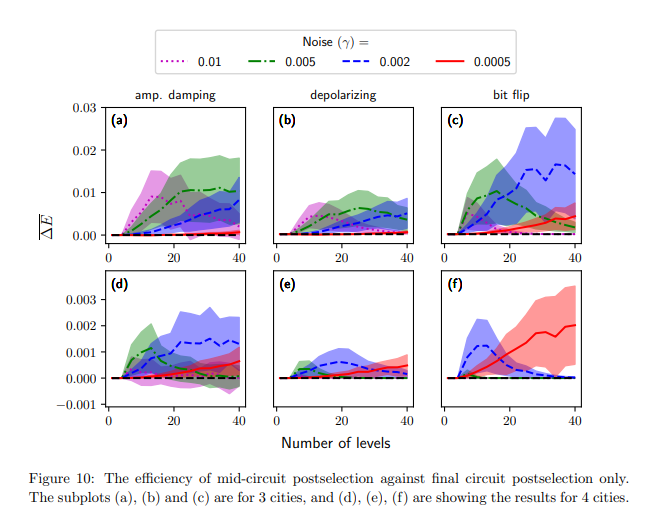
Larger the value, the more positive impact the mitigation scheme has on the output.

Near-Optimal Circuit Design for QAOA

We introduce an alternative way for implementing QAOA that allows reaching near-optimal cost metrics

Idea: Start with a classical pseudo-code function and implement it using a quantum circuit

State of the art

$b_i \leftarrow \frac{1-s_i}{2}$

Start with a
QUBO or HOBO

Get the corresponding Ising model

Implement each term in the expression

$H = -\frac{1}{2^n} \prod_{i=1}^n (1-s_i)$

$s_i \in \{-1,1\}$

$b_i \leftarrow \frac{1-s_i}{2}$

$H = -\prod_{i=1}^n b_i$

$b_i \in \{0,1\}$

Exponential number of CNOT gates!

Exponential number of terms !

$H = -\frac{1}{2^n} \prod_{i=1}^n (1-s_i)$

$s_i \in \{-1,1\}$

State of the art implementation

$O(n^2)$ gates on LNN!

FUNC-QAOA

This is classical AND operator!

$H = -\prod_{i=1}^n b_i$

$b_i \in \{0,1\}$

New Idea

Start with a pseudocode function!

$|f\rangle \leftarrow AND(b_i$ for $i=1$ to $n$)

$|f\rangle \leftarrow R_z(-i\theta) |f \rangle $

Uncompute $|f\rangle $

Number of gates
Number of physical qubits
Effective space size
Number of parameterized gates
Depth
Depth on LNN
Energy span

What else are important?

Quality Measures

Claim: FUNC-QAOA allows near-optimal circuit designs for various problems

FUNC-QAOA for TSP

Mixer: Grover-mixer
Initial state: Product of equal superposition of valid cities
Encoding: Binary

\frac{1}{\sqrt{3}} (|00\rangle + |01\rangle + |10\rangle)

Each $b_t$ (which represents in binary city visited at time $t$) is initialized as the equal superposition of valid cities

Permutation checking

Idea:

Count occurrence of each city in modulo 2
If they are not all 1, penalize

Cost of the route

Idea:

Switch from time-to-city to city-to city representation

The idea can be generalized, so far we managed to use it for

Set Cover problem
Integer Linear Problem (trade-off)
Graph Isomorphism (trade-off in general, optimal for Euclidean graphs)

Very difficult for general graph!

Generalization

References

Credits for presentation: Ludmila Botelho, Akash Kundu, Adam Glos

1. Salehi, Ö., Glos, A., & Miszczak, J. A. (2022). Unconstrained binary models of the travelling salesman problem variants for quantum optimization. Quantum Information Processing, 21(2), 1-30.

2. Arya, A., Botelho, L., Cañete, F., Kapadia, D., & Salehi, Ö. (2022). Music Composition Using Quantum Annealing. arXiv preprint arXiv:2201.10557.

3. Glos, A., Kundu, A., & Salehi, Ö. (2022). Optimizing the Production of Test Vehicles using Hybrid Constrained Quantum Annealing. arXiv preprint arXiv:2203.15421.

4. Domino, K., Kundu, A., Salehi, Ö., & Krawiec, K. (2021). Quadratic and higher-order unconstrained binary optimization of railway dispatching problem for quantum computing. arXiv preprint arXiv:2107.03234.

5. Botelho, L., Glos, A., Kundu, A., Miszczak, J. A., Salehi, Ö., & Zimborás, Z. (2022). Error mitigation for variational quantum algorithms through mid-circuit measurements. Physical Review A, 105(2), 022441.

Solving optimization problems using quantum computing in the NISQ era

By Özlem

Solving optimization problems using quantum computing in the NISQ era

Solving optimization problems using quantum computing in the NISQ era

Overview

Two main approaches

Quantum Annealing

Quantum Approximate Optimization Algorithm

Quantum Annealing

Adiabatic Quantum Computing

Quantum Annealing

Solving a Problem Using QA

Considered Problems

Travelling Salesman Problem with Time Windows

QUBO for TSP

City 4

Step 2

QUBO/HOBO for TSPTW

Route Constraint

Time Window Constraint

Time Window Constraint

Cost of the route

QUBO for TSPTW

Comparison for number of variables

Embedding

Experimental results

Considered Problems

Music Generation

Music Generation

Objective

Music generated by hybrid solver

What else can be done?

Considered Problems

Music Reduction

Phrase Identification

Phrase Selection

Phrase Selection

Phrase Selection

Phrase Selection

Phrase Selection

Which phrases to select?

Operational fixed job scheduling

Operational fixed job scheduling

Operational fixed job scheduling

OFISP\(_{\text{min-i}}\)

QUBO for OFISP\(_{\text{min-i}}\)

Postprocessing

Postprocessing

Postprocessing

Considered Problems

Test-vehicle optimization

Problem

Algorithm

D-Wave CQM Solver

Problem Formulation

Numerical Results

Considered Problems

Railway Dispatching Problem

3 Formulations

Algorithm

D-Wave Experiments

Two main approaches

Quantum Annealing

Quantum Approximate Optimization Algorithm

Quantum Approximate Optimization Algorithm

Quantum Approximate Optimization Algorithm (QAOA)

Quantum Approximate Optimization Algorithm (QAOA)

Quantum Alternating Operator Ansatz (QAOA+)

Error mitigation through mid-circuit measurement

Postselection by filtering

Postselection by compression

Experimental results

Near-Optimal Circuit Design for QAOA

State of the art implementation

New Idea

What else are important?

FUNC-QAOA for TSP

Permutation checking

Cost of the route

Generalization

References

Solving optimization problems using quantum computing in the NISQ era

More from Özlem