My Quantum Journey
Özlem Salehi
11.10.2022
Qiskit Quantum Explorers
Quantum Women Invited Talk Series
B.S. in Mathematics
Boğaziçi University, Turkey, 2011
M.S. in Computer Engineering
Boğaziçi University, Turkey, 2013
Ph.D. in Computer Engineering
Boğaziçi University, Turkey, 2019
Teaching assistant
Boğaziçi University, Turkey, 2011 - 2019
Instructor
Özyeğin University, Turkey, 2019 - 2021
Postdoctoral researcher
Institute of Theoretical and Applied Informatics Polish Academy of Sciences, Poland, 2021 -
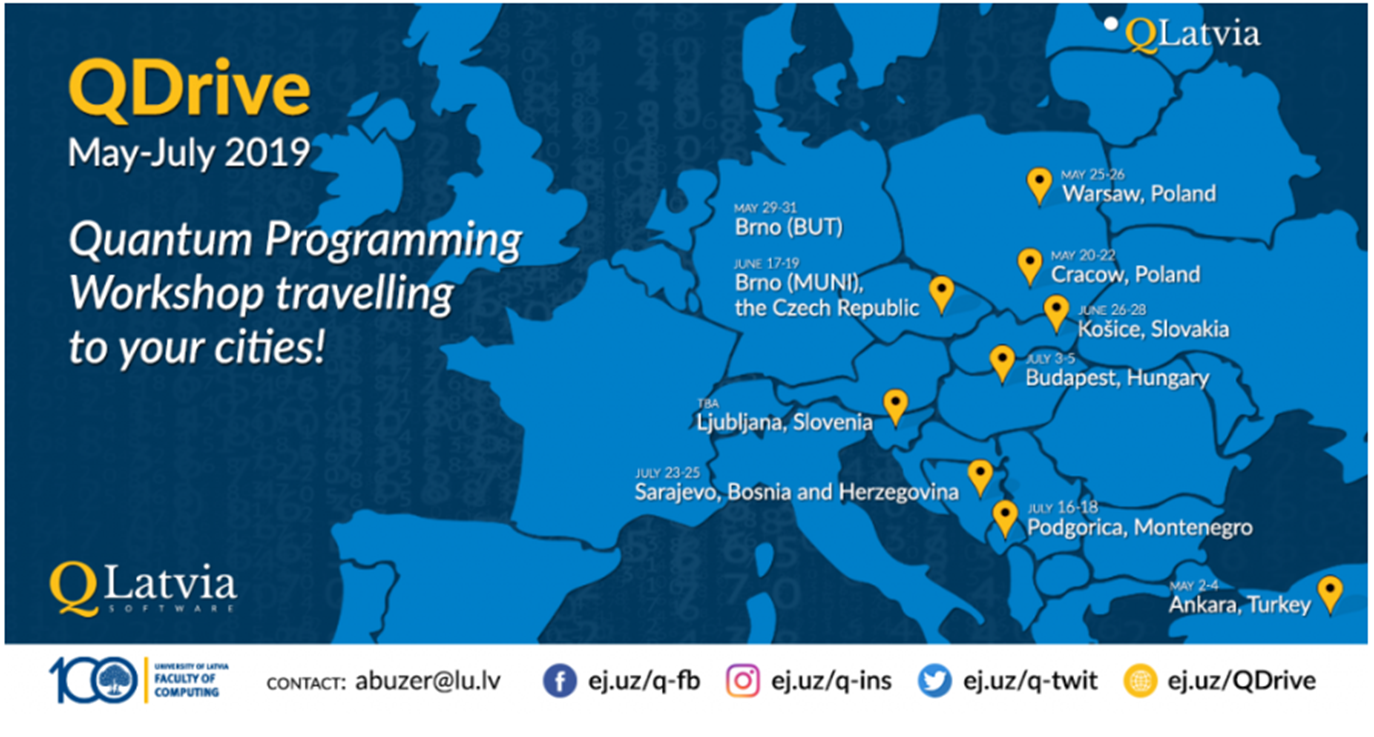
RESEARCH
Main Focus: Solving optimization problems using quantum computing in the NISQ era
Two main approaches
Quantum Annealing
Quantum Approximate Optimization Algorithm
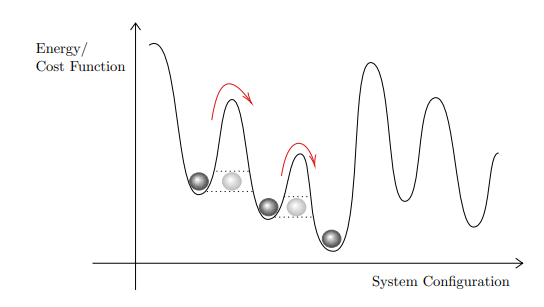
Zhou, Leo, et al. "Quantum approximate optimization algorithm: Performance, mechanism, and implementation on near-term devices." Physical Review X 10.2 (2020): 021067.
Quantum Annealing
Follows the adiabatic evolution defined through time-dependent Hamiltonian
Adiabatic Quantum Computing
\(H(t) =\frac{1-t}{\tau} \:H_{\rm mix} + \frac{t}{\tau}\: H_c\)
Slow evolution during time \(\tau\)
Quantum Adiabatic Theorem: A quantum system that starts in the ground state of a time-dependent Hamiltonian, remains in the in the instantaneous ground state provided the Hamiltonian changes sufficiently slowly.
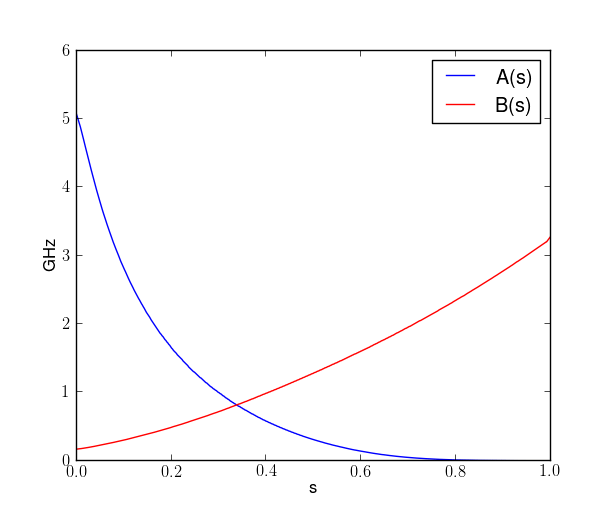
Quantum Annealing
Implemented by D-Wave quantum annealers
Some conditions of AQC are relaxed in QA resulting in a heuristic algorithm
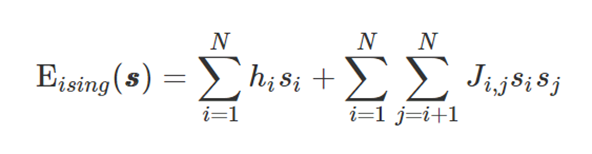
Quadratic Uncostrained Binary Optimization (QUBO)
\min.~f(x_1,x_2) = 5x_1 + 9x_2 -6x_1x_2
- \(x_1 = 0\) and \(x_2 = 0\): \(f(0,0) = 5\cdot 0 + 9\cdot 0 - 6\cdot 0\cdot 0 = 0\)
- \(x_1 = 0\) and \(x_2 = 1\): \(f(0,1) = 5\cdot 0 + 9\cdot 1 - 6\cdot 0\cdot 1 = 9\)
- \(x_1 = 1\) and \(x_2 = 0\): \(f(1,0) = 5\cdot 1 + 9\cdot 0 - 6\cdot 1\cdot 0 = 5\)
- \(x_1 = 1\) and \(x_2 = 1\): \(f(1,1) = 5\cdot 1 + 9\cdot 1 - 6\cdot 1\cdot 1 = 8\)
\(\displaystyle \min.~\sum_{i} Q_{i,i} x_i + \sum_{i<j} Q_{i,j}x_i x_j \)
Constrained problem:
\(\min.~~ f(x_1,x_2)\)
\(s.t.~~~~x_1+x_2\geq 1\)
QUBO for TSP
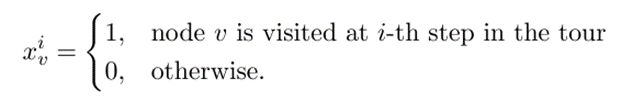
1, node \(i\) is visited at step \(t\) in the tour
0, otherwise
\(\displaystyle \sum_{i=0}^{n-1} b_{t,i}=1\) for all \(t=0,\dots,n-1\)
City \(i\) is visited
exactly once
\(\displaystyle \sum_{t=0}^{n-1} b_{t,i}=1\) for all \(i=0,\dots,n-1\)
At time \(t\) exactly one city is visited
Constraints
Objective
If both variables are 1, this means \(ij\) is traversed at time \(t\)
\(b_{t,i}\)
\(\displaystyle \sum_{\substack{i,j=0 \\ i\neq j }}^{n-1} W_{ij} \)
\(\displaystyle \sum_{t=0}^{n-1}b_{t,i}b_{t+1,j}\)
Express your problem as a
Quadratic
Unconstrained
Binary
Optimatization
problem
Solving a Problem Using QA
Obtain the equivalent Ising model
Use QA to find the variable assignment that minimizes energy
\(\displaystyle \sum_{i} Q_{i,i} x_i + \sum_{i<j} Q_{i,j}x_i x_j \)
\(x_i \mapsto \frac{s_i+1}{2}\)
\(\displaystyle \sum_{i} h_i s_i + \sum_{i<j} J_{i,j}s_i s_j \)
Quantum annealing - Pros and Cons
- Embedding problem
- Noise - error correction?
DISADVANTAGES
- Larger number of qubits
- Aims at optimization problems - real-world applications
ADVANTAGES
Considered Problems
Travelling Salesman with Time Windows
Music generation
Music reduction
Test vehicle optimization
Railway dispatching problem
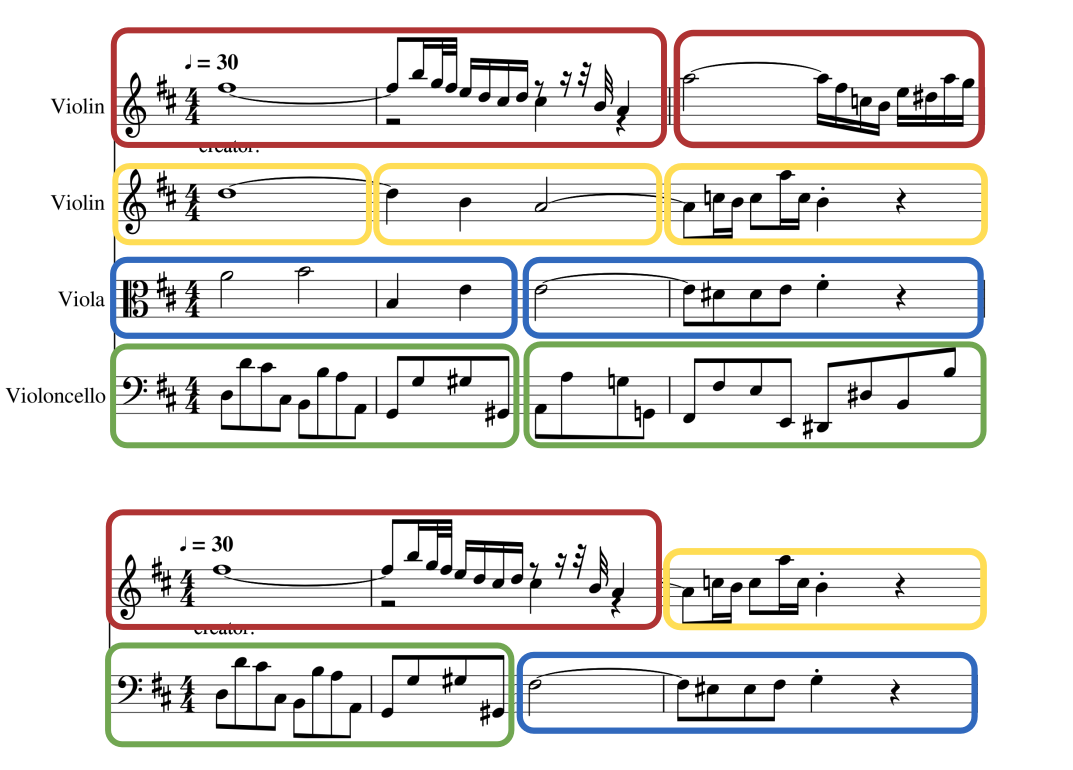
Travelling Salesman Problem with Time Windows
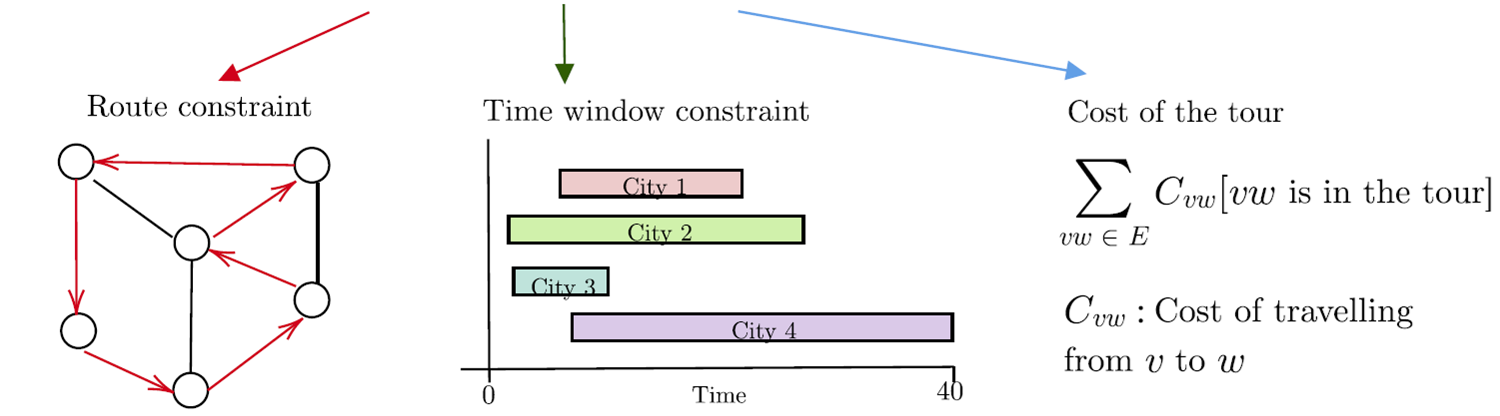
Constraints
Objective
Salehi, Ö., Glos, A. and Miszczak, J.A., 2022. Unconstrained binary models of the travelling salesman problem variants for quantum optimization. Quantum Information Processing, 21(2), pp.1-30.
Aim: Find a closed route with minimum cost that visit each city exactly once obeying each city's time window.
Music Generation
Aim: Generate a melodic sequence of pitches
Pitches
that is plausible to the ear!
How to formulate this as an optimization process?
Arya, A., Botelho, L., Cañete, F., Kapadia, D., & Salehi, Ö. (2022). Music Composition Using Quantum Annealing. to appear in Quantum Computer Music: Foundations, Methods and Advanced Concepts : Springer, 2022.
Music Reduction
Aim: Given a music piece with T tracks, obtain a new music with M<T tracks keeping the characteristics of the song as much as possible
Test-vehicle optimization
Glos, A., Kundu, A. and Salehi, Ö., 2022. Optimizing the Production of Test Vehicles using Hybrid Constrained Quantum Annealing. arXiv preprint arXiv:2203.15421.
Aim: Given a list of tests, requiring cars with certain features, find the minimum number of cars that cover the tests and obey the configuration rules
Railway Dispatching Problem
Domino, K., Kundu, A., Salehi, Ö. and Krawiec, K., 2022. Quadratic and higher-order unconstrained binary optimization of railway rescheduling for quantum computing. Quantum Information Processing, 21(9), pp.1-33.
Aim: Reduce delay propagation in railway systems in case of disruptions by rescheduling and rerouting
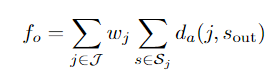
Objective: Minimize weighted additional delay
Constraints reflect minimal headway between trains, minimal stay on stations, station/track occupation, and rolling stock circulation on double-track and multi-track lines.
Two main approaches
Quantum Annealing
Quantum Approximate Optimization Algorithm
Zhou, Leo, et al. "Quantum approximate optimization algorithm: Performance, mechanism, and implementation on near-term devices." Physical Review X 10.2 (2020): 021067.
Quantum Approximate Optimization Algorithm
Quantum Approximate Optimization Algorithm (QAOA)
For the gate based model
\(\gamma_i\) and \(\beta_i\) optimized by external classical procedure
$$|\gamma,\beta\rangle = \prod_{i=1}^p \exp(-\mathrm{i} \beta_iH_{\rm mix})\exp(-\mathrm{i} \gamma_iH_c) |+^n\rangle $$
Can be viewed as a trotterization of AQC
Quantum Approximate Optimization Algorithm (QAOA)
$$|\gamma,\beta\rangle = \prod_{i=1}^p \exp(-\mathrm{i} \beta_iH_{\rm mix})\exp(-\mathrm{i} \gamma_iH_c) |+^n\rangle $$
Typical initial state
\(-\sum_i X_i\) s.t. eigenstate of \(X\) is \(|+\rangle\)
\(2p\) parameters required for \(p\) layers
Expectation \(\langle \gamma,\beta| H_c | \gamma, \beta \rangle \) is approximated by measurement in the computational basis
Quantum Alternating Operator Ansatz (QAOA+)
$$|\gamma,\beta\rangle = \prod_{i=1}^p \exp(-\mathrm{i} \beta_iH_{\rm mix})\exp(-\mathrm{i} \gamma_iH_c) |s\rangle $$
Subspace of the full Hilbert space containing all feasible states
Should preserve the space
Example: One-hot states and XY Mixer
1/\sqrt{3} ~ ( |100\rangle + |010\rangle +|001\rangle)
\sum_{i=1} X_iX_{i+1} + Y_iY_{i+1}
\(b_{0,0}\)
\(b_{0,1}\)
\(b_{0,2}\)
\(b_{1,0}\)
\(b_{1,1}\)
\(b_{1,2}\)
\(b_{2,0}\)
\(b_{2,1}\)
\(b_{2,2}\)
\(t=0\)
\(t=1\)
\(t=2\)
1/\sqrt{8} ~ ( |000\rangle + |001\rangle + \dots + |111\rangle)
1/\sqrt{8} ~ ( |000\rangle + |001\rangle + \dots + |111\rangle)
1/\sqrt{8} ~ ( |000\rangle + |001\rangle + \dots + |111\rangle)
1/\sqrt{3} ~ ( |100\rangle + |010\rangle +|001\rangle)
1/\sqrt{3} ~ ( |100\rangle + |010\rangle +|001\rangle)
1/\sqrt{3} ~ ( |100\rangle + |010\rangle +|001\rangle)
Botelho, L., Glos, A., Kundu, A., Miszczak, J. A., Salehi, Ö., & Zimborás, Z. (2022). Error mitigation for variational quantum algorithms through mid-circuit measurements. Physical Review A, 105(2), 022441.
Error mitigation through mid-circuit measurement
Ideally, quantum state of the system should be a superposition of valid states throughout the evolution.
For TSP with one-hot encoding, product of one-hot states
Idea: Detect and remove unvalid states during the evolution
Postselection by filtering
If \(|s\rangle\) is not a valid state, ancilla will no longer be in \(|0\cdots0\rangle\) state
\(\implies\) Measure ancilla and continue if it is all 0
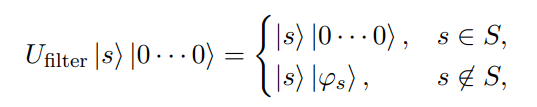
- \(k\)-hot states: Count number of 1's
- Domain wall encoding: Check consecutive bit pairs
- Binary encoding: Check if encoded number exceeds maximum possible value
1000, 1100, 1110, 1111
1000, 0100, 0010, 0001
00, 01, 10, 11
Postselection by compression
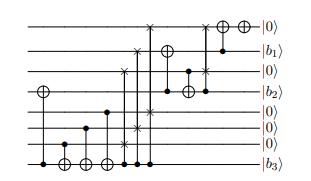
For one-hot states, apply the conversion circuit from one-hot to binary
Check if bits are 0
Near-Optimal Circuit Design for QAOA
We introduce an alternative way for implementing QAOA that allows reaching near-optimal cost metrics
Idea: Start with a classical pseudo-code function and implement it using a quantum circuit
State of the art
\(b_i \leftarrow \frac{1-s_i}{2}\)
Start with a
QUBO or HOBO
Get the corresponding Ising model
Implement each term in the expression
How to implement QAOA?
QUBO: \(\min.~\displaystyle \frac{1}{2}\sum_{(i,j) \in E}2x_ix_j - x_i - x_j \)
Ising model: \(\min.~ \displaystyle \frac{1}{2}\sum_{(i,j) \in E} (s_is_j-1)\)
\(\implies \min. \displaystyle \sum_{(i,j) \in E} s_is_j \)
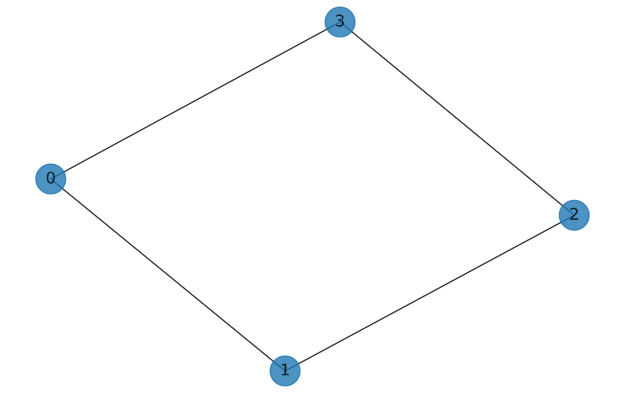
\(\displaystyle \sum_{(i,j) \in E} Z_iZ_j \)
Corresponding Hamiltonian:
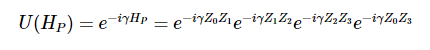
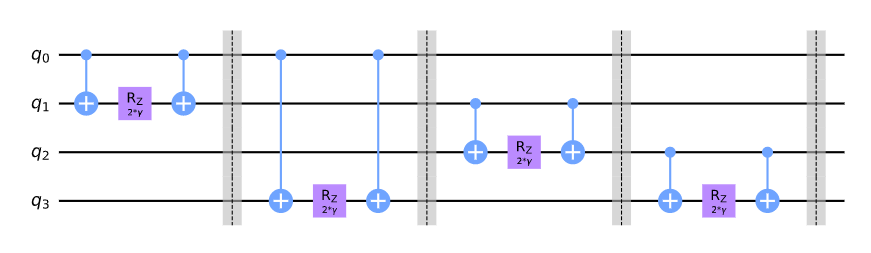
\(x_i \leftarrow \frac{1-s_i}{2}\)
https://qiskit.org/textbook/ch-applications/qaoa.html
\(b_i \leftarrow \frac{1-s_i}{2}\)
\(H = -\prod_{i=1}^n b_i\)
\(b_i \in \{0,1\}\)
Exponential number of CNOT gates!
Exponential number of terms !
\(H = -\frac{1}{2^n} \prod_{i=1}^n (1-s_i)\)
\(s_i \in \{-1,1\}\)
State of the art implementation
\(O(n^2)\) gates on LNN!
\(H = -\frac{1}{2^n} \prod_{i=1}^n (1-s_i)\)
\(s_i \in \{-1,1\}\)
Yet, there exists another efficient circuit
Claim: FUNC-QAOA allows near-optimal circuit designs for various problems
New Idea: Start with a classical pseudocode function
FUNC-QAOA
FUNC-QAOA for TSP
Mixer: Grover-mixer
Initial state: Product of equal superposition of valid cities
Encoding: Binary
\frac{1}{\sqrt{3}} (|00\rangle + |01\rangle + |10\rangle)
Each \(b_t\) (which represents in binary city visited at time \(t\)) is initialized as the equal superposition of valid cities
Permutation checking
Idea:
Count occurrence of each city in modulo 2
If they are not all 1, penalize
Cost of the route
Idea:
Switch from time-to-city to city-to-city representation
QUESTIONS
qiskit_talk
By Özlem
