Asymptotic behavior of Brownian motion maximum log-likelihood means
Pernille E.H. Hansen
University of Copenhagen
Content of talk
- Mean values on shape spaces
- The BM-maximum likelihood mean
- Law of Large Numbers
- Central Limit Theorem
- Example
Statistics on shape spaces
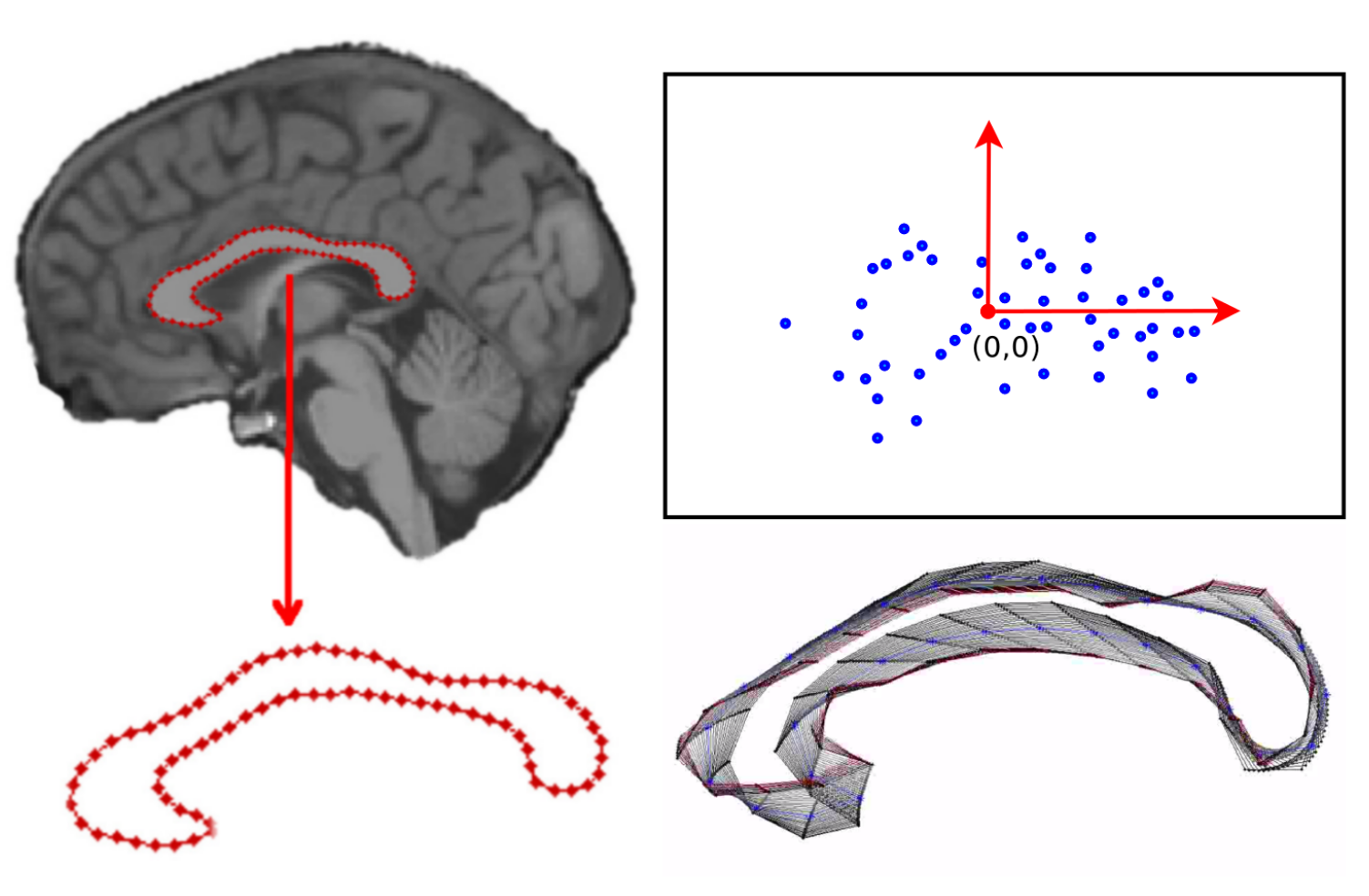
Medical Images
The sphere
\mathcal{S}^2
Manifolds
Mean value?
Y_1,...,Y_N\overset{\text{idd}}{\sim} Y \in
\mu = \mathbb{E}[Y]
Expected value:
Sample estimator:
\mu_N=\frac1N\sum_{i=1}^NY_i
Uniqueness, LLN, CLT
X_1,...,X_N\overset{\text{idd}}{\sim} X \in
\mathbb{R}^n
M
\mathbb{E}[X]
Fréchet mean
X:\Omega \to M
M = \arg\min_{y\in\mathcal{M}} \mathbb{E}[\text{dist}(y,X)^2]
The Riemann center of mass of a random variable is
If then is the Fréchet mean of
M = \{\mu \}
\mu
X.
For , the sample Fréchet function
X_1,...,X_N\overset{\text{iid}}{\sim} X
F_N(y) = \frac{1}{N}\sum_{i=1}^{N} \text{dist}(y,X_i)^2
M_N = \arg\min_{y\in M}F_N(y)
and sample Fréchet means
Estimation
Uniqueness, LLN, CLT
Limitation:
\text{dist}:M\times M \to \R
is not smooth on all of
M
Brownian motion maximum log-likelihood means
Heat kernel on manifolds
p:M \times M \times \mathbb{R}_+ \to \mathbb{R}_+
is called a heat kernel on if
(\partial_t-\Delta_x)p(x,y,t) = 0
\lim_{t\to 0} p(x,y,t)= \delta_x(y)
- M compact: Unique solution
- Else: Unique minimal solution
t = 0.1
t = 0.5
t = 1
smooth manifold
M
A map
p \in \mathcal{C}^\infty
M
Brownian motion on manifolds
A Brownian motion on is a Markov process with transition density function
p(x,y,t) \approx
\text{"probability" of hitting }y
\text{ in time }t\text{ when starting in }x
p(x,y,t)
(B_t)
M
x
B_t = y
Brownian motion on manifolds
A Brownian motion on is a Markov process with transition density function
p(x,y,t) \approx
\text{"probability" of hitting }y
\text{ in time }t\text{ when starting in }x
p(x,y,t)
(B_t)
M
X_1,...,X_n \overset{\text{iid}}{\sim}X\in M
Given
\mu = -\arg\min \mathbb{E}_X[\ln p(x,X,t)]
mean point of
X
\mu = \arg\max \frac{1}{n} \sum_{i=1}^n \ln(p(x,X_i,t))
most likely origin points of
(B_t)
Brownian motion maximum log-likelihood mean
X:\Omega \to \mathcal{M}
E_t = \arg\min_{y\in\mathcal{M}} \mathbb{E}[-\text{ln }p(X,y,t)]
For , the (BMML)-likelihood means of a random variable
are the minimizers of the likelihood function
t>0
E_t
L_t(y) = \mathbb{E}[-\text{ln }p(X,y,t)]
\lim_{t\to 0} -t\ln p (x,y,t) = \frac{\text{dist}(x,y)^2}{2}
Estimation
L_{t,n}(x) = -\frac{1}{N}\sum_{i=1}^N\ln p(x,X_i,t)
E_{t,n} = \arg\min_{x\in M} L_{t,n}(x)
For the sample likelihood function is
X_1,...,X_n \overset{\text{idd}}{\sim} X
with sample likelihood means
Can we say something about:
- (LLN)
- (CLT)
\mu_n \overset{\mathbb{P}}{\to} \mu
\sqrt{n}(\mu_n-\mu)\overset{\mathcal{D}}{\to} D
\mu_{t,n}\in E_{t,n}
measurable selection.
Fix
t>0.
Law of large numbers
Fix
t>0.
- (ZC) of Ziezold if
(E_{t,n})
\cap_{n=1}^\infty \overline{\cup_{k=n}^\infty E_{t,k}} \subset E_t \quad a.s.
- (BPC) Bhattacharya and Patrangenaru if
\forall \epsilon>0 \exist n\in \mathbb{N}:
\cup_{k=n}^\infty E_{t,k} \subset B(E_t,\epsilon) \quad a.s.
\mu
\mu_n
\mu_{n-1}
We say that is a SCE in the sense of
Law of large numbers
Fix
t>0, \enspace M
\mu
\mu_n
\mu_{n-1}
- satisfies (ZC) if either
- has compact support
- for all
-
satisfies (BPC) if
- satisfies (ZC)
- Heine-Borel property of
- (A coercivity condition)
Riemannian manifold,
X: \Omega \to M
\mathbb{E}[-\ln p (x,X,t)]<\infty
X
x\in M
(E_{t,n})
\overline{\cup_{n=1}^\infty E_{t,n}}
E_t \neq \emptyset
(E_{t,n})
(E_{t,n})
*(Huckemann, 2010)
compact Riemannian manifold
M
- satisfies (ZC)
- satisfies (BPC) if
E_t \neq \emptyset
(E_{t,n})
(E_{t,n})
Central Limit Theorem
and Smeariness
Central limit theorem & smeariness
\sqrt{n}\mu_n \overset{\mathcal{D}}{\to} \mathcal{N}(\mu,\Sigma)
X_1,...,X_n \overset{\text{idd}}{\sim} X
on with
\mathbb{R}^m
smeary:
k-
n^{\frac{1}{2(k+1)}}X_n \overset{\mathcal{D}}{\to} \mathscr{L}
Note: CLT 0-smeary
\Rightarrow
\mathbb{E}[X] = \mu,
\mu_n = \frac{1}{n}\sum_{i=1}^n X_i
CLT:
(X_n)\in \mathbb{R}^m
Central limit theorem & smeariness
(Y_n)
M
smeary
k-
n^{\frac{1}{2(k+1)}}X_n \overset{\mathcal{D}}{\to} \mathscr{L}
on Riemannian manifold
Define
X_n = \phi(Y_n)-\phi(\mu)\in \R^m
Does it there exist st is ?
(\mu_{t,n})
k\geq 0
(Y_n)
k-
smeary
\phi
\phi:U \to \mathbb{R}^m
Let be a chart with
\mu \in U
\Leftrightarrow
X_n
\Leftrightarrow
smeary
k-
Central limit theorem
Fix
t>0, \enspace M
Riemannian manifold,
X: \Omega \to M.
m-
- (Uniqueness):
- (LLN): satisfies (BCP):
- (Taylor Expansion): There exist
E_t = \{\mu_t\}
\mu_{t,n}\overset{\mathbb{P}}{\to}\mu_t
L_t(\exp_{\mu_t}(x)) = L_t(\exp_{\mu_t}(0)) + \sum_{i=1}^m T_i |(Rx)_i|^r + o(||x||^r)
\geq 2, R\in\text{SO}(m), T_1,...,T_m\neq 0 \text{ st.}
Assume:
(E_{t,n})
(\mu_{t,n})
is
k-
smeary
with
k = \quad-2
r
r
and
\mathscr{L} = \mathcal{N}
The Example
P(X\in \mathbb{L}) = \alpha
P(X = \mu) = 1-\alpha
\mu
What are the log-likelihood means and is the estimator smeary?
\alpha\in [0,1]
t>0
Does the answer depend on and ?
The Fréchet means
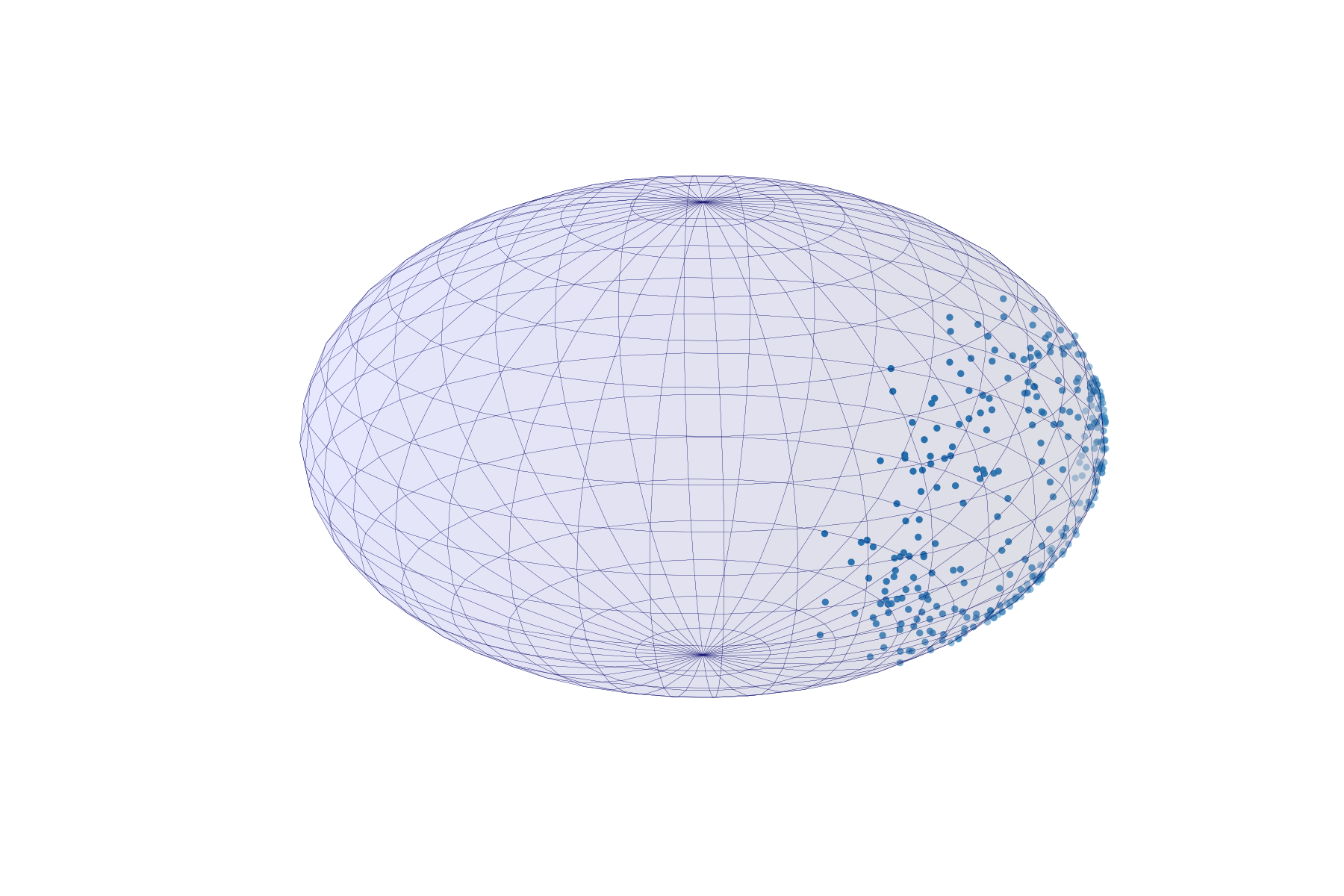
Unique Fréchet mean
and 0-smeary (CLT)
\alpha < 0.56:
Unique Fréchet mean
and 2-smeary
\alpha = 0.56:
Infinitely many means
\alpha > 0.56:
*Stephan Huckemann & Benjamin Eltzner (2018)
\mu
\mu
For there exist
such that
t>0
\alpha(t)
Unique likelihood mean
and 0-smeary (CLT)
\alpha < \alpha(t):
Unique likehood mean
and 2-smeary
\alpha = \alpha(t):
Infinitely many means
\alpha > \alpha(t):
\mu
\mu
The likelihood means
Summary
- (LLN) strong consistency of the likelihood estimator
- (CLT) smeariness of the likelihood estimator with Gaussian limit
- An example of both 0- and 2-smeariness
We have presented sufficient conditions for
Thank you for your attention!
Law of large numbers
Fix
t>0, \enspace M
\mu
\mu_n
\mu_{n-1}
- satisfies (ZC)
- satisfies (BPC) if
compact Riemannian manifold,
X: \Omega \to M
E_t \neq \emptyset
(E_{t,n})
(E_{t,n})
Central limit theorem
Fix
t>0, \enspace M
Riemannian manifold,
X: \Omega \to M
m-
Then for any measurable selection is holds that
\sqrt{n}(V_1,...,V_n)^T \overset{\mathcal{D}}{\to} \mathcal{N}(0,\Sigma)
Assume (Uniqueness), (LLN) and (Taylor Expansion)
(\mu_{t,n})
where
x_n = \log_{\mu_t}\mu_{t,n}
V_i = (Rx_n)_i|(Rx_n)_i|^{r-2}
T=diag(T_1,...,T_m)
\Sigma = \frac{1}{r^2}T^{-1}\text{Cov}[\text{grad}_x(-\ln p(x,X,t))|_{x=0}]T^{-1}
First lunch talk
By pernilleehh
