Asymptotic behavior of Diffusion Means

Pernille E.H. Hansen, Stefan Sommer

University of Copenhagen

Content of talk

  1. Mean values on shape spaces
  2. The BM-maximum likelihood mean
  3. Law of Large Numbers
  4. Central Limit Theorem
  5. Example

Statistics on shape spaces

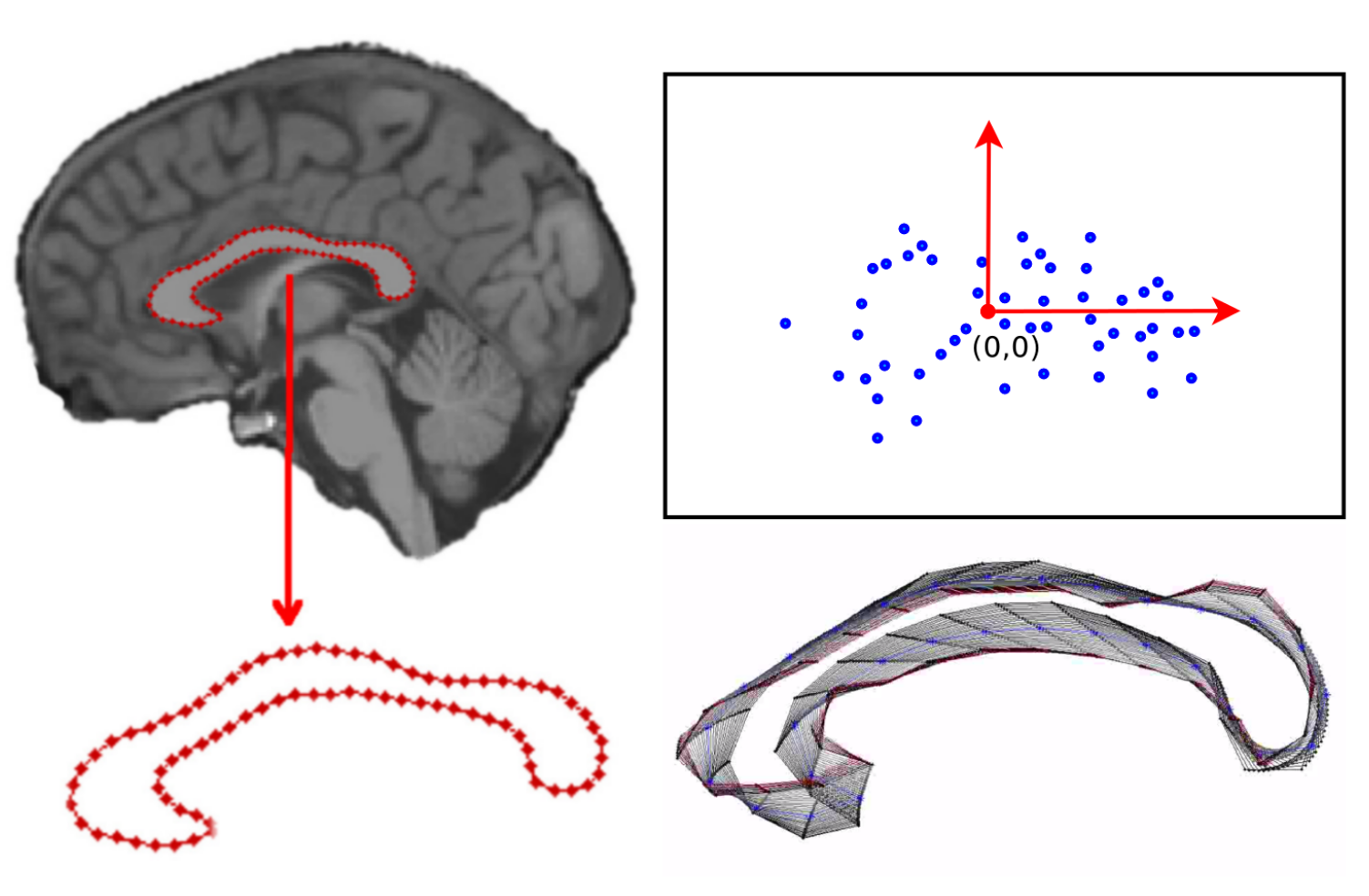
Medical Images

The sphere

\mathcal{S}^2

Manifolds

Mean value?

Y_1,...,Y_N\overset{\text{iid}}{\sim} Y \in
\mu = \mathbb{E}[Y]

Expected value:

Sample estimator:

\mu_N=\frac1N\sum_{i=1}^NY_i

Uniqueness, LLN, CLT

X_1,...,X_N\overset{\text{iid}}{\sim} X \in
\mathbb{R}^n
M
\frac{1}{N} \sum_{i=1}^N X_i, \enspace\mathbb{E}[X]

Fréchet mean

X:\Omega \to M
M = \arg\min_{y\in\mathcal{M}} \mathbb{E}[\text{dist}(y,X)^2]

The Riemann center of mass of a random variable                      is

If                    then      is the Fréchet mean of

M = \{\mu \}
\mu
X.

For                           , the sample Fréchet function

X_1,...,X_N\overset{\text{iid}}{\sim} X
F_N(y) = \frac{1}{N}\sum_{i=1}^{N} \text{dist}(y,X_i)^2
M_N = \arg\min_{y\in M}F_N(y)

and sample Fréchet means

Estimation

Uniqueness, LLN, CLT

Limitation:

  •                    
\text{dist}:M\times M \to \R

is not smooth on all of

M

Diffusion means

Heat kernel on manifolds

p:M \times M \times \mathbb{R}_+ \to \mathbb{R}_+

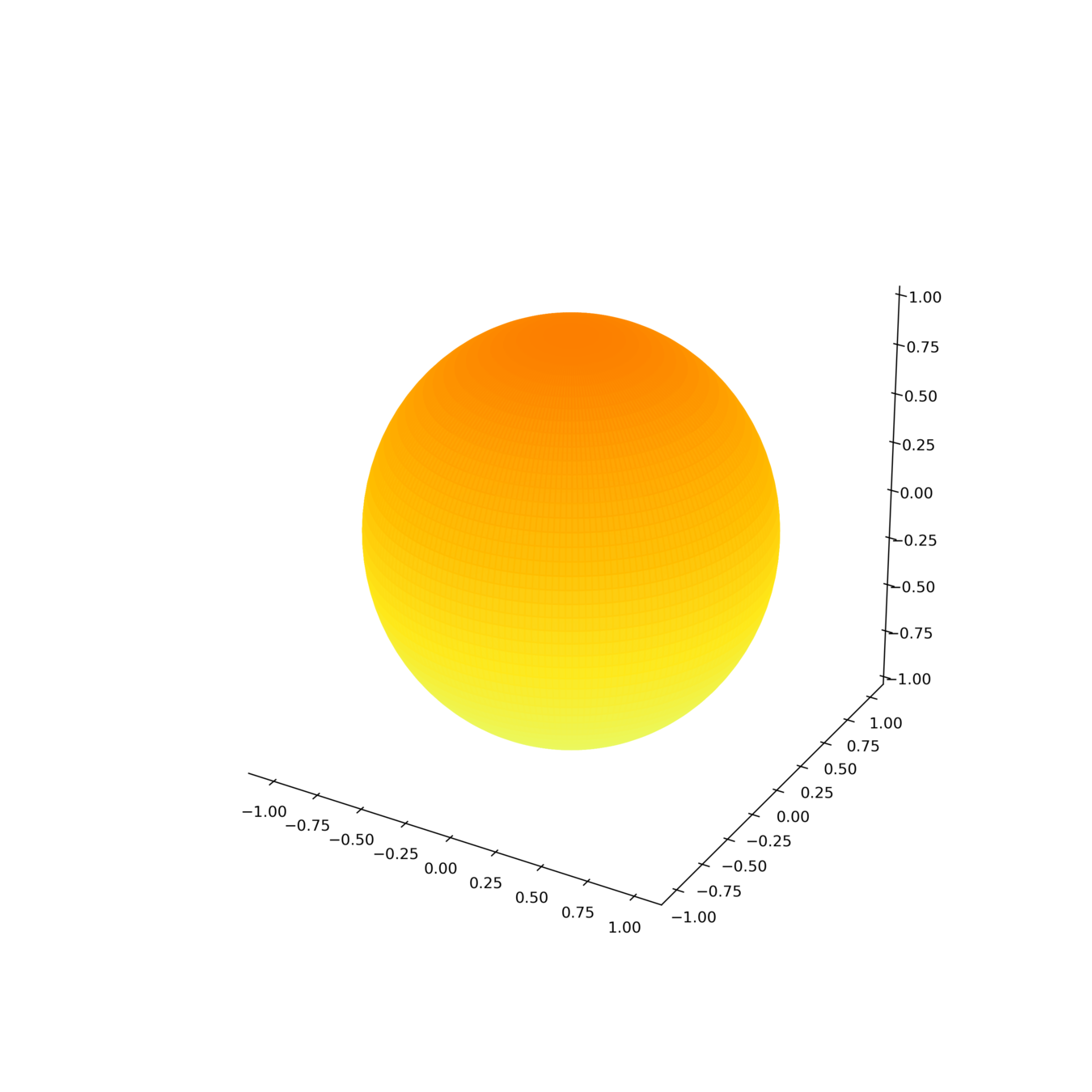
is called a heat kernel on       if


  •  

  •  
  •                                                    
(\partial_t-\Delta_x)p(x,y,t) = 0
\lim_{t\to 0} p(x,y,t)= \delta_x(y)
  • Stochastic completeness
  • M compact

 

t = 0.1
t = 0.5
t = 1

smooth manifold

M

A map 

p \in \mathcal{C}^\infty(M\times M\times \mathbb{R}_+)
M

Limitations

  • Euclidean spaces
  • The hyper spheres
  • Hyperbolic spaces

2) Closed form

1) Existence 

Brownian motion on manifolds

A Brownian motion on       is a Markov process          with transition density function 

p(x,y,t) \approx
\text{"probability" of hitting }y
\text{ in time }t\text{ when starting in }x
p(x,y,t)
(B_t)
M
x
B_t = y
X_1,...,X_n \overset{\text{iid}}{\sim}X\in M

Given

\mu = \arg\max \frac{1}{n} \sum_{i=1}^n \ln(p(x,X_i,t))

most likely origin points of 

(B_t)
\mu = -\arg\min \mathbb{E}_X[\ln p(x,X,t)]

mean point of

X

Diffusion means

X:\Omega \to \mathcal{M}
E_t = \arg\min_{y\in\mathcal{M}} \mathbb{E}[-\text{ln }p(X,y,t)]

For           , the diffusion t-means       of a random variable

are the minimizers of the likelihood function

t>0
E_t
L_t(y) = \mathbb{E}[-\text{ln }p(X,y,t)]
\lim_{t\to 0} -t\ln p (x,y,t) = \frac{\text{dist}(x,y)^2}{2}

Estimation

L_{t,n}(x) = -\frac{1}{N}\sum_{i=1}^N\ln p(x,X_i,t)
E_{t,n} = \arg\min_{x\in M} L_{t,n}(x)

For                            the sample likelihood function is

X_1,...,X_n \overset{\text{iid}}{\sim} X

with sample likelihood means

Can we say something about:

  • (LLN): Convergence of sample means
  • (CLT): Distribution of sample means

Fix

t>0.

Law of large numbers

Fix

t>0.
  • (ZC)  Ziezold if
(E_{t,n})
\cap_{n=1}^\infty \overline{\cup_{k=n}^\infty E_{t,k}} \subset E_t \quad a.s.
  • (BPC) Bhattacharya and Patrangenaru if 
\forall \epsilon>0 \exist n\in \mathbb{N}:
\cup_{k=n}^\infty E_{t,k} \subset B(E_t,\epsilon) \quad a.s.
\mu
\mu_n
\mu_{n-1}

We say that            is a SCE of       in the sense of

E_t

Law of large numbers

Fix

t>0, M
\mu
\mu_n
\mu_{n-1}
  1.             satisfies (ZC) if either
    •     has compact support
    •                                       for all 
  2.             satisfies (BPC) if
    • ​​​          satisfies (ZC)
    • Heine-Borel property of
    • (A coercivity condition)

stoc. complete Riemannian manifold,

X: \Omega \to M
\mathbb{E}[-\ln p (x,X,t)]<\infty
X
x\in M
(E_{t,n})
\overline{\cup_{n=1}^\infty E_{t,n}}
E_t \neq \emptyset
(E_{t,n})
(E_{t,n})

*(Huckemann, 2011)

compact Riemannian manifold

M
  1.           satisfies (ZC)
  2.           satisfies (BPC) if
E_t \neq \emptyset
(E_{t,n})
(E_{t,n})

Central Limit Theorem

and Smeariness

 

Central limit theorem & smeariness

\sqrt{n}\mu_n \overset{\mathcal{D}}{\to} \mathcal{N}(\mu,\Sigma)
X_1,...,X_n \overset{\text{idd}}{\sim} X

on         with

\mathbb{R}^m

smeary:

k-
n^{\frac{1}{2(k+1)}}X_n \overset{\mathcal{D}}{\to} \mathscr{L}

Note: CLT        0-smeary

\Rightarrow
\mathbb{E}[X] = \mu,
\mu_n = \frac{1}{n}\sum_{i=1}^n X_i

CLT:

(X_n)\in \mathbb{R}^m

Central limit theorem & smeariness

(Y_n)
M

smeary

k-

on Riemannian manifold

Define

X_n = \phi(Y_n)-\phi(\mu)\in \R^m

Does it there exist            st                   is                     ?

(\mu_{t,n})
k\geq 0
(Y_n)
k-

smeary

\phi
\phi:U \to \mathbb{R}^m

Let                       be a chart with

\mu \in U
X_n
\Leftrightarrow

smeary

k-

*Stephan Huckemann & Benjamin Eltzner (2018)

Central limit theorem

Fix

t>0, M

stoc. complete Riemannian        manifold,

X: \Omega \to M.
m-
  • (Uniqueness):
  • (LLN):            is a SCE:
  • (Taylor Expansion): There exist
E_t = \{\mu_t\}
\mu_{t,n}\overset{\mathbb{P}}{\to}\mu_t
L_t(\exp_{\mu_t}(x)) = L_t(\exp_{\mu_t}(0)) + \sum_{i=1}^m T_i |(Rx)_i|^r + o(||x||^r)
\geq 2, R\in\text{SO}(m), T_1,...,T_m\neq 0 \text{ st.}

Assume:

(E_{t,n})
(\mu_{t,n})

is

k-

smeary

with

k = \quad-2
r
r

and

\mathscr{L} \sim \mathcal{N}

Two Examples

P(X\in \mathbb{L}) = \alpha
P(X = \mu) = 1-\alpha
\mu

What are the diffusion means and is the estimator smeary?

\alpha\in [0,1]
t>0

Does the answer depend on           and                  ?

\mu
-\mu
P(X = \mu) = 1-\alpha
P(X = -\mu) = \alpha

1.

2.

\mu
-\mu
P(X = \mu) = 1-\alpha
P(X = -\mu) = \alpha

1.

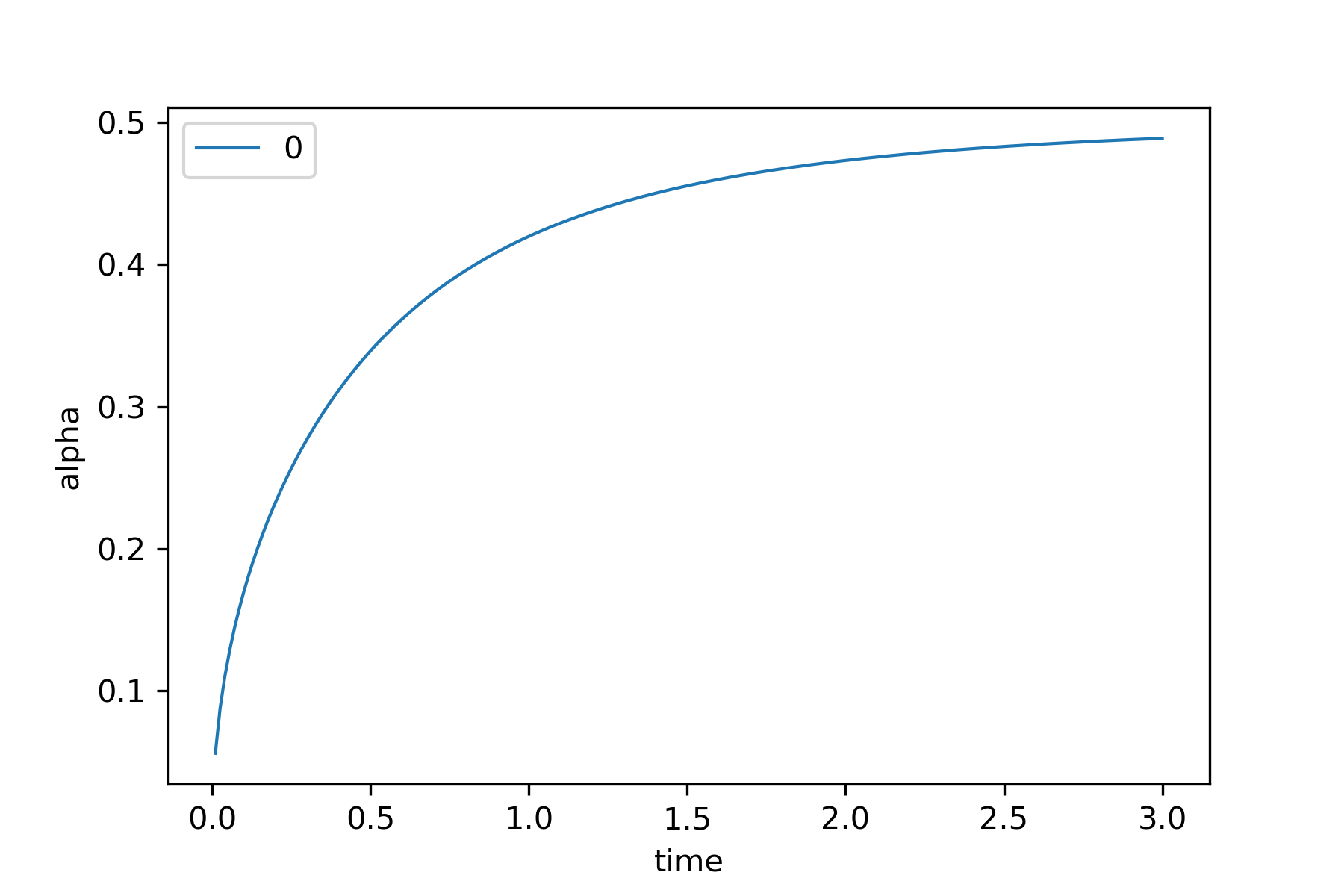
There exist

such that: 

\alpha(t):(0,\infty] \to [0,1]

Unique diffusion mean

and 0-smeary (CLT)

\alpha < \alpha(t):

Unique diffusion mean

and 2-smeary

Infinitely many means

\alpha > \alpha(t):
\alpha = \alpha(t):
\mu
P(X = \mu) = 1-\alpha

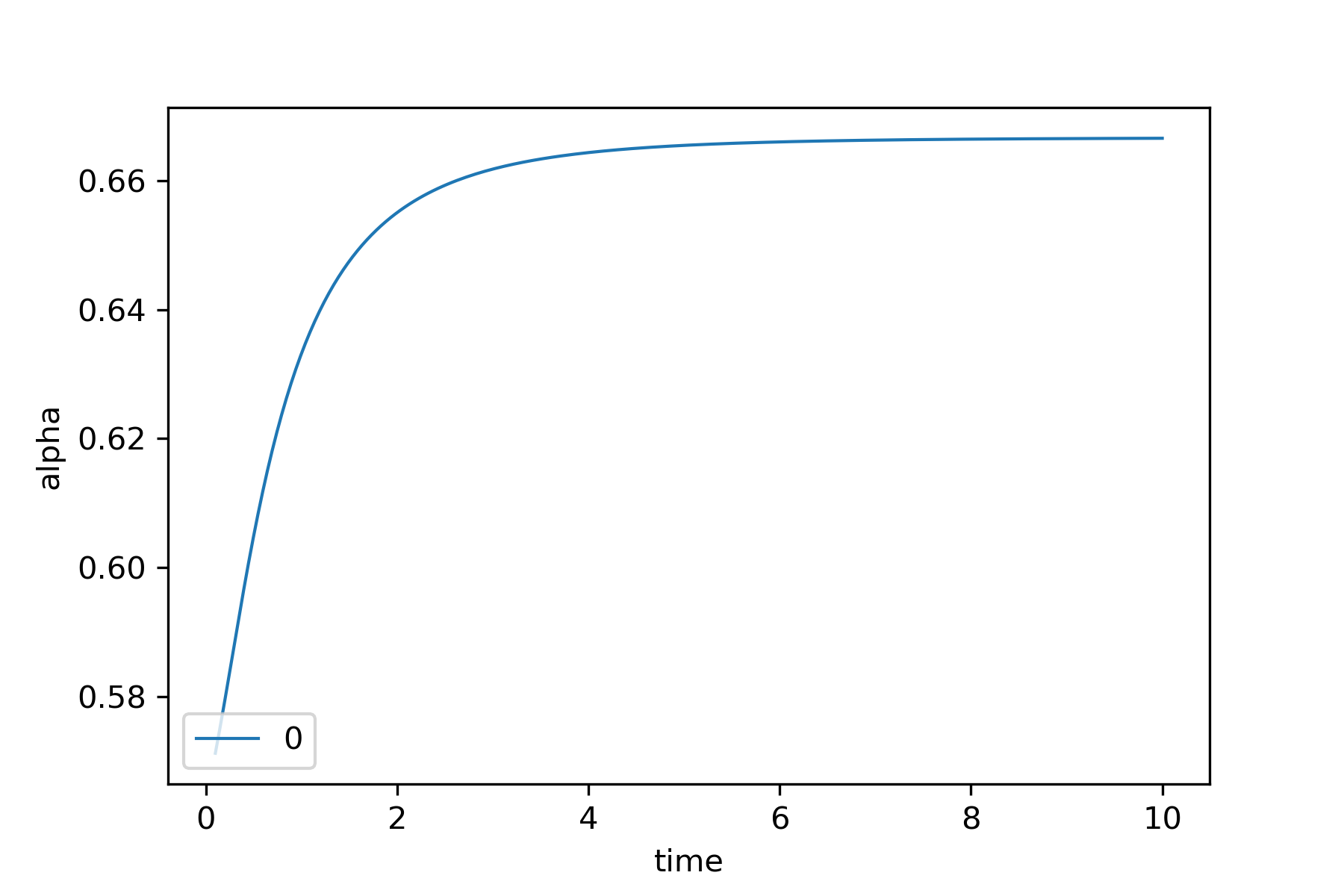
2.

There exist

such that: 

\alpha(t):(0,\infty] \to [0,1]

Unique diffusion mean

and 0-smeary (CLT)

\alpha < \alpha(t):

Infinitely many means

\alpha > \alpha(t):
\alpha = \alpha(t):
P(X\in \mathbb{L}) = \alpha

Estimator is 2-smeary if
diffuion mean is unique

 

The Fréchet means

Unique Fréchet mean

and 0-smeary (CLT)

\alpha < 0.56:

Unique Fréchet mean

and 2-smeary

\alpha \simeq 0.56:

Infinitely many means

\alpha > 0.56:

*Stephan Huckemann & Benjamin Eltzner (2018)

\mu
\mu

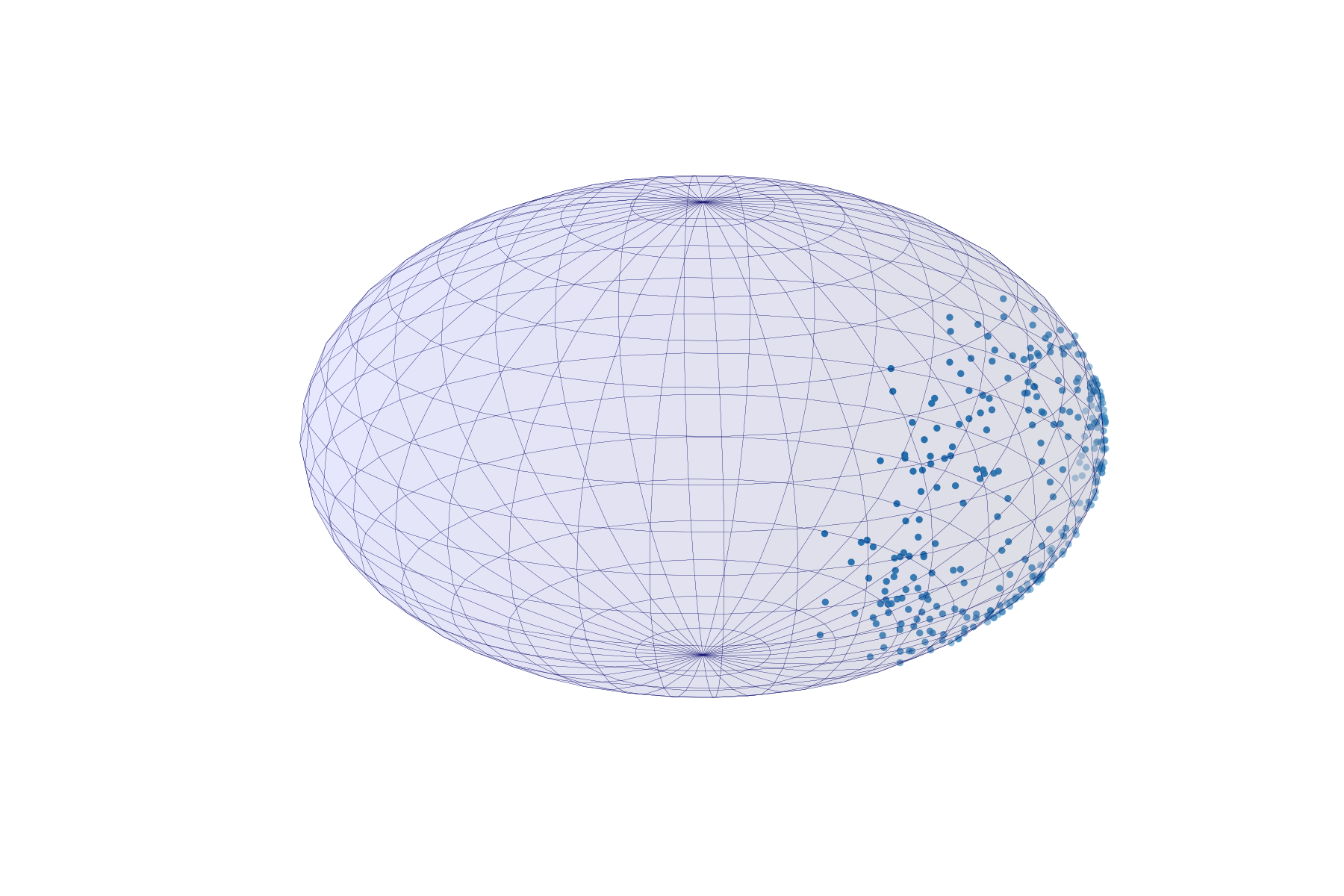
at times of magnetic pole reversal

Magnetic north pole positions








 

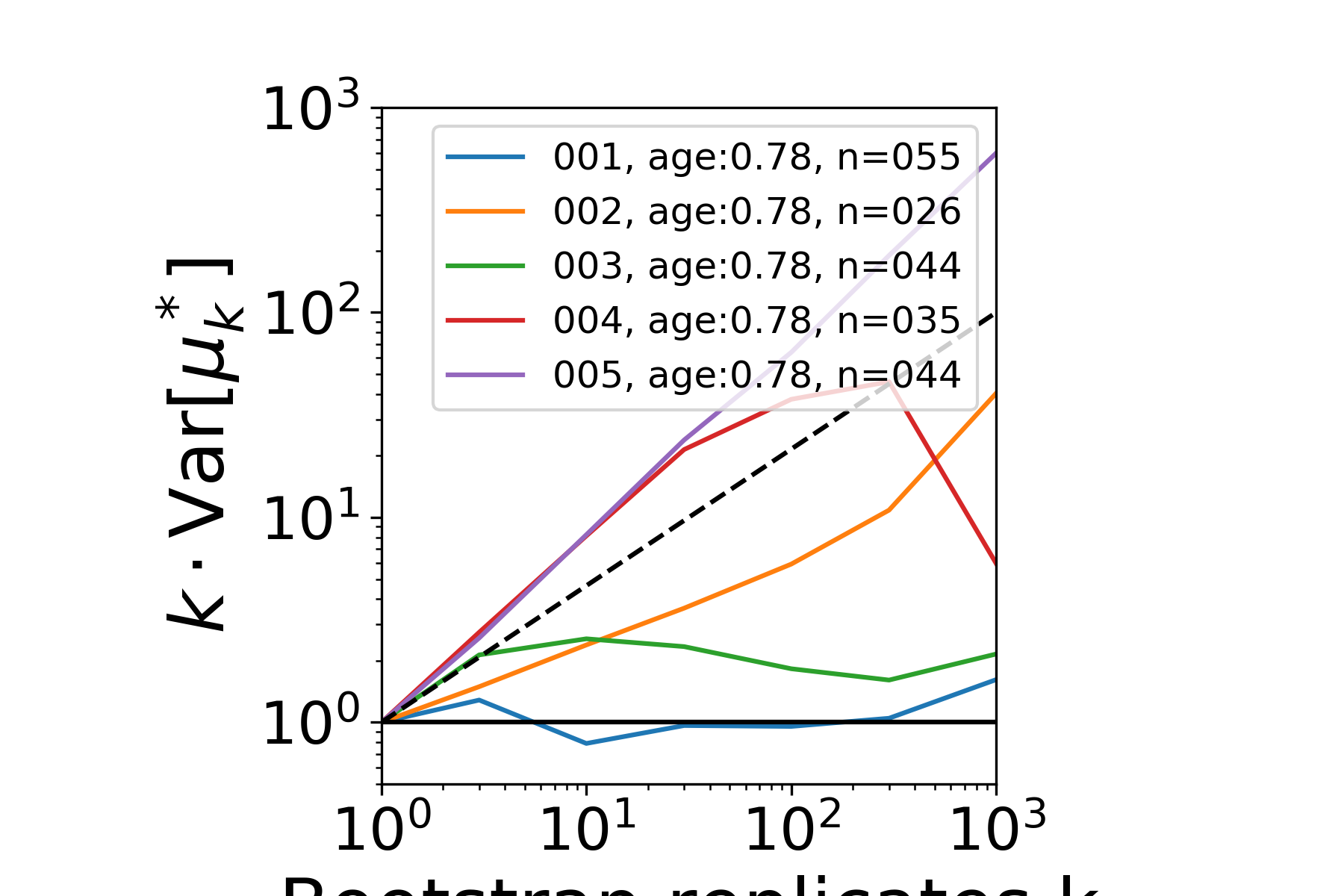
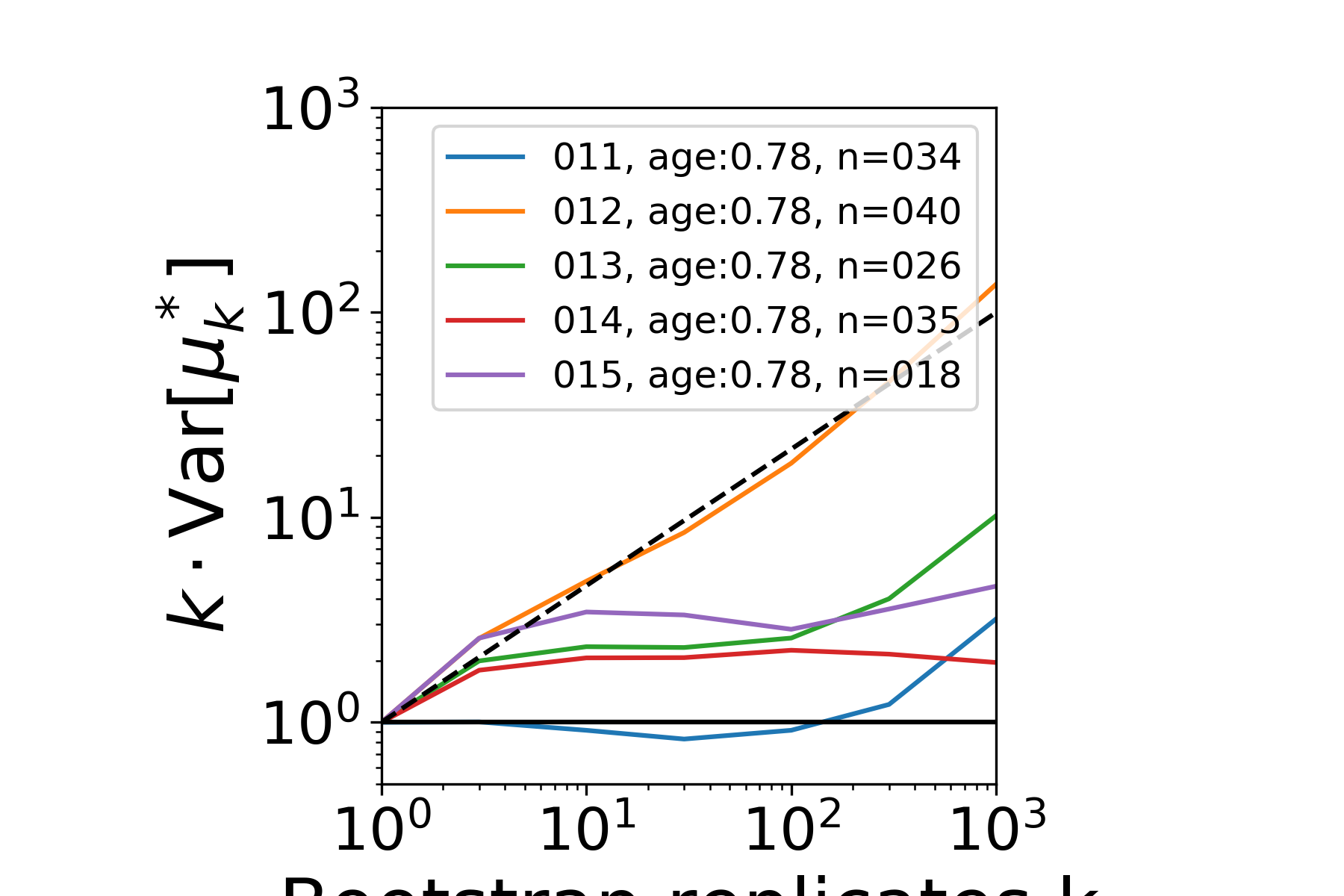
Summary

We have presented

  • An alternative mean value to the Fréchet mean
    • Minimizing smooth function
    • Closed form for heat kernel
  • Sufficient conditions for
    • (LLN) strong consistency of the likelihood estimator
    • (CLT) smeariness of the likelihood estimator with Gaussian limit
  • An example of 0-smeariness
    and 2-smeariness

Thank you for your attention!

[1] Eltzner, Benjamin; Huckemann, Stephan F. A smeary central limit theorem for manifolds with application to high-dimensional spheres. Ann. Statist. 47 (2019), no. 6, 3360--3381. doi:10.1214/18-AOS1781.

 

[2] Huckemann, Stephan F. "INTRINSIC INFERENCE ON THE MEAN GEODESIC OF PLANAR SHAPES AND TREE DISCRIMINATION BY LEAF GROWTH." The Annals of Statistics 39, no. 2 (2011): 1098-124.

Law of large numbers

Fix

t>0, \enspace M
\mu
\mu_n
\mu_{n-1}
  1.           satisfies (ZC)
     
  2.           satisfies (BPC) if

compact Riemannian manifold,

X: \Omega \to M
E_t \neq \emptyset
(E_{t,n})
(E_{t,n})

Central limit theorem

Fix

t>0, \enspace M

Riemannian         manifold,

X: \Omega \to M
m-

Then for any measurable selection           is holds that

\sqrt{n}(V_1,...,V_n)^T \overset{\mathcal{D}}{\to} \mathcal{N}(0,\Sigma)

Assume (Uniqueness), (LLN) and (Taylor Expansion)

(\mu_{t,n})

where

  •  
  •  
  •  
  •  
x_n = \log_{\mu_t}\mu_{t,n}
V_i = (Rx_n)_i|(Rx_n)_i|^{r-2}
T=diag(T_1,...,T_m)
\Sigma = \frac{1}{r^2}T^{-1}\text{Cov}[\text{grad}_x(-\ln p(x,X,t))|_{x=0}]T^{-1}

Seminar Talk: Diffusion means

By pernilleehh

Made with Slides.com

Seminar Talk: Diffusion means

  • 208

More from pernilleehh