Asymptotic behavior of Diffusion Means
Pernille E.H. Hansen, Stefan Sommer
University of Copenhagen
Content of talk
- Mean values on shape spaces
- Diffusion means
- Law of Large Numbers
- Central Limit Theorem
- Example
Statistics on shape spaces
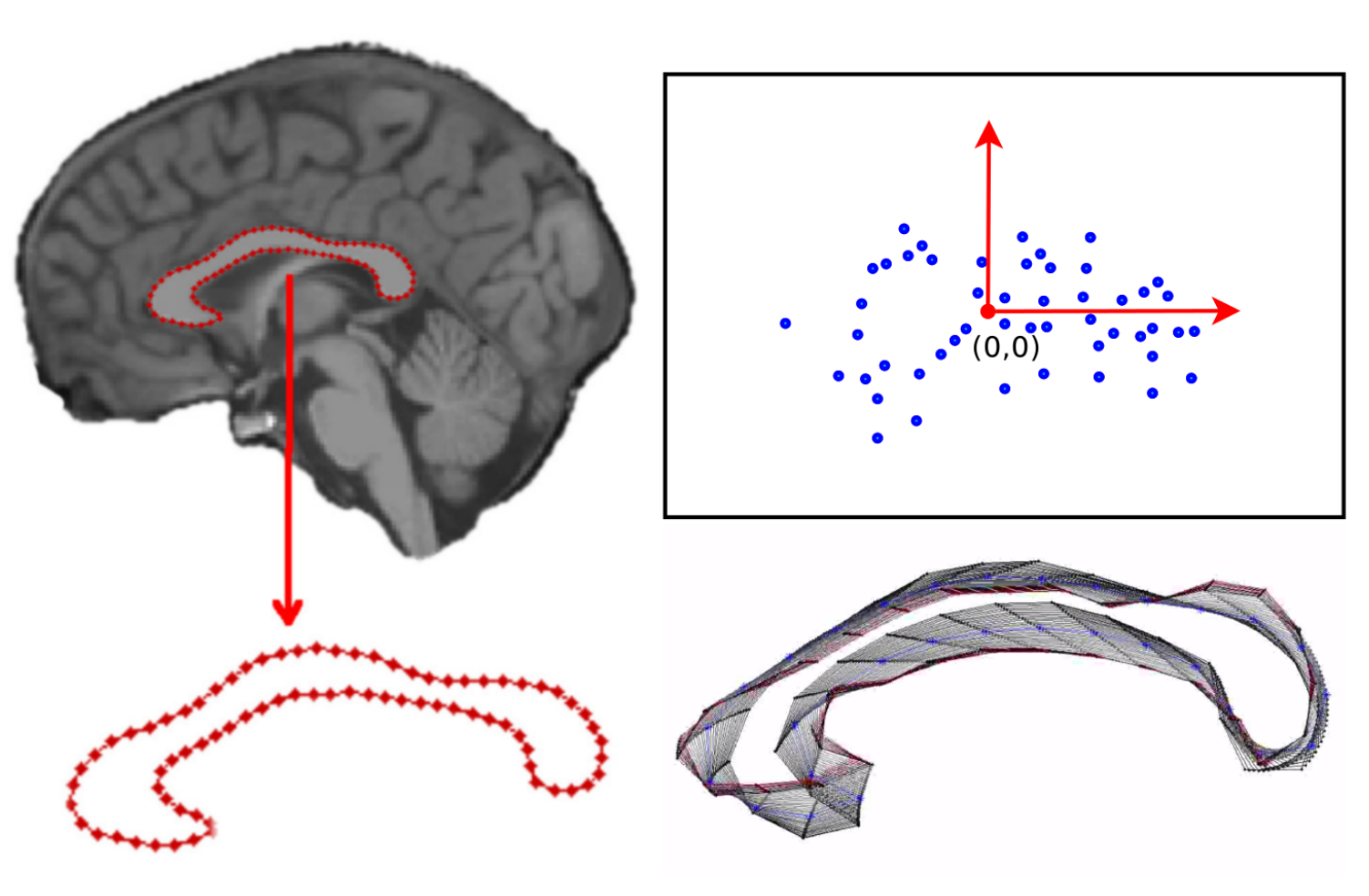
Medical Images
The sphere
\mathcal{S}^2
Manifolds
Mean value?
Y_1,...,Y_N\overset{\text{iid}}{\sim} Y \in
\mu = \mathbb{E}[Y]
Expected value:
Sample estimator:
\mu_N=\frac1N\sum_{i=1}^NY_i
Uniqueness, LLN, CLT
X_1,...,X_N\overset{\text{iid}}{\sim} X \in
\mathbb{R}^n
M
\frac{1}{N} \sum_{i=1}^N X_i, \enspace\mathbb{E}[X]
Fréchet mean
X:\Omega \to M
M = \arg\min_{y\in\mathcal{M}} \mathbb{E}[\text{dist}(y,X)^2]
The Riemann center of mass of a random variable is
If then is the Fréchet mean of
M = \{\mu \}
\mu
X.
For , the sample Fréchet function
X_1,...,X_N\overset{\text{iid}}{\sim} X
F_N(y) = \frac{1}{N}\sum_{i=1}^{N} \text{dist}(y,X_i)^2
M_N = \arg\min_{y\in M}F_N(y)
and sample Fréchet means
Estimation
Uniqueness, LLN, CLT
Limitation:
\text{dist}:M\times M \to \R
is not smooth on all of
M
Diffusion means
Heat kernel on manifolds
p:M \times M \times \mathbb{R}_+ \to \mathbb{R}_+
is called a heat kernel on if
(\partial_t-\Delta_x)p(x,y,t) = 0
\lim_{t\to 0} p(x,y,t)= \delta_x(y)
- Stochastic completeness
- M compact
t = 0.1
t = 0.5
t = 1
smooth manifold
M
A map
p \in \mathcal{C}^\infty(M\times M\times \mathbb{R}_+)
M
Limitations
- Euclidean spaces
- The hyper spheres
- Hyperbolic spaces
2) Closed form
1) Existence
Brownian motion on manifolds
A Brownian motion on is a Markov process with transition density function
p(x,y,t) \approx
\text{"probability" of hitting }y
\text{ in time }t\text{ when starting in }x
p(x,y,t)
(B_t)
M
x
B_t = y
X_1,...,X_n \overset{\text{iid}}{\sim}X\in M
Given
\mu = \arg\max \frac{1}{n} \sum_{i=1}^n \ln(p(x,X_i,t))
most likely origin points of
(B_t)
\mu = -\arg\min \mathbb{E}_X[\ln p(x,X,t)]
mean point of
X
Diffusion means
X:\Omega \to \mathcal{M}
E_t = \arg\min_{y\in\mathcal{M}} \mathbb{E}[-\text{ln }p(X,y,t)]
For , the diffusion t-means of a random variable
are the minimizers of the likelihood function
t>0
E_t
L_t(y) = \mathbb{E}[-\text{ln }p(X,y,t)]
\lim_{t\to 0} -t\ln p (x,y,t) = \frac{\text{dist}(x,y)^2}{2}
Estimation
L_{t,n}(x) = -\frac{1}{N}\sum_{i=1}^N\ln p(x,X_i,t)
E_{t,n} = \arg\min_{x\in M} L_{t,n}(x)
For the sample likelihood function is
X_1,...,X_n \overset{\text{iid}}{\sim} X
with sample likelihood means
Can we say something about:
- (LLN): Convergence of sample means
- (CLT): Distribution of sample means
Fix
t>0.
Law of large numbers
Fix
t>0.
(E_{t,n})
\forall \epsilon>0 \exist n\in \mathbb{N}:
\cup_{k=n}^\infty E_{t,k} \subset B(E_t,\epsilon) \quad a.s.
\mu
\mu_n
\mu_{n-1}
We say that is a strongly consistent estimator of if
E_t
Diffusion estimator is a SCE on
compact Riemannian manifolds!
Central Limit Theorem
and Smeariness
\sqrt{n}(\mu_n-\mu) \overset{\mathcal{D}}{\to} \mathcal{N}(\mu,\Sigma)
CLT:
smeary:
k-
n^{\frac{1}{2(k+1)}}(\mu_n-\mu) \overset{\mathcal{D}}{\to} \mathscr{L}
Note: CLT 0-smeary
\Rightarrow
Central limit theorem & smeariness
(Y_n)
M
smeary
k-
on Riemannian manifold
Define
X_n = \phi(Y_n)-\phi(\mu)\in \R^m
Does it there exist st is ?
(\mu_{t,n})
k\geq 0
(Y_n)
k-
smeary
\phi
\phi:U \to \mathbb{R}^m
Let be a chart with
\mu \in U
X_n
\Leftrightarrow
smeary
k-
*Stephan Huckemann & Benjamin Eltzner (2018)
Central limit theorem
Fix
t>0, M
stoc., compact Riemannian manifold,
X: \Omega \to M.
m-
- Uniqueness of
- Existence of Taylor Expansion of log-likelihood function of order
E_t = \{\mu_t\}
Assume:
(\mu_{t,n})
is
k-
smeary
with
k = \quad-2
r
and
\mathscr{L} \sim \mathcal{N}
r\geq 2
Example
What are the diffusion means and is the estimator smeary?
\alpha\in [0,1]
t>0
Does the answer depend on and ?
\mu
-\mu
\cdot \enspace P(X = \mu) = 1-\alpha
\cdot \enspace P(X = -\mu) = \alpha
X: \Omega \to \mathcal{S}^m
\mu
-\mu
P(X = \mu) = 1-\alpha
P(X = -\mu) = \alpha
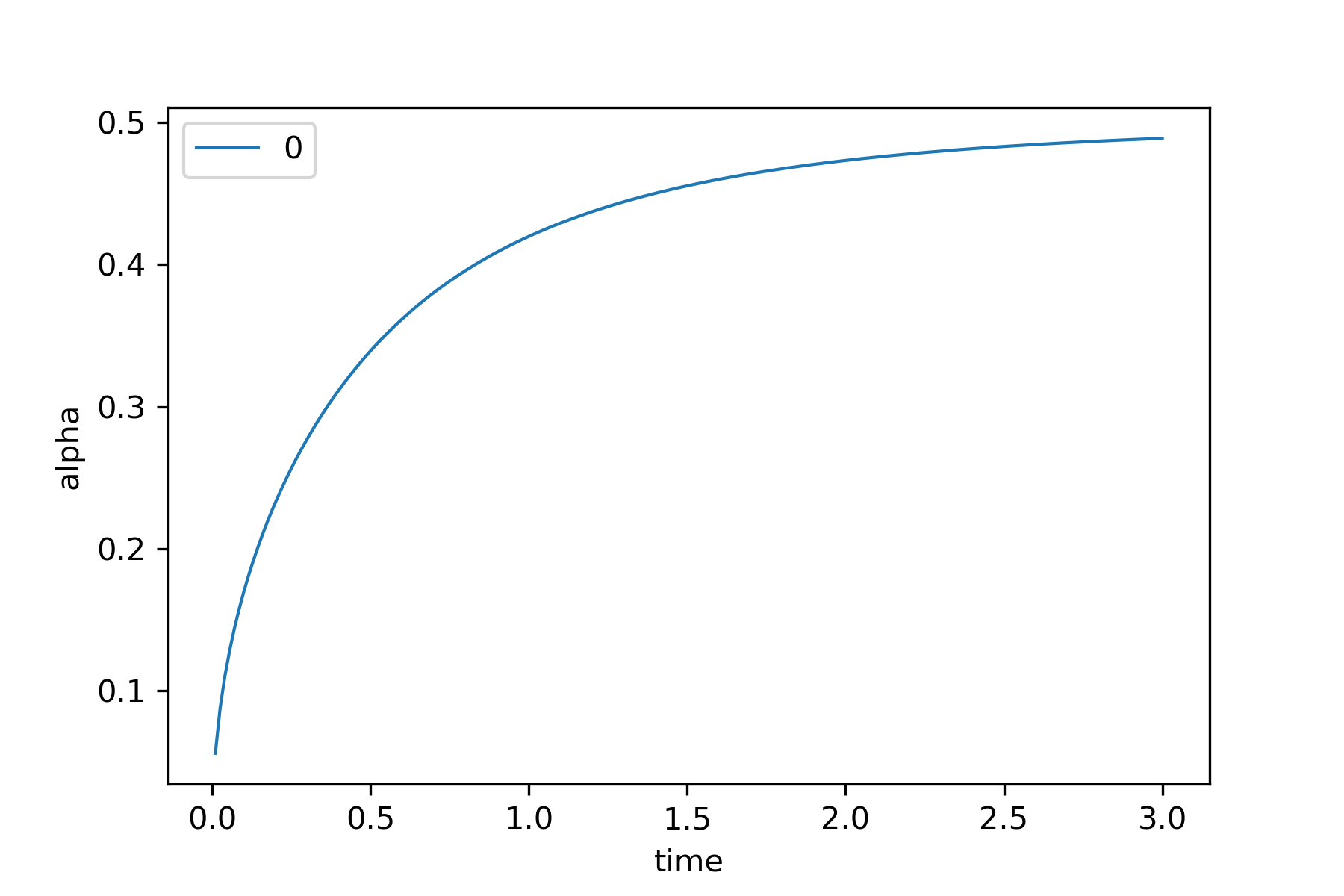
For each and
there exist such that:
\alpha_m(t)
Unique diffusion mean
and 0-smeary (CLT)
\alpha < \alpha_m(t):
Unique diffusion mean
and 2-smeary
Infinitely many means
\alpha > \alpha_m(t):
\alpha = \alpha_m(t):
m\geq 2
t> \log(8(m+2)/m)/2 \leq 0.562
at times of magnetic pole reversal
Magnetic north pole positions
|
|
|---|
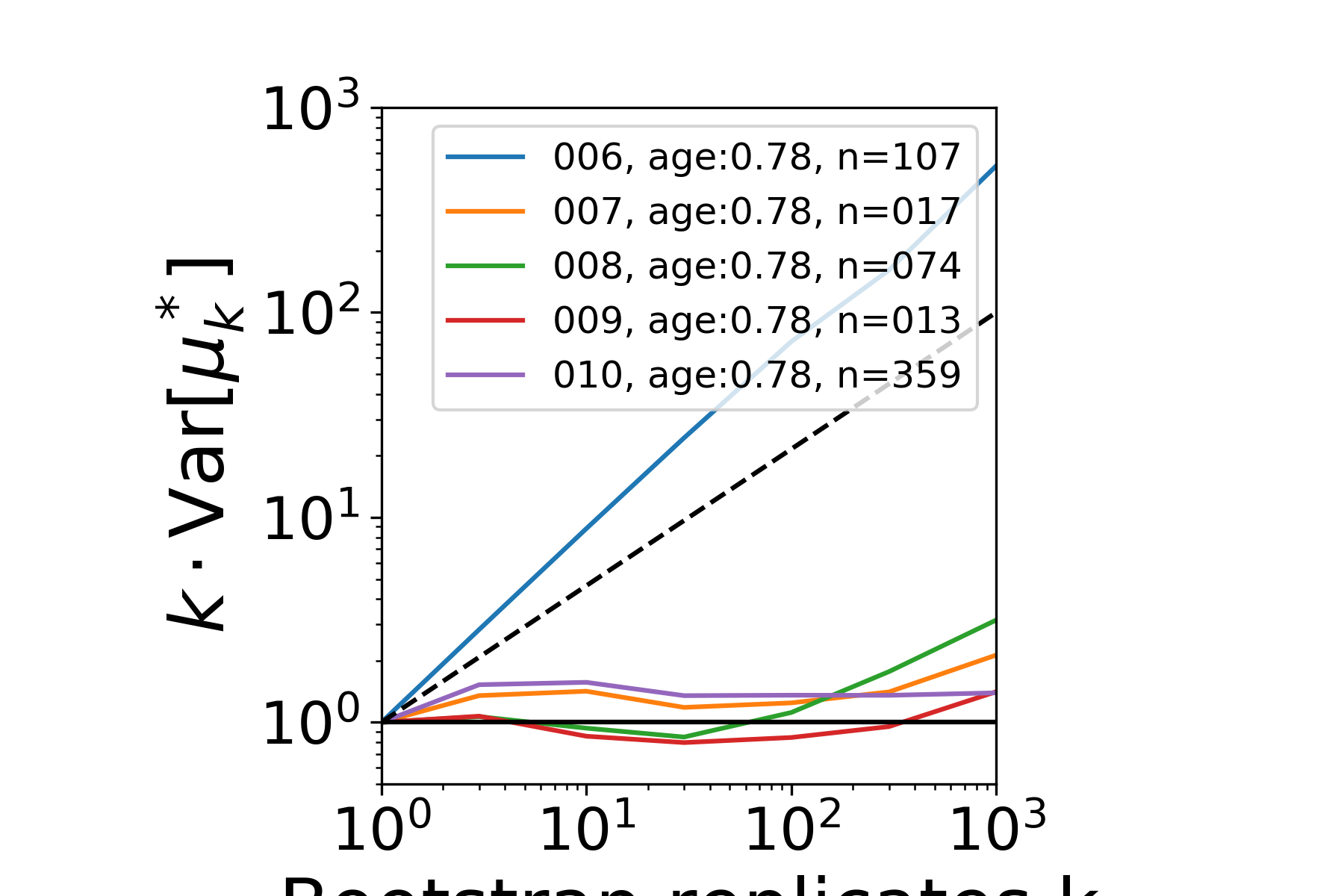
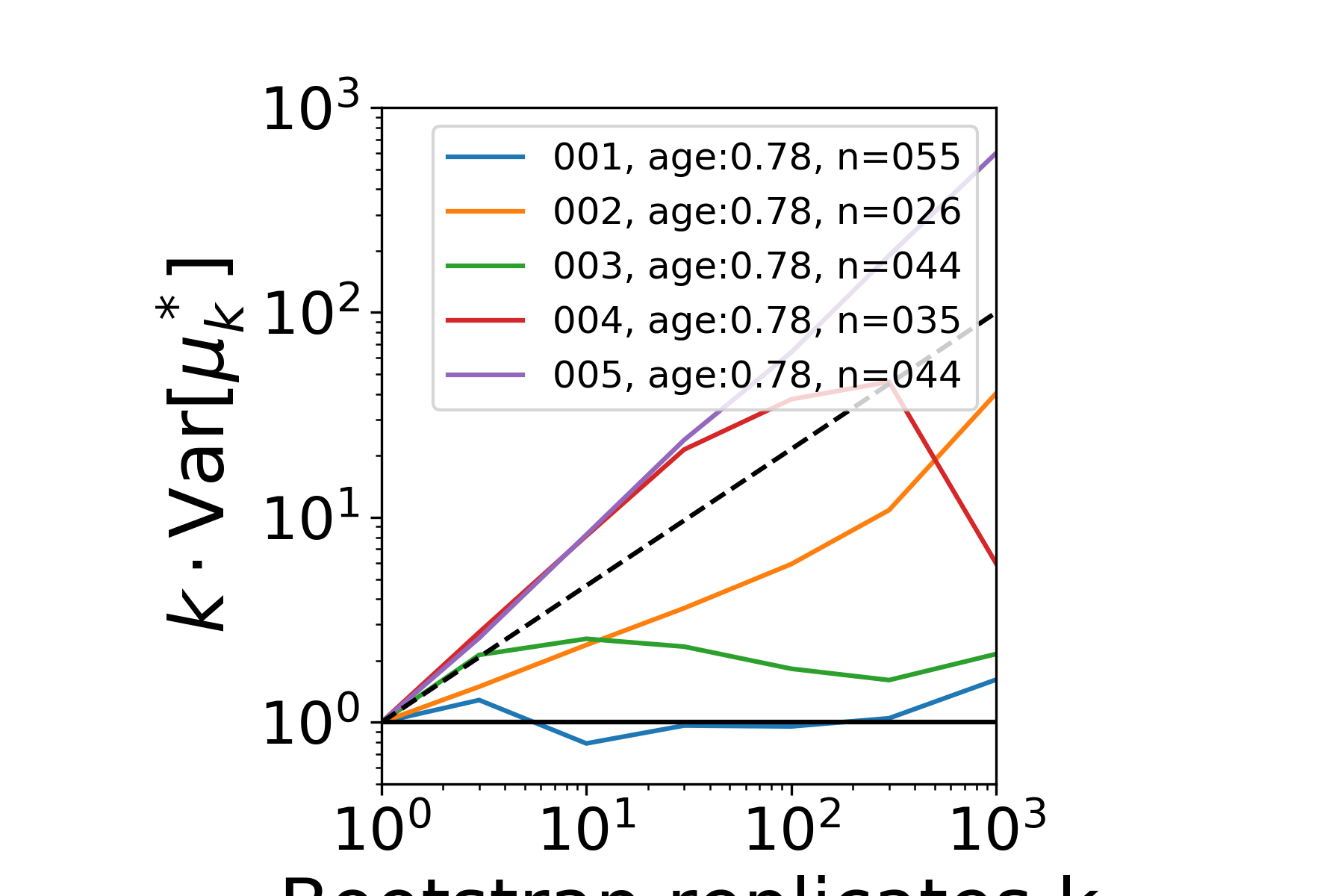
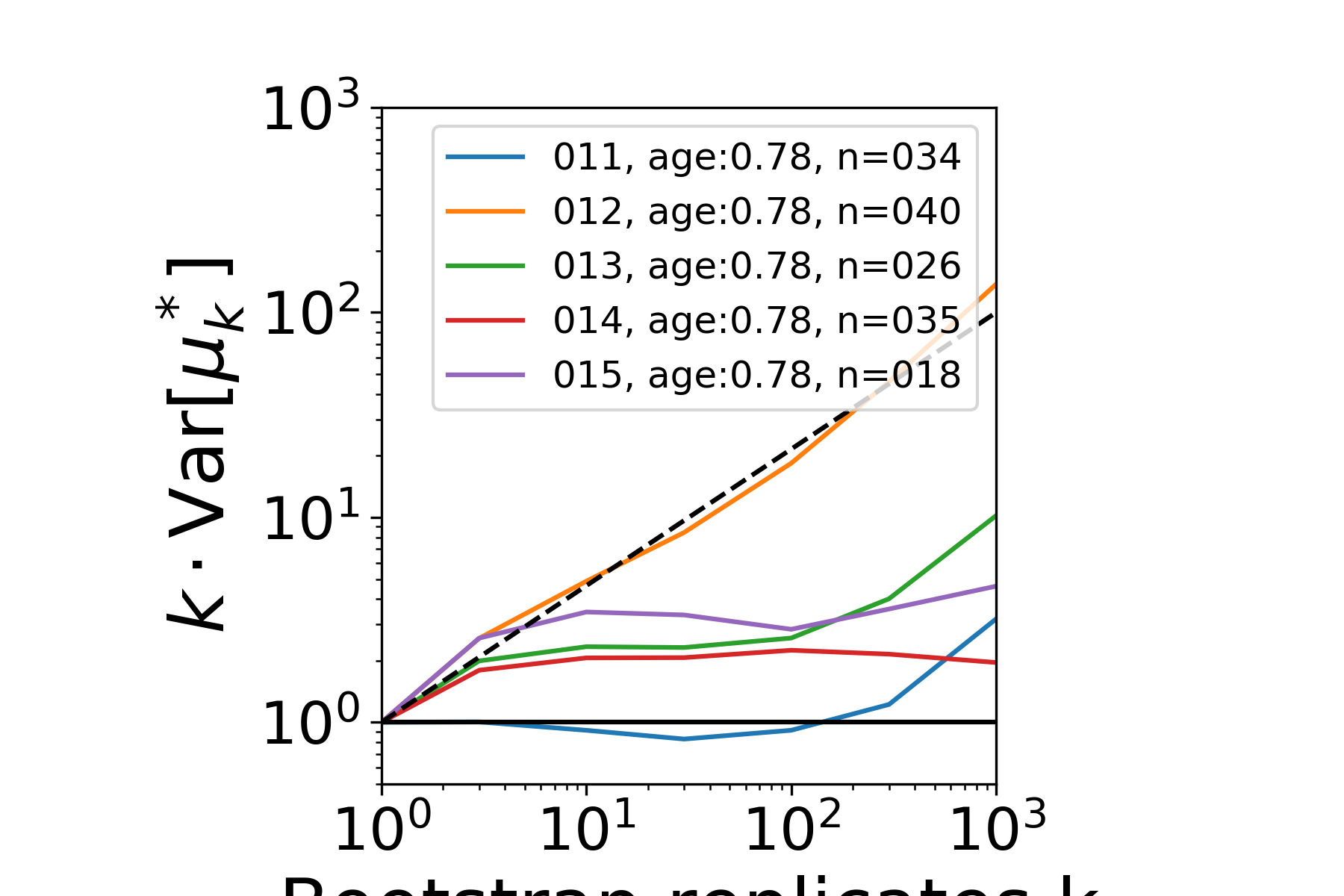
Summary
We have presented
- An alternative mean value to the Fréchet mean
- Minimizing smooth function
- Closed form for heat kernel
- (LLN) strong consistency of the likelihood estimator
- (CLT) smeariness of the likelihood estimator with Gaussian limit
- An example of 0-smeariness
and 2-smeariness - Next step: Estimating t
Thank you for your attention!
[1] Eltzner, Benjamin; Huckemann, Stephan F. A smeary central limit theorem for manifolds with application to high-dimensional spheres. Ann. Statist. 47 (2019), no. 6, 3360--3381. doi:10.1214/18-AOS1781.
[2] Huckemann, Stephan F. "INTRINSIC INFERENCE ON THE MEAN GEODESIC OF PLANAR SHAPES AND TREE DISCRIMINATION BY LEAF GROWTH." The Annals of Statistics 39, no. 2 (2011): 1098-124.
Lunch Talk: Diffusion means
By pernilleehh
