DP
定義
能以Dynamic Programming (簡稱 DP) 求解,該問題含有以下三個性質:
1. 最優子結構
2. 重複子問題
3. 無後效性
常見的dp題目 : 費氏數列 路徑總數 最長共同子序列 背包問題...等
大問題
子問題
子問題
子問題
舉個栗子🌰
-硬幣找零問題
題目 : 要買價值 15 元的商品,要求花最少的硬幣數。
10 元、5 元、1 元硬幣
-> 貪心策略 : 每次用額面較大的硬幣去付10*1+5*1+1*0=15
11 元、5 元、1 元硬幣 -> dp
設 f(x) 為價值 x 元的商品所需要的最少硬幣數
-選11元則可能 f(15)=f(4)+1
-選5元則可能 f(15)=f(10)+1
-選1 元則可能 f(15) = f(14) + 1
f(x) = min{ f(x-11), f(x-5), f(x-1) } + 1
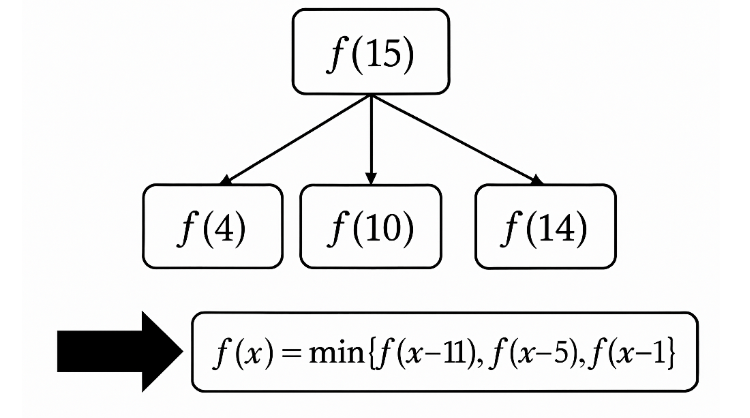
1.最優子結構
f(x) 的定義為湊出 x 元的最少硬幣數,最少即 f(x) 的最優解,而 f(x) 仰賴 3 個子問題的最優解
2.無後效性
若求出了 f(4)=4,則不管未來要求任何 f(t) 的解都不會改f(4) 的解
3.重複子問題
若求 f(9) 則需要先求解 f(8),f(4)
f(4) 在之前可能已經找到解了就無需再為 f(9) 重新計算
費式數列
費氏數列 -> 遞迴 -> 記憶體會不夠 (時間複雜度O(φⁿ))
dp -> 建立「陣列」去儲存已經計算過的數字 (時間複雜度O(N))
「以空間換取時間」
假設n=7
| f(7) | f(6) | f(5) | f(4) | f(3) | f(2) | f(1) |
| 13 | 8 | 5 | 3 | 2 | 1 | 1 |
f(7)
f(6)
f(5)
f(5)
f(4)
f(4)
f(3)
f(3)
f(3)
f(3)
f(2)
f(4)
f(2)
f(2)
f(1)
#include<iostream>
using namespace std;
#define MAX 100
long long fib( long long num )
{
long long dp[num + 1];
dp[0] = 0;
dp[1] = 1;
for(int i = 2; i < num+1; ++i)
{
dp[i] = dp[i-1] + dp[i-2];
}
return dp[num];
}
int main()
{
long long num = 0;
cin >> num;
cout << fib(num) << endl;
return 0;
}費事數列變形-爬樓梯
今天體育課地點在禮堂樓上的體育館,你爬到上面需要10步才能到達頂部。每次你可以爬 1 或 2 級台階。則你可以透過多少種不同的方式登上頂峰?
費事數列變形-爬樓梯
今天體育課地點在禮堂樓上的體育館,你爬到上面需要10步才能到達頂部。每次你可以爬 1 或 2 級台階。則你可以透過多少種不同的方式登上頂峰?
or
f(7)
f(6)
f(5)
f(5)
f(4)
f(4)
f(3)
f(3)
f(3)
f(3)
f(2)
f(4)
f(2)
f(2)
f(1)
#include <iostream>
using namespace std;
int main() {
const int n = 10;
int dp[n + 1]; // dp[i] 表示爬到第 i 階的方法數
dp[0] = 1; // 一開始在第 0 階,有 1 種方式(不動)
dp[1] = 1; // 第 1 階只能一步上來
for (int i = 2; i <= n; ++i) {
dp[i] = dp[i - 1] + dp[i - 2]; // 來自前一階或前兩階
}
cout << "到達第 " << n << " 階的方法數為:" << dp[n] << endl;
return 0;
}
路徑計算
給定一個大小為3 * 4的地圖,一名機器人從工廠出發往家走,只能往右或下走,每格數字代表行經該格的路徑長,請問走到右下角累計消耗的最短路徑是多少?
🏙️ 7 8 9
1 2 5 1
1 4 10 🏡
🏙️ 7 8 9
1 2 5 1
1 4 10 🏡
🏙️ 7 8 9
1 2 5 1
1 4 10 🏡
🏙️ 7 15 9
1 2 5 1
1 4 10 🏡
🏙️ 7 15 24
1 2 5 1
1 4 10 🏡
🏙️ 7 15 24
1 2 5 1
1 4 10 🏡
🏙️ 7 15 24
1 2 5 1
2 4 10 🏡
🏙️ 7 15 24
1 3 5 1
2 4 10 🏡
🏙️ 7 15 24
1 3 8 1
2 4 10 🏡
🏙️ 7 15 24
1 3 8 9
2 4 10 🏡
🏙️ 7 15 24
1 3 8 9
2 6 10 🏡
🏙️ 7 15 24
1 3 8 9
2 6 16 🏡
🏙️ 7 15 24
1 3 8 9
2 6 16 🏡
#include<bits/stdc++.h>
using namespace std;
int main() {
// 地圖資料(每格代表通過該格的消耗)
int grid[3][4] = {
{0, 7, 8, 9},
{1, 2, 5, 1},
{1, 4, 10, 0}
};
// DP 表:紀錄到每個格子的最短路徑和
int dp[3][4];
// 起點
dp[0][0] = grid[0][0];
// 第一列只能從左邊來
for (int j = 1; j < 4; j++) {
dp[0][j] = dp[0][j - 1] + grid[0][j];
}
// 第一欄只能從上面來
for (int i = 1; i < 3; i++) {
dp[i][0] = dp[i - 1][0] + grid[i][0];
}
// 其他格子從上方或左方來,取較小的路徑和
for (int i = 1; i < 3; i++) {
for (int j = 1; j < 4; j++) {
dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
}
}
// 結果
cout << "最短路徑總和為:" << dp[2][3] << endl;
return 0;
}
DP
By phoebe tsai
DP
- 182



