Exploration by Random Network Distillation
Piotr Kozakowski
Montezuma’s Revenge
Exploration problem
We want our policy to make good actions to maximize the reward (exploitation).
But to know which actions are good, we need to explore the state space (exploration).
Intrinsic rewards: overview
Idea: Add a reward for exploring new states.
where is reward from the environment (extrinsic)
and is a reward for exploration (intrinsic).
r_t = e_t + i_t
e_t
i_t
Intrinsic rewards: count-based
where is the number of times we've seen state s.
i_t = \frac{1}{n_t(s_t)}
n_t(s)
Bellemare et al. - Unifying count-based exploration and intrinsic motivation (2016)
Intrinsic rewards: count-based
where is the number of times we've seen state s.
Problem: Large state space.
i_t = \frac{1}{n_t(s_t)}
n_t(s)
Bellemare et al. - Unifying count-based exploration and intrinsic motivation (2016)
Intrinsic rewards: count-based
where is the number of times we've seen state s.
Problem: Large state space.
Solution: Use function approximation! But how?
i_t = \frac{1}{n_t(s_t)}
n_t(s)
Bellemare et al. - Unifying count-based exploration and intrinsic motivation (2016)
Function approximators in RL
Usually used as maps:
Now we need a (multi)set:
Q[s, a] = ~?
s \stackrel{?}{\in} S_e
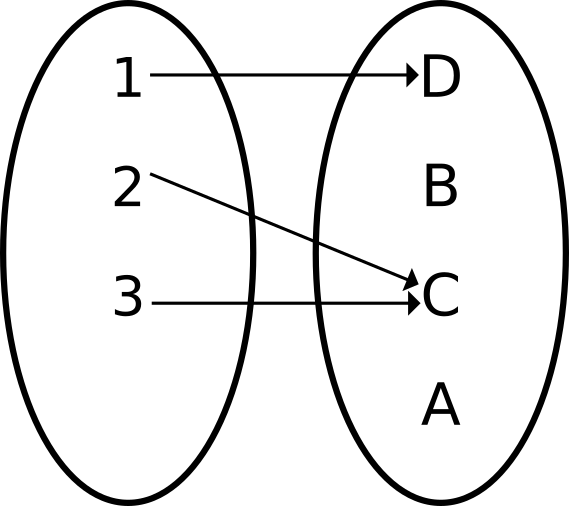
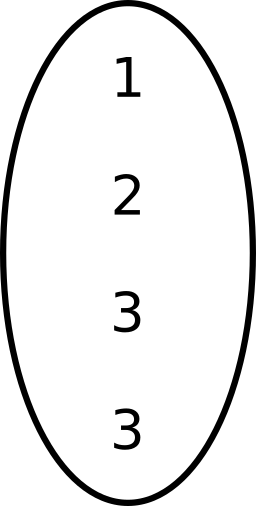
Intrinsic rewards: prior work
Prediction error of various models has previously been used as intrinsic reward:
- Forward dynamics
- Inverse dynamics
- Constant zero function
(s, a) \rightarrow (s', r)
(s, s') \rightarrow a
s \rightarrow 0
- Stadie et al. - Incentivizing exploration in reinforcement learning with deep predictive models (2015)
- Pathak et al. - Curiosity-driven exploration by self-supervised prediction (2017)
- Fox et al. - Dora the explorer: Directed outreaching reinforcement action-selection (2018)
Random Network Distillation
Two networks with the same architecture:
- target network with fixed, random weights
- predictor network trained to approximate
is updated in each visited state.
Prediction error is used as intrinsic reward:
S \rightarrow \mathbb{R}^k
f
\hat{f}
f
\hat{f}
i_t = |\hat{f}(s_t) - f(s_t)|^2
Burda et al. - Exploration by random network distillation (2018)
Example: novelty detection on MNIST
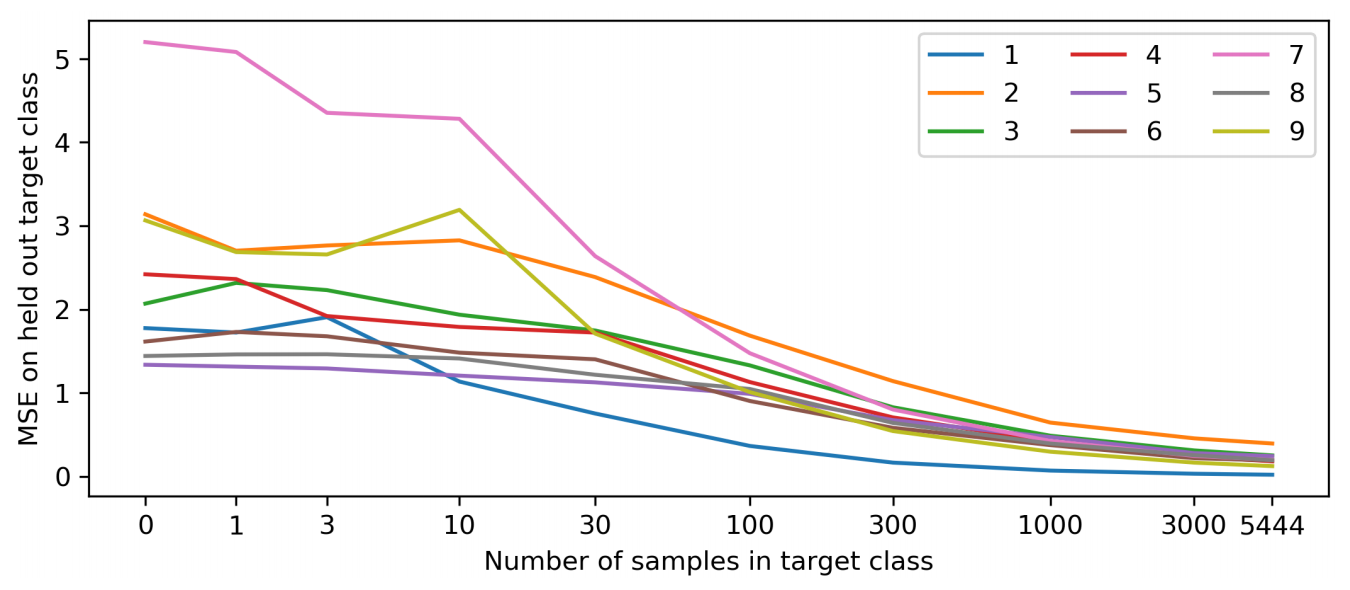
Why does it work?
Sources of uncertainty
- Too little training data (epistemic uncertainty)
- Stochasticity of the target function (aleatoric uncertainty)
- Insufficient capacity of the model
- Learning dynamics
Sources of uncertainty
- Too little training data (epistemic uncertainty)
- Stochasticity of the target function (aleatoric uncertainty)
- Insufficient capacity of the model
- Learning dynamics
Sources of uncertainty
- Too little training data (epistemic uncertainty)
- Stochasticity of the target function (aleatoric uncertainty)
- Insufficient capacity of the model
- Learning dynamics
Forward dynamics measures 1, but also 2 and 3.
RND measures 1, but not 2 and 3.
4 is hard to avoid.
Bayesian deep learning
Goal: Measure uncertainty of prediction of our neural network (for regression).
Instead of one model, learn a distribution over models.
During inference, report mean and variance of prediction over the model distribution.
Bayesian deep learning
Start from a prior distribution
Update using examples from the dataset
to get a posterior distribution
i.e. find
P(\theta)
D
P(\theta | D)
\text{argmax}_\theta P(\theta | D) = \text{argmax}_\theta \frac{P(D | \theta) P(\theta)}{P(D)}
= \text{argmax}_\theta P(D | \theta) P(\theta)
Bayesian linear regression
\text{Let}~ \theta \in \mathbb{R}^d ~\text{with prior}~ \theta \sim N(0, \lambda I), D = \{(x_i, y_i)\}_{i=1}^n ~\text{for}~ x_i \in \mathbb{R}^d,
\tilde{\theta} + \text{argmin}_\theta \sum_{i=1}^n |\tilde{y_i} - (f_{\tilde{\theta}} + f_{\theta})(x_i)|^2 + \frac{\sigma^2}{\lambda} |\theta|^2
y_i = \theta^T x_i + \epsilon_i ~\text{with}~ \epsilon_i \sim N(0, \sigma^2) ~\text{iid}, f_\theta(x) = x^T\theta, \tilde{y_i} \sim N(y_i, \sigma^2),
\tilde{\theta} \sim N(0, \lambda I). ~\text{Then the following optimization generates a sample}
Empirical results with DQN translate to neural networks.
Osband et al. - Randomized prior functions for deep reinforcement learning (2018)
\theta | D:
Bayesian linear regression vs RND
\text{argmin}_\theta \sum_{i=1}^n |(f_{\tilde{\theta}} + f_{\theta})(x_i)|^2
\sigma^2 = 0, y_i = 0
which is equivalent to training the predictor in RND when the target is sampled from the prior (need to flip the sign).
The minimized error averaged over an ensemble with shared weights - approximation of prediction uncertainty - is our intrinsic reward.
Let - fitting the zero function without noise. Then the optimization of the residual network becomes
What do we gain by being Bayesian?
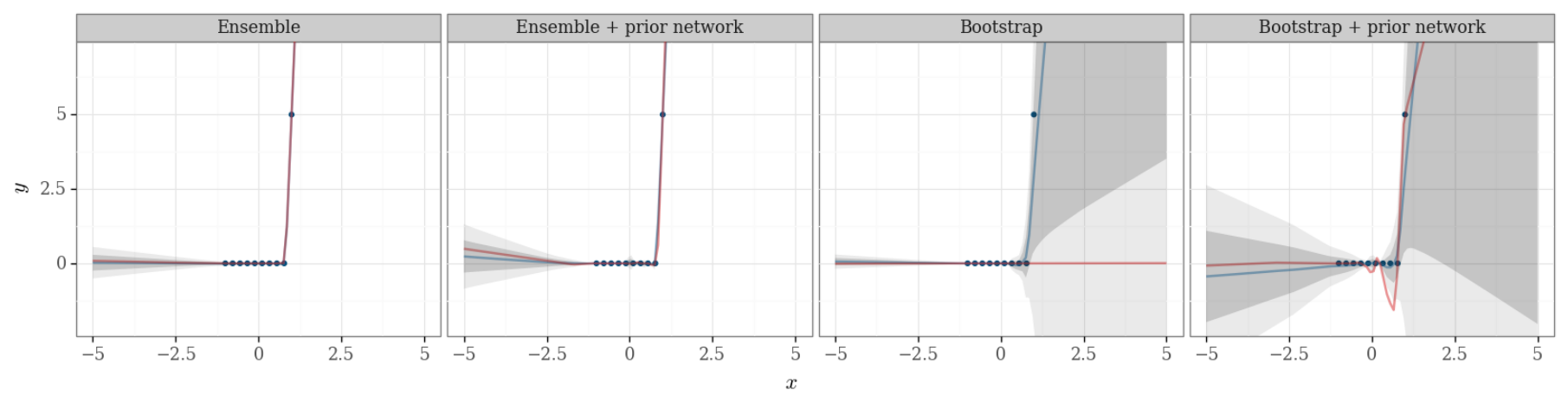
Osband et al. - Randomized prior functions for deep reinforcement learning (2018)
Better uncertainty measure!
Technical details
- PPO
- Online updates for RND
- Non-episodic returns for intrinsic rewards
- Separate value heads for extrinsic and intrinsic returns
- Clipping for extrinsic but not intrinsic rewards
- 2e9 total frames (before frame skip 4)
- Sticky actions with probability 25%
- CNN policy
Results
Consistently finds 22/24 rooms in Montezuma's Revenge.
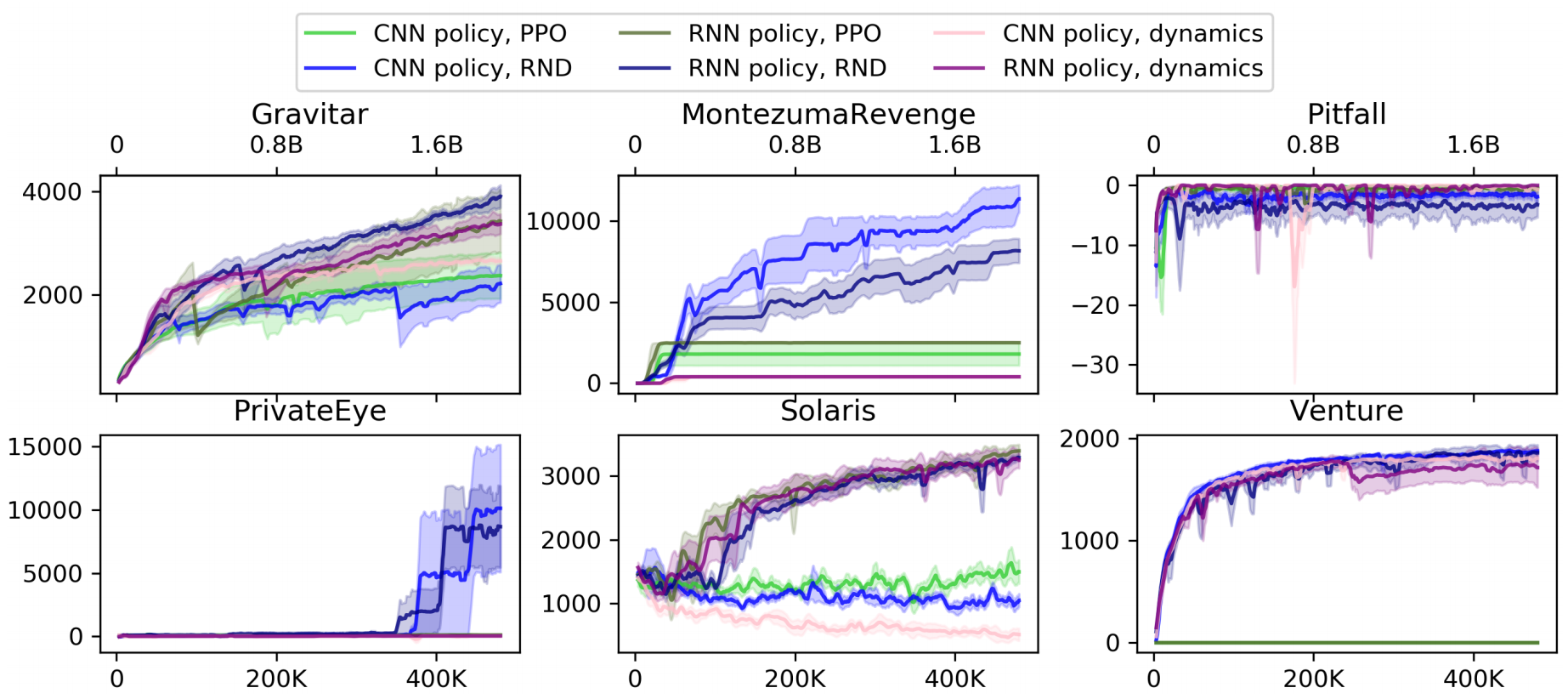
Results
Thank you
Speaker: Piotr Kozakowski
References:
Burda et al. - Exploration by random network distillation (2018)
Bellemare et al. - Unifying count-based exploration and intrinsic motivation (2016)
Stadie et al. - Incentivizing exploration in reinforcement learning with deep predictive models (2015)
Pathak et al. - Curiosity-driven exploration by self-supervised prediction (2017)
Fox et al. - Dora the explorer: Directed outreaching reinforcement action-selection (2018)
Osband et al. - Randomized prior functions for deep reinforcement learning (2018)
Exploration by Random Network Distillation
By Piotr Kozakowski
