Discrete Autoencoders
Gumbel-Softmax
vs
Improved Semantic Hashing
Piotr Kozakowski
Variational Autoencoders
\mathbb{E}_{x \sim D}[\mathbb{E}_{z \sim q(z|x)} [\log p(x|z)] - D_{KL} [q(z|x)~||~p(z)]]
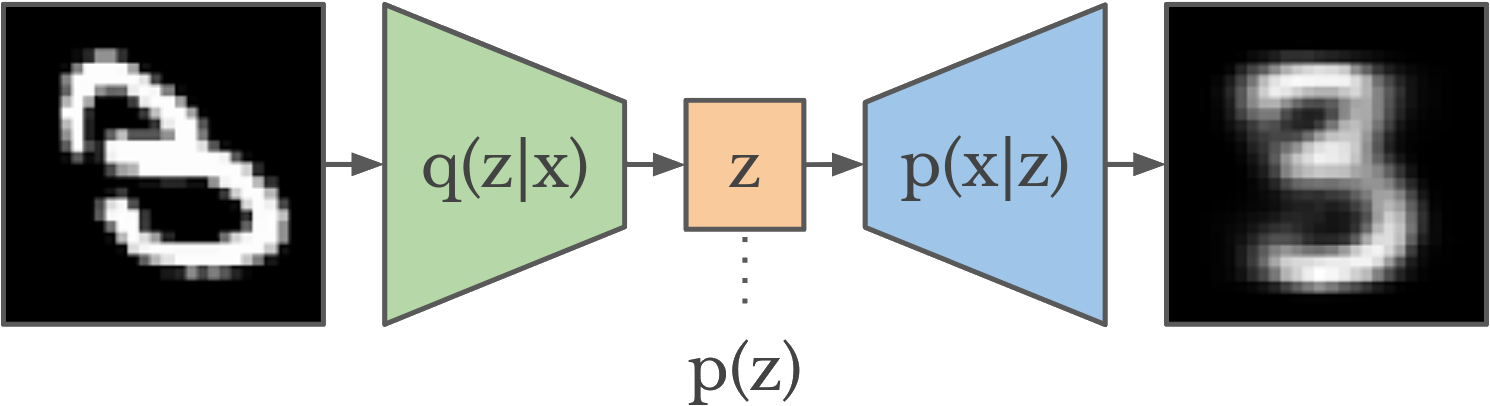
maximize
Variational Autoencoders
\mathbb{E}_{x \sim D}[\mathbb{E}_{z \sim q(z|x)} [\log p(x|z)] - D_{KL} [q(z|x)~||~p(z)]]
maximize
Training procedure:
- sample
- sample
- compute loss:
- backpropagate and update
x \sim D
z \sim q(z|x; \theta)
\log p(x|z; \theta) - D_{KL} [q(z|x; \theta)~||~p(z)]]
\theta
Variational Autoencoders
Training procedure:
- sample
- sample
- compute loss:
- backpropagate and update
x \sim D
z \sim q(z|x; \theta)
\log p(x|z; \theta) - D_{KL} [q(z|x; \theta)~||~p(z)]]
\theta
Commonly,
q(z|x) = \mathcal{N}(\mu(x), \sigma(x))
p(z) = \mathcal{N}(0, 1)
and
z \sim q(z|x; \theta)
How to backpropagate through
?
Reparametrization trick
Commonly,
q(z|x) = \mathcal{N}(\mu(x), \sigma(x))
p(z) = \mathcal{N}(0, 1)
and
z \sim q(z|x; \theta)
How to backpropagate through
?
Let
\epsilon \sim \mathcal{N}(0, 1)
and
z = \mu(x; \theta) + \epsilon \odot \sigma(x; \theta)
.
Backpropagate as usual, treating
\epsilon
as a constant.
Why Discrete?
- exactness
- better fit for some problems
- data compression
- easy lookup
Why Discrete in RL?
- learning combinatoric structures (e.g. approximate MDP - VaST)
- better fit for some problems (e.g. modeling stochasticity of the environment - SimPLe)
Corneil et al. - Efficient Model-Based Deep Reinforcement Learning with Variational State Tabulation (2018)
Kaiser et al. - Model-Based Reinforcement Learning for Atari (2019)
Gumbel-Softmax
Reparametrization trick for the categorical distribution:
Still can't backpropagate though.
g_i \sim \textrm{Gumbel}(0, 1)
z \sim \mathrm{Cat}(\pi)
z = \mathrm{argmax}_i(\log \pi_i + g_i)
generates a sample
with
g = -\log -\log u
with
u \sim \textrm{Uniform}(0, 1)
g \sim \mathrm{Gumbel}(0, 1)
generates a sample
Jang et al - Categorical Reparameterization with Gumbel-Softmax, 2016
Gumbel-Softmax
Approximate
g_i \sim \textrm{Gumbel}(0, 1)
\mathrm{GumbelSoftmax}(\pi) = \mathrm{softmax}_i((\log \pi_i + g_i)/\tau)
with
\mathrm{one\_hot}(\mathrm{argmax}_i \pi_i)
with
\mathrm{softmax}_i~\log \pi_i
\tau \rightarrow 0
Temperature annealing: as
,
\mathrm{GumbelSoftmax}(\pi) \rightarrow \mathrm{one\_hot}(\mathrm{argmax}_i \pi_i)
is differentiable - can backpropagate!
\mathrm{GumbelSoftmax}(\pi)
Jang et al - Categorical Reparameterization with Gumbel-Softmax, 2016
Gumbel-Softmax
Drop-in replacement for the normal distribution in VAE:
z = \mathrm{GumbelSoftmax(\pi(x))}
p(z) = \mathrm{Cat}(1/K, \dots, 1/K)
q(z|x) = \mathrm{Cat}(\pi(x))
Gumbel-Softmax
def sample_gumbel(shape, eps=1e-20):
u = torch.rand(shape)
return -torch.log(-torch.log(u + eps) + eps)
def gumbel_softmax(logits, temperature):
y = logits + sample_gumbel(logits.size())
return F.softmax(y / temperature, dim=-1)Gumbel-Softmax
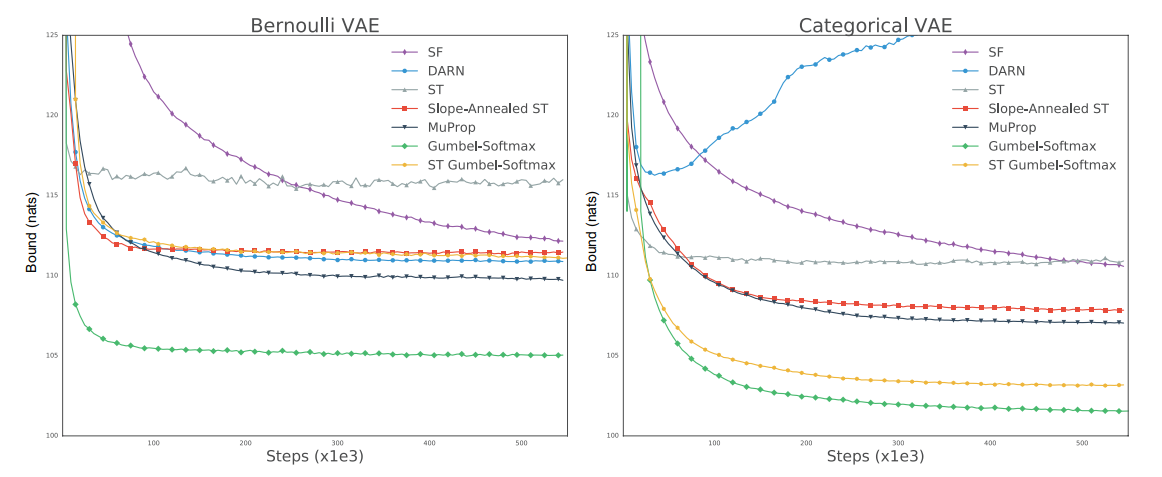
Improved Semantic Hashing
z = \mathrm{saturating\_sigmoid}(l(x) + \epsilon)
\mathrm{saturating\_sigmoid}(l) = \max(0, \min(1, \mathrm{sigmoid}(l) * 1.2 - 0.1))
Discretize
half of the time,
but backpropagate as if it was not discretized.
z
Binary latent variables.
with
\epsilon \sim \mathcal{N}(0, 1)
Noise forces
l(x)
to extreme values.
Kaiser et al - Discrete Autoencoders for Sequence Models, 2018
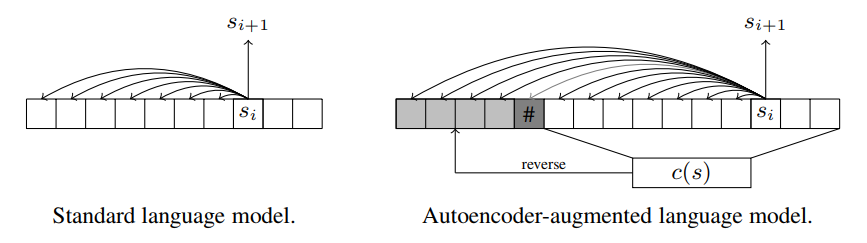
Improved Semantic Hashing
No probabilistic interpretation and no KL loss.
No prior to sample the latent from.
Solution: predict the latent autoregressively as a sequence of bits using an LSTM.
Predict several bits at a time.
Source: Tensor2Tensor
Improved Semantic Hashing
def saturating_sigmoid(logits):
return torch.clamp(
1.2 * torch.sigmoid(logits) - 0.1, min=0, max=1
)
def mix(a, b, prob=0.5):
mask = (torch.rand_like(a) < prob).float()
return mask * a + (1 - mask) * b
def improved_semantic_hashing(logits, noise_std=1):
noise = torch.normal(
mean=torch.zeros_like(logits), std=noise_std
)
noisy_logits = logits + noise
continuous = saturating_sigmoid(noisy_logits)
discrete = (
(noisy_logits > 0).float() +
continuous - continuous.detach()
)
return mix(continuous, discrete)Improved Semantic Hashing
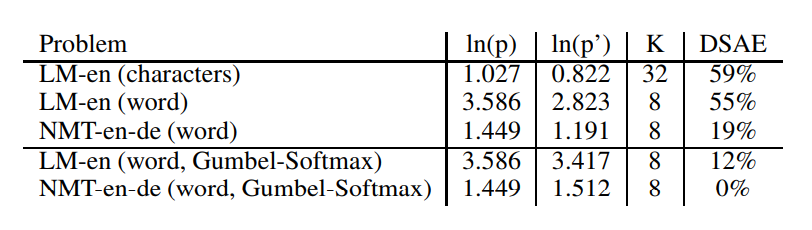
Improved Semantic Hashing
Theoretical comparison
Gumbel-softmax
- temperature annealing
- annealing rate needs tuning
- any categorical variables
- sampling from the prior
Improved semantic hashing
- stationary Gaussian noise
- robust to hyperparameters
- just binary variables
- no explicit way to sample
MNIST image reconstruction
Procedure:
- sample an image from MNIST
- encode
- discretize without noise
- decode
Metric: binary cross-entropy
MNIST image generation
Procedure:
- sample a discrete latent code
- decode
Metric: Inception score
\mathbb{E}_{x \sim p(x)}D_{KL}[q(y|x)~||~q(y)]
for a generator
and pretrained classifier
p(x)
q(y|x)
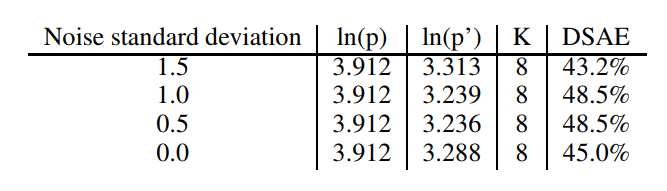
Reconstruction
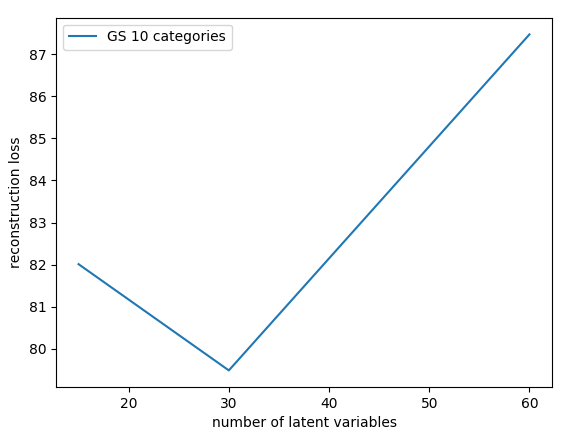
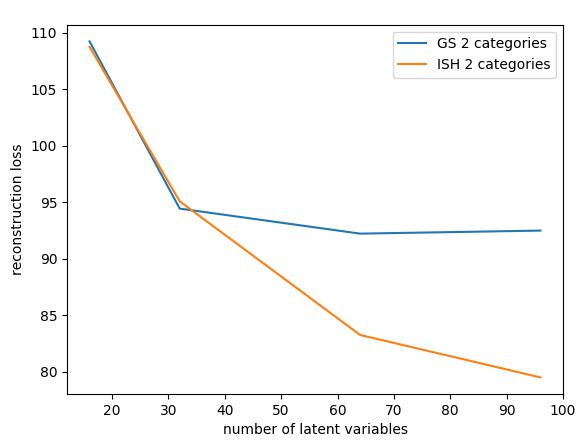
Reconstruction
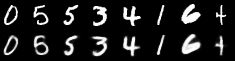
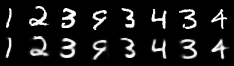
GS, 30 x 10
ISH, 96 x 2
Sampling
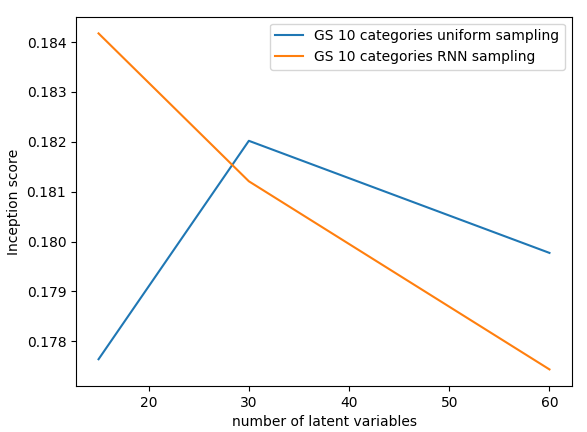
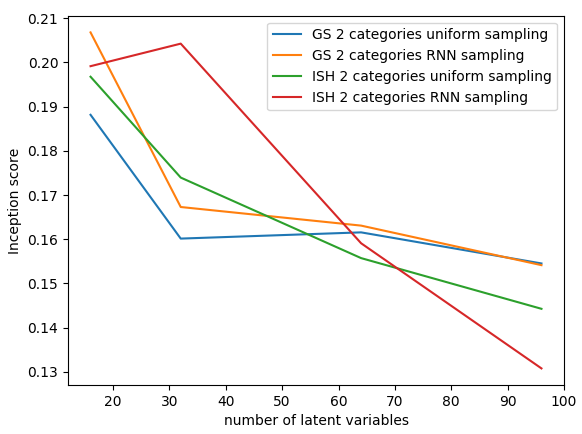
Sampling
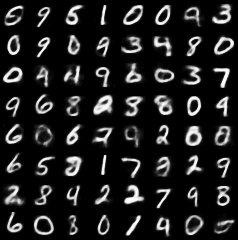
GS, 16 x 2
ISH, 32 x 2
Conclusions
- methods achieve comparable results
- GS is better at sampling
- ISH reconstruction scales much better with the number of variables
- GS is sensitive to the number of categories
- ISH has less hyperparameters to tune
- in both methods sampling is better with binary variables and RNN
Speaker:
Presentation:
Code:
References:
Jang et al. - Categorical Reparameterization with Gumbel-Softmax (2016)
Kaiser et al. - Discrete Autoencoders for Sequence Models (2018)
Corneil et al. - Efficient Model-Based Deep Reinforcement Learning with Variational State Tabulation (2018)
Kaiser et al. - Model-Based Reinforcement Learning for Atari (2019)
https://slides.com/piotrkozakowski/discrete-autoencoders
https://github.com/koz4k/gumbel-softmax-vs-discrete-ae
Piotr Kozakowski
Discrete Autoencoders
By Piotr Kozakowski
