Fast Differentiable Sorting and Ranking
ICML 2020
presented by Piotr Kozakowski
Sorting and ranking are important.
Sorting and ranking are important.
But not differentiable.
Sorting and ranking are important.
But not differentiable.
Sorting: piecewise linear - continuous, derivatives constant, zero or undefined.
Sorting and ranking are important.
But not differentiable.
Sorting: piecewise linear - continuous, derivatives constant, zero or undefined.
Ranking: piecewise constant - discontinuous, derivatives zero or undefined.
Goal: construct differentiable approximations of sorting and ranking.
Definitions
\theta \in \mathbb{R}^n~\text{- vector to sort}
\sigma(\theta) \in \Sigma~\text{- \textbf{argsort} of $\theta$, s.t. $\theta_{\sigma_1(\theta)} \geq ... \geq \theta_{\sigma_n(\theta)}$}
s(\theta) = \theta_{\sigma(\theta)} \in \mathbb{R}^n~\text{- \textbf{sort} of $\theta$}
r(\theta) = \sigma^{-1}(\theta) \in \Sigma~\text{- \textbf{rank} of $\theta$}
Example
\theta = (1.2, 0.1, 2.9)
\sigma(\theta) = (3, 1, 2)
s(\theta) = \theta_{\sigma(\theta)} = (2.9, 1.2, 0.1)
r(\theta) = \sigma^{-1}(\theta) = (2, 3, 1)
Discrete optimization formulations
s(\theta) = \mathrm{argmax}_{\sigma \in \Sigma} \langle \theta_\sigma, \rho \rangle \\
r(\theta) = \mathrm{argmax}_{\pi \in \Sigma} \langle \theta, \rho_\pi \rangle \\
\text{where}~\rho = (n, n - 1, ..., 1)
Permutahedron
\mathcal{P}(w) = \mathrm{conv}(w_\sigma : \sigma \in \Sigma)
Convex hull of permutations on w.
Permutahedron in 3d
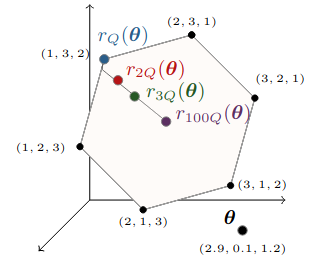
source: the paper
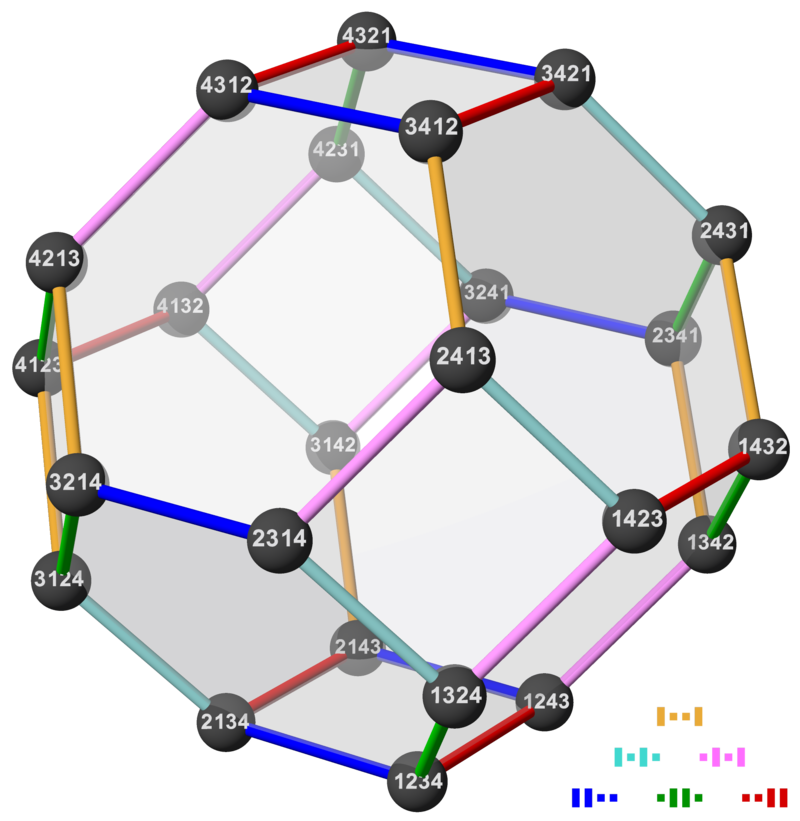
Permutahedron in 4d
source: Wikipedia
Linear programming formulations
s(\theta) = \mathrm{argmax}_{\sigma \in \Sigma} \langle \theta_\sigma, \rho \rangle \\
r(\theta) = \mathrm{argmax}_{\pi \in \Sigma} \langle \theta, \rho_\pi \rangle \\
\text{where}~\rho = (n, n - 1, ..., 1)
\Downarrow
s(\theta) = \mathrm{argmax}_{y \in \mathcal{P}(\theta)} \langle y, \rho \rangle \\
r(\theta) = \mathrm{argmax}_{\pi \in \mathcal{P}(\rho)} \langle y, -\theta \rangle \\
Linear programming formulations
s(\theta) = \mathrm{argmax}_{\sigma \in \Sigma} \langle \theta_\sigma, \rho \rangle \\
r(\theta) = \mathrm{argmax}_{\pi \in \Sigma} \langle \theta, \rho_\pi \rangle \\
\text{where}~\rho = (n, n - 1, ..., 1)
\Downarrow
s(\theta) = \mathrm{argmax}_{y \in \mathcal{P}(\theta)} \langle y, \rho \rangle \\
r(\theta) = \mathrm{argmax}_{\pi \in \mathcal{P}(\rho)} \langle y, -\theta \rangle \\
\}
same solutions
from the Fundamental Theorem of Linear Programming
Generalization
\text{where}~\rho = (n, n - 1, ..., 1)
\Downarrow
s(\theta) = \mathrm{argmax}_{y \in \mathcal{P}(\theta)} \langle y, \rho \rangle \\
r(\theta) = \mathrm{argmax}_{\pi \in \mathcal{P}(\rho)} \langle y, -\theta \rangle \\
P(z, w) = \mathrm{argmax}_{\mu \in \mathcal{P}(w)} \langle \mu, z \rangle \\
s(\theta) = P(\rho, \theta) \\
r(\theta) = P(-\theta, \rho)
Regularization
P(z, w) = \mathrm{argmax}_{\mu \in \mathcal{P}(w)} \langle \mu, z \rangle
\Downarrow
P_Q(z, w) = \mathrm{argmax}_{\mu \in \mathcal{P}(w)} \langle \mu, z \rangle - ||z||^2
Regularization
P(z, w) = \mathrm{argmax}_{\mu \in \mathcal{P}(w)} \langle \mu, z \rangle
\Downarrow
P_Q(z, w) = \mathrm{argmax}_{\mu \in \mathcal{P}(w)} \langle \mu, z \rangle - ||z||^2
= \mathrm{argmin}_{\mu \in \mathcal{P}(w)} ||\mu - z||^2
Regularization
P(z, w) = \mathrm{argmax}_{\mu \in \mathcal{P}(w)} \langle \mu, z \rangle
\Downarrow
P_Q(z, w) = \mathrm{argmax}_{\mu \in \mathcal{P}(w)} \langle \mu, z \rangle - ||z||^2
= \mathrm{argmin}_{\mu \in \mathcal{P}(w)} ||\mu - z||^2
Euclidean projection of z onto the permutahedron!
\}
Regularization
P_{\epsilon Q}(z, w) = \mathrm{argmax}_{\mu \in \mathcal{P}(w)} \langle \mu, z \rangle - \epsilon ||z||^2
= \mathrm{argmin}_{\mu \in \mathcal{P}(w)} ||\mu - z/\epsilon||^2
\epsilon~\text{- regularization strength}
Regularization
P_{\epsilon E}(z, w) = \log \mathrm{argmax}_{\mu \in \mathcal{P}(e^w)} \langle \mu, z \rangle - \epsilon \langle \mu, \log \mu - 1 \rangle
(not going to talk about that)
How does it work?
r_{\epsilon Q}(\theta) = P_{\epsilon Q}(-\theta, \rho) = \mathrm{argmin}_{\mu \in \mathcal{P}(\rho)} ||\mu - (-\theta)/\epsilon||^2 \\
\rho = (3, 2, 1)
Properties
Effect of regularization strength
\theta = (0, 3, 1, 2) \\
s(\theta) = (3, 2, 1, 0) \\
r(\theta) = (4, 1, 3, 2)
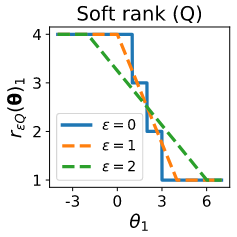
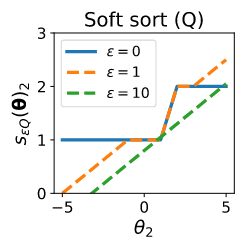
Reduction to isotonic regression
TLDR: we can pose the problem as isotonic regression
and solve it in O(n log n) time and O(n) space.
And we can multiply with the Jacobian in O(n).
(it's sparse)
Experiment: top-1 classification on CIFAR
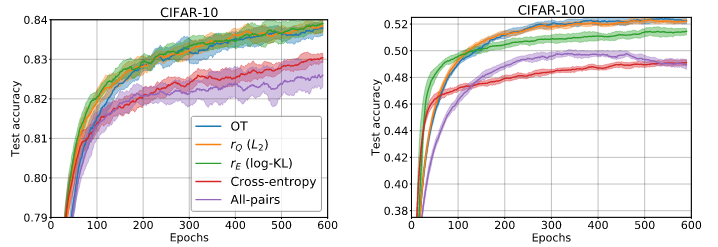
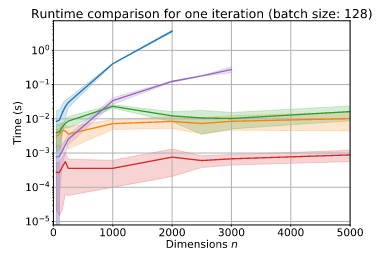
Experiment: robust regression
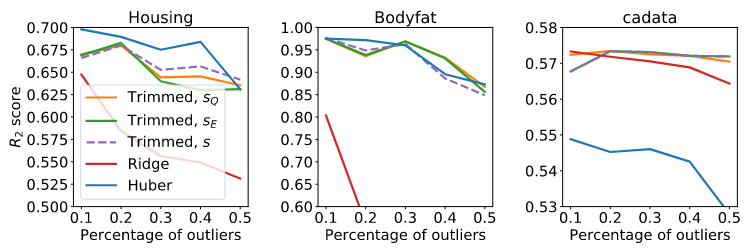
Idea: sort the losses and ignore the top k of them.
Serif
By Piotr Kozakowski
