Mathematics

Back to school level Maths :)

Maths Basics-I

• Prime Numbers
• Divisors
• Prime Factorisation 

Prime Numbers

Divisors?

Prime Factorisation?

Maths Basics-II

• GCD
• Euclid's Algorithm
• LCM
• GCD of N Numbers

GCD Brute Force

Euclid's Algorithm

GCD's of N Numbers

LCM Brute Force

LCM using GCD

Trailing Zeroes | Warmup

Maths Basics

• Fibonacci Series
• Arithmetic Progression
• Geometric Progression

Fibonacci Number

Write a program to compute the nth Fibonacci Number.
Fibonacci Series:

0, 1, 1, 2, 3, 5, 8 , ........

Arithmetic Progression

An arithmetic progression (AP) is a sequence where the differences between every two consecutive terms are the same.

Arithmetic Progression

An arithmetic progression (AP) is a sequence where the differences between every two consecutive terms are the same.

For example, 1, 5, 9, 13, 17, 21, 25, 29, 33, ...

a = 1 (the first term)
d = 4 (the "common difference" between terms)

AP Nth Term

For example, 1, 5, 9, 13, 17, 21, 25, 29, 33, ...

a = 1 (the first term)
d = 4 (the "common difference" between terms)

an = a + (n-1)d

Nth term of an AP

Geometric Progression

A geometric progression is a progression where every term bears a constant ratio to its preceding term.

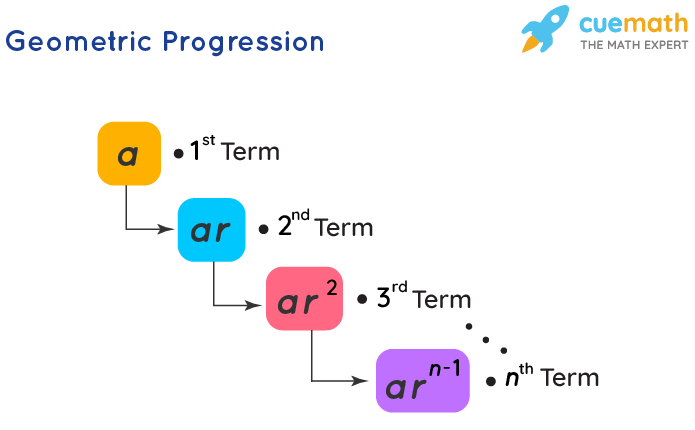
GP Nth Term

Text

Maths Basics-IV 

• Binomial Coefficients
• Permutation
• Combination

Combinatorics

Combinatorics is all about number of ways of choosing some objects out of a collection and/or number of ways of their arrangement.

Real Example

For example suppose there are five members in a club, let's say there names are A, B, C, D, and E, and one of them is to be chosen as the coordinator.

Clearly any one out of them can be chosen so there are 5 ways. Now suppose two members are to be chosen for the position of coordinator and co-coordinator. What is the number of ways to choose the two?

Permutation

Let's generalize it. Permutations of choosing R distinct objects out of a collection of N objects can be calculated using the following formula:

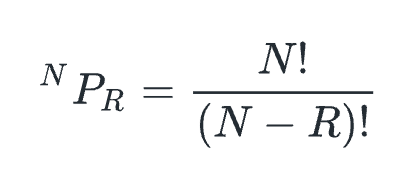
Combination

Combinations of choosing R distinct objects out of a collection of N objects can be calculated using the following formula

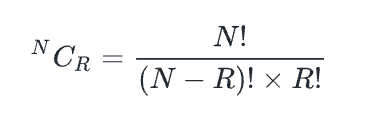
Basic Combinatorics Rules:

Suppose there are two sets A and B with finite elements.

1. The Rule of Product
   The product rule states that if there are X number of ways to choose one element from A and Y number of ways to choose one element from B, then there will be X×Y number of ways to choose two elements, one from A and one from B.

2. The Rule of Sum
   The sum rule states that if there are X number of ways to choose one element from A and Y number of ways to choose one element from B, then there will be X+Y number of ways to choose one element that can belong to either A or to B.

Binomial Coefficient 👨‍💻

Choosing 3 Cats out of 5 Cats?

Maths Basics-V 

• Logarithm