Applying Binary Search
Prateek Narang


Binary Search Application

What you will learn?
- Monotonic Search Spaces
-
Binary Search Application
-
Aggressive Cows - Concept, Code, Complexity



Binary Search is a POWERFUL Technique! 💪
It can be used a variety of problems!


0 1 2 3 4 5 6 7 8

We have seen Binary Search can be used for searching in a sorted array!
1 3 4 5 9 12 22 38 45


-
It can be applied for searching in monotonic search spaces as well!

Monotonic Function? 🧐

Monotonic Function
Non-increasing fn
Non-decreasing fn
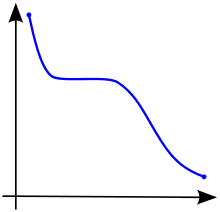
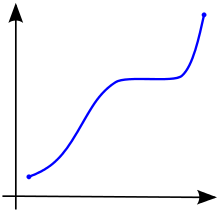

Sorted Array also represents
Monotonic Search Space Search
1 3 4 5 9 12 22 38 45
0 1 2 3 4 5 6 7 8


Farmer John has built a new long farm, with N stalls. The stalls are located along a straight line at positions x1,...,xN.
🐮 Aggressive Cows
x1 x2 x3 x4 x5






His C (2 <= C <= N) cows don't like this barn layout and become aggressive towards each other once put into a stall. To prevent the cows from hurting each other, Farmer wants to assign the cows to the stalls, such that the minimum distance between any two of them is as large as possible. What is the largest minimum distance?
🐮 Aggressive Cows
x1 x2 x3 x4 x5






🐮 Aggressive Cows
N = 5 Stalls
Stalls = [1,4, 8, 2 9]
C = 3 Cows
🐮🐮🐮



x=8


x=9
x=1

x=2

x=4


🐮 Aggressive Cows
Goal : Place C cows in N stalls so that
min difference between two cows is maximum.



x=8


x=9
x=1

x=2

x=4

🐮
🐮
🐮

🐮 Aggressive Cows
Possible Scenario #1
🐮
x=8


x=9
x=1

x=2

x=4

🐮
🐮

🐮 Aggressive Cows
Possible Scenario #1
🐮
x=8


x=9
x=1

x=2

x=4

🐮
🐮

🐮 Aggressive Cows
Possible Scenario #1
🐮
x=8


x=9
x=1

x=2

x=4

🐮
🐮

🐮 Aggressive Cows
Possible Scenario #1
🐮
x=8


x=9
x=1

x=2

x=4

🐮
🐮
1 unit
2 unit
sep = min(1,2) = 1

🐮 Aggressive Cows
Possible Scenario #2
🐮
x=8


x=9
x=1

x=2

x=4

🐮
🐮

🐮 Aggressive Cows
Possible Scenario #2
🐮
x=8


x=9
x=1

x=2

x=4

🐮
🐮

🐮 Aggressive Cows
Possible Scenario #2
🐮
x=8


x=9
x=1

x=2

x=4

🐮
🐮

🐮 Aggressive Cows
Possible Scenario #2
🐮
x=8


x=9
x=1

x=2

x=4

🐮
🐮
2 unit
5 units
sep = min(2,5) = 2

🐮 Aggressive Cows
Possible Scenario #3
🐮
x=8


x=9
x=1

x=2

x=4

🐮
🐮

🐮 Aggressive Cows
Possible Scenario #3
🐮
x=8


x=9
x=1

x=2

x=4

🐮
🐮

🐮 Aggressive Cows
Possible Scenario #3
🐮
x=8


x=9
x=1

x=2

x=4

🐮
🐮

🐮 Aggressive Cows
Possible Scenario #3
🐮
x=8


x=9
x=1

x=2

x=4

🐮
🐮
3 unit
4 unit
ans = min(3,4) = 3


Final Ans ?
Scenario #1 min_sep = 1
Scenario #2 min_sep = 2
Scenerio #3 min_sep = 3
.
.
.
Find the maximum of min separation!


Final Ans ?
Scenario #1 min_sep = 1
Scenario #2 min_sep = 2
Scenerio #3 min_sep = 3
.
.
.
Find the maximum of min separation!

But how we do solve it optimally? 👨💻

Let's Binary Search!

Find out the search space!
The search space is the range in which your answer can possibly lie.
🚀 What you need to know?

🐮 Search Space in Aggressive Cows
Goal : Place C cows in N stalls so that
min difference between two cows is maximum.
🐮🐮🐮



x=8


x=9
x=1

x=2

x=4

Search Space : Distance between cows!

🐮 Search Space in Aggressive Cows
Min Distance : ___
🐮
x=8


x=9
x=1

x=2

x=4

🐮

🐮 Search Space in Aggressive Cows
Min Distance : 0
🐮
x=8


x=9
x=1

x=2

x=4

🐮

🐮 Search Space
Max Distance :
Last Stall - First Stall
(Note: after Sorting according to coordinates)
= 9 - 1
= 8
🐮
x=8


x=9
x=1

x=2

x=4

🐮


🐮 Search Space
🐮
x=8


x=9
x=1

x=2

x=4

🐮
0 1 2 3 4 5 6 7 8
Distance
Stalls

🐮 Binary Search
x=8


x=9
x=1

x=2

x=4

0 1 2 3 4 5 6 7 8
Distance
Stalls
s
e

🐮 Binary Search
x=8


x=9
x=1

x=2

x=4

0 1 2 3 4 5 6 7 8
Distance
Stalls
mid
s
e

🐮 Binary Search
x=8


x=9
x=1

x=2

x=4

0 1 2 3 4 5 6 7 8
Distance
Stalls
mid = 4
e
s

🐮 Check
x=8


x=9
x=1

x=2

x=4

Distance = 4
Stalls
🐮
Cows Placed = 1

🐮 Check
x=8


x=9
x=1

x=2

x=4

Distance = 4
Stalls
🐮
🐮
Cows Placed = 1

🐮 Check
x=8


x=9
x=1

x=2

x=4

Distance = 4
Stalls
🐮
🐮
🐮
Cows Placed = 1

🐮 Check
x=8


x=9
x=1

x=2

x=4

Distance = 4
Stalls
🐮
🐮
🐮
Cows Placed = 2

🐮 Check
x=8


x=9
x=1

x=2

x=4

Distance = 4
Stalls
🐮
🐮
🐮
Cows Placed = 2
🐮

🐮 Check
x=8


x=9
x=1

x=2

x=4

Distance = 4
Stalls
🐮
🐮
🐮
Cows Placed = 2
🐮
Hence, we could place only two cows! 😔
Clearly 4 is not the answer, go left in search space!

🐮 Binary Search
x=8


x=9
x=1

x=2

x=4

0 1 2 3 4 5 6 7 8
Distance
Stalls
mid = 4
s
e

🐮 Binary Search
x=8


x=9
x=1

x=2

x=4

0 1 2 3 4 5 6 7 8
Distance
Stalls
e = mid - 1
s
e

🐮 Binary Search
x=8


x=9
x=1

x=2

x=4

0 1 2 3 4 5 6 7 8
Distance
Stalls
s
e
mid

🐮 Binary Search
x=8


x=9
x=1

x=2

x=4

0 1 2 3 4 5 6 7 8
Distance
Stalls
s
e
mid

🐮 Check
x=8


x=9
x=1

x=2

x=4

Distance = 1
Stalls
🐮
Cows Placed = 1

🐮 Check
x=8


x=9
x=1

x=2

x=4

Distance = 1
Stalls
🐮
Cows Placed = 2
🐮

🐮 Check
x=8


x=9
x=1

x=2

x=4

Distance = 1
Stalls
🐮
Cows Placed = 3
🐮
🐮

🐮 Check
x=8


x=9
x=1

x=2

x=4

Distance = 1
Stalls
🐮
Cows Placed = 3
🐮
🐮
Hence, as all cows are placed 😁 we stop and assume 1 as our current ans.

🐮 Binary Search
x=8


x=9
x=1

x=2

x=4

0 1 2 3 4 5 6 7 8
Distance
Stalls
s
e
mid
current_ans = 1

🐮 Binary Search
x=8


x=9
x=1

x=2

x=4

0 1 2 3 4 5 6 7 8
Distance
Stalls
s
e
mid
s = mid + 1
current_ans = 1

🐮 Binary Search
x=8


x=9
x=1

x=2

x=4

0 1 2 3 4 5 6 7 8
Distance
Stalls
s
e

🐮 Binary Search
x=8


x=9
x=1

x=2

x=4

0 1 2 3 4 5 6 7 8
Distance
Stalls
s
e
mid

🐮 Binary Search
x=8


x=9
x=1

x=2

x=4

0 1 2 3 4 5 6 7 8
Distance
Stalls
s
e
mid

🐮 Check
x=8


x=9
x=1

x=2

x=4

Distance = 2
Stalls
🐮
Cows Placed = 1

🐮 Check
x=8


x=9
x=1

x=2

x=4

Distance = 2
Stalls
🐮
Cows Placed = 1
🐮

🐮 Check
x=8


x=9
x=1

x=2

x=4

Distance = 2
Stalls
🐮
Cows Placed = 2
🐮

🐮 Check
x=8


x=9
x=1

x=2

x=4

Distance = 2
Stalls
🐮
Cows Placed = 3
🐮
🐮

🐮 Check
x=8


x=9
x=1

x=2

x=4

Distance = 2
Stalls
🐮
Cows Placed = 3
🐮
🐮
Hence, as all cows are placed 😁 we stop and update 2 as our current ans.

🐮 Binary Search
x=8


x=9
x=1

x=2

x=4

0 1 2 3 4 5 6 7 8
Distance
Stalls
s
e
mid
s = mid + 1
current_ans = 2

🐮 Binary Search
x=8


x=9
x=1

x=2

x=4

0 1 2 3 4 5 6 7 8
Distance
Stalls
s
e

🐮 Binary Search
x=8


x=9
x=1

x=2

x=4

0 1 2 3 4 5 6 7 8
Distance
Stalls
s
e
mid

🐮 Binary Search
x=8


x=9
x=1

x=2

x=4

0 1 2 3 4 5 6 7 8
Distance
Stalls
s
e
mid

🐮 Check
x=8


x=9
x=1

x=2

x=4

Distance = 3
Stalls
🐮
Cows Placed = 1

🐮 Check
x=8


x=9
x=1

x=2

x=4

Distance = 3
Stalls
🐮
Cows Placed = 1
🐮

🐮 Check
x=8


x=9
x=1

x=2

x=4

Distance = 3
Stalls
🐮
Cows Placed = 1
🐮

🐮 Check
x=8


x=9
x=1

x=2

x=4

Distance = 3
Stalls
🐮
Cows Placed = 2
🐮

🐮 Check
x=8


x=9
x=1

x=2

x=4

Distance = 3
Stalls
🐮
Cows Placed = 3
🐮
🐮

🐮 Check
x=8


x=9
x=1

x=2

x=4

Distance = 3
Stalls
🐮
Cows Placed = 3
🐮
🐮
Hence, as all cows are placed 😁 we stop and update 3 as our current ans.

🐮 Binary Search
x=8


x=9
x=1

x=2

x=4

0 1 2 3 4 5 6 7 8
Distance
Stalls
s
e
mid
s = mid + 1
current_ans = 3

🐮 Binary Search
x=8


x=9
x=1

x=2

x=4

0 1 2 3 4 5 6 7 8
Distance
Stalls
s
e
mid
s > e 🧐
current_ans = 3

🐮 Binary Search
x=8


x=9
x=1

x=2

x=4

0 1 2 3 4 5 6 7 8
Distance
Stalls
s
e
mid
STOP
current_ans = 3

🐮 Binary Search
x=8


x=9
x=1

x=2

x=4

0 1 2 3 4 5 6 7 8
Distance
Stalls
s
e
mid
ans = 3
current_ans = 3

Monotonic Search Space
0 1 2 3 4 5 6 7 8
Distance
0 1 2 3 4 5 6 7 8
f
1
0
ans = 3

Binary Search is an algorithm that can be used to search an element in a sorted dataset monotonic search space.
Search space depends upon the value to be searched.
Depending upon the problem statement we might be optimising for a quantity such time, distance, cost etc.
So binary search can be applied in all many optimisation problems of the min( max (....) ) or max(min(...) ) given the problem has a monotonic search space!
🚀 Binary Search


Code 👨💻


private static int binarySearch(int[] stalls, int C) {
}

private static int binarySearch(int[] stalls, int C) {
int n = stalls.length;
Arrays.sort(stalls);
int s = 0;
int e = stalls[n-1] - stalls[0];
}

private static int binarySearch(int[] stalls, int C) {
int n = stalls.length;
Arrays.sort(stalls);
int s = 0;
int e = stalls[n-1] - stalls[0];
int current_ans;
while(s<=e){
int mid = (s+e)/2;
}
return current_ans;
}

private static int binarySearch(int[] stalls, int C) {
int n = stalls.length;
Arrays.sort(stalls);
int s = 0;
int e = stalls[n-1] - stalls[0];
int current_ans;
while(s<=e){
int mid = (s+e)/2;
if(canPlace(stalls,mid,C)){
current_ans = mid;
s = mid + 1;
}
}
return current_ans;
}

private static int binarySearch(int[] stalls, int C) {
int n = stalls.length;
Arrays.sort(stalls);
int s = 0;
int e = stalls[n-1] - stalls[0];
int current_ans;
while(s<=e){
int mid = (s+e)/2;
if(canPlace(stalls,mid,C)){
current_ans = mid;
s = mid + 1;
}
else{
e = mid - 1;
}
}
}

private static int binarySearch(int[] stalls, int C) {
int n = stalls.length;
Arrays.sort(stalls);
int s = 0;
int e = stalls[n-1] - stalls[0];
int current_ans;
while(s<=e){
int mid = (s+e)/2;
if(canPlace(stalls,mid,C)){
current_ans = mid;
s = mid + 1;
}
else{
e = mid - 1;
}
}
return current_ans;
}

private static int binarySearch(int[] stalls, int C) {
int n = stalls.length;
Arrays.sort(stalls);
int s = 0;
int e = stalls[n-1] - stalls[0];
int current_ans;
while(s<=e){
int mid = (s+e)/2;
if(canPlace(stalls,mid,C)){
current_ans = mid;
s = mid + 1;
}
else{
e = mid - 1;
}
}
return current_ans;
}

private boolean canPlace(int[] stalls, int minSep, int C){
int cows=1;
int lastCowX = stalls[0];
}
private static int binarySearch(int[] stalls, int C) {
int n = stalls.length;
Arrays.sort(stalls);
int s = 0;
int e = stalls[n-1] - stalls[0];
int current_ans;
while(s<=e){
int mid = (s+e)/2;
if(canPlace(stalls,mid,C)){
current_ans = mid;
s = mid + 1;
}
else{
e = mid - 1;
}
}
return current_ans;
}

private boolean canPlace(int[] stalls, int minSep, int C){
int cows=1;
int lastCowX = stalls[0];
for(int i=1; i<stalls.size(); i++){
//place a cow if dist of current stall - prev >= threshold
}
}
private static int binarySearch(int[] stalls, int C) {
int n = stalls.length;
Arrays.sort(stalls);
int s = 0;
int e = stalls[n-1] - stalls[0];
int current_ans;
while(s<=e){
int mid = (s+e)/2;
if(canPlace(stalls,mid,C)){
current_ans = mid;
s = mid + 1;
}
else{
e = mid - 1;
}
}
return current_ans;
}

private boolean canPlace(int[] stalls, int minSep, int C){
int cows=1;
int lastCowX = stalls[0];
for(int i=1; i<stalls.size(); i++){
//place a cow if dist of current stall - prev >= threshold
if(stalls[i] - lastCowX >= minDist){
cows++;
lastCowX = stalls[i];
}
}
}
private static int binarySearch(int[] stalls, int C) {
int n = stalls.length;
Arrays.sort(stalls);
int s = 0;
int e = stalls[n-1] - stalls[0];
int current_ans;
while(s<=e){
int mid = (s+e)/2;
if(canPlace(stalls,mid,C)){
current_ans = mid;
s = mid + 1;
}
else{
e = mid - 1;
}
}
return current_ans;
}

private boolean canPlace(int[] stalls, int minSep, int C){
int cows=1;
int lastCowX = stalls[0];
for(int i=1; i<stalls.size(); i++){
//place a cow if dist of current stall - prev >= threshold
if(stalls[i] - lastCowX >= minDist){
cows++;
lastCowX = stalls[i];
if(cows==C){
return true;
}
}
}
}
private static int binarySearch(int[] stalls, int C) {
int n = stalls.length;
Arrays.sort(stalls);
int s = 0;
int e = stalls[n-1] - stalls[0];
int current_ans;
while(s<=e){
int mid = (s+e)/2;
if(canPlace(stalls,mid,C)){
current_ans = mid;
s = mid + 1;
}
else{
e = mid - 1;
}
}
return current_ans;
}

private boolean canPlace(int[] stalls, int minSep, int C){
int cows=1;
int lastCowX = stalls[0];
for(int i=1; i<stalls.size(); i++){
//place a cow if dist of current stall - prev >= threshold
if(stalls[i] - lastCowX >= minDist){
cows++;
lastCowX = stalls[i];
if(cows==C){
return true;
}
}
}
return false;
}
private static int binarySearch(int[] stalls, int C) {
int n = stalls.length;
Arrays.sort(stalls);
int s = 0;
int e = stalls[n-1] - stalls[0];
int current_ans;
while(s<=e){
int mid = (s+e)/2;
if(canPlace(stalls,mid,C)){
current_ans = mid;
s = mid + 1;
}
else{
e = mid - 1;
}
}
return current_ans;
}

Let's discuss space and time
Complexity Analysis



Time? 👨💻


private static int binarySearch(int[] stalls, int C) {
int n = stalls.length;
Arrays.sort(stalls);
int s = 0;
int e = stalls[n-1] - stalls[0];
int current_ans;
while(s<=e){
int mid = (s+e)/2;
if(canPlace(stalls,mid,C)){
current_ans = mid;
s = mid + 1;
}
else{
e = mid - 1;
}
}
return current_ans;
}

private boolean canPlace(int[] stalls, int minSep, int C){
int cows=1;
int lastCowX = stalls[0];
for(int i=1; i<stalls.size(); i++){
//place a cow if dist of current stall - prev >= threshold
if(stalls[i] - lastCowX >= minDist){
cows++;
lastCowX = stalls[i];
if(cows==C){
return true;
}
}
}
return false;
}
private static int binarySearch(int[] stalls, int C) {
int n = stalls.length;
Arrays.sort(stalls);
int s = 0;
int e = stalls[n-1] - stalls[0];
int current_ans;
while(s<=e){
int mid = (s+e)/2;
if(canPlace(stalls,mid,C)){
current_ans = mid;
s = mid + 1;
}
else{
e = mid - 1;
}
}
return current_ans;
}

Space? 👨💻


private boolean canPlace(int[] stalls, int minSep, int C){
int cows=1;
int lastCowX = stalls[0];
for(int i=1; i<stalls.size(); i++){
//place a cow if dist of current stall - prev >= threshold
if(stalls[i] - lastCowX >= minDist){
cows++;
lastCowX = stalls[i];
if(cows==C){
return true;
}
}
}
return false;
}
private static int binarySearch(int[] stalls, int C) {
int n = stalls.length;
Arrays.sort(stalls);
int s = 0;
int e = stalls[n-1] - stalls[0];
int current_ans;
while(s<=e){
int mid = (s+e)/2;
if(canPlace(stalls,mid,C)){
current_ans = mid;
s = mid + 1;
}
else{
e = mid - 1;
}
}
return current_ans;
}

Thank you! 👨💻
[Scaler] Aggressive Cows
By Prateek Narang
[Scaler] Aggressive Cows
- 323



