1.10 Vectors and Matrices
What are they and why to we care about them ?

Vectors
What are they ?
(c) One Fourth Labs

- Magnitude of a vector
- Direction of a vector
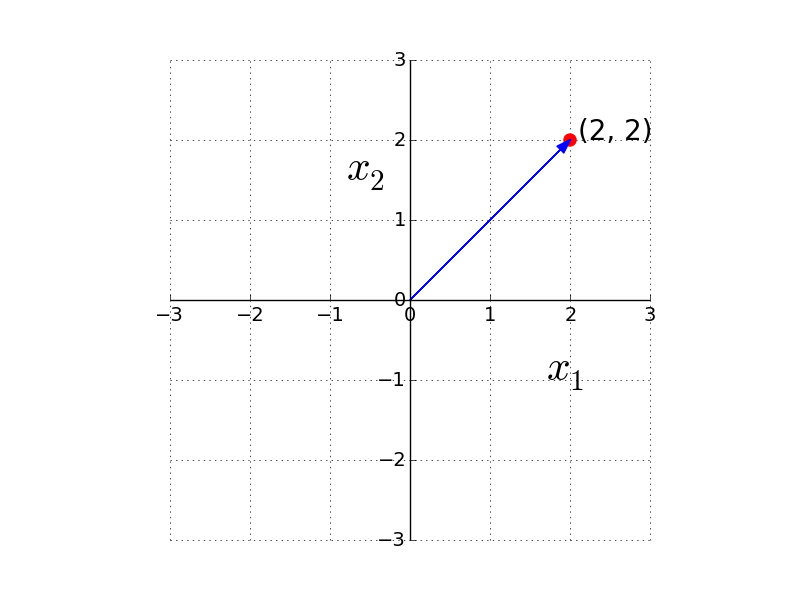
Magnitude of a vector
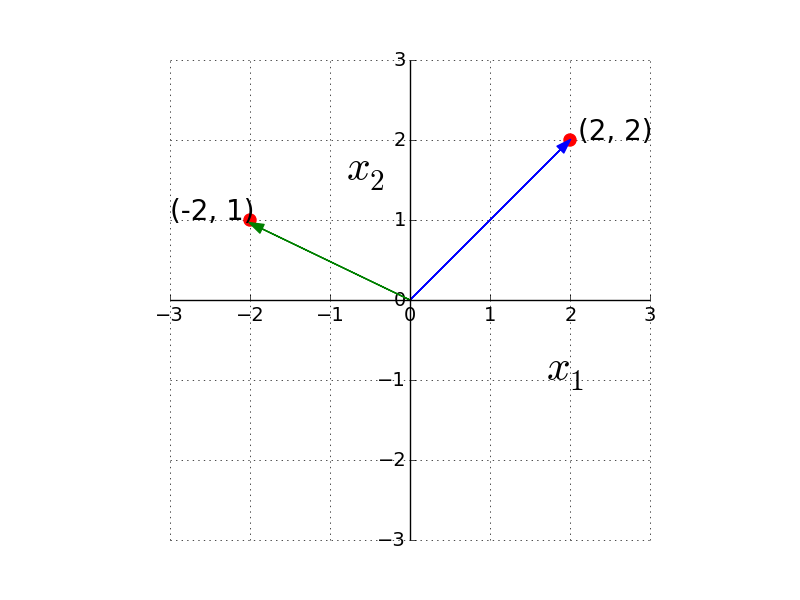
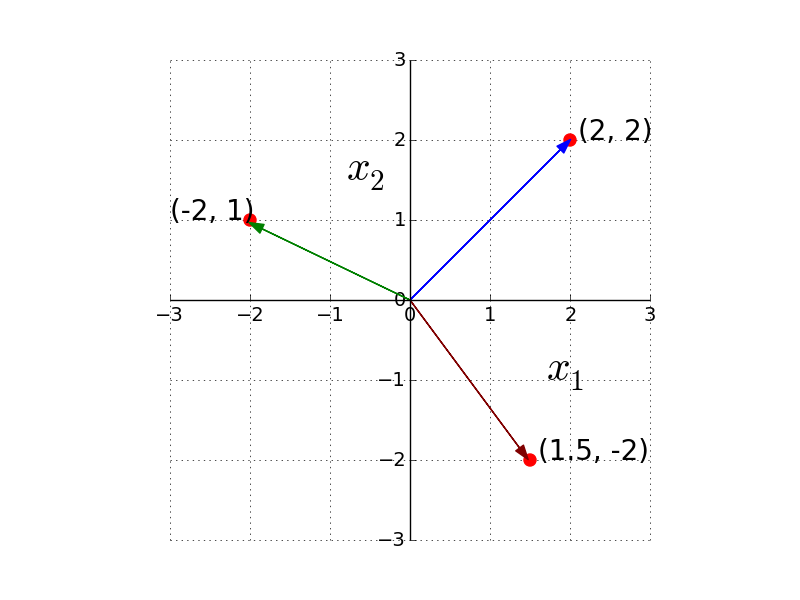
Magnitude of (2,2)
Magnitude of (-2,1)
Magnitude of (1.5,-2)
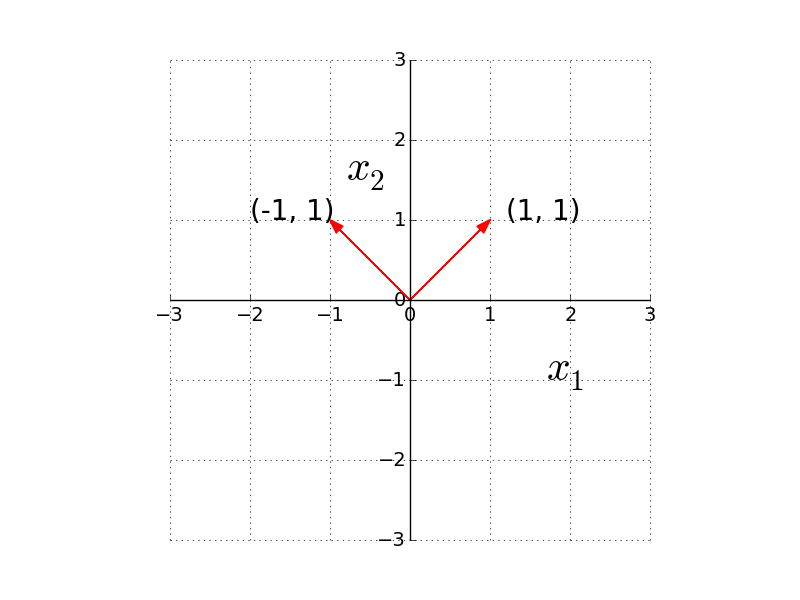
Magnitude of (1,1)
Magnitude of (-1,1)
Vectors
What are they ? (some jargon)
(c) One Fourth Labs

Euclidean Space
In geometry, a two- or three-dimensional space in which the axioms and postulates of Euclidean geometry apply is a Euclidean space. A space in any finite number of dimensions, in which points are designated by coordinates (one for each dimension) and the distance between two points is given by a distance formula.
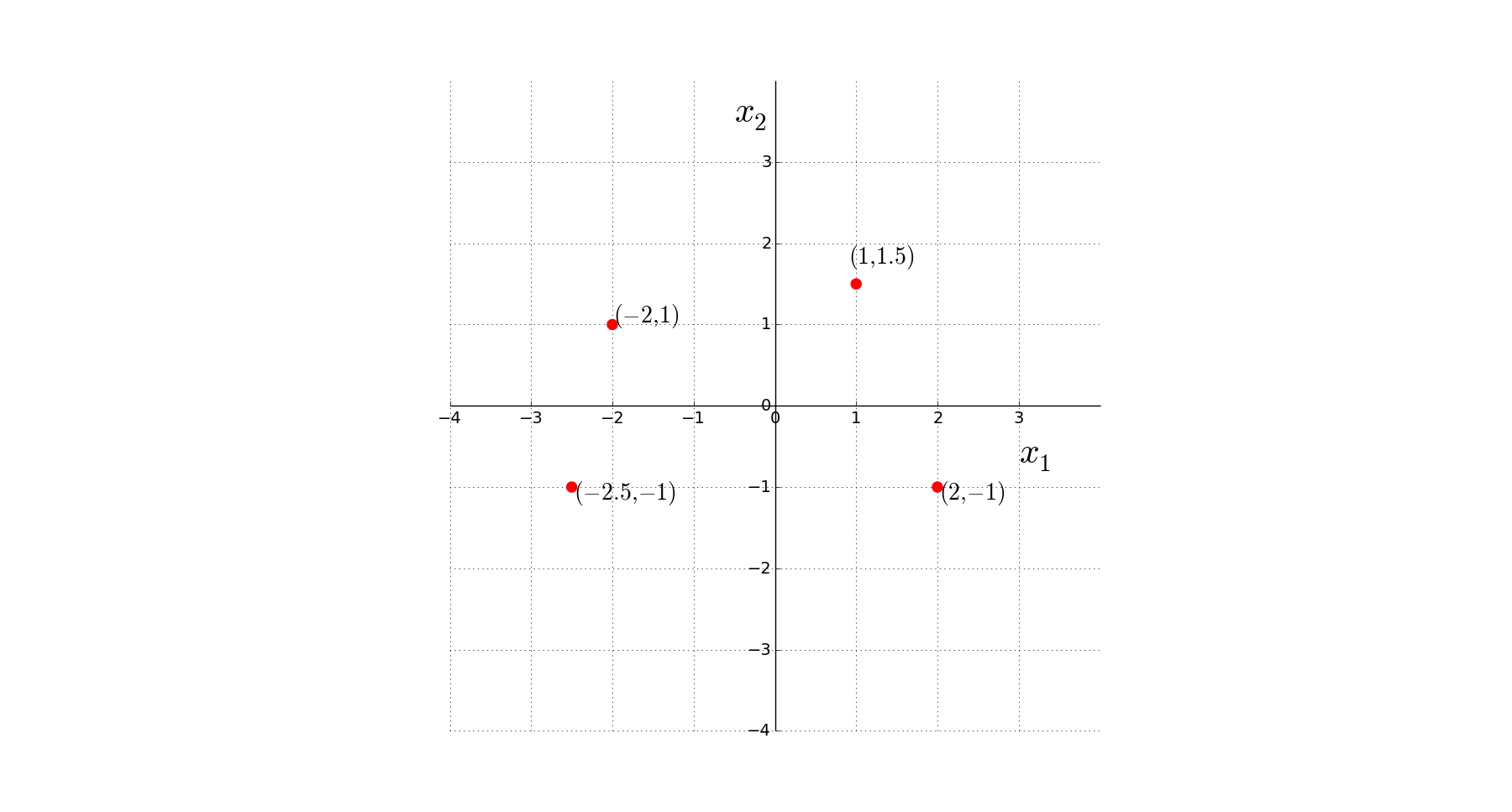
2D Euclidean Space
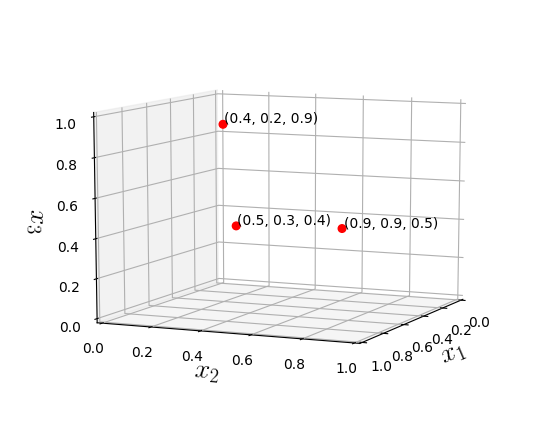
3D Euclidean Space
In geometry, a two- or three-dimensional space in which the axioms and postulates of Euclidean geometry apply is a Euclidean space. A space in any finite number of dimensions, in which points are designated by coordinates (one for each dimension) and the distance between two points is given by a distance formula. L2 Norm is also called Euclidean norm.
In geometry, a two- or three-dimensional space in which the axioms and postulates of Euclidean geometry apply is a Euclidean space. A space in any finite number of dimensions, in which points are designated by coordinates (one for each dimension) and the distance between two points is given by a distance formula
In geometry, a two- or three-dimensional space in which the axioms and postulates of Euclidean geometry apply is a Euclidean space. A space in any finite number of dimensions, in which points are designated by coordinates (one for each dimension) and the distance between two points is given by a distance formula
Vectors
How do you add two vectors ?
(c) One Fourth Labs

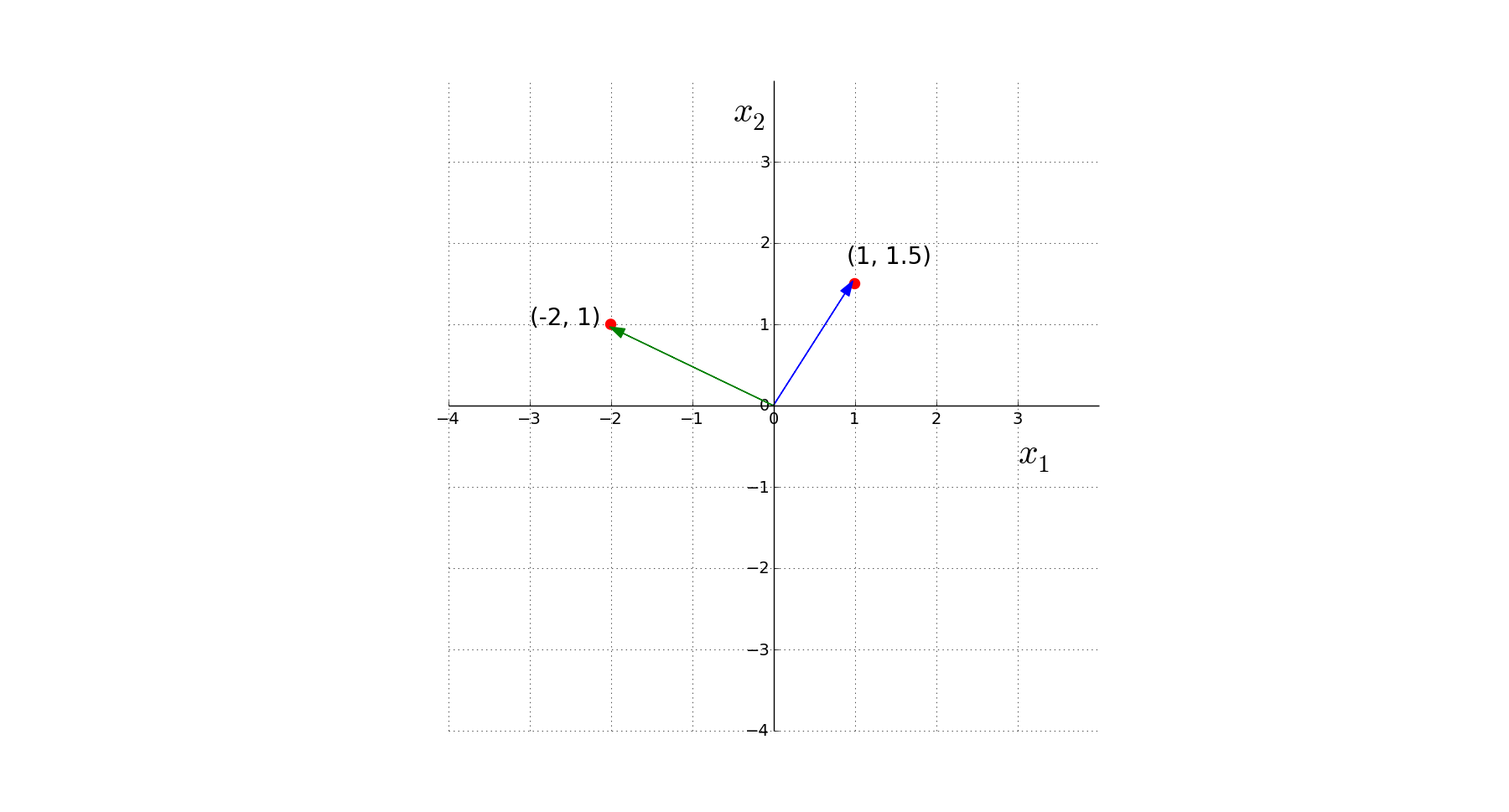
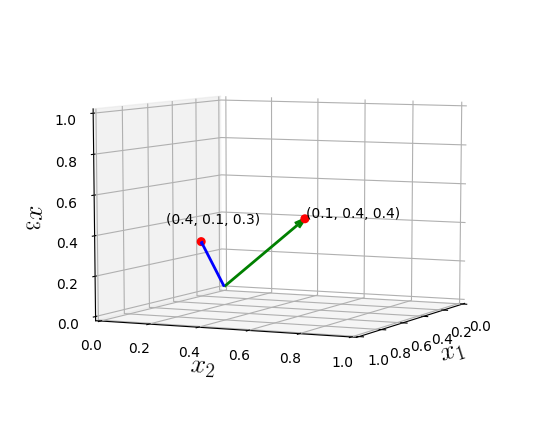
Addition
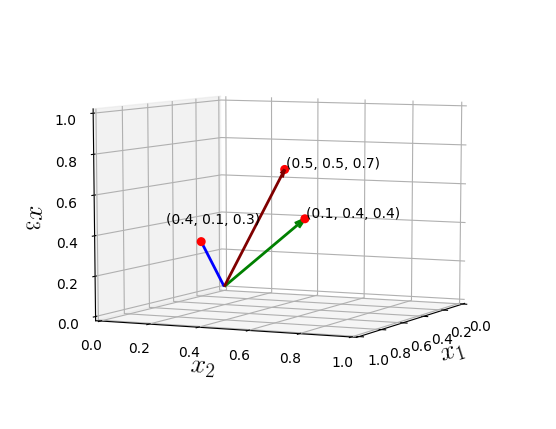


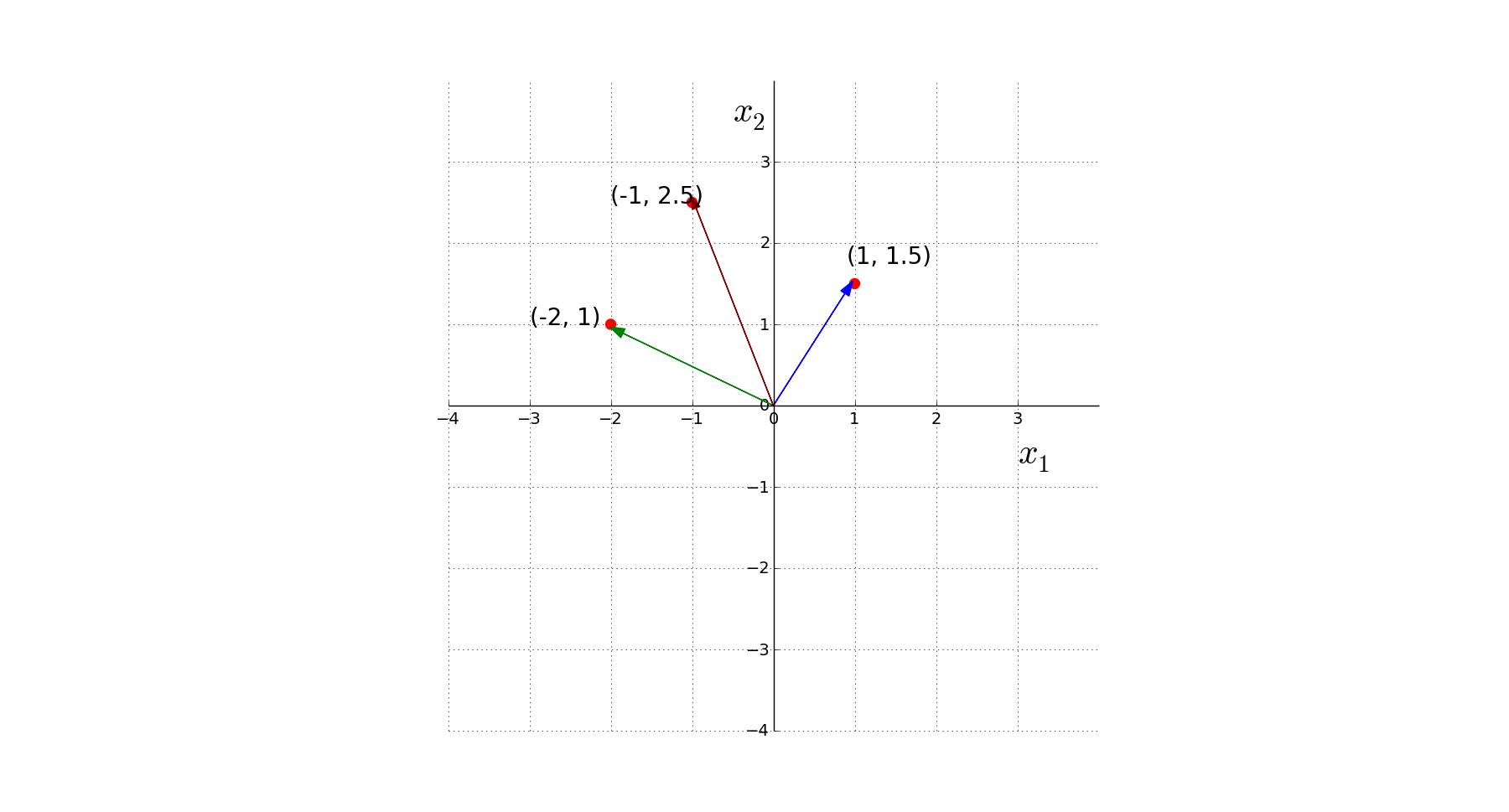
Vectors
How do you subtract two vectors ?
(c) One Fourth Labs


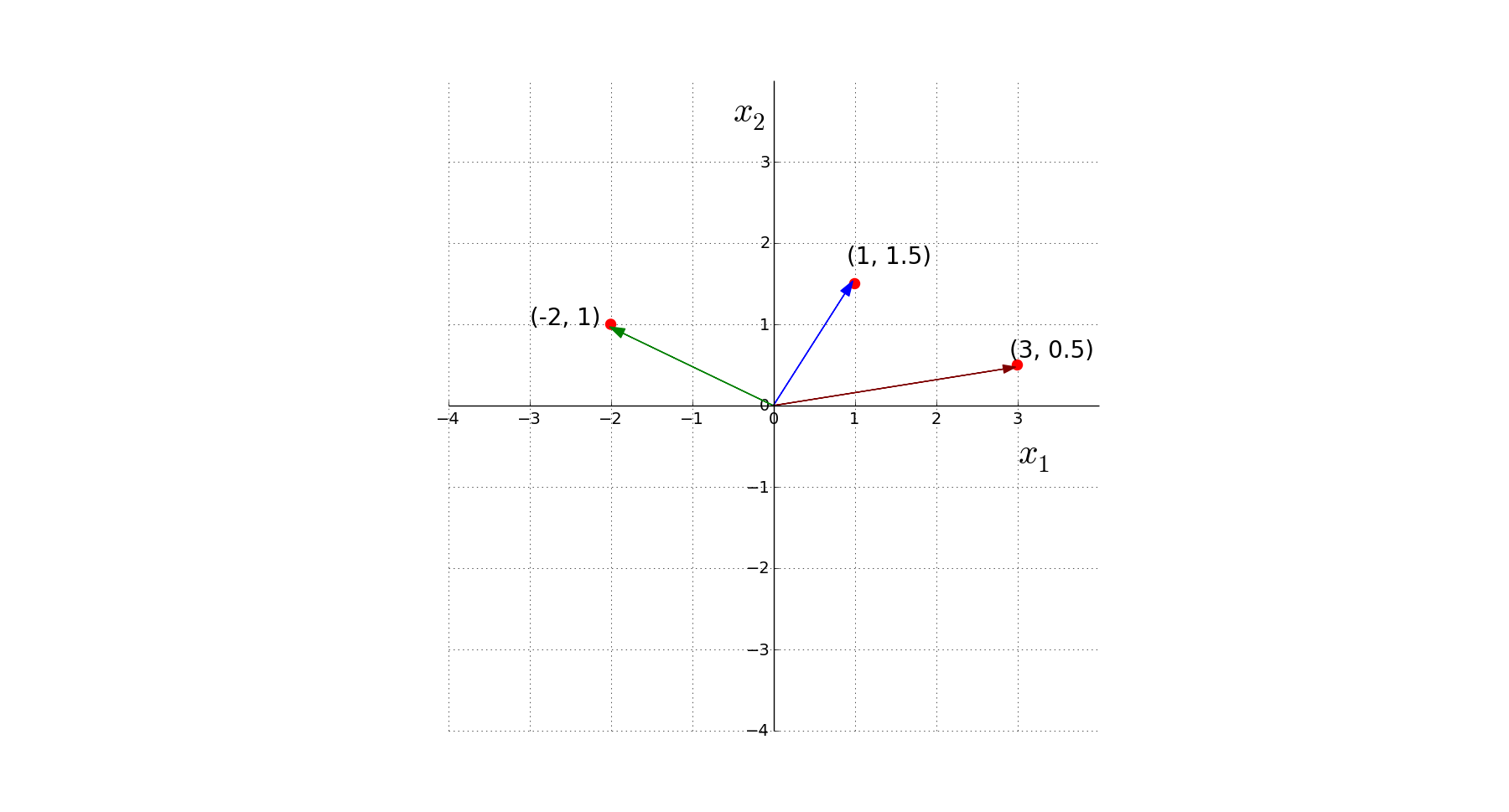
Subtraction
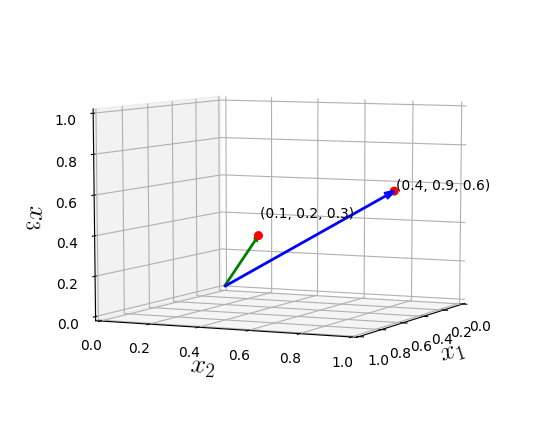

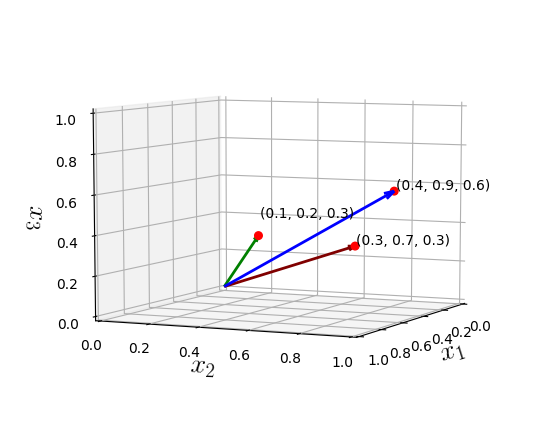

Vectors
How do you multiply two vectors ?
(c) One Fourth Labs


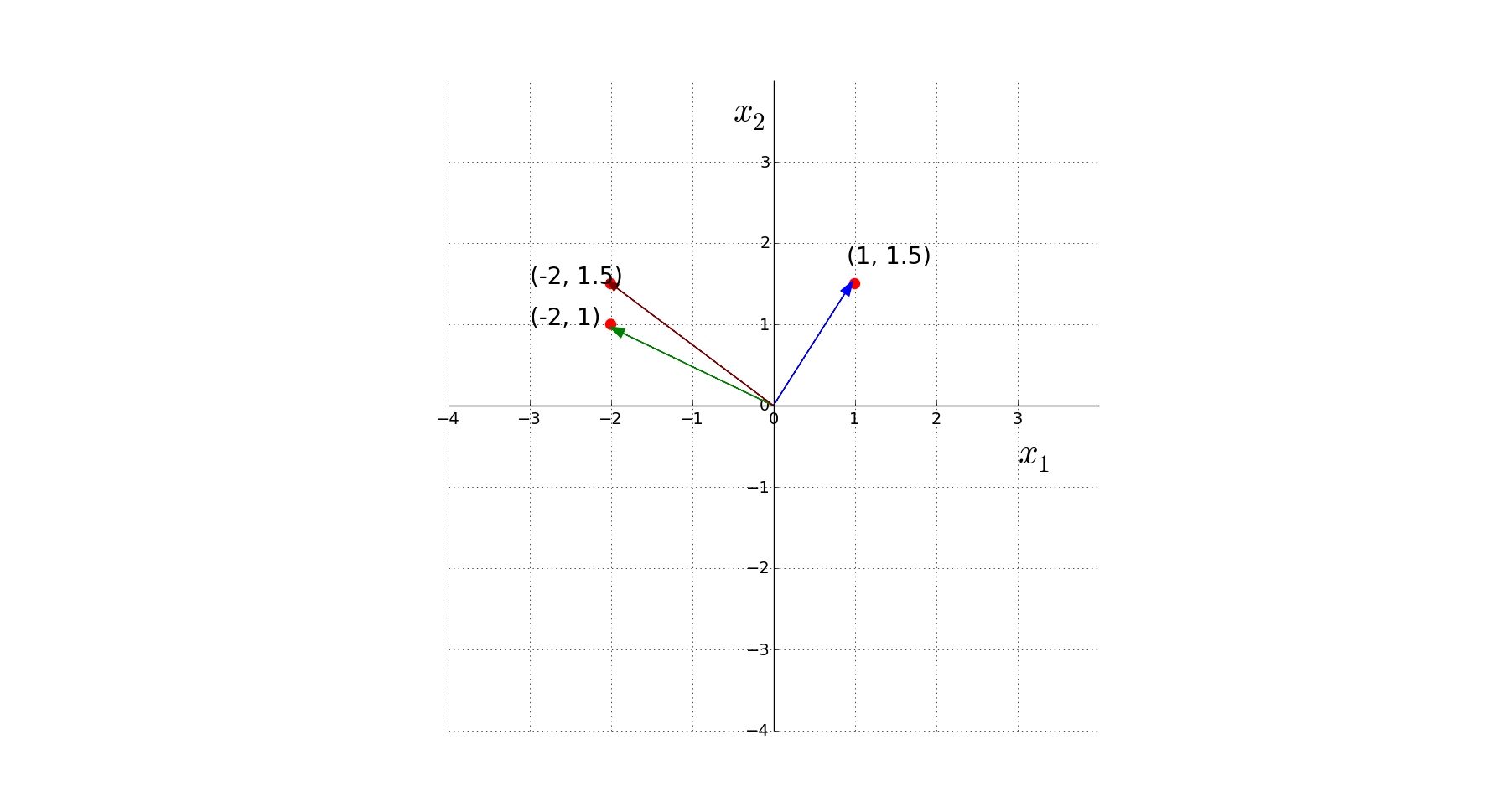
Multiply
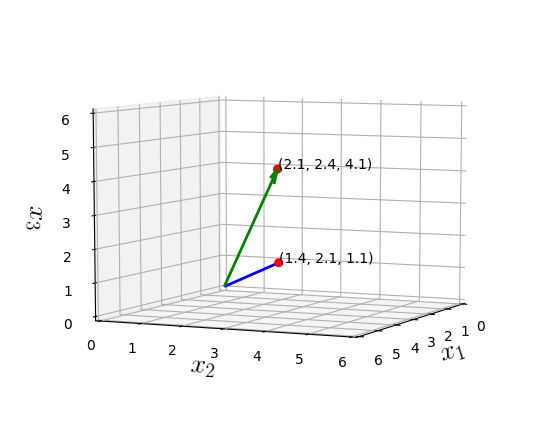

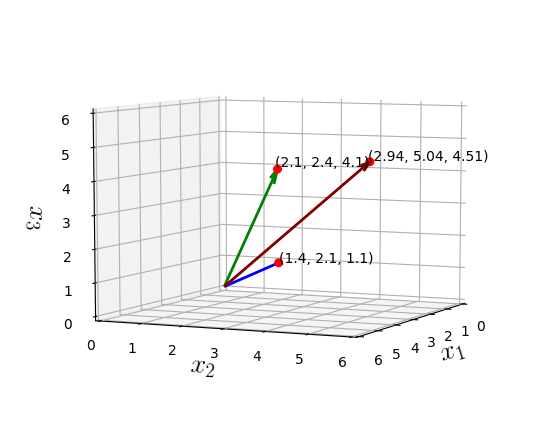

Vectors
How do you project a vector onto another ?
(c) One Fourth Labs


Vectors
How do you project a vector onto another ?
(c) One Fourth Labs


Vectors
How do you project a vector onto another ?
(c) One Fourth Labs

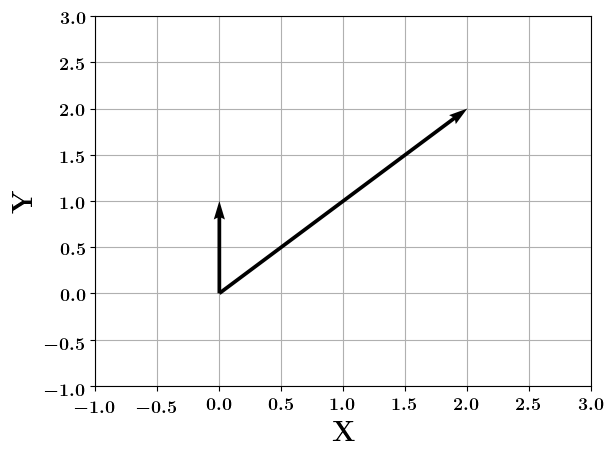
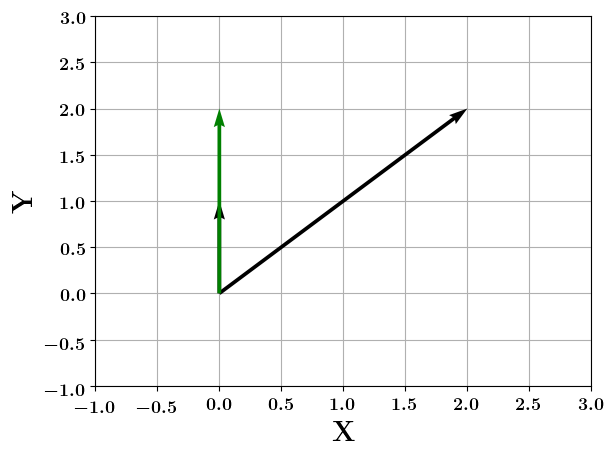
Vectors
How do you project a vector onto another ?
(c) One Fourth Labs

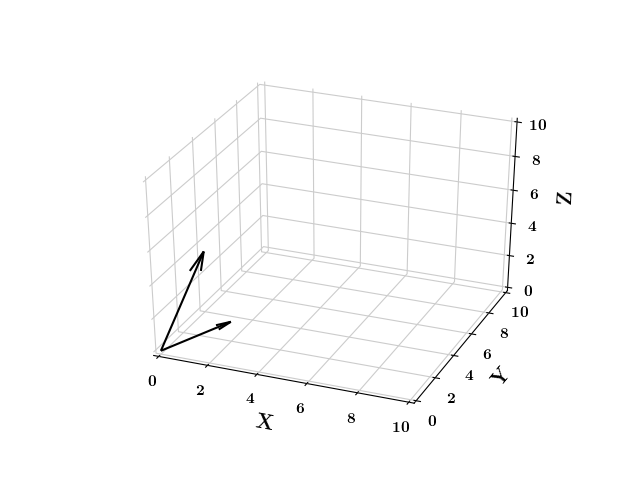
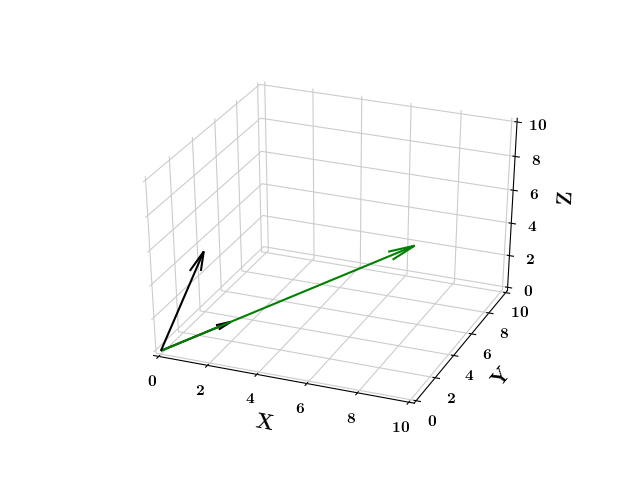
Vectors
What is a unit vector ?
(c) One Fourth Labs

"Any vector of magnitude 1 ?"
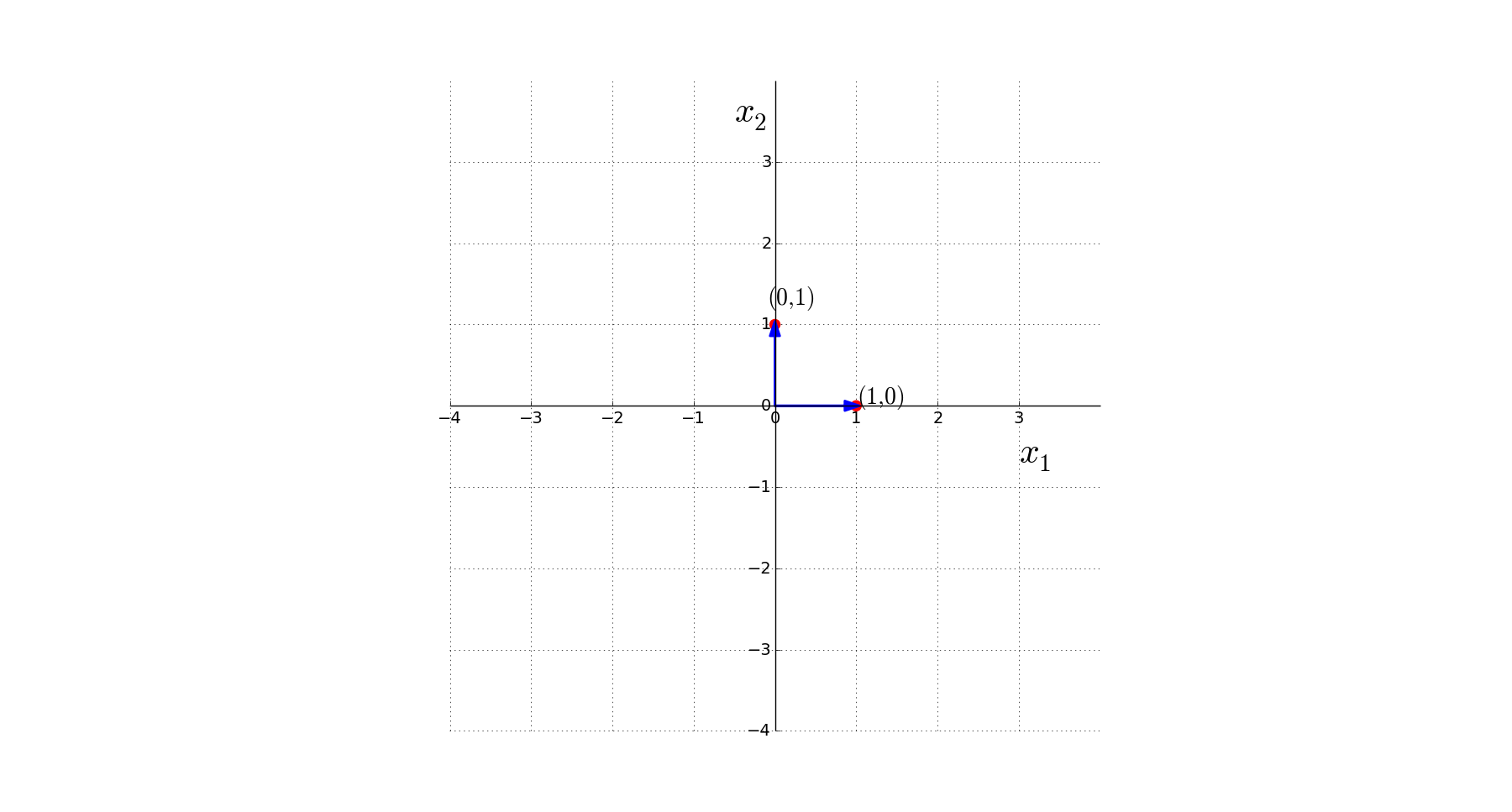
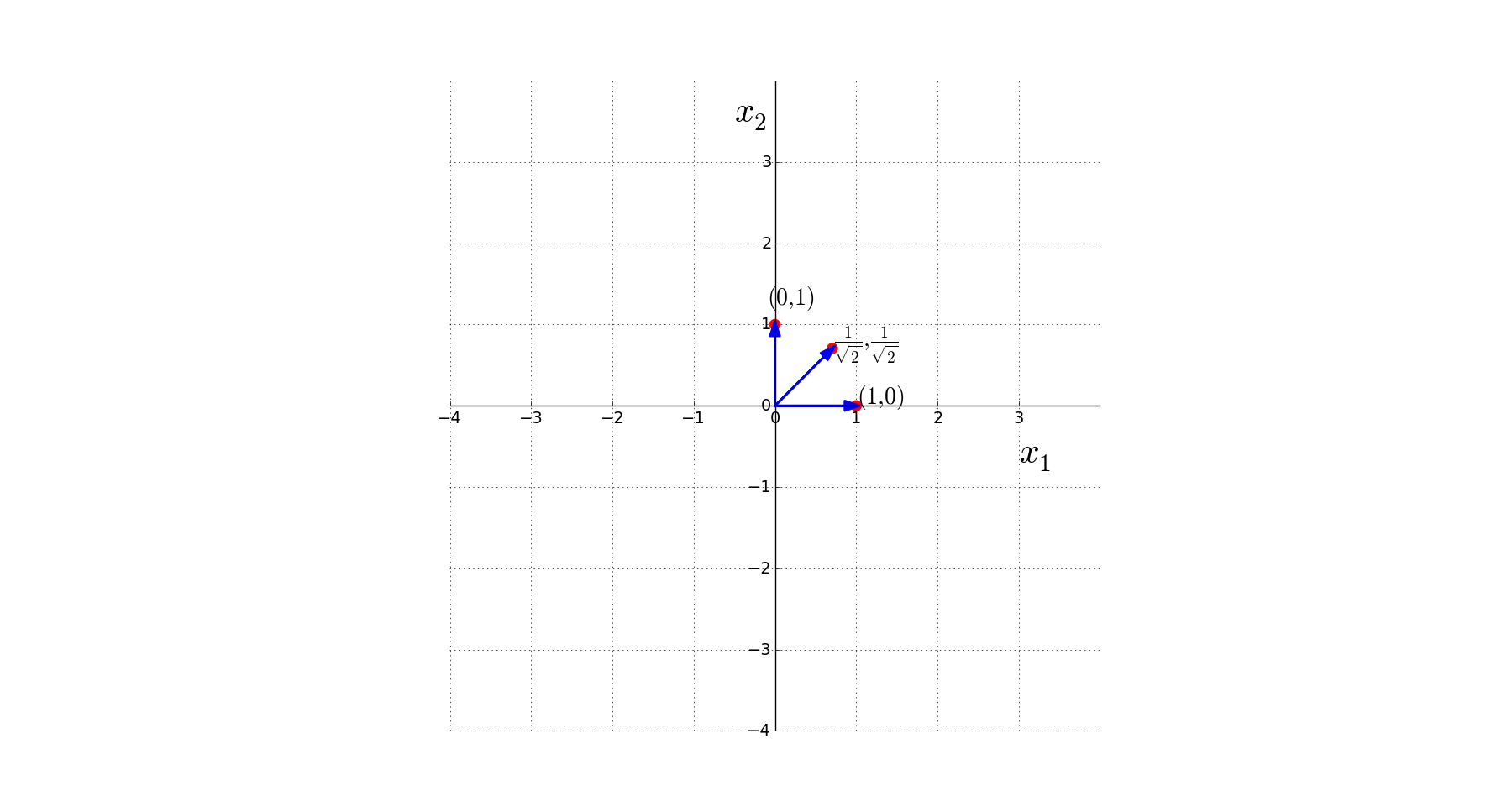
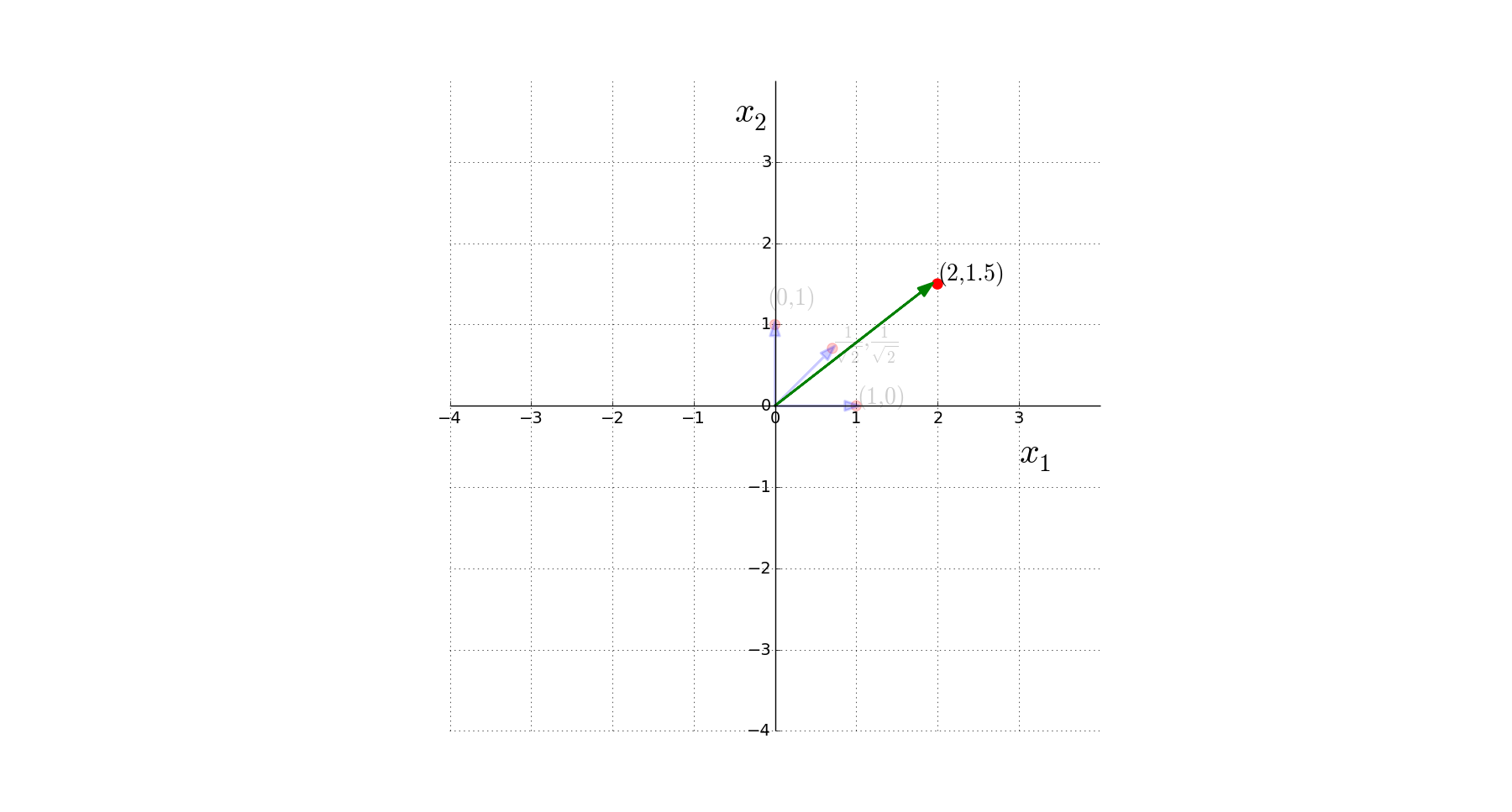
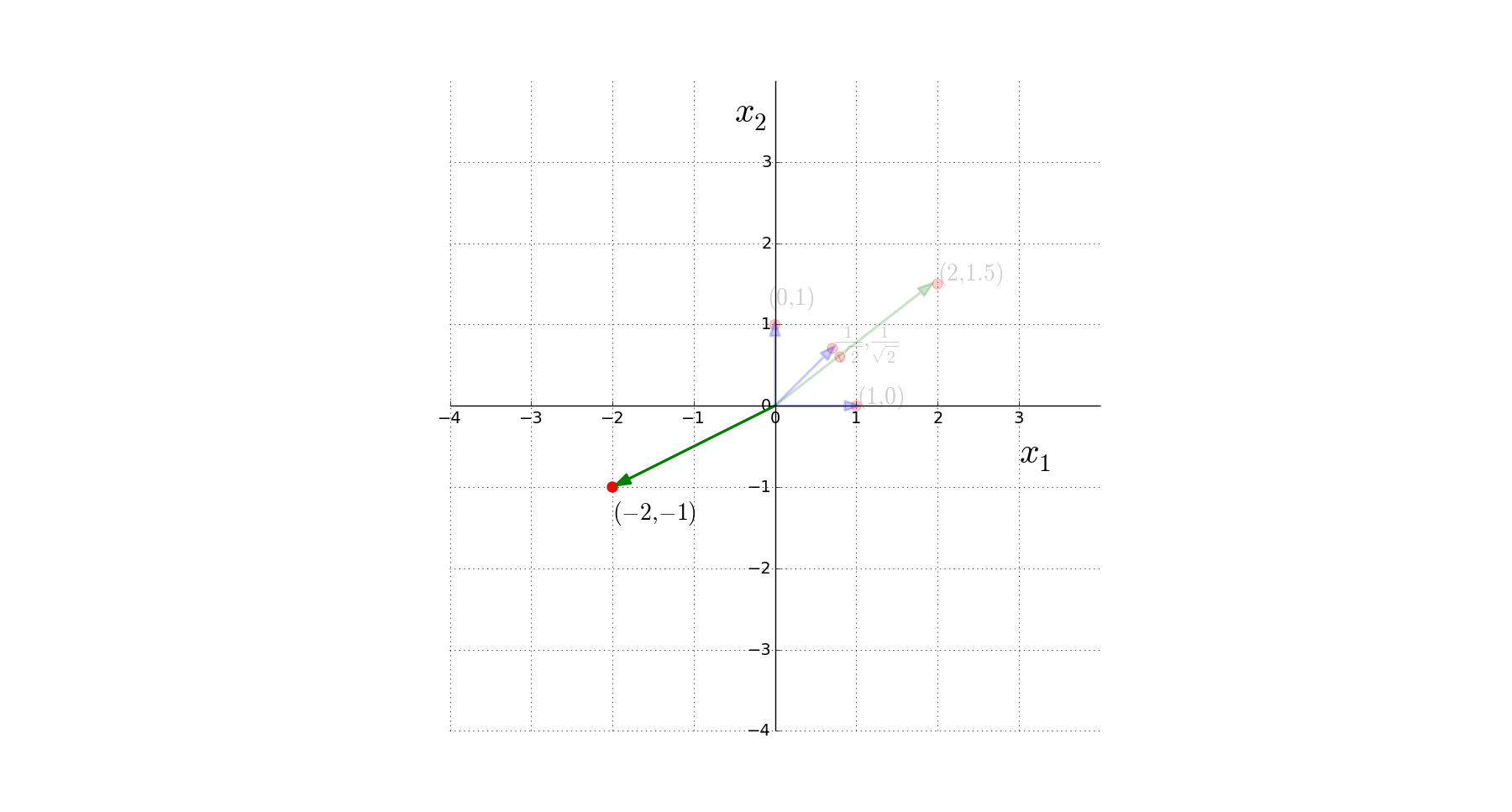
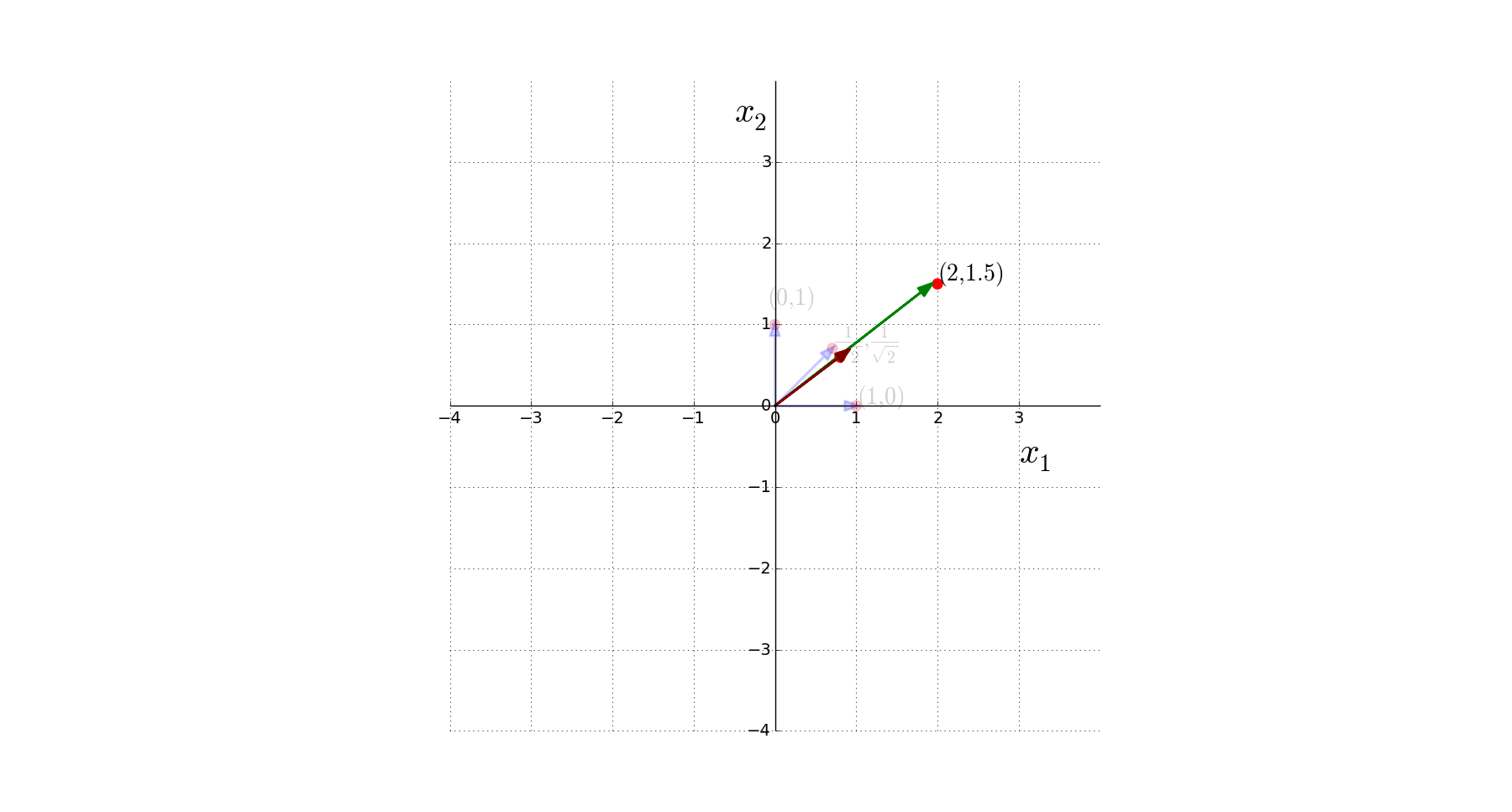




Vectors
What is a unit vector ?
(c) One Fourth Labs

Any vector of magnitude 1 ?"
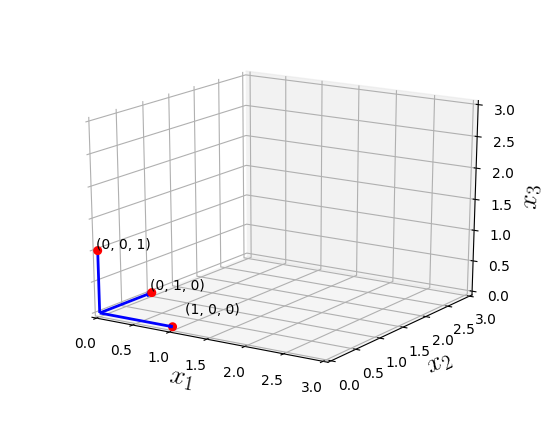
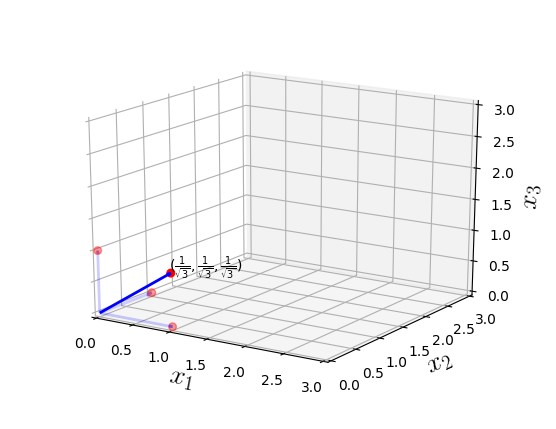
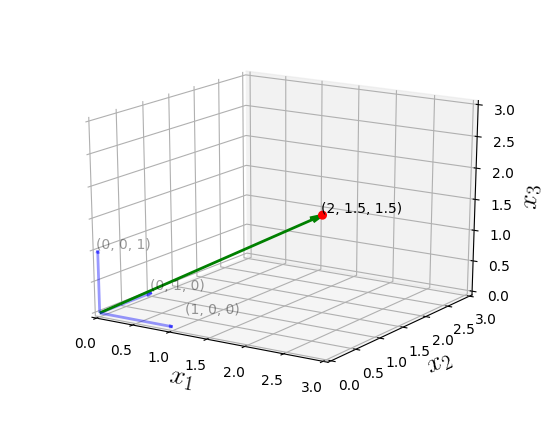
Vectors
How do you compute the angle between two vectors ?
(c) One Fourth Labs

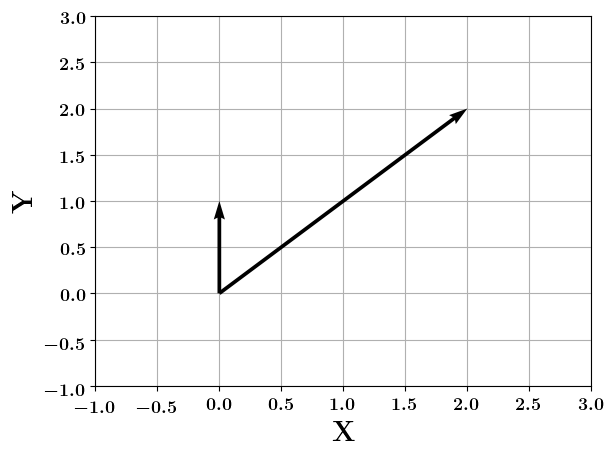
Vectors
How do you compute the angle between two vectors ?
(c) One Fourth Labs

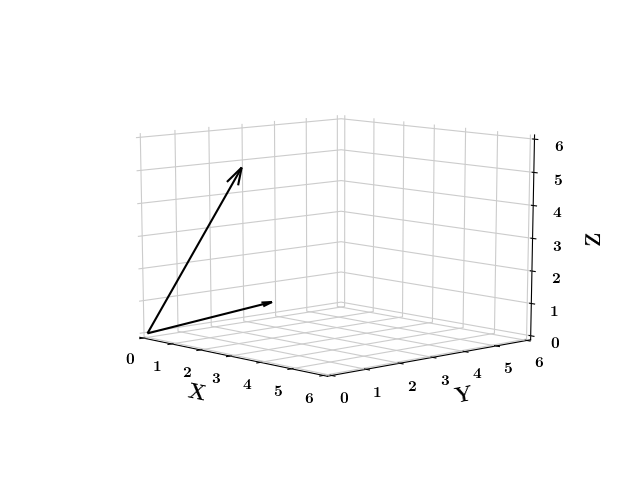
Vectors
What are orthogonal vectors?
(c) One Fourth Labs

- Orthogonal
Perpendicular
Vectors
What are orthogonal vectors?
(c) One Fourth Labs

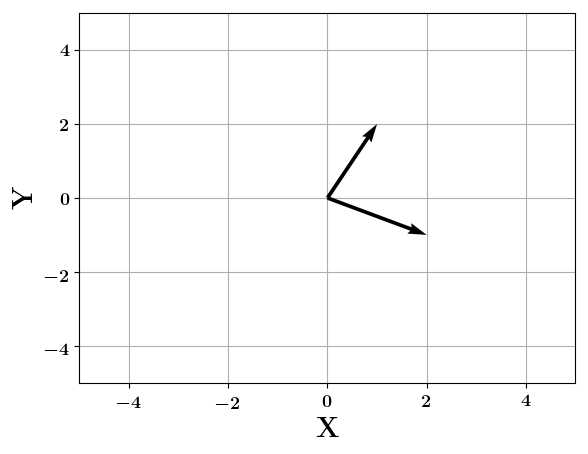
Vectors
What are orthogonal vectors?
(c) One Fourth Labs

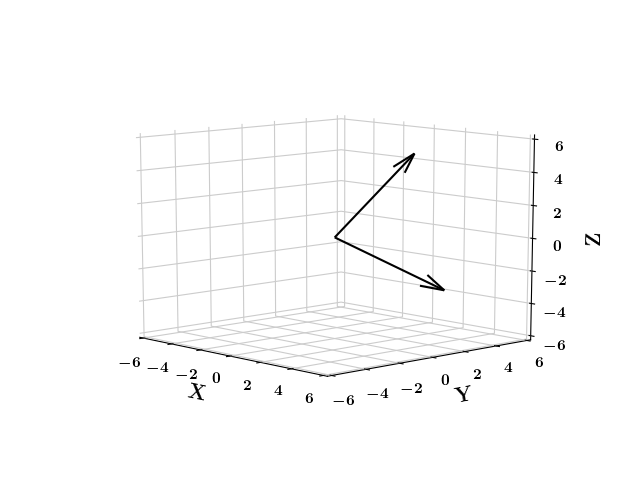
Vectors
What are orthogonal vectors?
(c) One Fourth Labs

Vectors
Why do we care about them ?
(c) One Fourth Labs



Matrices
What are they ?
(c) One Fourth Labs

column vector
row vector
Matrices
How do you add two matrices ?
(c) One Fourth Labs

Matrices
How do you multiply a matrix with a vector ?
(c) One Fourth Labs

Matrices
How do you multiply a matrix with a vector ?
(c) One Fourth Labs

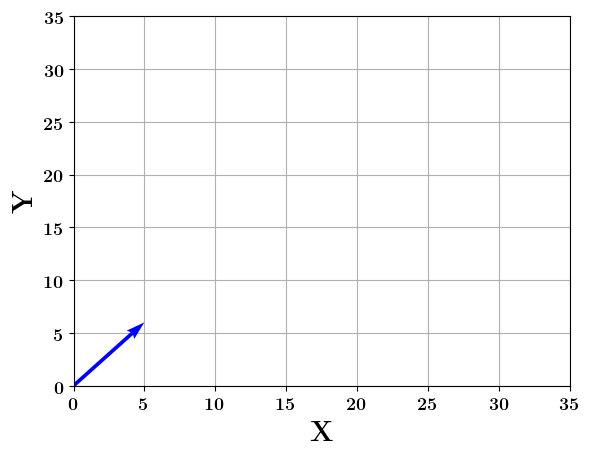
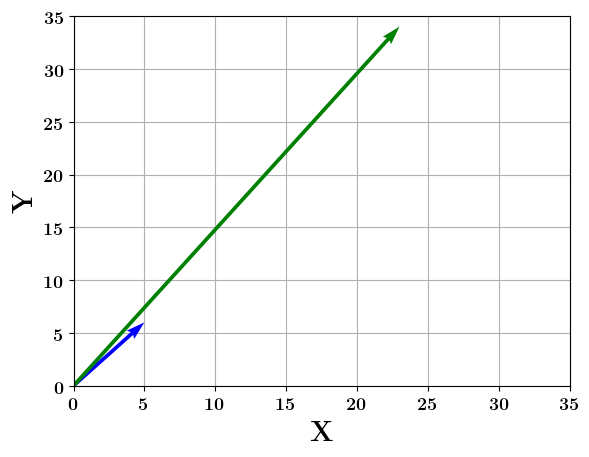
- What happens when a matrix hits a vector?
- The vector gets transformed into a new vector (it strays from its path).
- The vector may also get scaled (elongated or shortened) in the process.
Matrices
How do you multiply a matrix with a vector ?
(c) One Fourth Labs

Matrices
How do you multiply a matrix with a vector ?
(c) One Fourth Labs

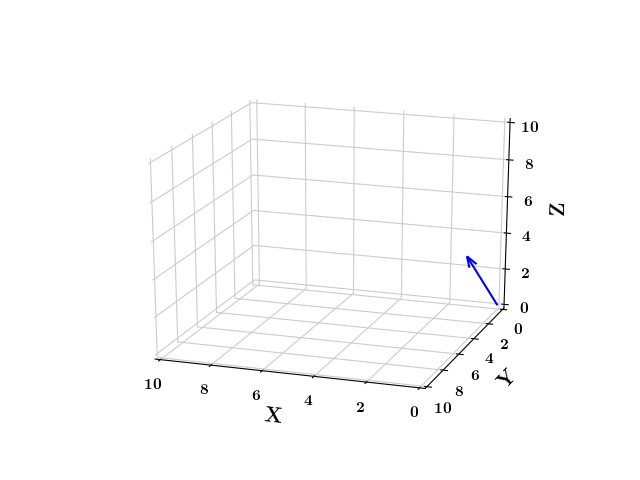
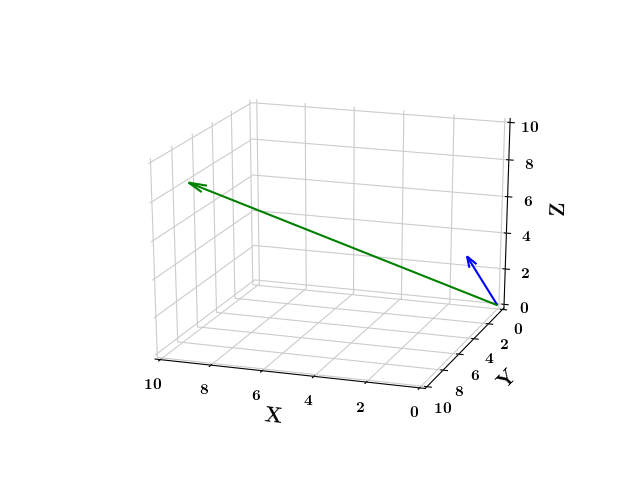
Similarly, in a 3D space, when a vector is hit by a matrix, it gets transformed into a new vector.
Matrices
How do you multiply a matrix with a vector ?
(c) One Fourth Labs

illegal operation
Matrices
How do you multiply a matrix with a vector ?
(c) One Fourth Labs

legal operation
Conclusion : Number of columns in the matrix should be the same as the number of rows in the vector.
Matrices
How do you multiply two matrices ?
(c) One Fourth Labs

Matrices
How do you multiply two matrices ?
(c) One Fourth Labs

Number of columns in the matrix is not equal to the number of rows in the vector.
Matrices
How do you multiply two matrices ?
(c) One Fourth Labs

Number of columns in the matrix is equal to the number of rows in the vector.
Matrices
How do you multiply two matrices ?
(c) One Fourth Labs

Conclusion : Any m x n matrix can be multiplied with a n x k matrix to get a m x k output.
Matrices
Is there an alternate way of multiplying matrices ?
(c) One Fourth Labs

Matrices
Is there an alternate way of multiplying matrices ?
(c) One Fourth Labs

Matrices
What is the common operation that you will see in this course ?
(c) One Fourth Labs


| Weight (g) | Screen Size(in.) | Dual SIM | Radio | Battery (mAh) | Price (INR) | Internal Memory (GB) |
|---|

| 151 | 5.8 | 1 | 1 | 3060 | 15000 | 64 |
| 180 | 6.18 | 1 | 0 | 3500 | 32000 | 64 |
| 160 | 5.84 | 0 | 0 | 3060 | 25000 | 64 |
| 205 | 6.2 | 0 | 1 | 5000 | 18000 | 64 |
| 162 | 5.9 | 0 | 1 | 3000 | 14000 | 64 |
| 182 | 6.26 | 1 | 1 | 4000 | 12000 | 64 |
| 138 | 4.7 | 0 | 0 | 1960 | 35000 | 64 |
| 185 | 6.41 | 1 | 0 | 3700 | 42000 | 64 |
| 170 | 5.5 | 0 | 0 | 3260 | 44000 | 64 |
Why do we care about them ?
(c) One Fourth Labs
Matrices








Why do we care about them ?
(c) One Fourth Labs
Matrices








| F1 | F2 | F3 | F4 | F5 | F6 | Fn |
|---|

Why do we care about them ?
(c) One Fourth Labs
Matrices
| F1 | F2 | F3 | F4 | F5 | F6 | ... | Fn |
|---|








final
By preksha nema
final
matrices
- 998



