1.8 Representation Power of functions
Why do we need complex functions ?

Recap: Six jars
What we saw in the previous chapter?
(c) One Fourth Labs


None of them handle non-linear separable data
Why do we care about continuous functions ?
(c) One Fourth Labs

1. On LHS show the update equations for w and b and write down that \deltaw=partial derivative \deltab=partial derivative
2. On RHS show examples of smooth functions, sigmoid in 2d, asymmetric sigmoid in 3d (w1 !=w2!=0), some other complex function in 3d. For each of the 3 examples contrast it with a non-continuous function. Show the equations also below the plots
Recap: Continuous Functions
Modeling Complex Relations
Why do we need complex functions ?
(c) One Fourth Labs

\( x_1 \)
\(x_2\)
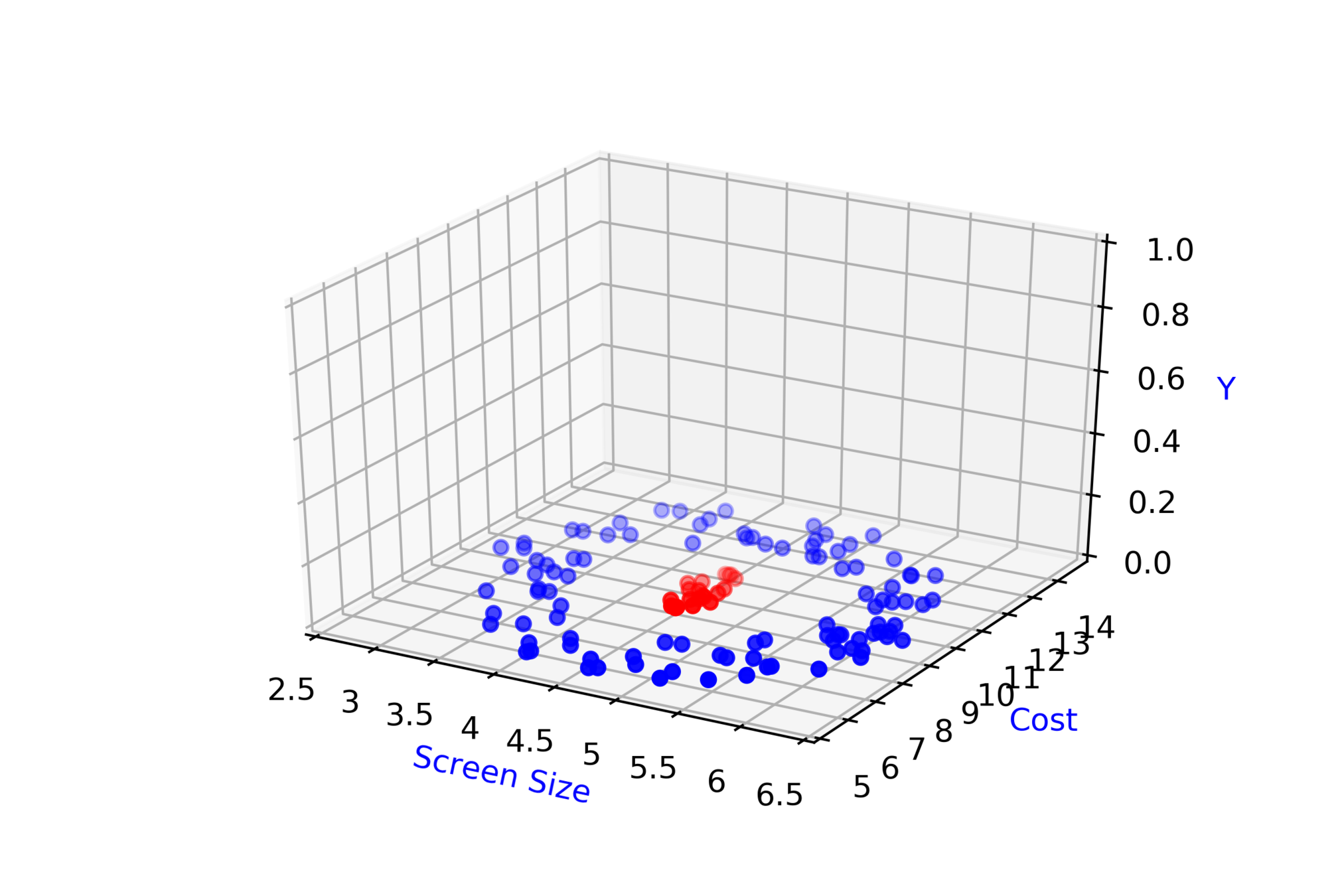
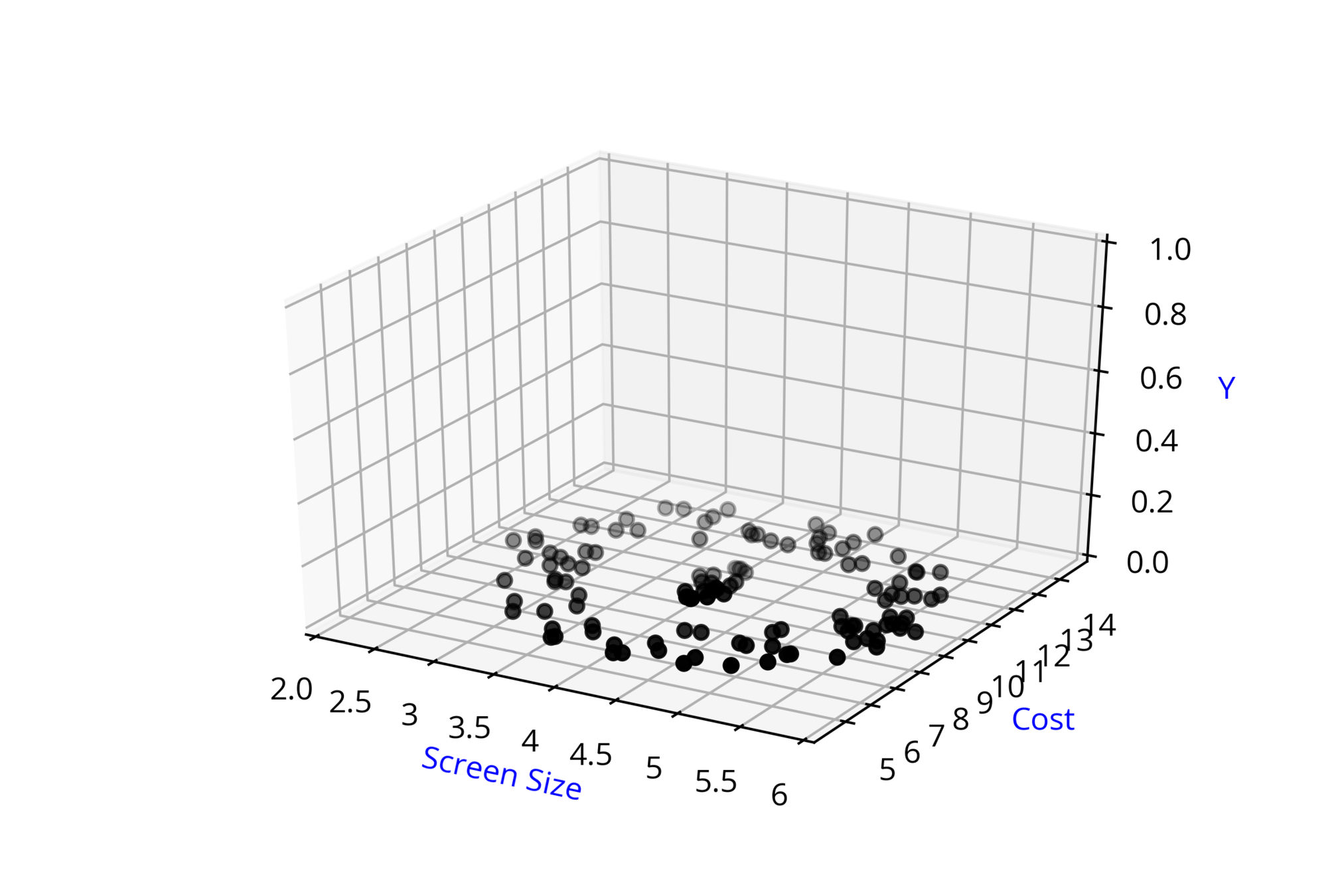
Screen Size
Cost
3.5
4.5
8k
12k

\( \hat{y} = 1\)
\( \hat{y} = 0 \)



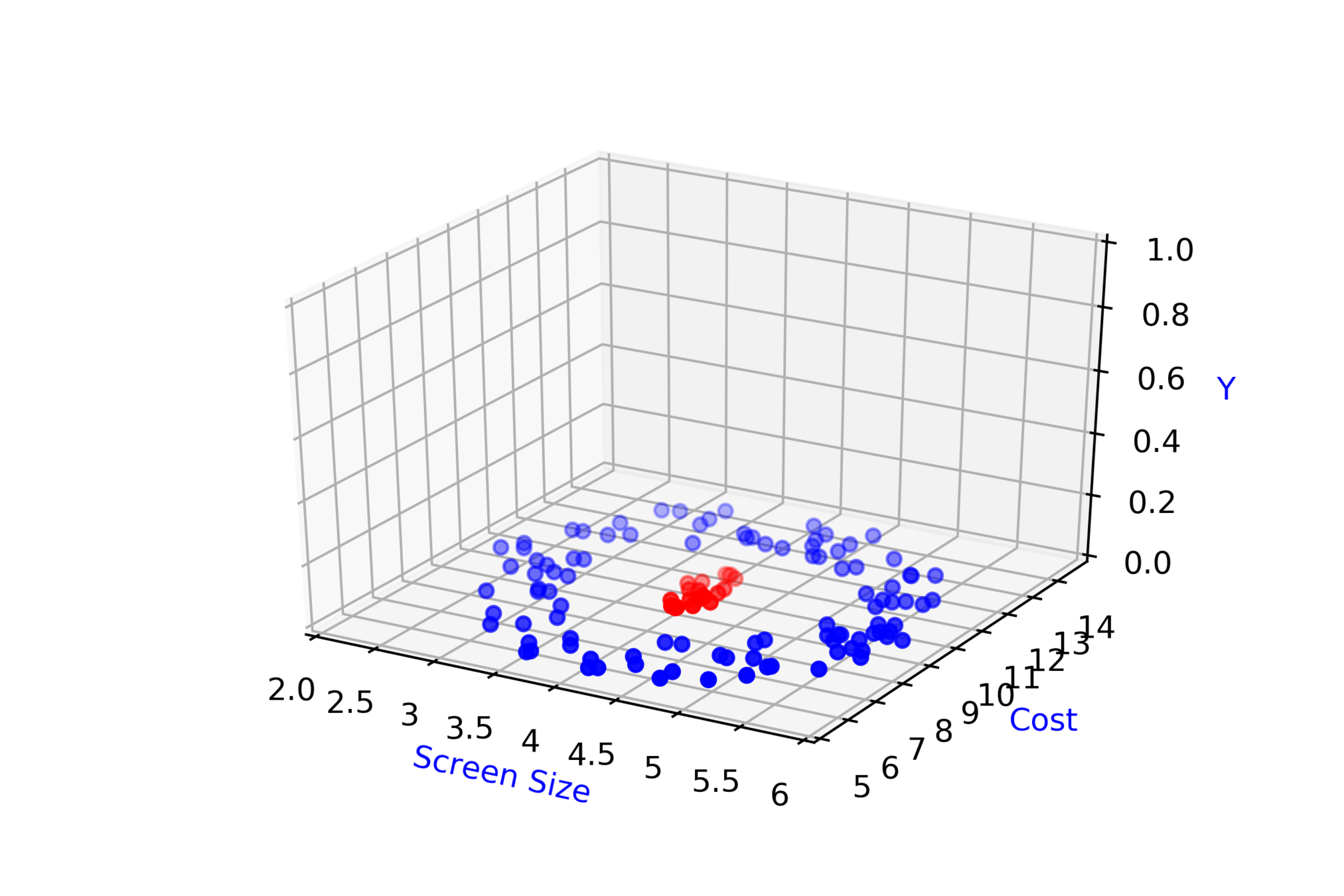
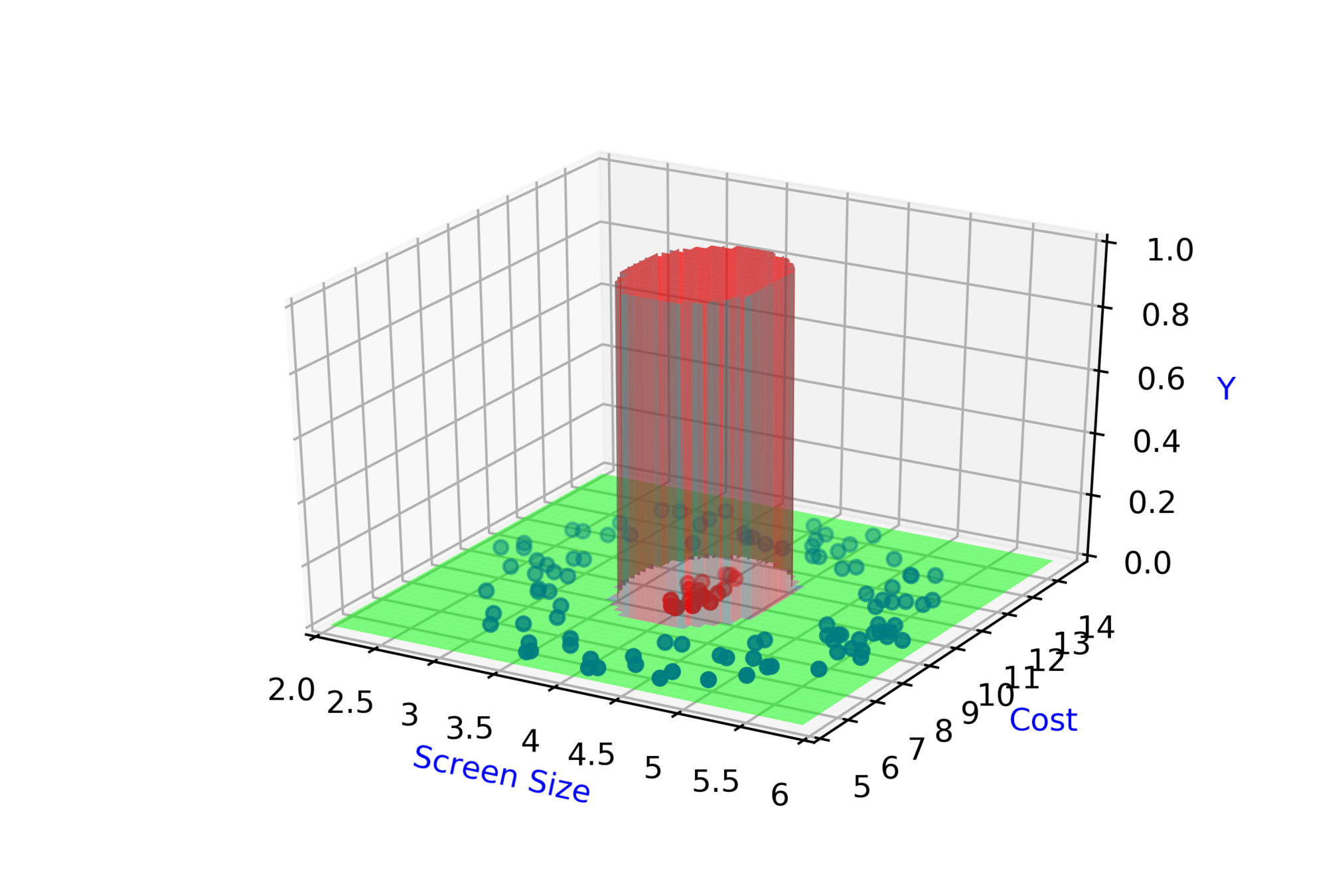
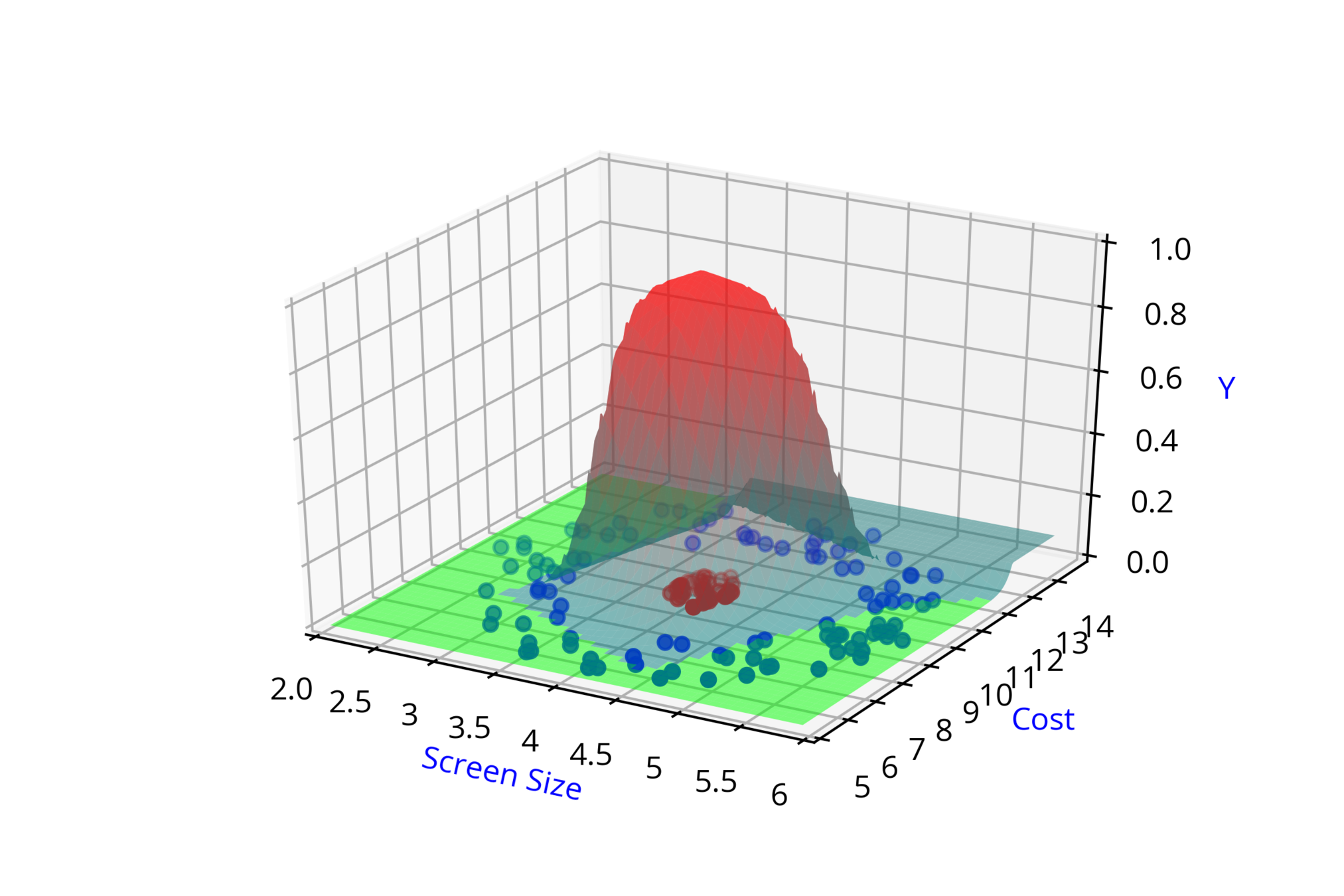
\( \hat{y} = \hat{f}(x_1,x_2) \)
\( \hat{y} =\hat{f}(\hat{y_1},\hat{y_2},\hat{y_3},\hat{y_4}, w_9, w_{10}, w_{11},w_{12}, b_{5} )\)
\( \hat{y_2} = \hat{f}(x_1,x_2,w_3,w_4,b_2) \)
\( \hat{y_1} = \hat{f}(x_1,x_2,w_1,w_2,b_1) \)
\( \hat{y_3} = \hat{f}(x_1,x_2,w_5,w_6,b_3) \)
\( \hat{y_4} = \hat{f}(x_1,x_2,w_7,w_8,b_4) \)
Modeling Complex Relations
Why do we need complex functions ?
(c) One Fourth Labs

\( x_1 \)
\(x_2\)
Screen Size
Cost
3.5
4.5
8k
12k
\( \hat{y} = \hat{f}(x_1,x_2) \)

\( \hat{y} = 1\)
\( \hat{y} = 0 \)
\( \hat{y} =\hat{f}(\hat{y_1},\hat{y_2},\hat{y_3},\hat{y_4}, w_9, w_{10}, w_{11},w_{12}, b_{5} )\)





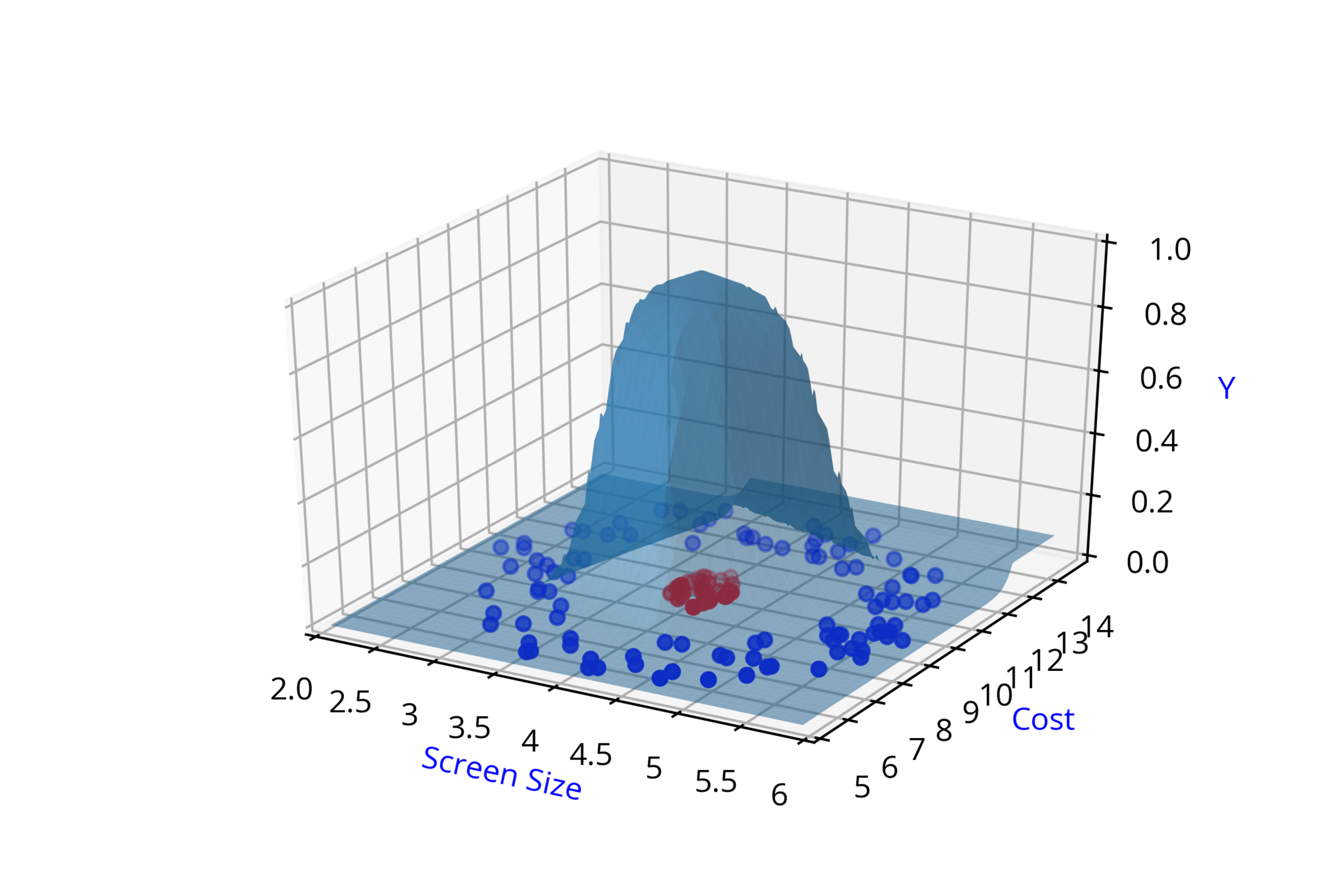
\( \hat{y_2} = \hat{f}(x_1,x_2,w_3,w_4,b_2) \)
\( \hat{y_1} = \hat{f}(x_1,x_2,w_1,w_2,b_1) \)
\( \hat{y_3} = \hat{f}(x_1,x_2,w_5,w_6,b_3) \)
\( \hat{y_4} = \hat{f}(x_1,x_2,w_7,w_8,b_4) \)
Modeling Complex Relations
Why do we need complex functions ?
(c) One Fourth Labs

\( \hat{y} = \hat{f}(x_1,x_2) \)
\( \hat{y} =\hat{f}(\hat{y_1},\hat{y_2},\hat{y_3},\hat{y_4}, w_9, w_{10}, w_{11},w_{12}, b_{5} )\)
\( \hat{y_2} = \hat{f}(x_1,x_2,w_3,w_4,b_2) \)
\( \hat{y_1} = \hat{f}(x_1,x_2,w_1,w_2,b_1) \)
\( \hat{y_3} = \hat{f}(x_1,x_2,w_5,w_6,b_3) \)
\( \hat{y_4} = \hat{f}(x_1,x_2,w_7,w_8,b_4) \)
\( \hat{y} = \frac{1}{1+e^{-(w_1* x_1 + w_2*x_2+b)}} \)

\(w_1\)
\(w_2\)
\(x_2\)
\(x_1\)
\( \hat{y} \)
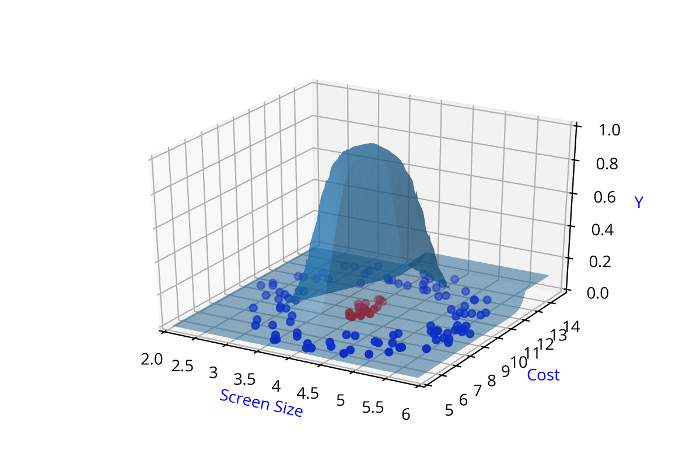


Are such complex functions seen in most real world examples ?
If so, how do I even come up with such complex functions?
Modeling Complex Relations
Are such complex functions seen in most real world examples ?
(c) One Fourth Labs

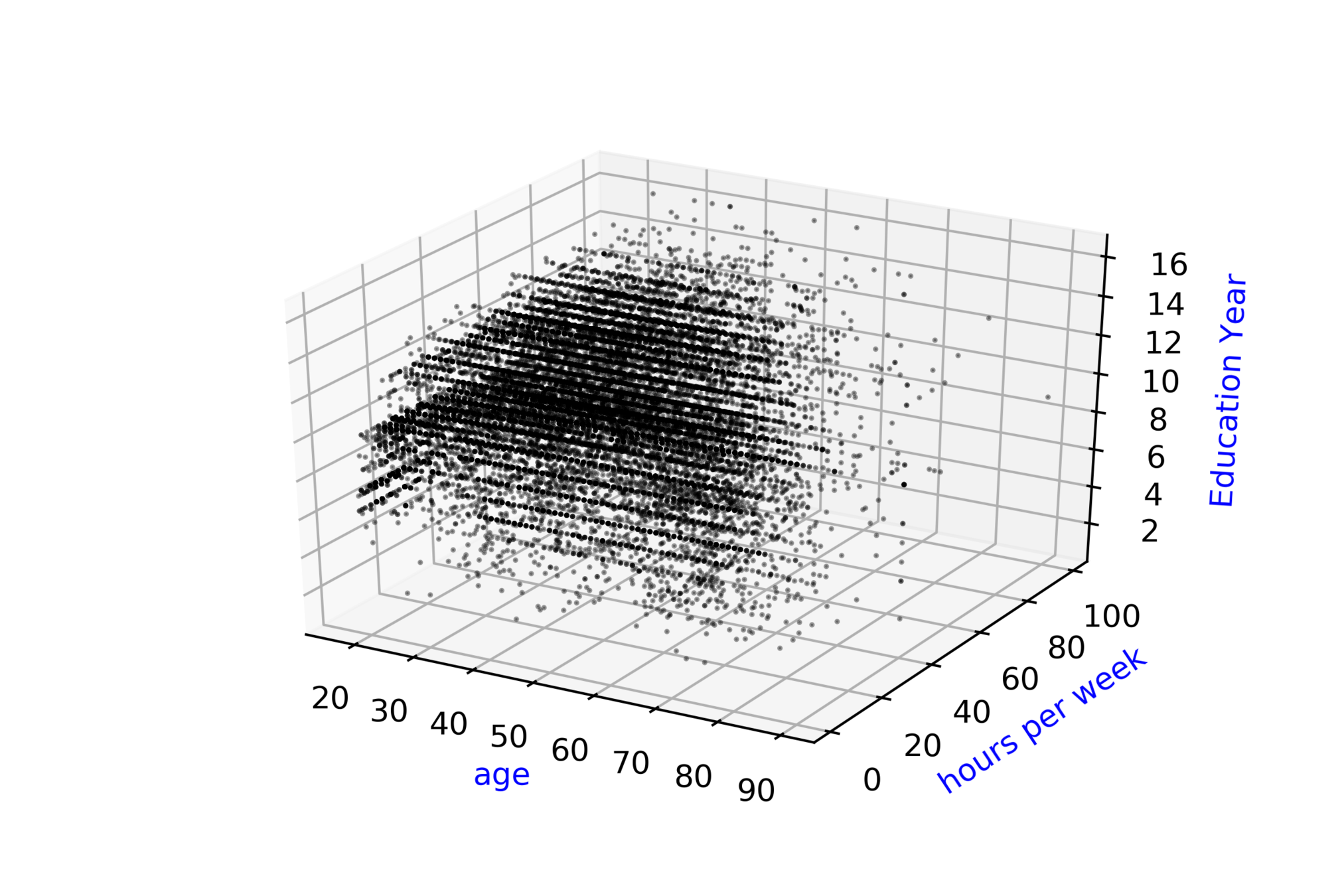
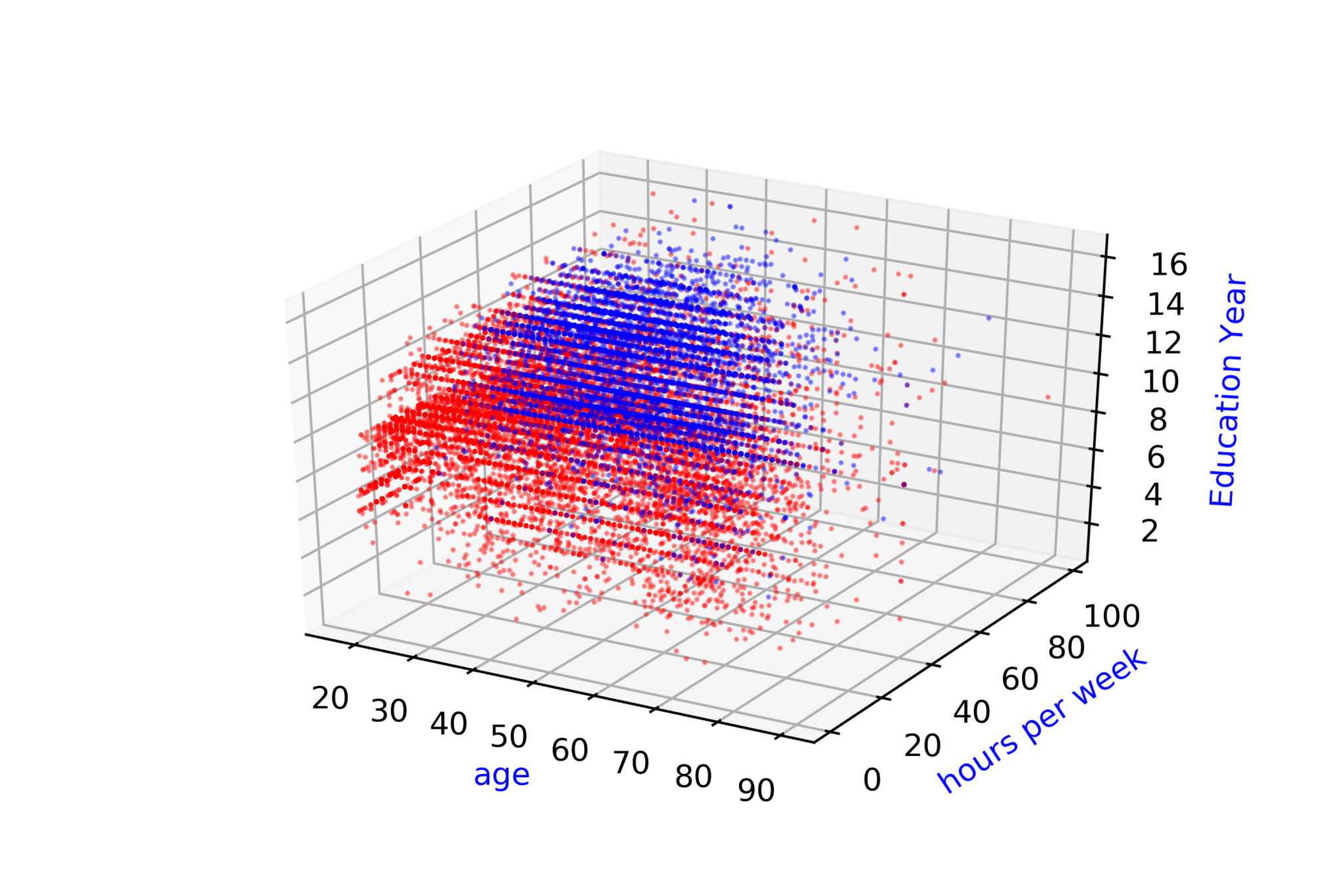
Adult Census Income\( ^{*} \)
Whether Annual Income of person \( \geq \) 50k or \( < \) 50k ?
| Age |
| 90 |
| 54 |
| 74 |
| 45 |
| hour/week |
| 40 |
| 40 |
| 20 |
| 35 |
| Education year |
| 9 |
| 4 |
| 16 |
| 16 |
| Income |
| 0 |
| 0 |
| 1 |
| 1 |
\( \hat{y} = \hat{f}(x_1, x_2, .... ,x_{14}) \)
\( \hat{income} = \hat{f}(age,hour, ...,education) \)
Modeling Complex Relations
Are such complex functions seen in most real world examples ?
(c) One Fourth Labs

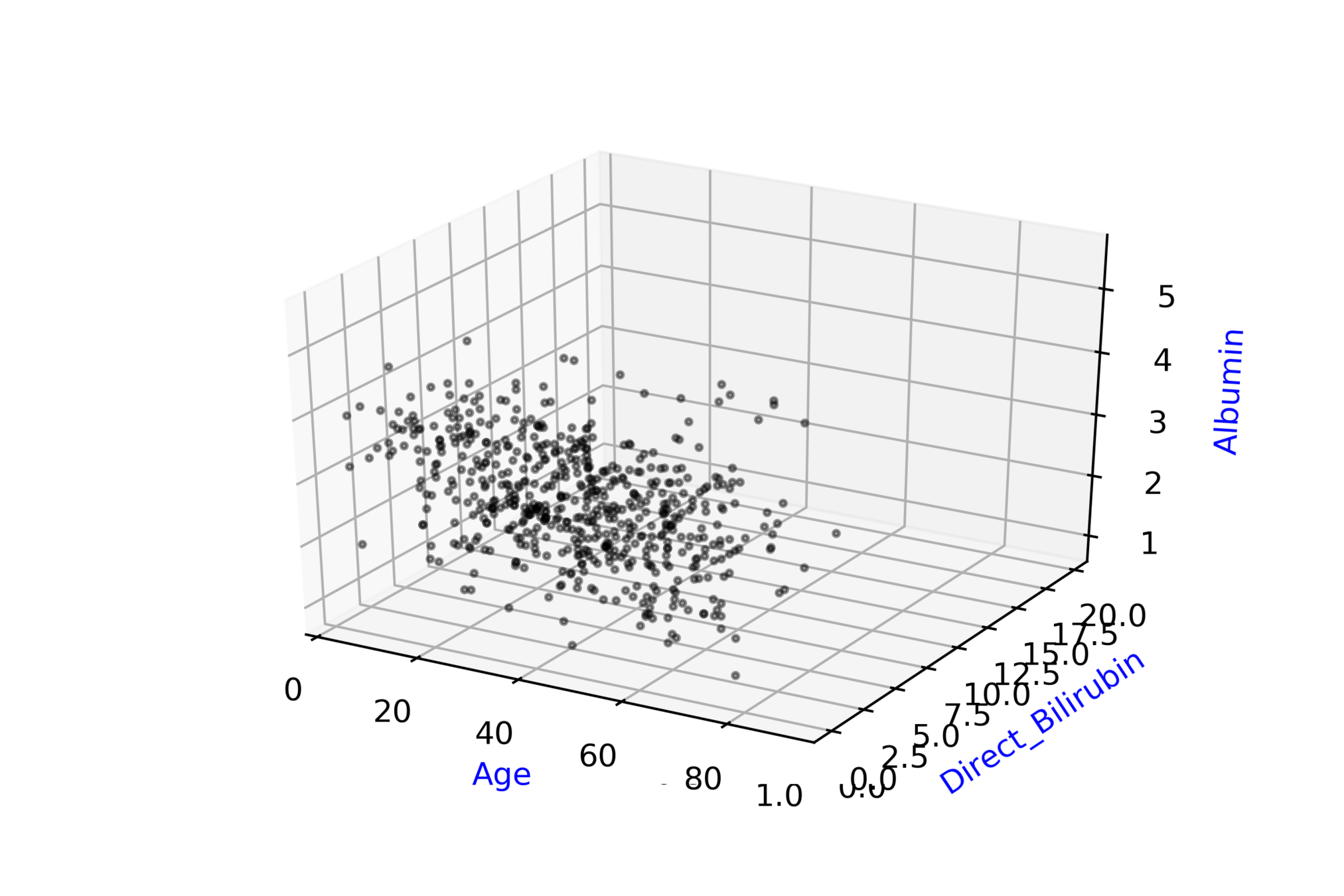
Indian Liver Patient Records\( ^{*} \)
whether person needs to be diagnosed or not ?
| Age |
| 65 |
| 62 |
| 20 |
| 84 |
| Albumin |
| 3.3 |
| 3.2 |
| 4 |
| 3.2 |
| T_Bilirubin |
| 0.7 |
| 10.9 |
| 1.1 |
| 0.7 |
| D |
| 0 |
| 0 |
| 1 |
| 1 |
\( \hat{y} = \hat{f}(x_1, x_2, .... ,x_{10}) \)
\( \hat{D} = \hat{f}(Age, Albumin, .... ,T\_Bilirubin) \)
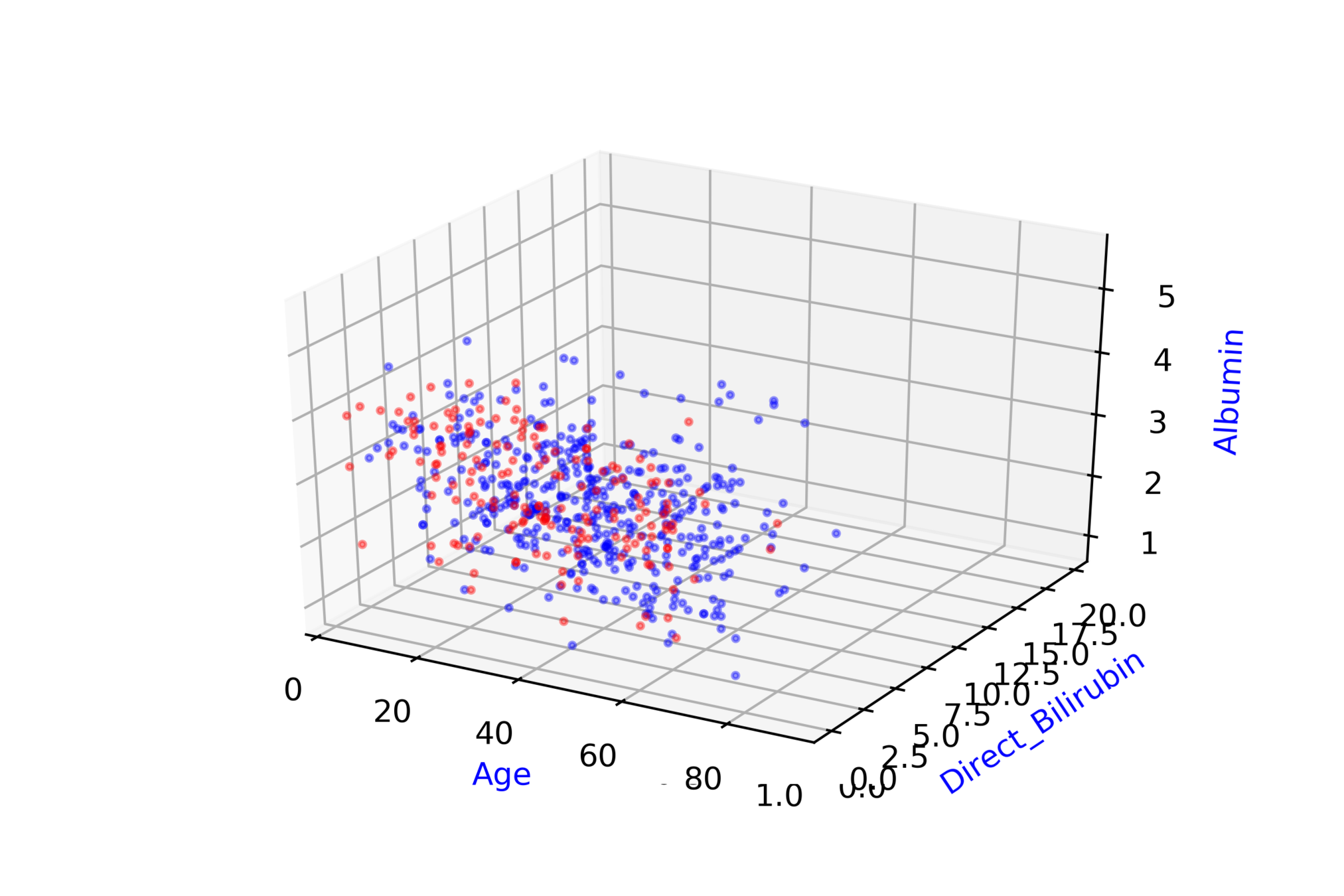
Modeling Complex Relations
Are such complex functions seen in most real world examples ?
(c) One Fourth Labs

*https://www.kaggle.com/c/titanic/data
Titanic: Machine Learning from Disaster\( ^{*} \)
Predict survival on the Titanic
| Ticket class |
| 93.85 |
| -141.22 |
| -65.2 |
| 142.4 |
| # of siblings |
| 83.81 |
| -81.79 |
| -76.33 |
| 137.03 |
| Fare |
| 20.1 |
| -52.28 |
| -76.23 |
| 93.65 |
| Survived ? |
| 0 |
| 1 |
| 0 |
| 1 |
\( \hat{y} = \hat{f}(x_1, x_2, .... ,x_{9}) \)
\( \hat{D} = \hat{f}(ticket\_class, fare, .... ,age) \)
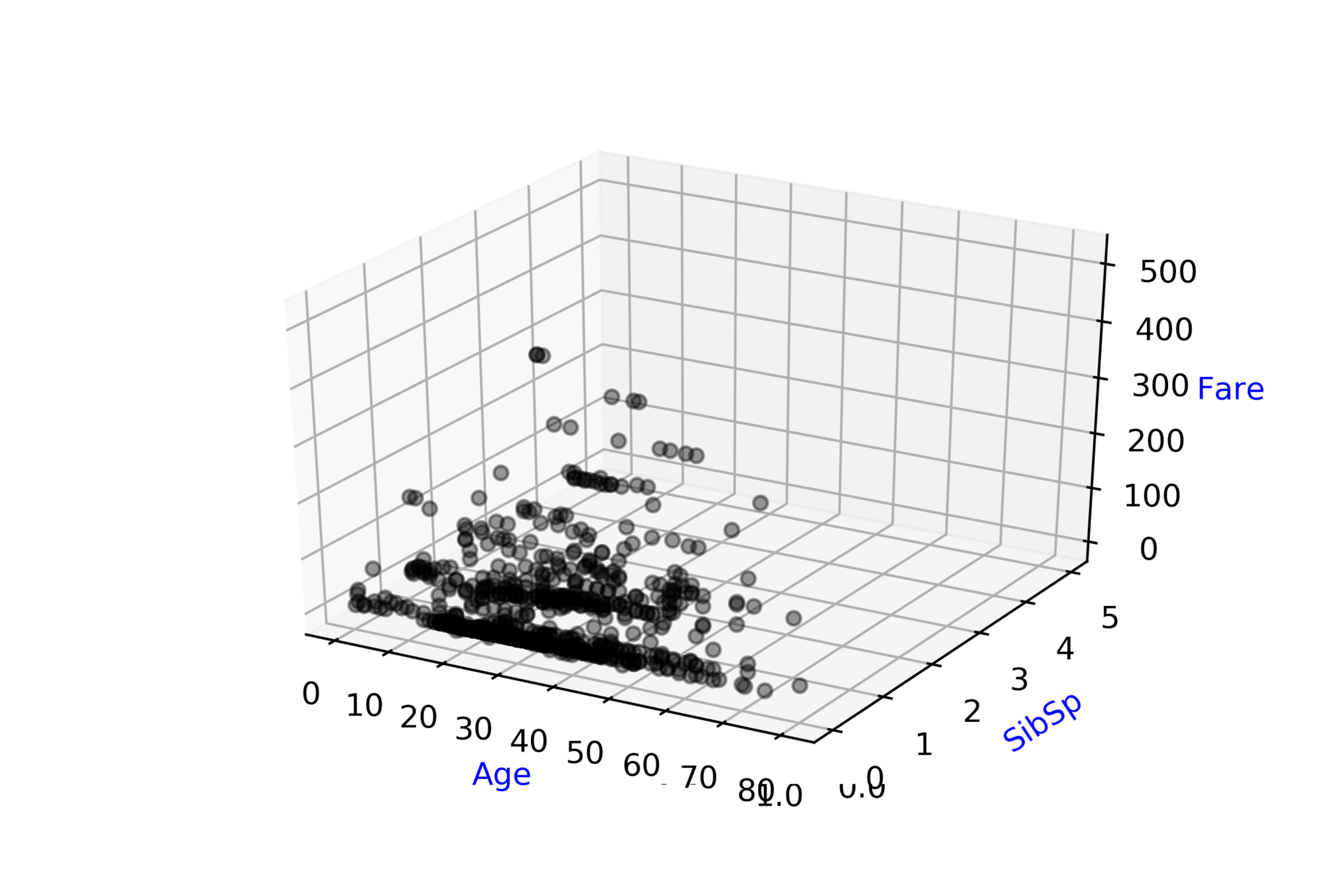
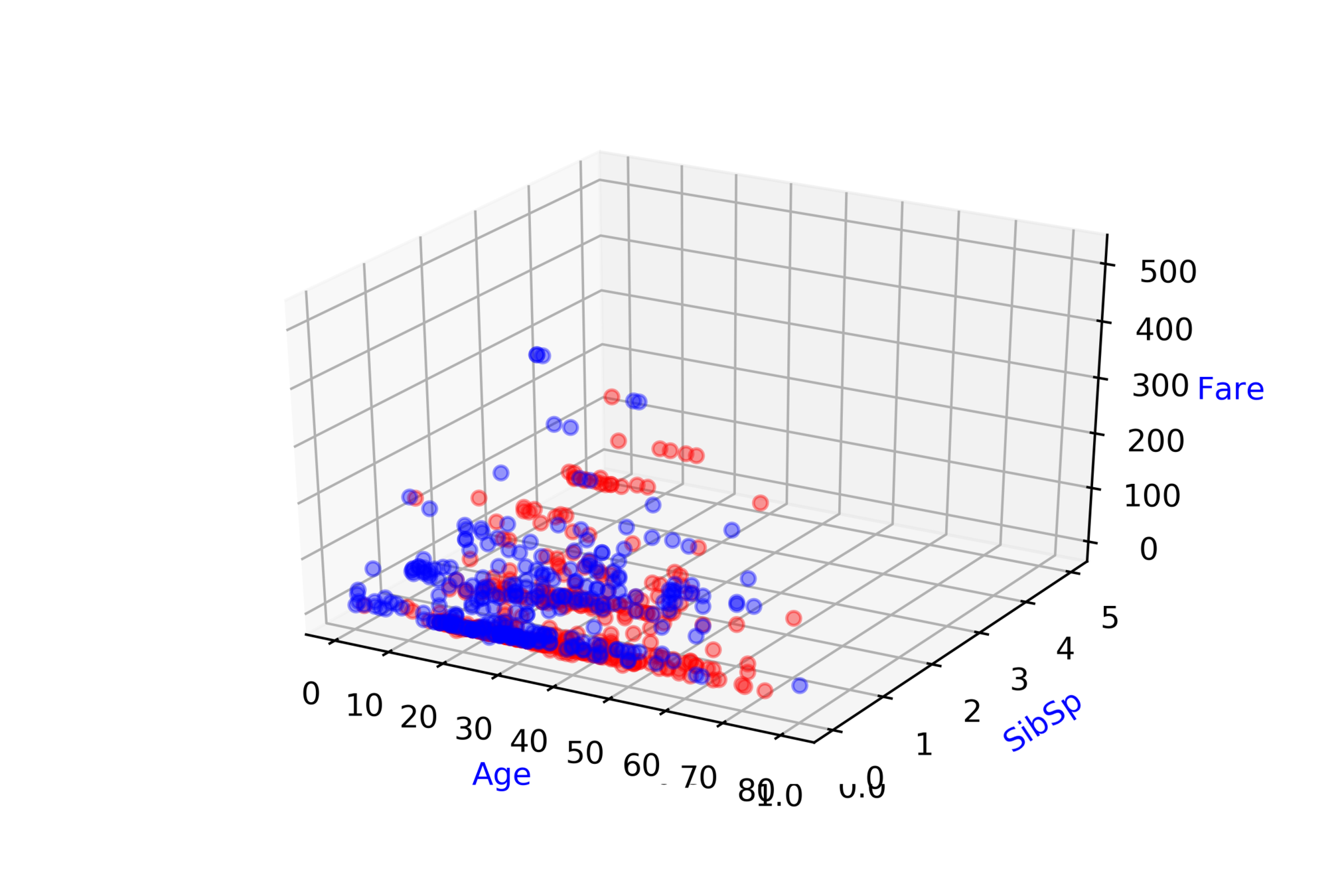
Modeling Complex Relations
How do we even come up with such complex functions ?
(c) One Fourth Labs

Class 1
Class 1
Class 1
Class 2
Class 2
Class 2
Class 1 : \( y^2 - x^2 + x^3/8 - y^3/6 > 0 \)
Class 2 : \( y^2 - x^2 + x^3/8 - y^3/6 \leq 0 \)
Class 1 : \( x^2*y + y^3*x > 0 \)
Class 2 : \( x^2*y + y^3*x \leq 0\)
Class 1: \( y - x*sin(x) > 0 \)
Class 2 : \( y - x*sin(x) \leq 0 \)
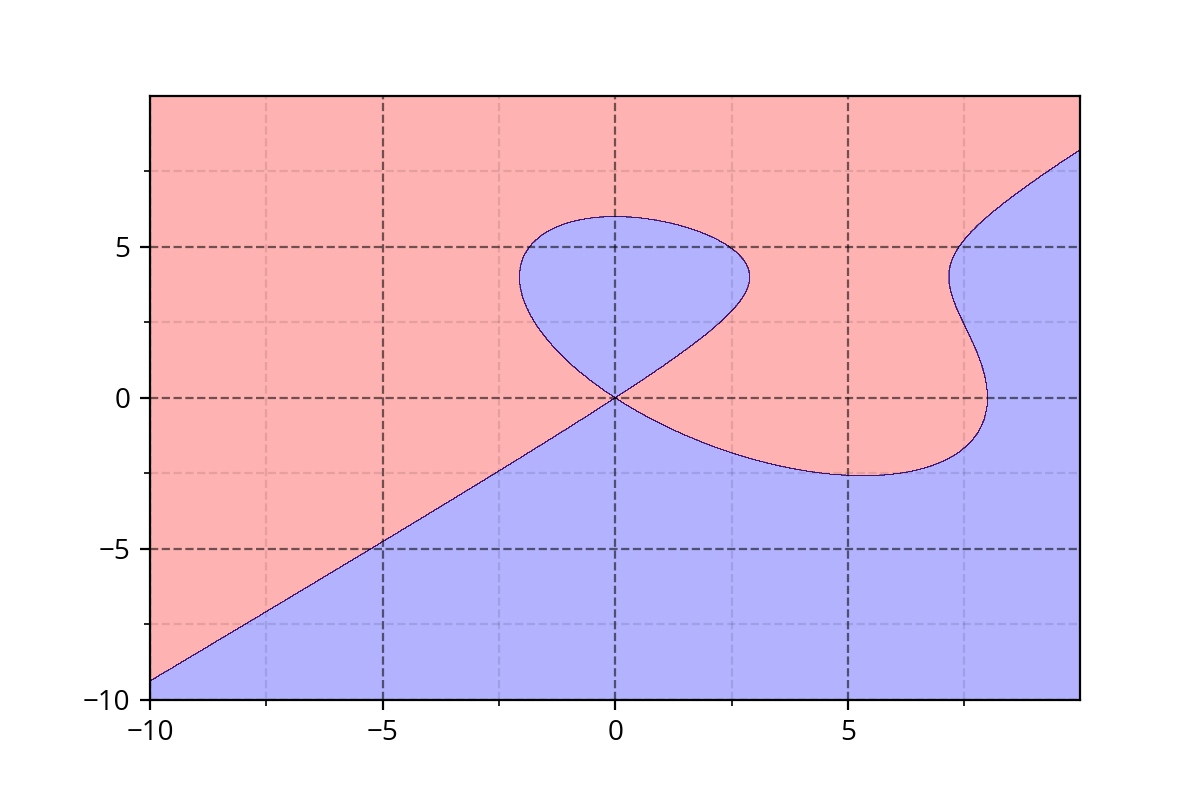
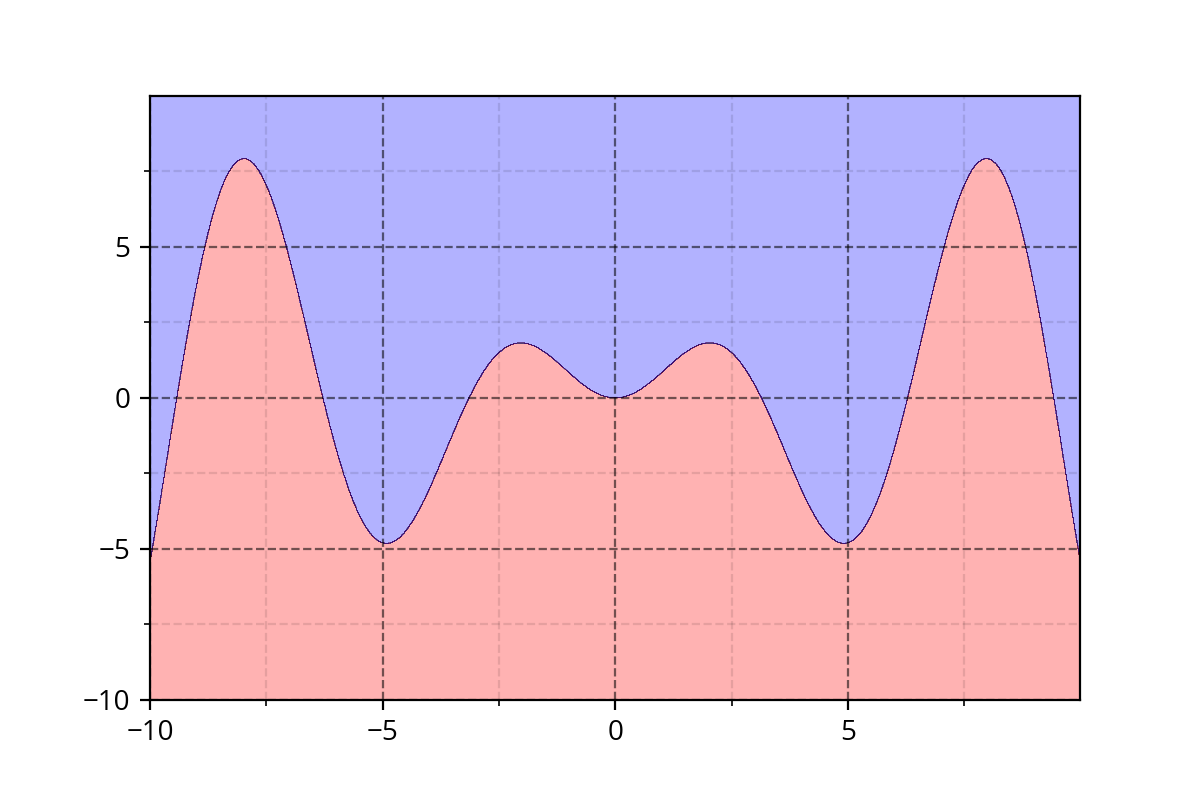
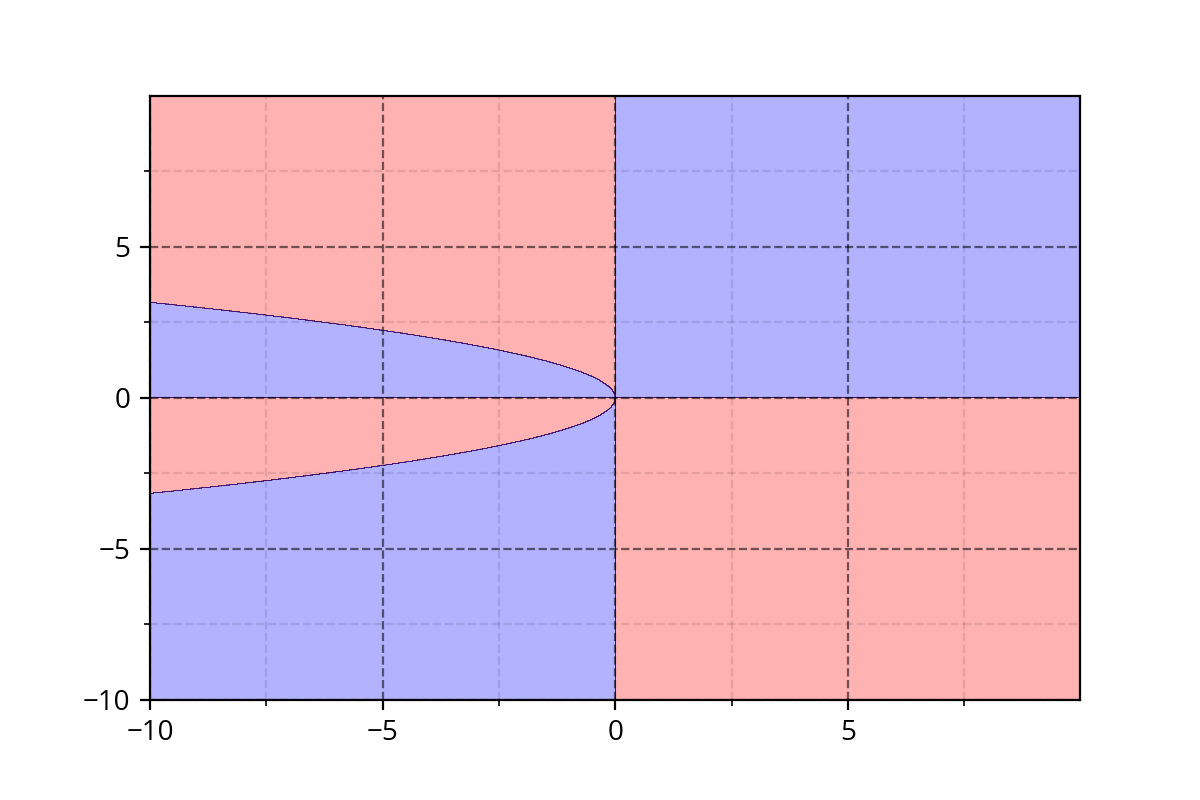
It's hard to come up with such functions. We need a simple approach!
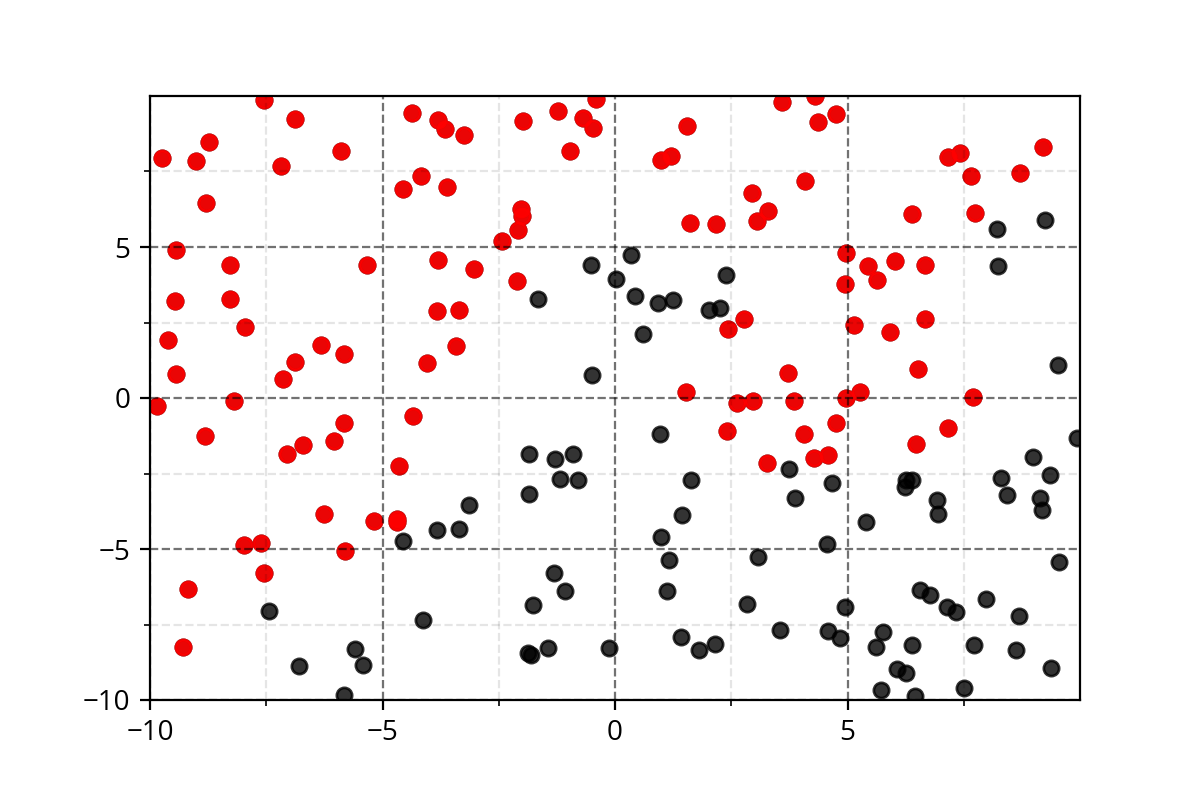
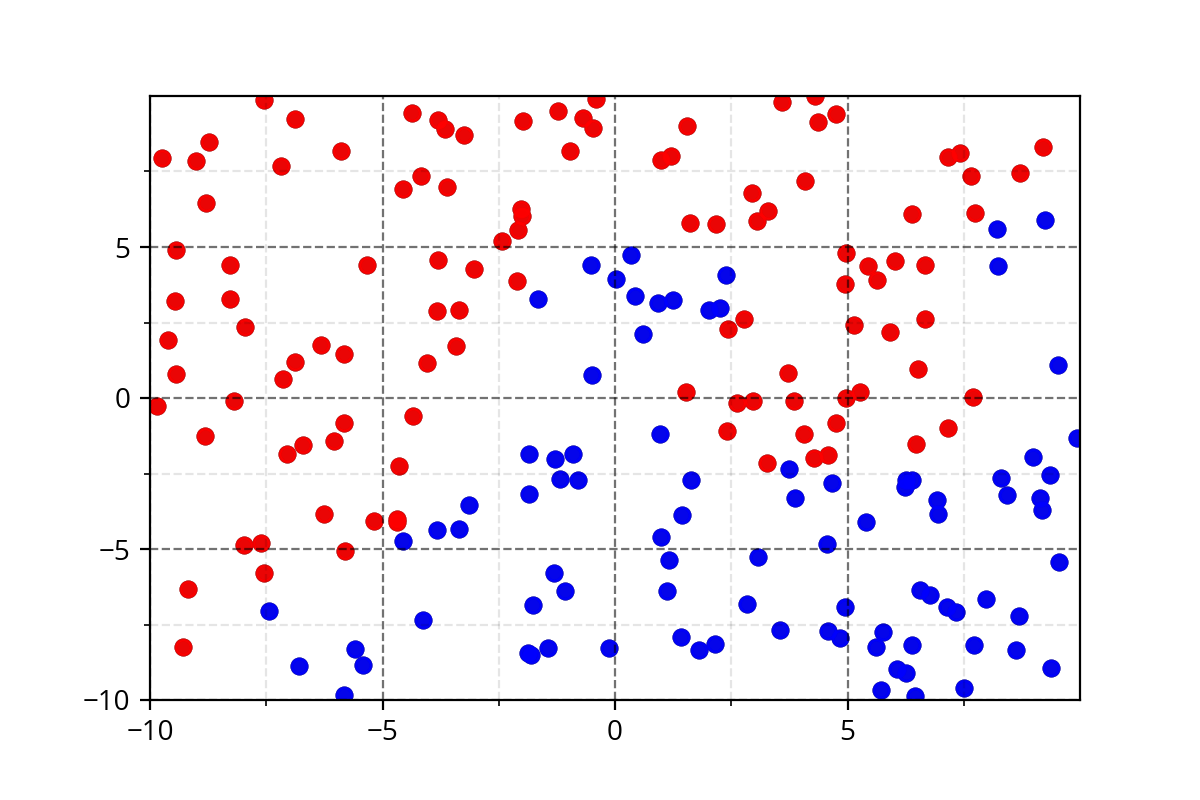
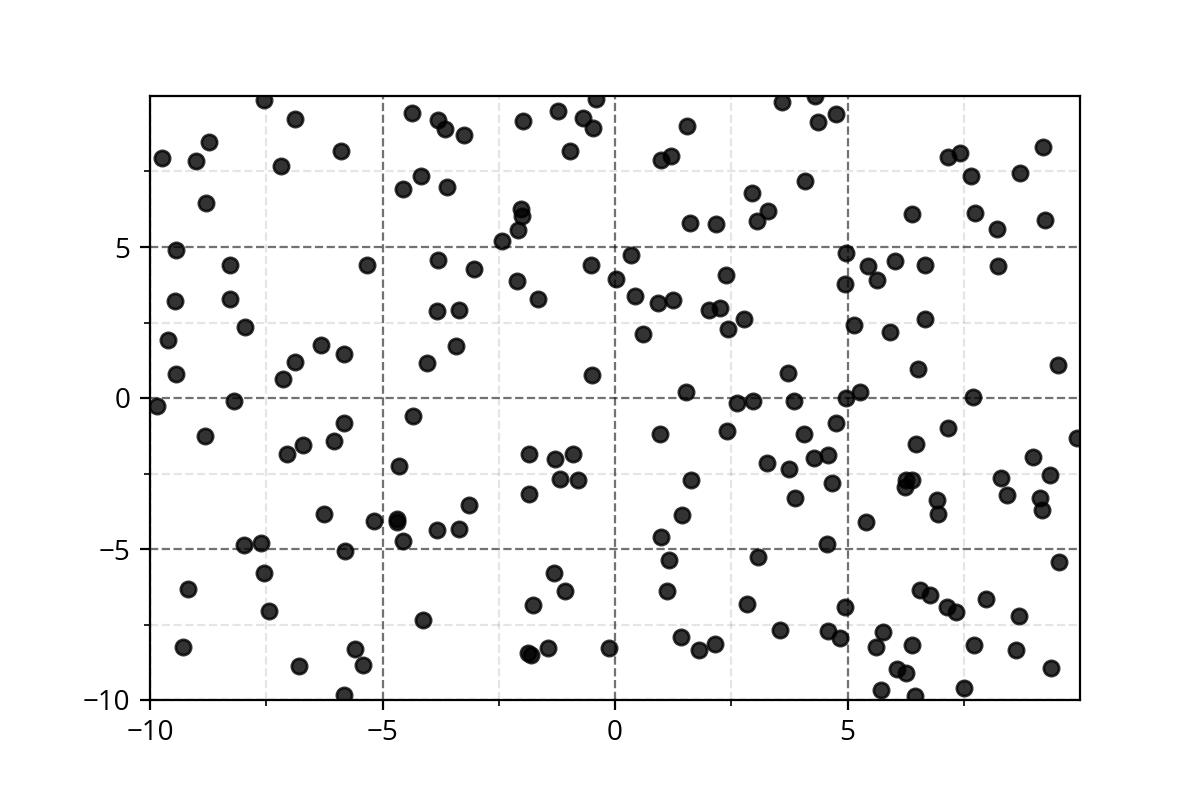
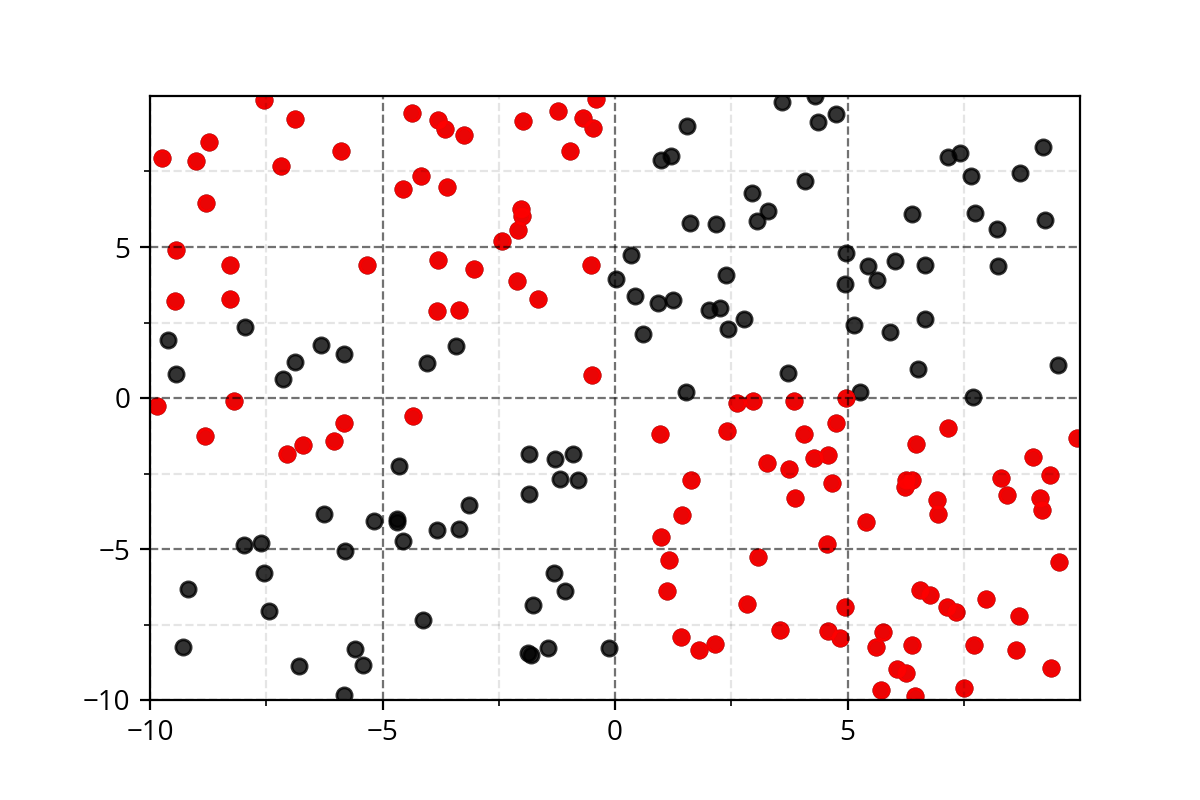
Modeling Complex Relations
How do we even come up with such complex functions ?
(c) One Fourth Labs

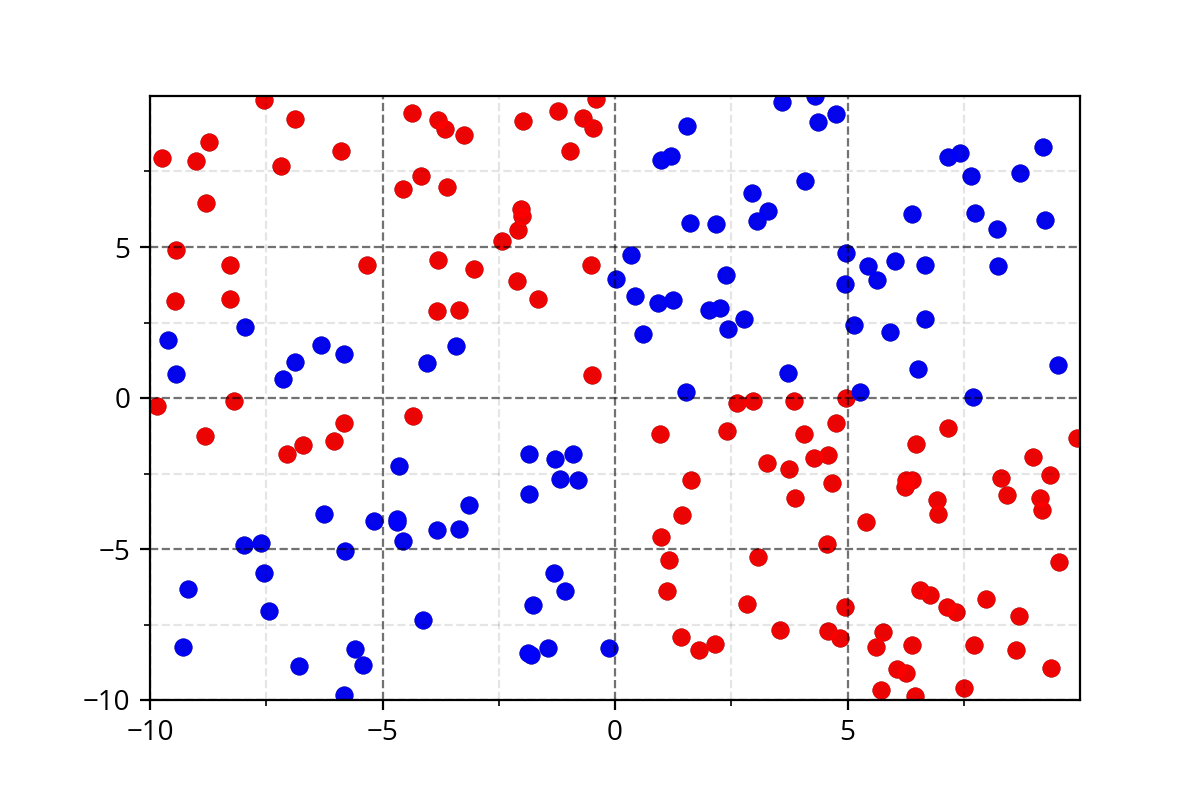
Class 1
Class 1
Class 1
Class 2
Class 2
Class 2
























































Modeling Complex Relations
How do we even come up with such complex functions ?

Class 1
Class 2

\( f(x_1,..,x_n) = \frac{1}{1+e^{-(w_1*x_1 + ... + w_n*x_n + b)}} \)
\( f(\bold{x},\bold{w}) = \frac{1}{1+e^{-(w*x + b)}} \)

\(w_1\)
\(w_n\)
\(x_n\)
\(x_1\)
\( f(\bold{x},\bold{w}) \)





\(x_1\)
\(x_n\)








\(\bold{h}\)


















Modeling Complex Relations
How do we even come up with such complex functions ?

Class 1
Class 1
Class 1
Class 2
Class 2
Class 2



\( f(x_1,..,x_n) = \frac{1}{1+e^{-(w_1*x_1 + ... + w_n*x_n + b)}} \equiv \)
\( f(\bold{x},\bold{w}) = \frac{1}{1+e^{-(w*x + b)}} \equiv \)






































(c) One Fourth Labs

















































Take-aways
How does all this connect to the six jars that we saw earlier ?
(c) One Fourth Labs

Show the 6 jars
1) Below data show a plot for non-linearly separable data
2) Below task show that you want to separate the blue points from red points
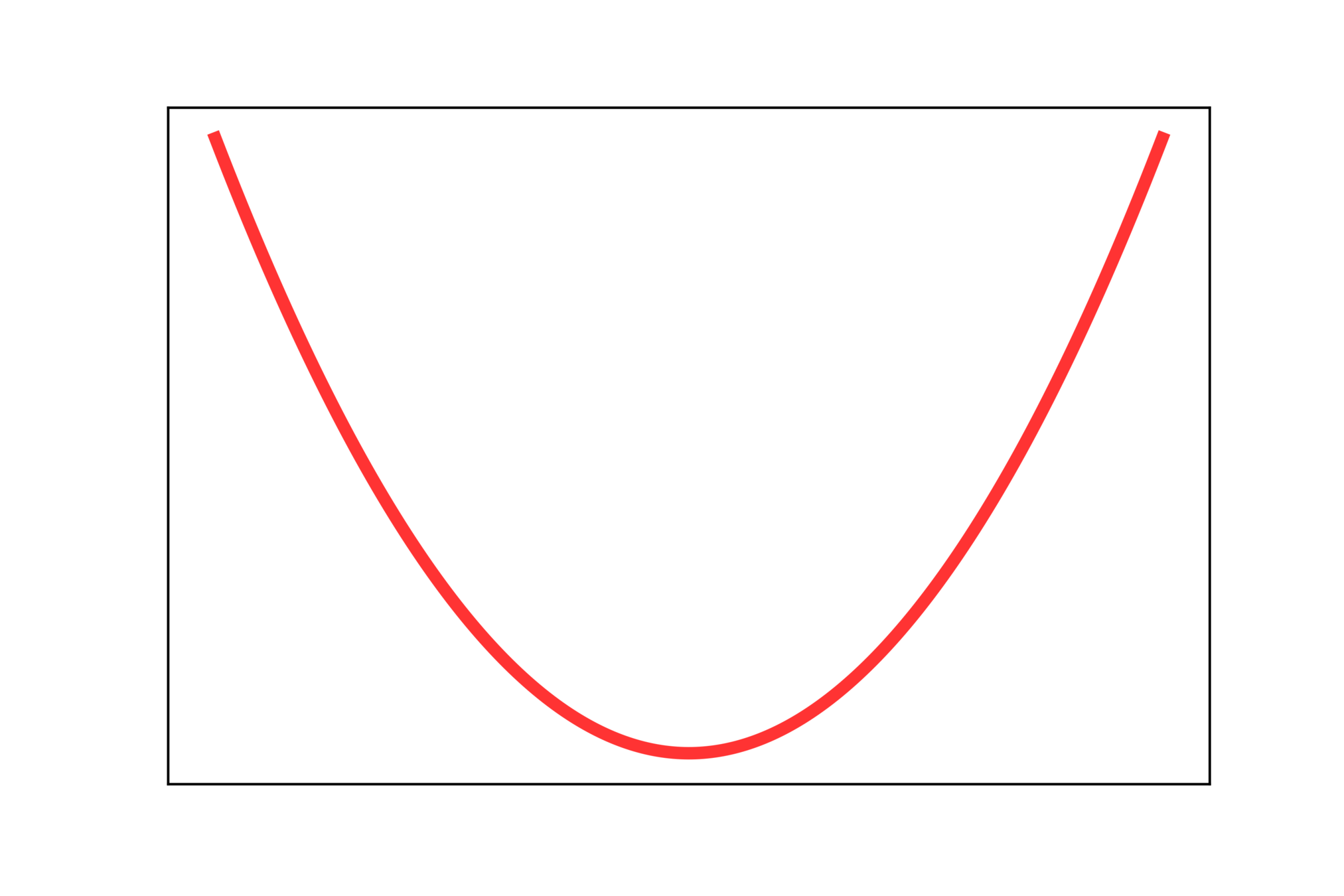
3) Below model show that you will be using a complex but smoooth function to do this
4) Below loss function show the curve for x^2 which is continuous
5) below learning algorithm show the update rule with derivatives
I will then give some commentary to connect all this
1. we care abt cntns functions
2. this slide (what is this function and what you are doing is essentially adjusting its parameters)
3. once again show that sigmoid cant do this
4. show how to project 3d data to 2d data
5. now take multiple datasets from kaggle and show their projections (in each case there would be a diff function fitting the data)
6.now show all the different functions that we had for different datasets. There is no way we can come up with these functions. what we know are basic functions but if we combine them we will get increasingly complex functions. lead upto UAT
7. also show how you can always model simple relation using complex functions (need a demo for this)
8. show summary slide connecting data task model and learning algo (we are going to see a family of complex functions)
Take-aways
How to distribute your work through the six jars?
(c) One Fourth Labs


\( \in \mathbb{R} \)

Loss
Model
Data
Task
Evaluation
Learning
Real inputs
\( w = w + \eta \frac{\partial L}{\partial w} \)
\( b = b + \eta \frac{\partial L}{\partial b} \)
Classification
Take-aways
What was all this leading up to ?
(c) One Fourth Labs

Show the 6 jars
1) On LHS Show one sigmoid neuron
2) Now add one more neuron, then one more and so on to make the ground floor (basically slowly build the fully connected neural network)
Take-aways
What was all this leading up to ?
(c) One Fourth Labs

Accuracy
Data




\( w = w + \eta \frac{\partial L}{\partial w} \)
\( b = b + \eta \frac{\partial L}{\partial b} \)















Task

Model

Loss

Learning

Evaluation
Copy of 1.8 Final Draft
By preksha nema
Copy of 1.8 Final Draft
- 1,223



