1.9 Multilayered Network of Neurons
Your first Deep Neural Network

Learning Algorithm
Forward Propogation

\(a_1 = W_1*x + b_1 = [ -2.2 -0.1 5.3 ]\)
\(h_1 = tanh(a_1) = [ -0.97 -0.1 0.99 ]\)
\(a_2 = W_2*h_1 + b_2 = [ 0.41 -0.24 1.24 ]\)
Output :
\(L(\Theta) = -\text{log}\hat{y_l} = 0.43 \)
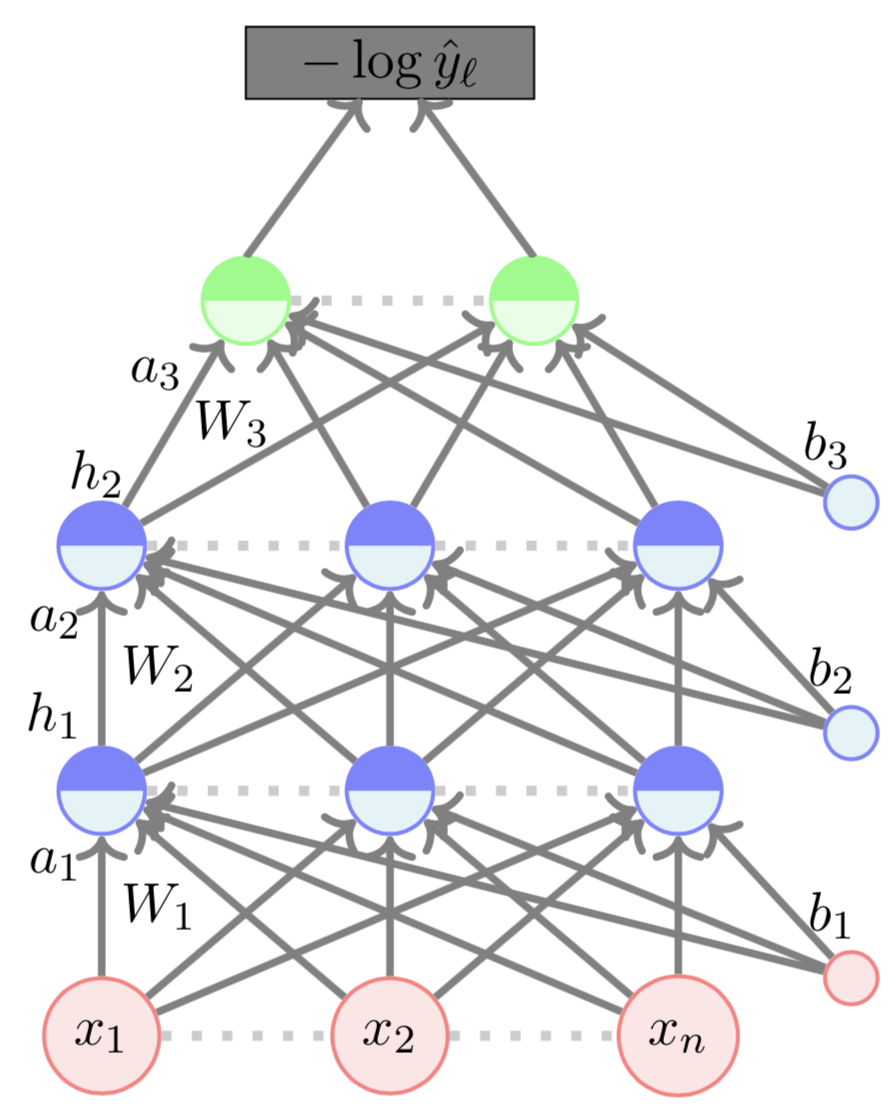
\(h_2 = tanh(a_2) = [ 0.39 -0.24 0.84 ]\)
\(a_3 = W_3 * h_2 + b_3 = [ 0.01 -0.58 ]\)
\(\hat{y} = softmax(a_3) = [ 0.64 0.36 ]\)
Learning Algorithm
Backward Propogation

\( \nabla_{a_L} \mathscr{L}(\theta)\) :
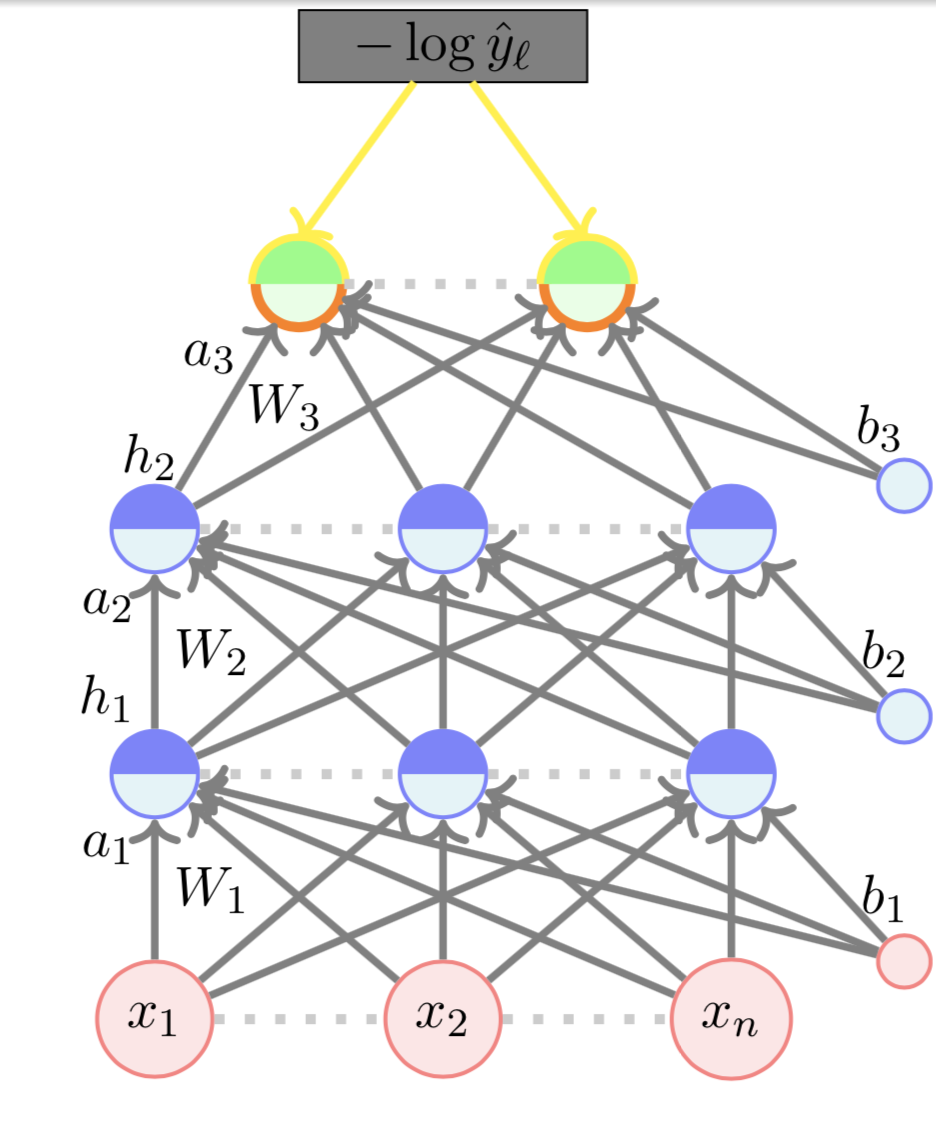
Learning Algorithm
Backward Propogation

\( \nabla_{h_2} \mathscr{L}(\theta)\) :
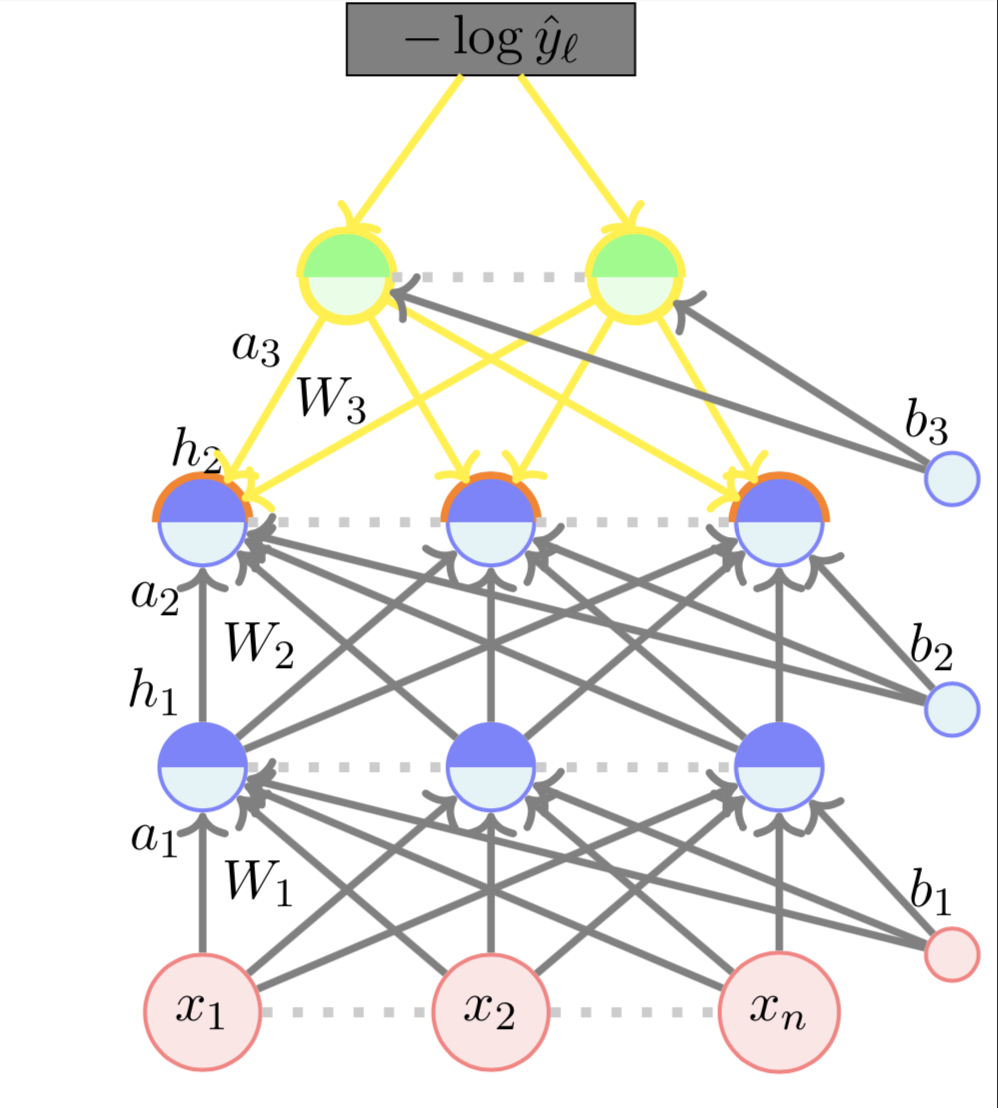
\( \nabla_{a_3} \mathscr{L}(\theta)\) :
Learning Algorithm
Backward Propogation

\( \nabla_{a_2} \mathscr{L}(\theta)\) :
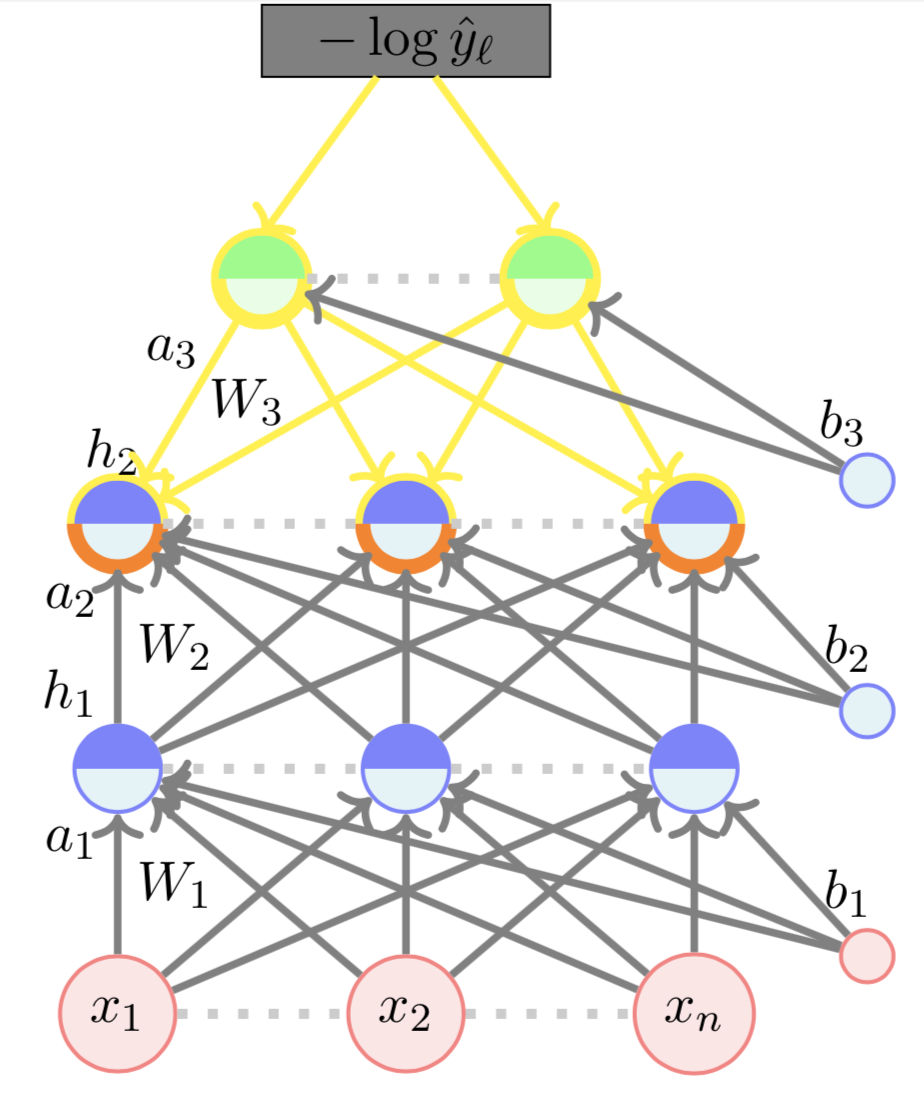
\( \nabla_{h_2} \mathscr{L}(\theta)\) :
Learning Algorithm
Backward Propogation

\( \nabla_{W_2} \mathscr{L}(\theta)\) :
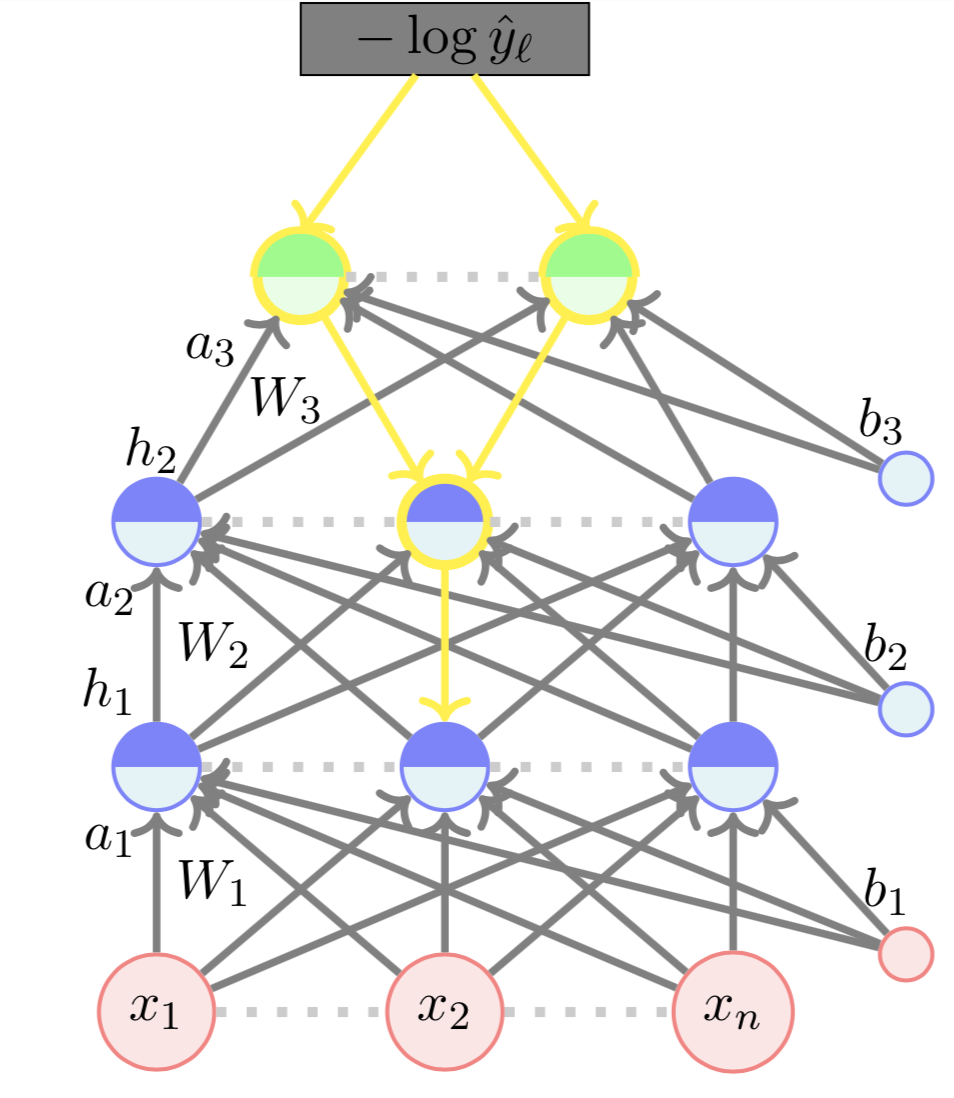
\( \nabla_{a_2} \mathscr{L}(\theta)\)
Learning Algorithm
Backward Propogation

\( \nabla_{b_2} \mathscr{L}(\theta)\) :
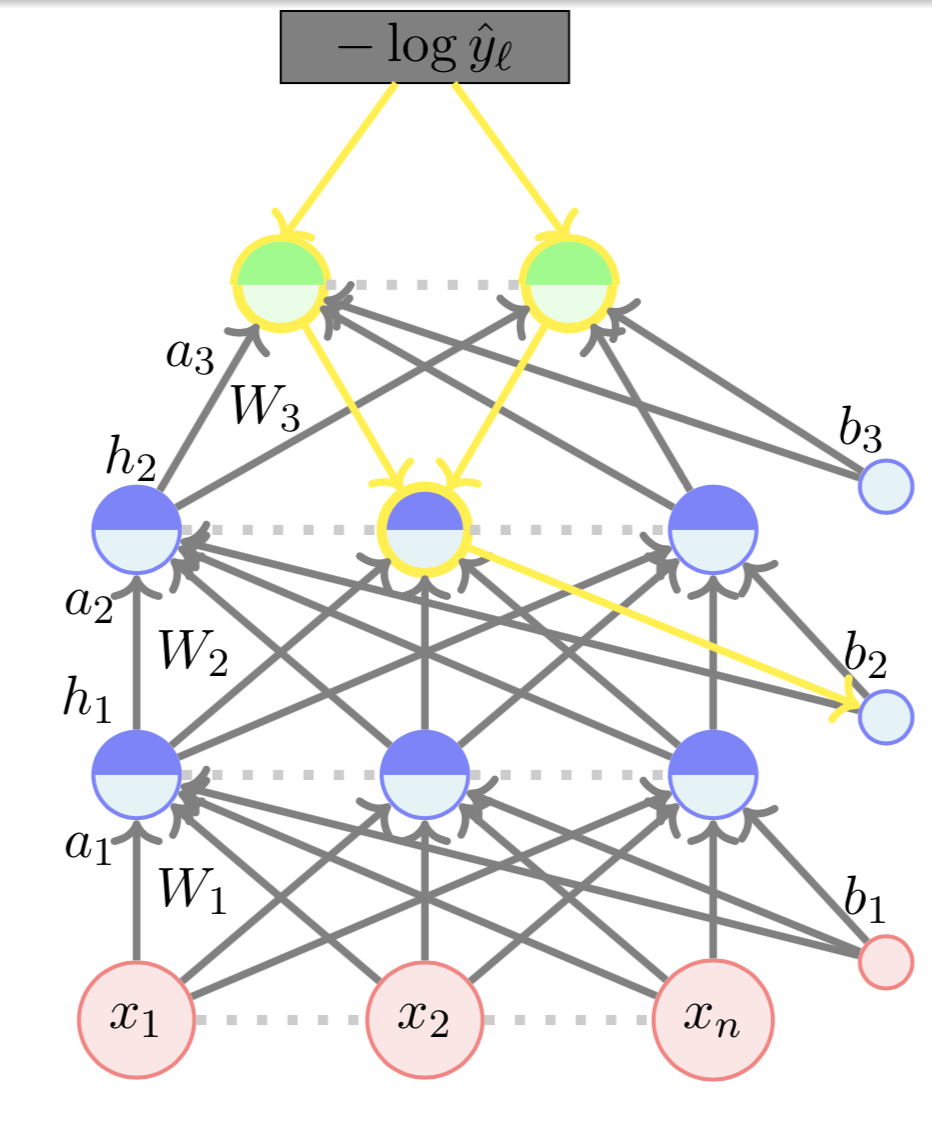
\( \nabla_{a_2} \mathscr{L}(\theta)\)
Evaluation
How do you check the performance of a deep neural network?
(c) One Fourth Labs

Test Data
Indian Liver Patient Records \(^{*}\)
- whether person needs to be diagnosed or not ?
| Age |
| 65 |
| 62 |
| 20 |
| 84 |
| Albumin |
| 3.3 |
| 3.2 |
| 4 |
| 3.2 |
| T_Bilirubin |
| 0.7 |
| 10.9 |
| 1.1 |
| 0.7 |
| y |
| 0 |
| 0 |
| 1 |
| 1 |
.
.
.
| Predicted |
| 0 |
| 1 |
| 1 |
| 0 |
Take-aways
What are the new things that we learned in this module ?
(c) One Fourth Labs

\( x_i \in \mathbb{R} \)


Loss
Model
Data
Task
Evaluation
Learning
Real inputs
Tasks with Real Inputs and Real Outputs
Back-propagation
Squared Error Loss :
Cross Entropy Loss:
Copy of Working Example
By preksha nema
Copy of Working Example
- 760



