1.10 Vectors and Matrices
What are they and why to we care about them ?

Vectors
What are they ?
(c) One Fourth Labs

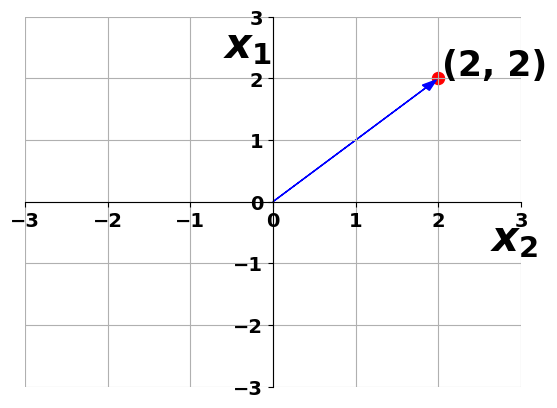

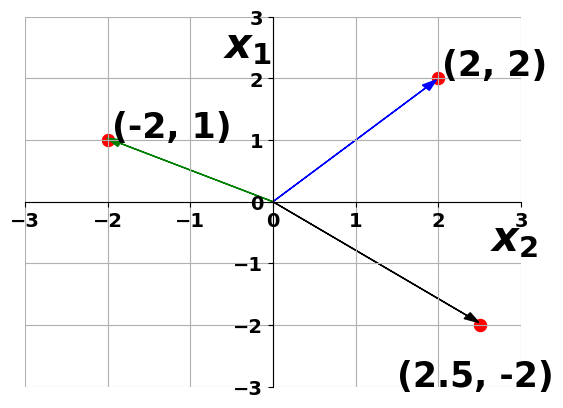
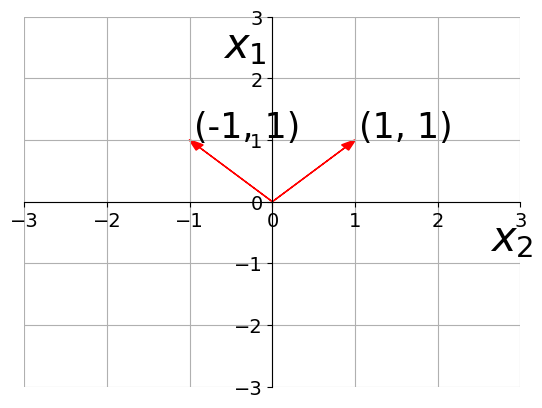
- Magnitude of a vector
- Direction of a vector
Magnitude of a vector
Magnitude of (2,2)
Magnitude of (-2,1)
Magnitude of (2.5,-2)
Magnitude of (1,1)
Magnitude of (-1,1)
Vectors
What are they ? (some jargon)
(c) One Fourth Labs

Euclidean Space
In geometry, a two- or three-dimensional space in which the axioms and postulates of Euclidean geometry apply is a Euclidean space. A space in any finite number of dimensions, in which points are designated by coordinates (one for each dimension) and the distance between two points is given by a distance formula.
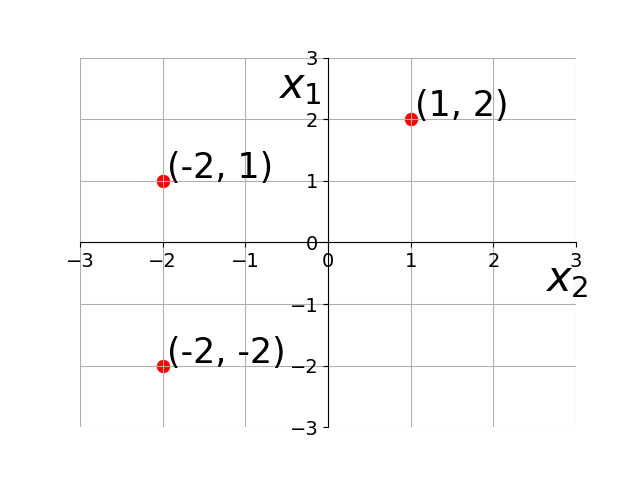
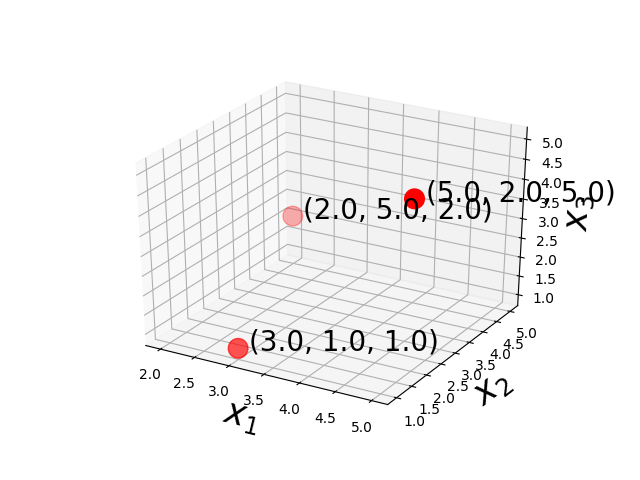
2D Euclidean Space
3D Euclidean Space
In geometry, a two- or three-dimensional space in which the axioms and postulates of Euclidean geometry apply is a Euclidean space. A space in any finite number of dimensions, in which points are designated by coordinates (one for each dimension) and the distance between two points is given by a distance formula. L2 Norm is also called Euclidean norm.
In geometry, a two- or three-dimensional space in which the axioms and postulates of Euclidean geometry apply is a Euclidean space. A space in any finite number of dimensions, in which points are designated by coordinates (one for each dimension) and the distance between two points is given by a distance formula
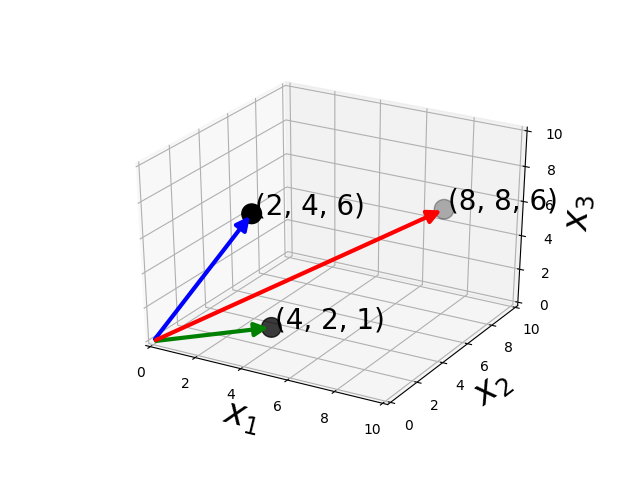
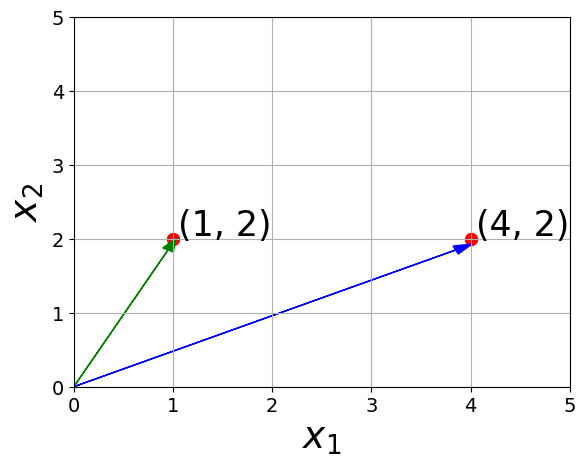
Vectors
How do you add two vectors ?
(c) One Fourth Labs

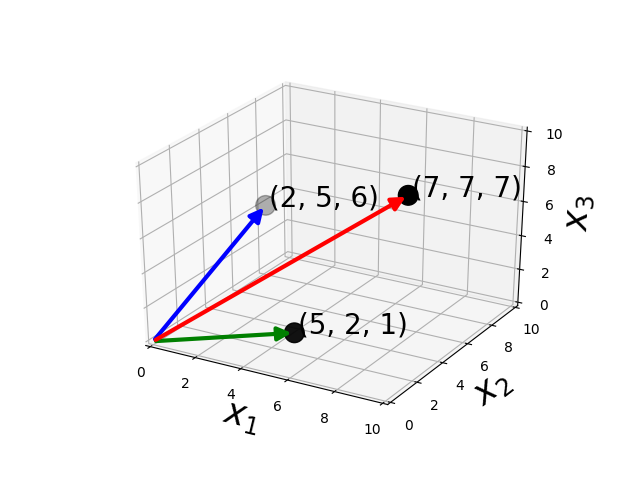
Addition
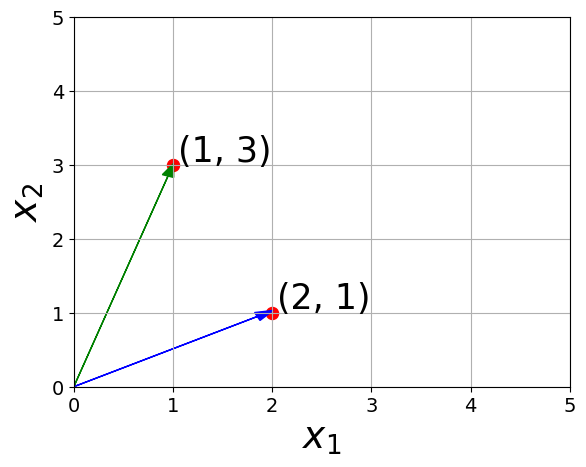
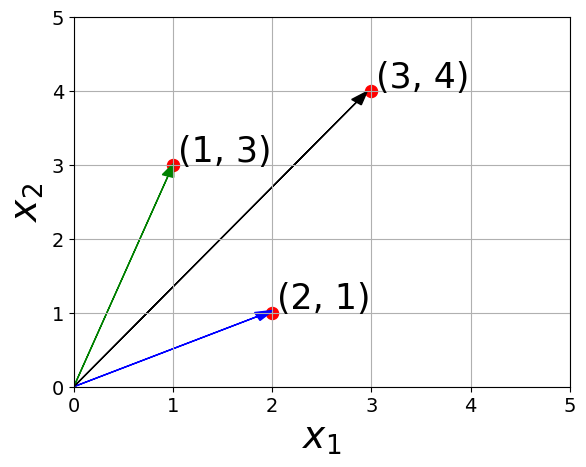
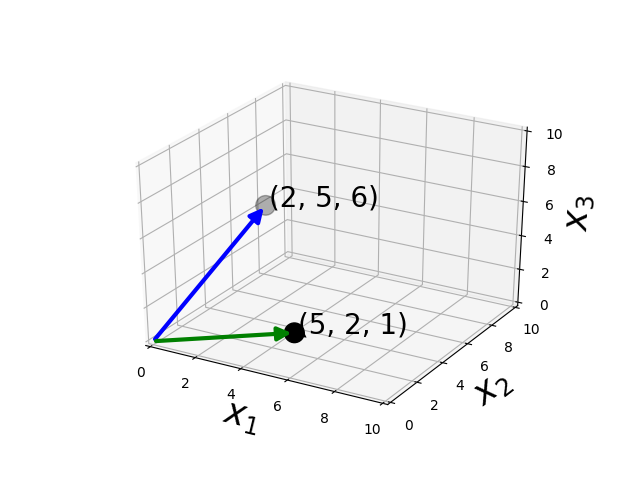
Addition


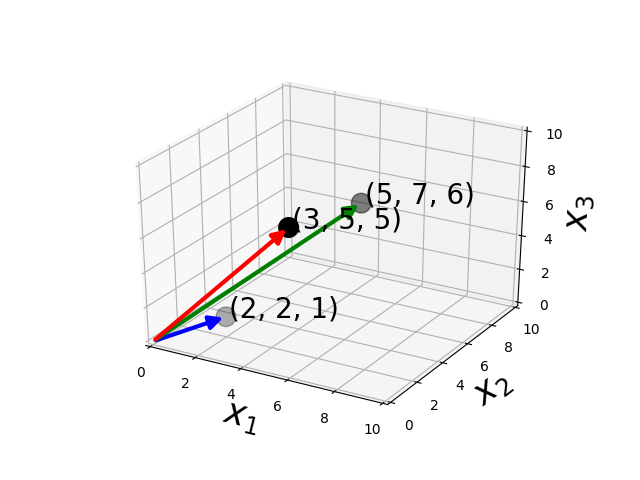
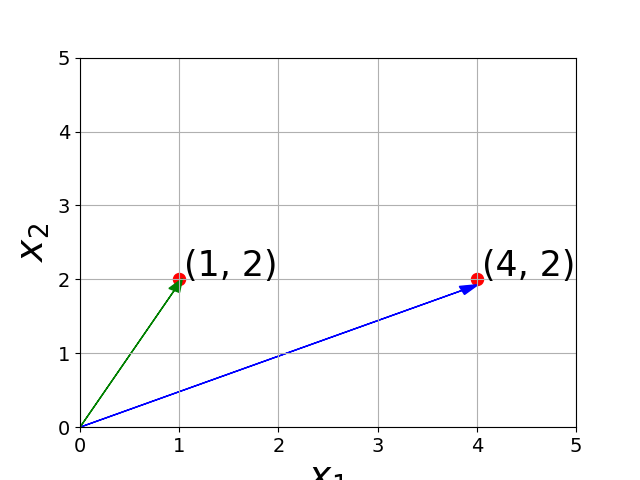
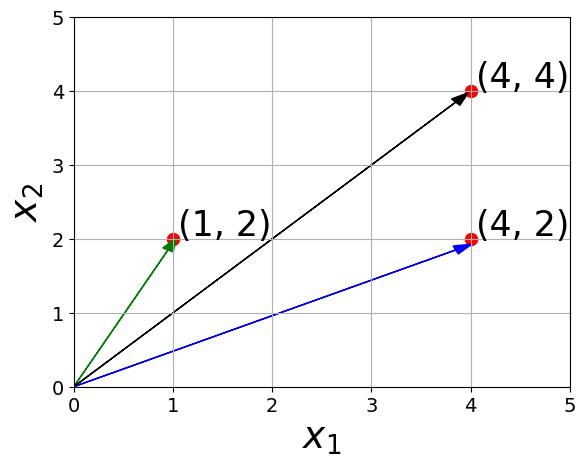
Vectors
How do you subtract two vectors ?
(c) One Fourth Labs

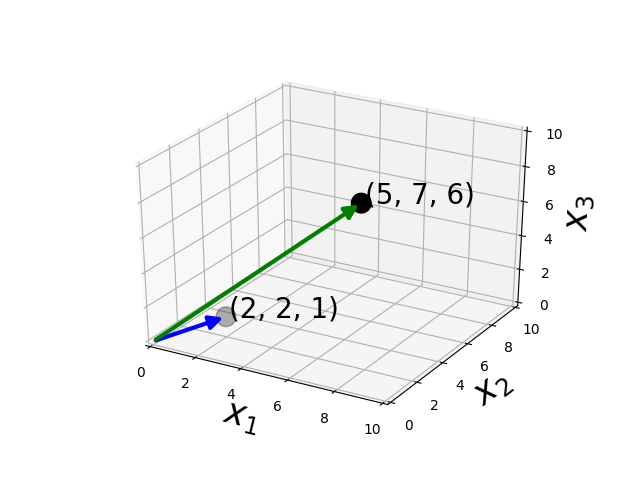
Subtraction

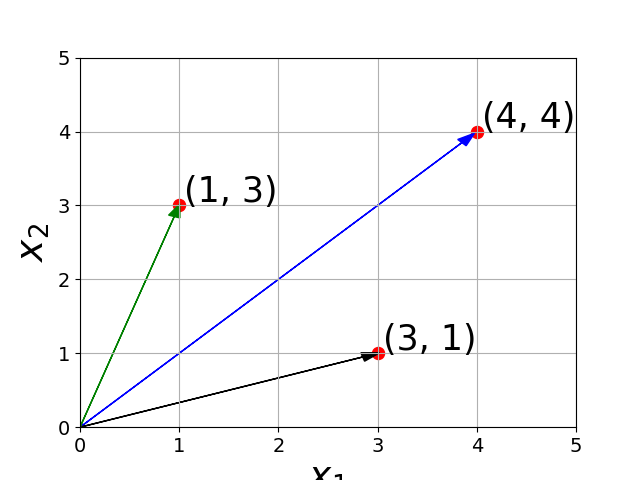
Subtraction


Vectors
How do you subtract two vectors ?
(c) One Fourth Labs

Subtraction

Subtraction



Vectors
How do you multiply two vectors ?
(c) One Fourth Labs

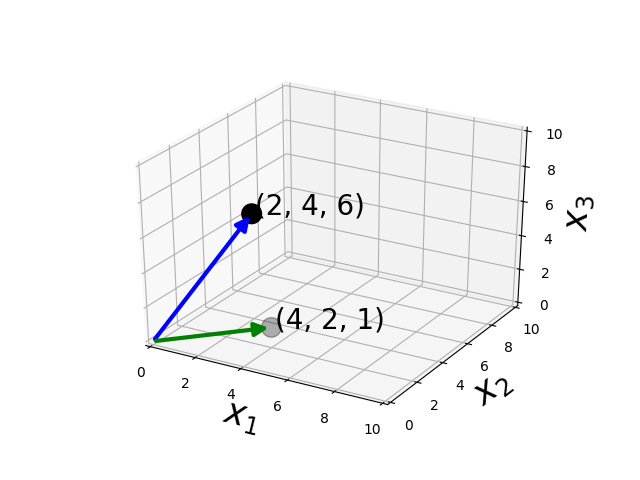
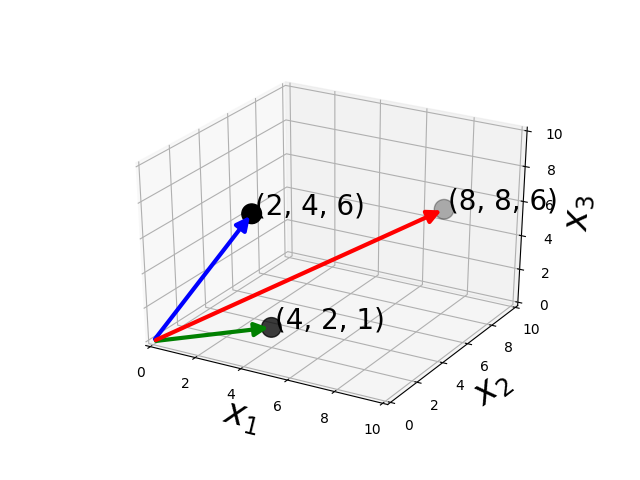



Multiplication - Dot product
Multiplication - Dot product
Vectors
How do you project a vector onto another ?
(c) One Fourth Labs

Slide1:
- Same as this video upto 4:09 seconds (but change the vectors a bit
https://www.youtube.com/watch?v=fqPiDICPkj8
- Now take a numeric example in 2d and compute
- Now take a numeric example in 3d and compute
- Now give formula for n-dimensions
Vectors
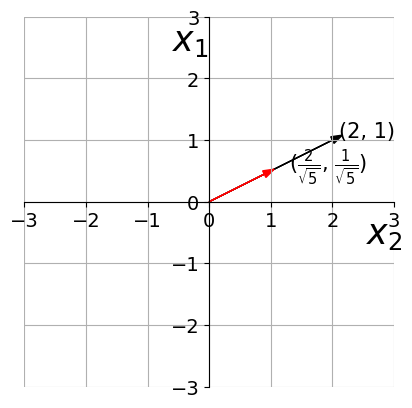
What is a unit vector ?
(c) One Fourth Labs

Any vector whose magnitude is 1?
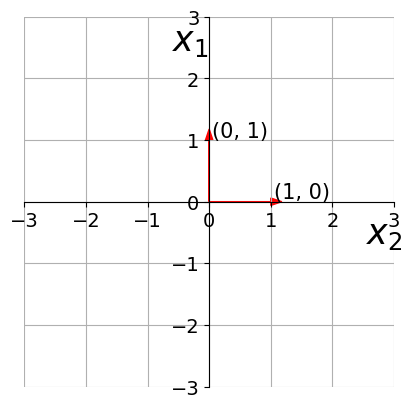
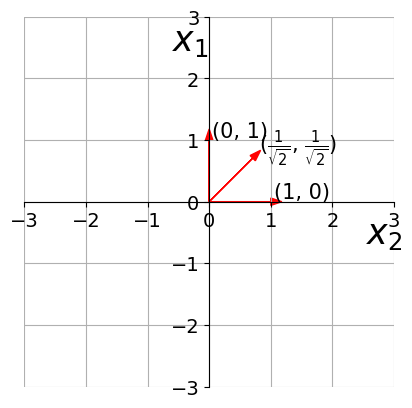
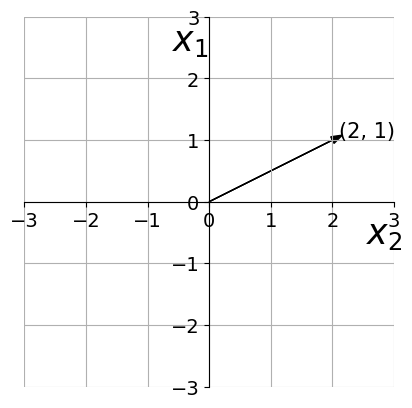
To obtain the unit vector in the direction of a non-unit vector, divide by the magnitude of the given vector.
Vectors
How do you compute the angle between two vectors ?
(c) One Fourth Labs

- 2d vector on LHS, cos formula on RHS, computations
- 3d vector on LHS, cos formula on RHS, computations
Vectors
What are orthogonal vectors?
(c) One Fourth Labs

Show cos formula on RHS
- Orthogonal --> perpendicular --> \theta = 90 --> cos = 0 --> cosine_formula = 0 --> dot product = 0
- Show examples of 2d orthogonal vectors. First show column vectors, then compute dot product, show it is 0, then show the vectors on the plot to convey that they are indeed 0.
- Repeat point 2 with examples in 3d
- Now show one example in 5d (its okay if you need to spread this across more than 1 slide)
Vectors
Why do we care about them ?
(c) One Fourth Labs

- Show an icon of a mobile phone. Now adjacent to this icons show one row containing specs of this phone (the idea is to show that all data that we encounter can be viewed as vectors) - the black boxes will be replaced by icons
- Show an icon of a customer. Now adjacent to this icon show one row containing details of this customer
- Show an icon of an MNIST digit and then show a vector
in each of the above case mention the dimension of the vector as R^?
Matrices
What are they ?
(c) One Fourth Labs

- Start with a vector and stack more vectors to form a matrix
- Highlight one column and show that this is a column vector
- Highlight one row and show that this is a row vector
Matrices
How do you add two matrices ?
(c) One Fourth Labs

- Show two matrices and show how the addition happens element-wise
Matrices
How do you multiply a matrix with a vector ?
(c) One Fourth Labs

- Show a 2 x2 vector and multiply it with a 2x1 vector, show the formula for how you compute each element of the resulting vector. Show the corresponding animation also (highlight first row of the matrix and the vector, then the second row of the matrix and the vector)
- Now show the geometric interpretation of this (same as slide 3 lecture 6 from CS7015).
- Repeat the same for a 3 x3 matrix
- Now try multiplying a 3x3 matrix with a 2x1 vector. Show how this is not possible because there are 3 terms in the matrix and only two in the vector.
- Now try multiplying a 2x3 matrix with a 3x1 vector. This is possible. This results in the conclusion that the number of columns in the matrix should be the same as the number of rows in the vector.
For showing illegal use this icon
Matrices
How do you multiply two matrices ?
(c) One Fourth Labs

- Show two 3x3 matrices. Show the multiplication one column at a time (i.e., the matrix A first gets multiplied with the first column of matrix B, then next column and so on, similar animations as on the previous slide)
- Now try a 3x3 matrix with a 2x3 matrix. Show that you need to multiply the matrix A with the columns of B. Now this is not possible as we already saw on the previous slide.
- Try 3x2 with 2 x4 and show this is possible
- In general, m x k can be multiplied with kxn to get m x n output
Matrices
Is there an alternate way of multiplying matrices ?
(c) One Fourth Labs

- Show a 2x2 matrix with a 2 x1 vector say a11, a12, a21, a22 and b11, b21. Show the output as a11*b11 + a12* b21, a21*b11 + a22* b21. Now rewrite it as b11*[a11, a21] + b21*[a11, a21] (everything as column vectors not row vectors)
- Show a 2x2 matrix with a 2 x2 matrix. Repeat the same story as above where the first column of the output is the linear combination of the the columns if A and similar second column.....
Matrices
What is the common operation that you will see in this course ?
(c) One Fourth Labs

- Show Wx + b in very big font
- Using an arrow point to W and write R^{mxn}
- [Now I will ask them the dimensions of x and b so pause]
- Now write the dimension of x
- Now write the dimension of b
Matrices
Why do we care about them ?
(c) One Fourth Labs

- Show an icon of a mobile phone. Now adjacent to this icons show one row containing specs of this phone
- Now below this show icons for multiple phones and there corresponding data so that we get a matrix
- Repeat the above by replacing phones by different MNIST digits.
Text
Copy of Copy of 1.10 Vectors and Matrices
By preksha nema
Copy of Copy of 1.10 Vectors and Matrices
matrices
- 643



