Dynamic Programming
Introduction to dynamic programming
what is the result of
1+1+1+1+1+1+1+1
Answer is Eight
If we add another +1 to the expression above the output is Nine
We are able to calculate faster for additional +1 because we memorized the previous result
So In dynamic programming we remember stuff to save time later
If you have sloved a problem with given input than save the result for future reference to avoid solving the same problem again and again
Essence of Dynamic Programming
Components of Dynamic Programming
- Recursion
- Memoization
Characteristics of Dynamic Programming
- Optimal Substructure property
- A given problem has optimal substructure property, If an Optimal solution of the given problem can be obtained by using the optimal solution of its subproblems.
- fib(n) = fib(n-1) + fib(n-2) if n>1
- Overlapping Subproblems
- Subproblems are a subset of the original problem. Any problem has overlapping subproblems, if finding its solution requires solving the same problem again and again.
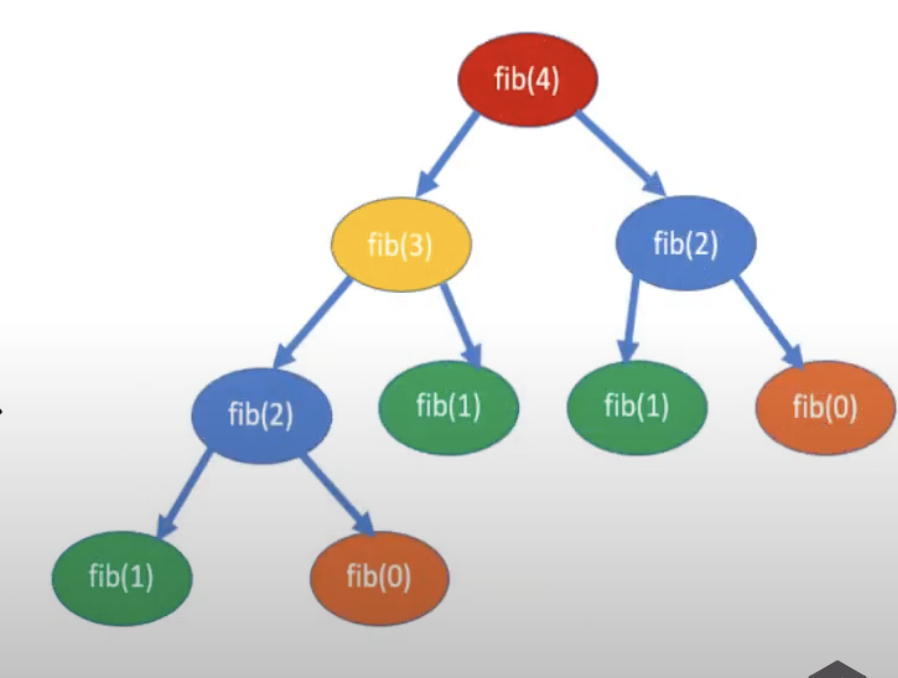
Overlapping sub problems
Dynamic Programming Methods
- Top-down (Memoization)
- It is similar approach to recursion as it looks for value in the table first which acts as a cache before computing solutions.
- If the solution is found than the result will be taken otherwise the problem will be solved and result is stored for the future use.
- Bottom-up (Tabulation)
- Tabulation is the opposite of top-down approach and avoids recursion
- In this approach we solve the problem in bottom up manner by solving all the related sub problems first.
Technique to Solve DP problems
- To solve a dynamic problem we ca use the fast method
- Find a recursive solution
- Analyse the solution (Look for overlapping problems)
- Save the result for future (Use array for caching purpose)
- Tweek the solution to make it more powerful by eliminating recursion overhead. (Known as bottom up approach)
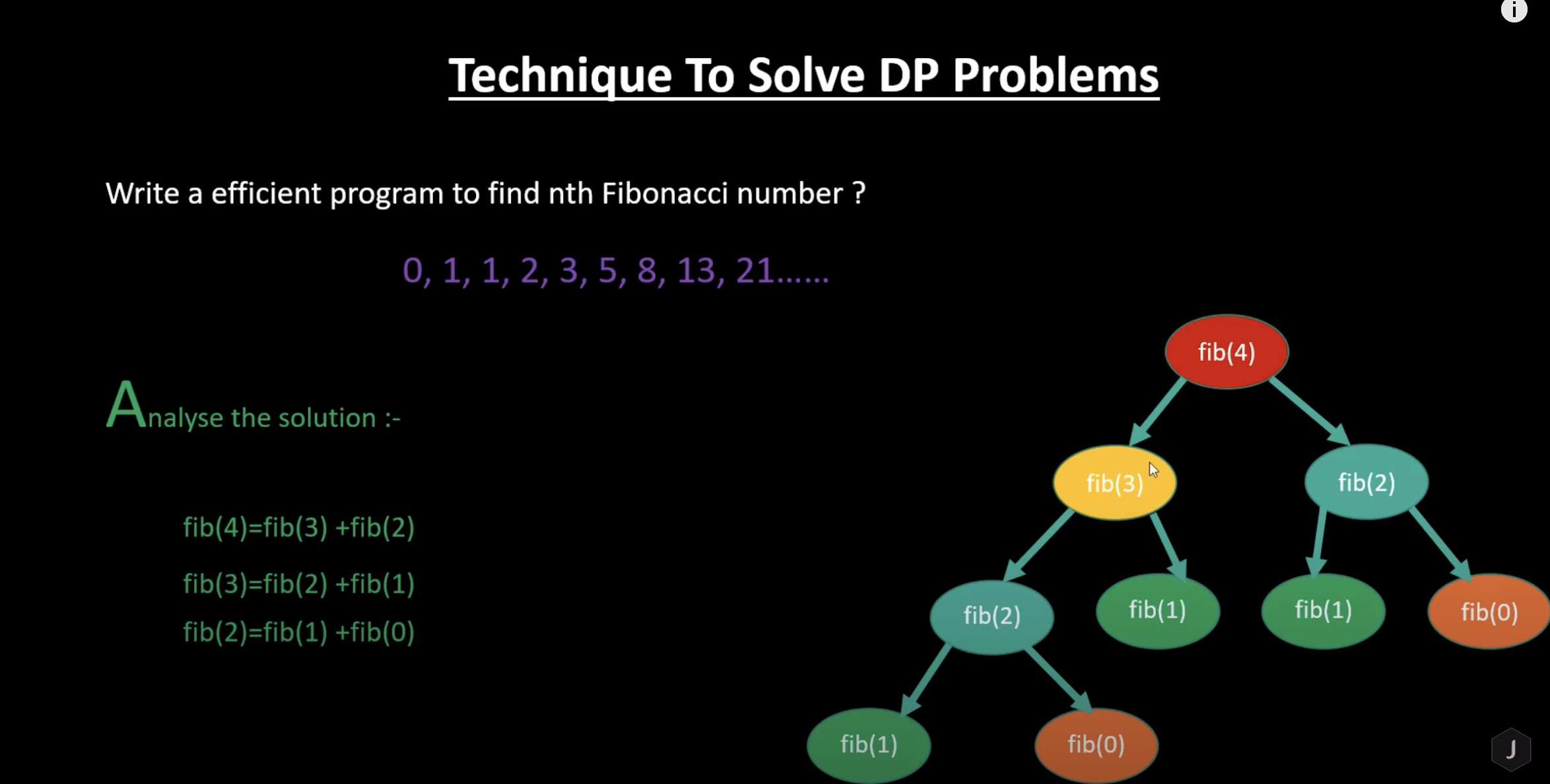
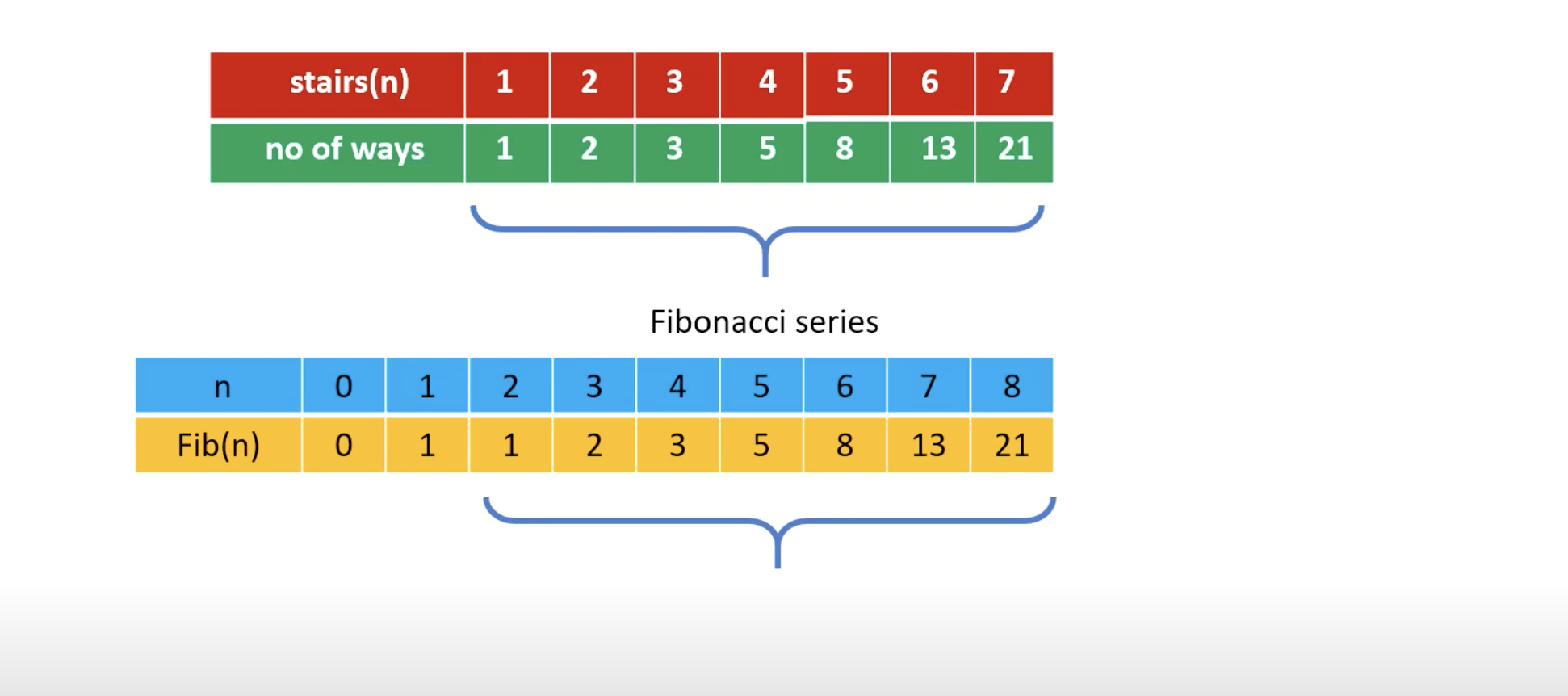
Fibonacci number
Write an efficient program to find nth Fibonacci number ?
- a fibonacci series looks like 0,1,1,2,3,5,8,13,21....
Recursive Solution
public static int fib(int n) {
if (n < 2)
return n;
return fib(n - 1) + fib(n - 2);
}Memoization in recursive solution
public static int fib(int n, int[] cache) {
if (n < 2) {
return n;
}
if (cache[n] != 0) {
return cache[n];
}
return cache[n] = fib(n - 1, cache) + fib(n - 2, cache);
}Efficient Bottom up approach
public static int fibTabulation(int n) {
int[] cache = new int[n + 1];
cache[0] = 0;
cache[1] = 1;
for (int i = 2; i < cache.length; i++) {
cache[i] = cache[i - 1] + cache[i - 2];
}
return cache[n];
}
Eliminating caching
public static int fibEffec(int n) {
if(n<2){
return n;
}
int first = 0;
int second = 1;
int sum = 0;
for (int i = 2; i < n + 1; i++) {
sum = first + second;
first = second;
second = sum;
}
return sum;
}Complete Program
package com.algo.DP;
public class Demo1 {
public static void main(String[] args) {
int n = 4;
int[] cache = new int[n + 1];
System.out.println(fib(n));
System.out.println(fib(n, cache));
System.out.println(fibTabulation(n));
System.out.println(fibEffec(n));
}
public static int fibEffec(int n) {
if(n<2){
return n;
}
int first = 0;
int second = 1;
int sum = 0;
for (int i = 2; i < n + 1; i++) {
sum = first + second;
first = second;
second = sum;
}
return sum;
}
public static int fibTabulation(int n) {
int[] cache = new int[n + 1];
cache[0] = 0;
cache[1] = 1;
for (int i = 2; i < cache.length; i++) {
cache[i] = cache[i - 1] + cache[i - 2];
}
return cache[n];
}
public static int fib(int n) {
if (n < 2)
return n;
return fib(n - 1) + fib(n - 2);
}
public static int fib(int n, int[] cache) {
if (n < 2) {
return n;
}
if (cache[n] != 0) {
return cache[n];
}
return cache[n] = fib(n - 1, cache) + fib(n - 2, cache);
}
}
Staircase problem
A child is climbing up a the staircase with n steps and hop either 1 step or 2 step at a time.
Implement a method to count how many possible ways the child can climb up the stairs.
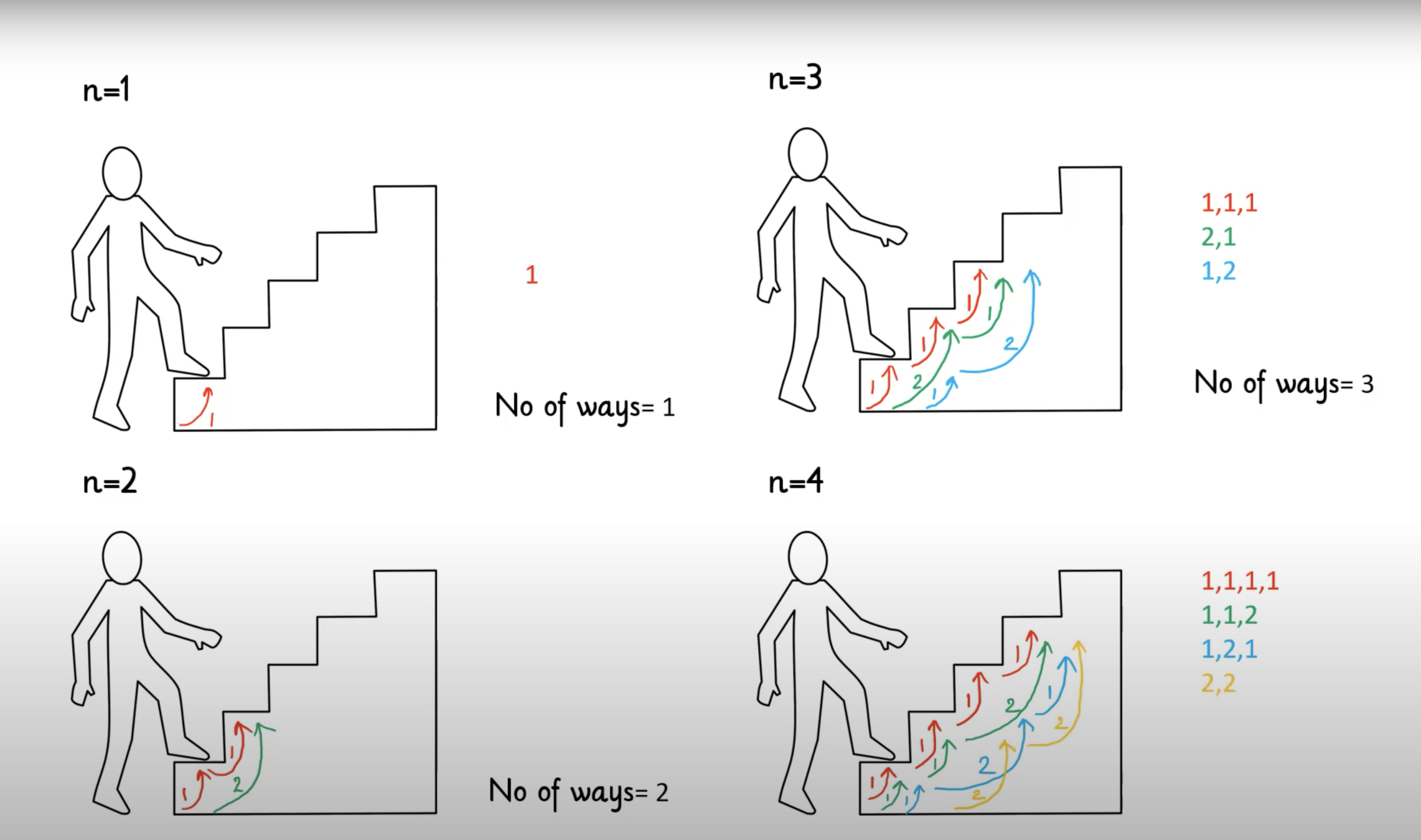
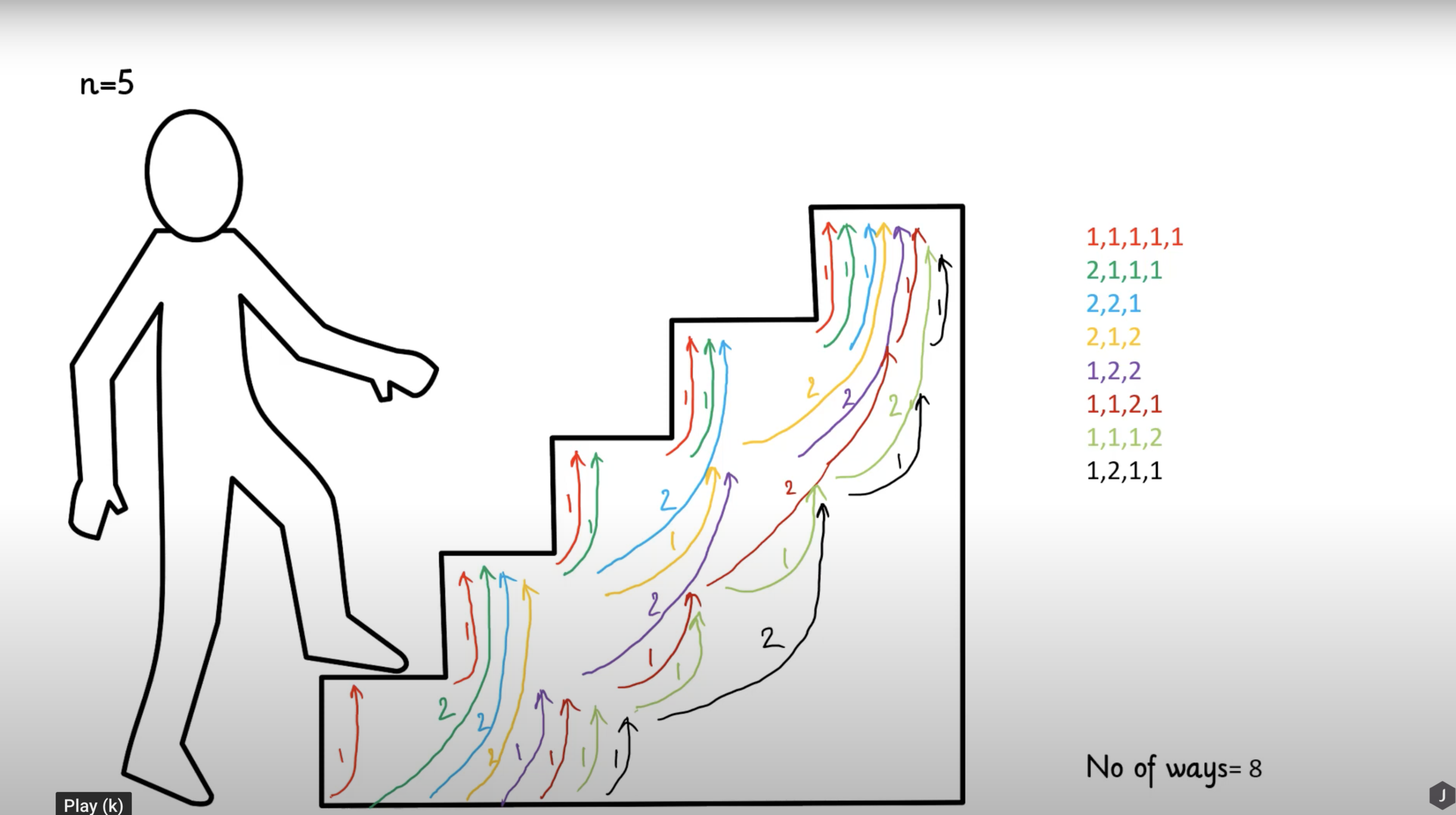
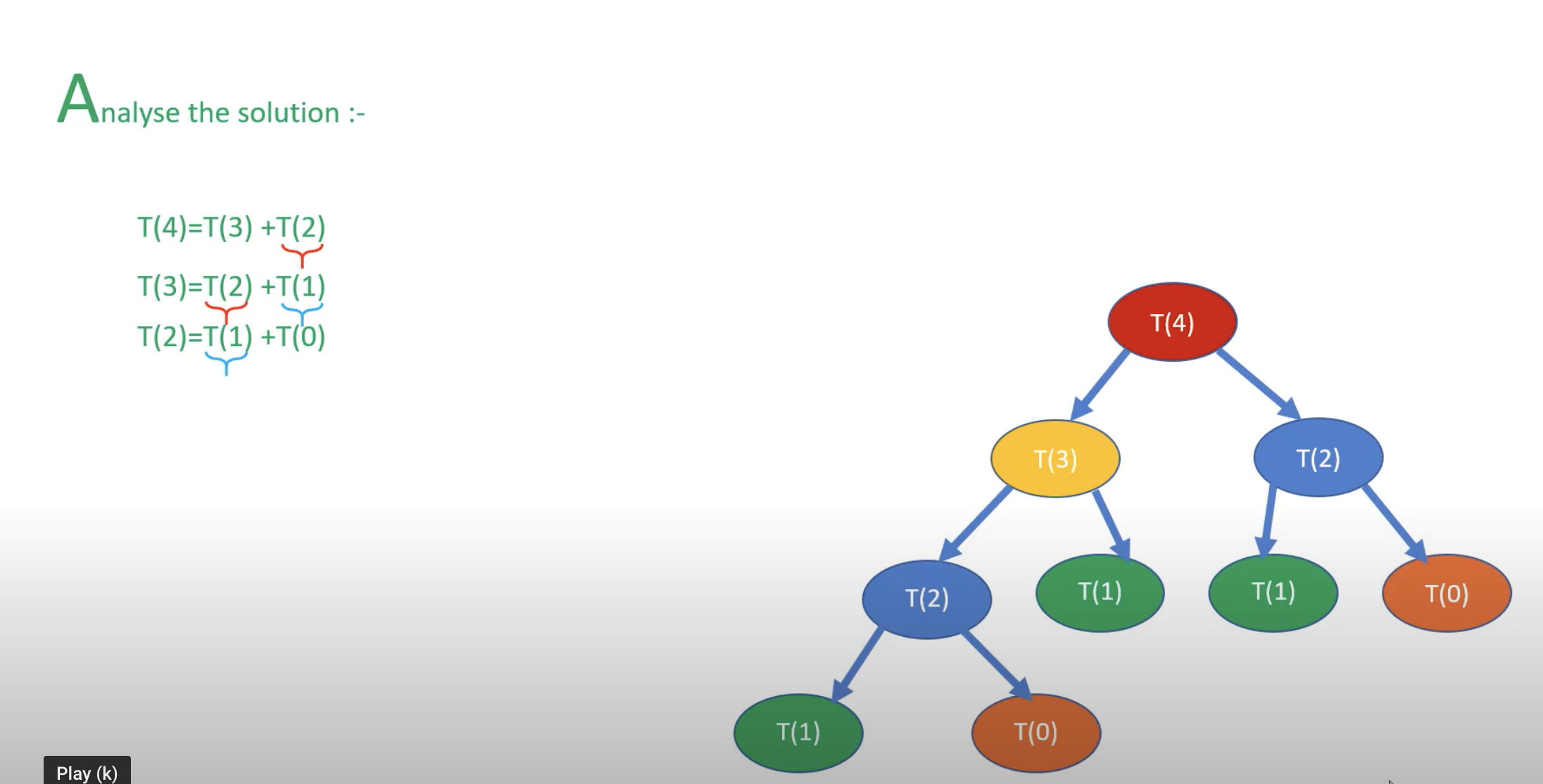
Recursive Solution
static int stairCaseSolution(int n) {
if (n < 0) {
return 0;
}
if (n == 0) {
return 1;
}
return stairCaseSolution(n - 1) + stairCaseSolution(n - 2);
}Recursive Solution with caching (Memoization)
static int stairCaseSolution(int n, int[] arr) {
if (n < 0) {
return 0;
}
if (n == 0) {
return 1;
}
if (arr[n] != 0) {
return arr[n];
}
return arr[n] = stairCaseSolution(n - 1, arr) + stairCaseSolution(n - 2, arr);
}Bottom Up approach (Tabulation )
static int stairCaseBottomUpSolution(int n, int[] arr) {
arr[0] = 1;
arr[1] = 1;
for (int i = 2; i <= n; i++) {
arr[i] = arr[i - 1] + arr[i - 2];
}
return arr[n];
}Tabulation without caching
static int stairCaseBottomUpSolutionWithoutCache(int n) {
int first = 1, second = 1, sum = 0;
for (int i = 2; i <= n; i++) {
sum = first + second;
first = second;
second = sum;
}
return sum;
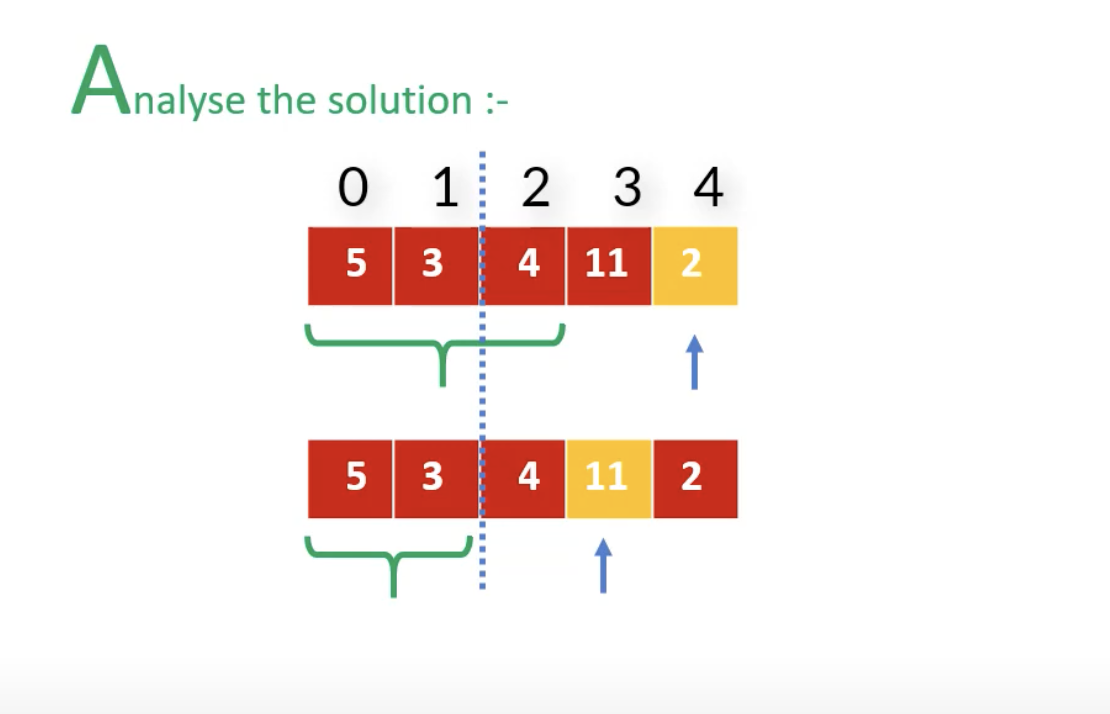
}House Robber problem
- You are a professional robber planning to rob the house along a street.
- Each house has a certain amount of money stashed.
- The only constraint stopping you for robbing each of them is that adjacent houses have security systems connected and it will be automatically contact the police if two adjacent houses were broken into the same night.
- Given a list of non negative integers represent the amount of money you can rob tonight without alerting the police
- Sample 1
- input : {2,7,9,3,1}
- rob house 1,3 and 5
- output : 12
- Sample 2
- input : {5,3,4,11,2}
- rob house : 1 and 4
- output : 16
- Case 1 [ Rob the current house ]:
- if the current ith house is selected for robbery it means (i-1)th and (i+1)th house can't be robbed but can safely proceed to (i-2)th and (i+2)th.
- ith_house _is_selected = current_house_value + rob(i-2)
- Case 2 [ Do not rob the current house]:
- if ith house is not robbed it means robber will get all the possible money of (i-1)th and (i+1)th house and so on.
- ith_house_is_not_selected = rob(i-1)
Recursive Approach
static int robCache(int[] arr, int n, int[] cache) {
if (n < 0) {
return 0;
}
if (cache[n] != 0) {
return cache[n];
}
int ith_house_selected = robCache(arr, n - 2, cache) + arr[n];
int ith_house_not_selected = robCache(arr, n - 1, cache);
return cache[n] = Math.max(ith_house_selected, ith_house_not_selected);
}
static int houseRobberBottomUpSolution(int[] arr, int[] cache) {
cache[0] = arr[0];
cache[1] = Math.max(arr[0], arr[1]);
for (int i = 2; i < arr.length; i++) {
cache[i]=Math.max(cache[i-1],cache[i-2]+arr[i]);
}
return cache[arr.length-1];
}Memoization
Tabulation
static int houseRobberBottomUpSolution(int[] arr, int[] cache) {
cache[0] = arr[0];
cache[1] = Math.max(arr[0], arr[1]);
for (int i = 2; i < arr.length; i++) {
cache[i]=Math.max(cache[i-1],cache[i-2]+arr[i]);
}
return cache[arr.length-1];
}Tabulation without Caching
static int houseRobberBottomUpSolutionWithoutCache(int[] arr) {
int prev2 = arr[0];
int prev1 = Math.max(arr[0], arr[1]);
for (int i = 2; i < arr.length; i++) {
int tmp = prev1;
prev1 = Math.max(prev2 + arr[i], prev1);
prev2 = tmp;
}
return prev1;
}package com.algo.DP;
public class HouseRobberProblem {
public static void main(String[] args) {
int[] arr = {2, 45, 8, 7, 98, 24};
int[] cache = new int[arr.length + 1];
System.out.println(rob(arr, arr.length - 1));
System.out.println(robCache(arr, arr.length - 1, cache));
System.out.println(houseRobberBottomUpSolution(arr,cache));
System.out.println(houseRobberBottomUpSolutionWithoutCache(arr));
}
static int rob(int[] arr, int n) {
if (n < 0) {
return 0;
}
int ith_house_selected = rob(arr, n - 2) + arr[n];
int ith_house_not_selected = rob(arr, n - 1);
return Math.max(ith_house_selected, ith_house_not_selected);
}
static int robCache(int[] arr, int n, int[] cache) {
if (n < 0) {
return 0;
}
if (cache[n] != 0) {
return cache[n];
}
int ith_house_selected = robCache(arr, n - 2, cache) + arr[n];
int ith_house_not_selected = robCache(arr, n - 1, cache);
return cache[n] = Math.max(ith_house_selected, ith_house_not_selected);
}
static int houseRobberBottomUpSolution(int[] arr, int[] cache) {
cache[0] = arr[0];
cache[1] = Math.max(arr[0], arr[1]);
for (int i = 2; i < arr.length; i++) {
cache[i]=Math.max(cache[i-1],cache[i-2]+arr[i]);
}
return cache[arr.length-1];
}
static int houseRobberBottomUpSolutionWithoutCache(int[] arr) {
int prev2 = arr[0];
int prev1 = Math.max(arr[0], arr[1]);
for (int i = 2; i < arr.length; i++) {
int tmp = prev1;
prev1 = Math.max(prev2 + arr[i], prev1);
prev2 = tmp;
}
return prev1;
}
}
Complete Program
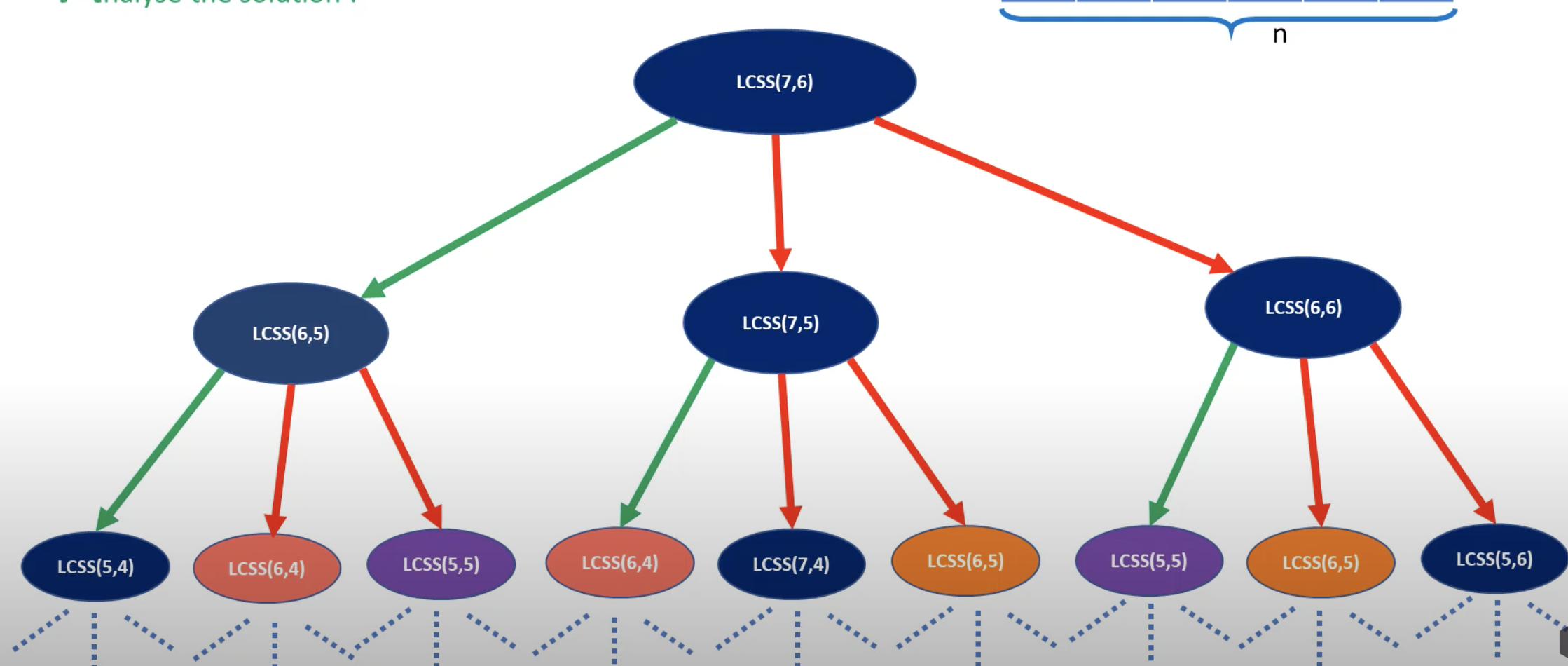
Longest Common substring
- Given two strings S1 and S2, find the length of the longest common substring which is common in both the strings.
- Input :
- S1 : JavaProgrammingLanguage
- S2 : JavaLanguage
- Output : 8
static int longestCommonSubString(char[] str1, char[] str2, int m, int n, int lcsCount) {
if (m <= 0 || n <= 0) {
return lcsCount;
}
int lcsCount1 = lcsCount;
if (str1[m - 1] == str2[n - 1]) {
lcsCount1 = longestCommonSubString(str1, str2, m - 1, n - 1, lcsCount + 1);
}
int lcsCount2 = longestCommonSubString(str1, str2, m, n - 1, 0);
int lcsCount3 = longestCommonSubString(str1, str2, m - 1, n, 0);
return Math.max(lcsCount1, Math.max(lcsCount2, lcsCount3));
}Recursive Solution
Recursive Solution with Caching
static int longestCommonSubStringWithCaching(char[] str1, char[] str2, int m, int n, int lcsCount, int cache[][][]) {
if (m <= 0 || n <= 0) {
return lcsCount;
}
if (cache[m][n][lcsCount] != 0) {
return cache[m][n][lcsCount];
}
int lcsCount1 = lcsCount;
if (str1[m - 1] == str2[n - 1]) {
lcsCount1 = longestCommonSubStringWithCaching(str1, str2, m - 1, n - 1, lcsCount + 1, cache);
}
int lcsCount2 = longestCommonSubStringWithCaching(str1, str2, m, n - 1, 0, cache);
int lcsCount3 = longestCommonSubStringWithCaching(str1, str2, m - 1, n, 0, cache);
return cache[m][n][lcsCount] = Math.max(lcsCount1, Math.max(lcsCount2, lcsCount3));
}
static int longestCommonSubStringBottomUpSolution(char[] str1, char[] str2, int m, int n) {
int result = 0;
int[][] memo = new int[m + 1][n + 1];
for (int i = 0; i <= m; i++) {
for (int j = 0; j <= n; j++) {
if (i == 0 || j == 0) {
memo[i][j] = 0;
} else if (str1[i - 1] == str2[j - 1]) {
memo[i][j] = memo[i - 1][j - 1] + 1;
result = Math.max(memo[i][j], result);
} else {
memo[i][j] = 0;
}
}
}
return result;
}Bottom Up approach
Complete Program
package com.algo.DP;
public class LongestCommonSubStringProblem {
public static void main(String[] args) {
String str = "JavaProgrammingLanguage";
String str2 = "JavaLanguage";
// String str = "JavaProgram";
// String str2 = "JavaProgram";
int m = str.length();
int n = str2.length();
int[][][] cache = new int[m + 1][n + 1][Math.max(m, n) + 1];
System.out.println(longestCommonSubString(str.toCharArray(), str2.toCharArray(), str.length(), str2.length(), 0));
System.out.println(longestCommonSubStringWithCaching(str.toCharArray(), str2.toCharArray(), str.length(), str2.length(), 0, cache));
System.out.println(longestCommonSubStringBottomUpSolution(str.toCharArray(), str2.toCharArray(), str.length(), str2.length()));
}
static int longestCommonSubStringBottomUpSolution(char[] str1, char[] str2, int m, int n) {
int result = 0;
int[][] memo = new int[m + 1][n + 1];
for (int i = 0; i <= m; i++) {
for (int j = 0; j <= n; j++) {
if (i == 0 || j == 0) {
memo[i][j] = 0;
} else if (str1[i - 1] == str2[j - 1]) {
memo[i][j] = memo[i - 1][j - 1] + 1;
result = Math.max(memo[i][j], result);
} else {
memo[i][j] = 0;
}
}
}
return result;
}
static int longestCommonSubStringWithCaching(char[] str1, char[] str2, int m, int n, int lcsCount, int cache[][][]) {
if (m <= 0 || n <= 0) {
return lcsCount;
}
if (cache[m][n][lcsCount] != 0) {
return cache[m][n][lcsCount];
}
int lcsCount1 = lcsCount;
if (str1[m - 1] == str2[n - 1]) {
lcsCount1 = longestCommonSubStringWithCaching(str1, str2, m - 1, n - 1, lcsCount + 1, cache);
}
int lcsCount2 = longestCommonSubStringWithCaching(str1, str2, m, n - 1, 0, cache);
int lcsCount3 = longestCommonSubStringWithCaching(str1, str2, m - 1, n, 0, cache);
return cache[m][n][lcsCount] = Math.max(lcsCount1, Math.max(lcsCount2, lcsCount3));
}
static int longestCommonSubString(char[] str1, char[] str2, int m, int n, int lcsCount) {
if (m <= 0 || n <= 0) {
return lcsCount;
}
int lcsCount1 = lcsCount;
if (str1[m - 1] == str2[n - 1]) {
lcsCount1 = longestCommonSubString(str1, str2, m - 1, n - 1, lcsCount + 1);
}
int lcsCount2 = longestCommonSubString(str1, str2, m, n - 1, 0);
int lcsCount3 = longestCommonSubString(str1, str2, m - 1, n, 0);
return Math.max(lcsCount1, Math.max(lcsCount2, lcsCount3));
}
}
Longest Common Subsequence
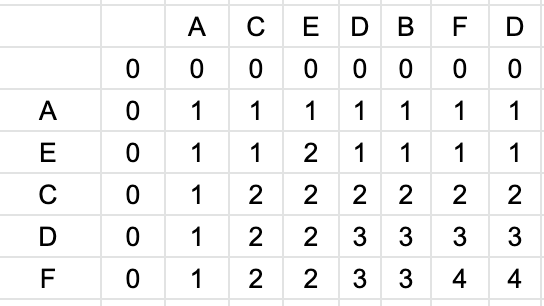
- Given two strings S1 and S2, find the length of the longest common subsequence which is common in both the strings
- Input :
- S1 : ACEDBFD
- S1 : AECDF
- Output : 4
- Explanation : The longest common subsequence is ACDF therefore the length is 4.
Algorithm :
- Case 1 : If character X[i] matches with Y[i], We can recursively match for remaining characters
- Case 2 : If character of both the strings are different, we start two new recursive calls by skipping one character separately from each String.
Recursive Solution
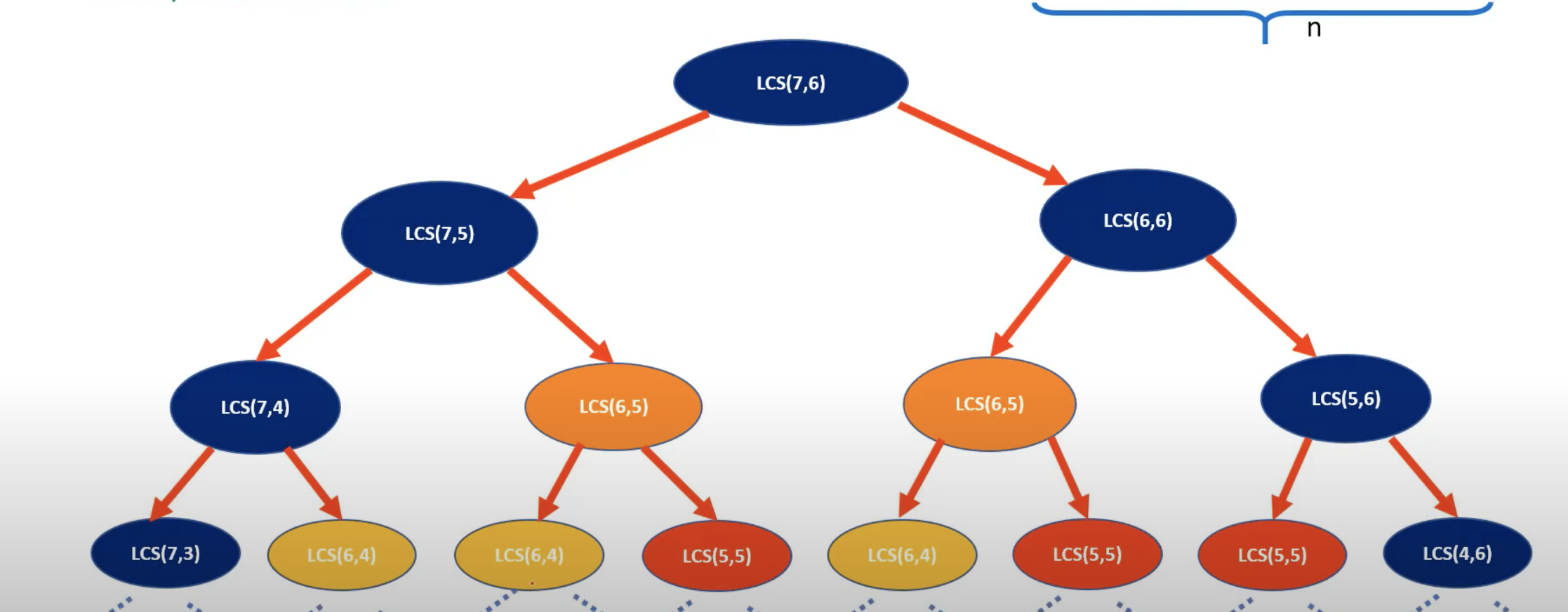
static int longestCommonSubSequenceRecursiveSolution(char[] str1, char[] str2, int m, int n) {
if (m <= 0 || n <= 0) {
return 0;
}
if (str1[m - 1] == str2[n - 1]) {
return 1 + longestCommonSubSequenceRecursiveSolution(str1, str2, m - 1, n - 1);
}
return Math.max(
longestCommonSubSequenceRecursiveSolution(str1, str2, m, n - 1),
longestCommonSubSequenceRecursiveSolution(str1, str2, m - 1, n));
}
Recursive Solution with Caching (Memoization)
static int longestCommonSubSequenceRecursiveSolutionWithCache(char[] str1, char[] str2, int m, int n, int[][] cache) {
if (m <= 0 || n <= 0) {
return 0;
}
if (cache[m][n] != 0) {
return cache[m][n];
}
if (str1[m - 1] == str2[n - 1]) {
return 1 + longestCommonSubSequenceRecursiveSolutionWithCache(str1, str2, m - 1, n - 1, cache);
}
return cache[m][n] = Math.max(
longestCommonSubSequenceRecursiveSolutionWithCache(str1, str2, m, n - 1, cache),
longestCommonSubSequenceRecursiveSolutionWithCache(str1, str2, m - 1, n, cache)
);
}
static int longestCommonSubSequenceBottomUpSolution(char[] str1, char[] str2, int m, int n) {
int[][] memo = new int[m + 1][n + 1];
for (int i = 0; i <= m; i++) {
for (int j = 0; j <= n; j++) {
if (i == 0 || j == 0) {
memo[i][j] = 0;
} else if (str1[i - 1] == str2[j - 1]) {
memo[i][j] = memo[i - 1][j - 1] + 1;
} else {
memo[i][j] = Math.max(memo[i - 1][j], memo[i][j - 1]);
}
}
}
return memo[m][n];
}Tabulation Solution
package com.algo.DP;
public class LongestCommonSubSequenceProblem {
public static void main(String[] args) {
String str = "Javaaid";
String str2 = "Javaid";
int m = str.length();
int n = str2.length();
int[][] cache = new int[m + 1][n + 1];
// System.out.println(longestCommonSubSequenceRecursiveSolution(str.toCharArray(), str2.toCharArray(), m, n));
// System.out.println(longestCommonSubSequenceRecursiveSolutionWithCache(str.toCharArray(), str2.toCharArray(), m, n, cache));
System.out.println(longestCommonSubSequenceBottomUpSolution(str.toCharArray(), str2.toCharArray(), m, n));
}
static int longestCommonSubSequenceBottomUpSolution(char[] str1, char[] str2, int m, int n) {
int[][] memo = new int[m + 1][n + 1];
for (int i = 0; i <= m; i++) {
for (int j = 0; j <= n; j++) {
if (i == 0 || j == 0) {
memo[i][j] = 0;
} else if (str1[i - 1] == str2[j - 1]) {
memo[i][j] = memo[i - 1][j - 1] + 1;
} else {
memo[i][j] = Math.max(memo[i - 1][j], memo[i][j - 1]);
}
}
}
return memo[m][n];
}
static int longestCommonSubSequenceRecursiveSolutionWithCache(char[] str1, char[] str2, int m, int n, int[][] cache) {
if (m <= 0 || n <= 0) {
return 0;
}
if (cache[m][n] != 0) {
return cache[m][n];
}
if (str1[m - 1] == str2[n - 1]) {
return 1 + longestCommonSubSequenceRecursiveSolutionWithCache(str1, str2, m - 1, n - 1, cache);
}
return cache[m][n] = Math.max(
longestCommonSubSequenceRecursiveSolutionWithCache(str1, str2, m, n - 1, cache),
longestCommonSubSequenceRecursiveSolutionWithCache(str1, str2, m - 1, n, cache)
);
}
static int longestCommonSubSequenceRecursiveSolution(char[] str1, char[] str2, int m, int n) {
if (m <= 0 || n <= 0) {
return 0;
}
if (str1[m - 1] == str2[n - 1]) {
return 1 + longestCommonSubSequenceRecursiveSolution(str1, str2, m - 1, n - 1);
}
return Math.max(
longestCommonSubSequenceRecursiveSolution(str1, str2, m, n - 1),
longestCommonSubSequenceRecursiveSolution(str1, str2, m - 1, n));
}
}
Complete Program
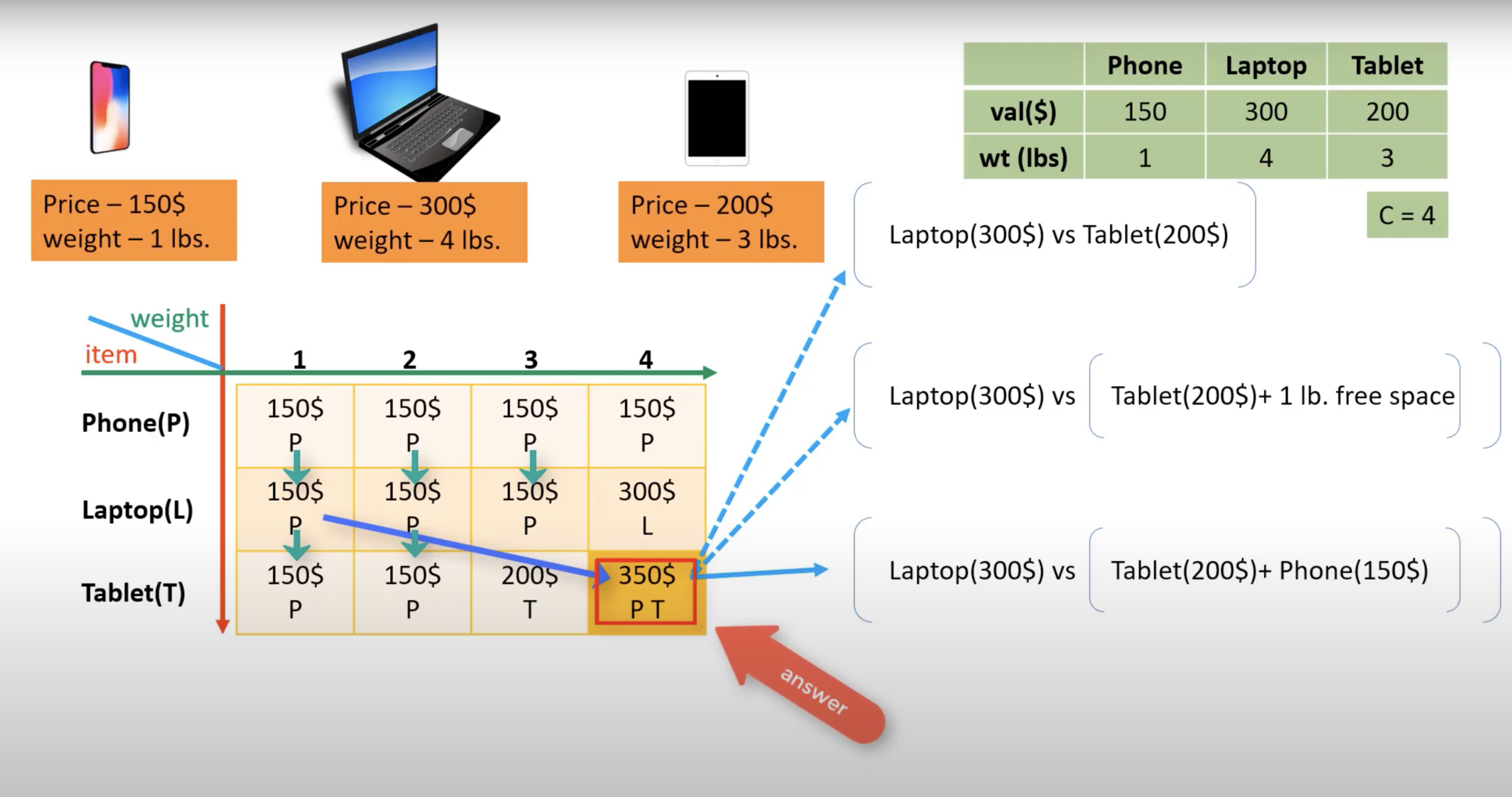
0-1 Knapsack Problem
- Given a Set S of n items each with its own value V and Weight W for all 1<=i<=n and maximum knapsack capacity C, compute the maximum value of the items that you can carry. You cannot take fractions of items.
- Sample
- val {150, 300, 200}
- wt {1,4,3}
package com.algo.DP;
public class ZeroOneKnapsackProblem {
public static void main(String[] args) {
int[] value = {150, 300, 200};
int[] weight = {1, 4, 3};
int capacity = 4;
System.out.println(zeroOneKnapsackProblem(value,weight,capacity));
}
public static int zeroOneKnapsackProblem(int[] value, int[] weight, int capacity) {
int n = value.length;
int[][] memo = new int[n + 1][capacity + 1];
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= capacity; j++) {
if (i == 0 || j == 0) {
memo[i][j] = 0;
} else if (weight[i - 1] > j) {
memo[i][j] = memo[i - 1][j];
}else{
memo[i][j]=Math.max(value[i-1]+memo[i-1][j-weight[i-1]],memo[i-1][j]);
}
}
}
return memo[n][capacity];
}
}
Dynamic Programming for Java Developers Part 2
Write an efficient program to find the sum of contiguous subarray within a one-dimensional array of numbers that has the largest sum.

| 4 | 3 | -2 | 6 | 7 | -10 | -10 | 4 | 5 | 9 |
|---|
- 4 -> 4
- 7 -> 4,3
- 5 -> 4,3,-2
- 11-> 4,3,-2,6
- 18 -> 4,3,-2,6,7
- 8 -> 4,3,-2,6,7,-10
- -2 -> 4,3,-2,6,7,-10,-10
- 4 -> 4
- 9 -> 4,5
- 18 -> 4,5,9
- 15-> 4,5,9,-3
- 19-> 4,5,9,-3,4
- 26-> 4,5,9,-3,4,7
- 35->4,5,9,-3,4,7,9
- 4 -> 4
- 7 -> 4,3
- 5 -> 4,3,-2
- 11-> 4,3,-2,6
- 18 -> 4,3,-2,6,7
- 19-> 4,5,9,-3,4
- 26-> 4,5,9,-3,4,7
- 35->4,5,9,-3,4,7,9
| -3 | 4 | 7 | 9 |
|---|
Kadane's Theorm
Current Best
Overall Best
package com.algo.DP;
public class KadaneAlgorithm {
public static void main(String[] args) {
int[] arr = {4, 3, -2, 6, -12, 7, -1, 6};
System.out.println(maxNumberInArray(arr));
}
public static int maxNumberInArray(int[] arr) {
int currentMax = arr[0];
int maxSoFar = arr[0];
for (int i = 1; i < arr.length; i++) {
currentMax = currentMax + arr[i];
if (currentMax < arr[i]) {
currentMax = arr[i];
}
if (maxSoFar < currentMax) {
maxSoFar = currentMax;
}
}
return maxSoFar;
}
}
The Longest Increasing Subsequence (LIS) problem is to find the length of the longest subsequence of a given sequence such that all elements of the subsequence are sorted in increasing order. For example, the length of LIS for {10, 22, 9, 33, 21, 50, 41, 60, 80} is 6 and LIS is {10, 22, 33, 50, 60, 80}.
Longest Increasing Subsequence
| 10 | 22 | 9 | 33 | 21 | 50 | 41 | 60 | 80 | 1 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 1 | 3 | 2 | 4 | 4 | 5 | 6 | 1 |
| - | - | - | - | - | - | - | - | - | - |
| 10 | 10 | 9 | 10 | 10 | 10 | 10 | 10 | 10 | 3 |
| 22 | 22 | 21 | 22 | 22 | 22 | 22 | |||
| 33 | 33 | 33 | 33 | 33 | |||||
| 50 | 41 | 50 | 50 | ||||||
| 60 | 60 | ||||||||
| 80 |
Elements
Count
package com.algo.DP;
import java.util.Arrays;
public class LongestIncreasingSequence {
public static void main(String[] args) {
int[] arr = {10,22,9,33,21,50,41,60,80,1};
System.out.println(findLIS(arr));
}
public static int findLIS(int[] arr) {
int[] dp = new int[arr.length];
dp[0] = 1;
int maxo = 0;
for (int i = 1; i < arr.length; i++) {
int max = 0;
for (int j = 0; j < i; j++) {
if (arr[i] > arr[j] && dp[j] > max) {
max = dp[j];
}
dp[i] = max + 1;
}
if (dp[i] > maxo) {
maxo = dp[i];
}
System.out.println(Arrays.toString(dp));
}
return maxo;
}
}
Given a set of non-negative integers, and a value sum, determine if there is a subset of the given set with sum equal to given sum.
example
Input: set[] = {3, 34, 4, 12, 5, 2}, sum = 9
Output: True
There is a subset (4, 5) with sum 9.
Input: set[] = {3, 34, 4, 12, 5, 2}, sum = 30
Output: False
There is no subset that add up to 30.
Target Sum Subset
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|
| F | F | F | F | F | F | F | F | F | F |
| F | F | F | T | F | F | F | F | F | F |
| F | T | F | T | F | T | F | F | F | F |
| F | T | F | T | F | T | T | F | T | F |
| T | T | T | T | T | T | T | T | T | T |
| T | T | T | T | T | T | T | T | T | T |
| 0 | |
|---|---|
| X | T |
| 4 | T |
| 2 | T |
| 7 | T |
| 1 | T |
| 3 | T |
Input :
Array = {4,5,7,1,3}
Sum=10
package com.algo.DP;
public class TargetSubSets {
public static void main(String[] args) {
int[] arr = {4, 2, 7, 1, 3};
int target = 59;
System.out.println(targetSubset(arr, target));
}
public static boolean targetSubset(int[] arr, int target) {
boolean[][] dp = new boolean[arr.length + 1][target + 1];
for (int i = 0; i < dp.length; i++) {
for (int j = 0; j < dp[i].length; j++) {
if (i == 0 && j == 0) {
dp[i][j] = true;
} else if (i == 0) {
dp[i][j] = false;
} else if (j == 0) {
dp[i][j] = true;
} else {
if (dp[i - 1][j] == true) {
dp[i][j] = true;
} else {
int val = arr[i - 1];
if (val <= j) {
if(dp[i-1][j-val]==true){
dp[i][j]=true;
}
}
}
}
}
}
return dp[arr.length][target];
}
}
Given a gold mine of n*m dimensions. Each field in this mine contains a positive integer which is the amount of gold in tons. Initially the miner is at first column but can be at any row. He can move only (right->,right up /,right down\) that is from a given cell, the miner can move to the cell diagonally up towards the right or right or diagonally down towards the right. Find out maximum amount of gold he can collect.
Gold Mine Problem
| - | - | - | - | - | - |
|---|---|---|---|---|---|
| 0 | 1 | 4 | 2 | 8 | 2 |
| 4 | 3 | 6 | 5 | 0 | 4 |
| 1 | 2 | 4 | 1 | 4 | 6 |
| 2 | 0 | 7 | 3 | 2 | 2 |
| 3 | 1 | 5 | 9 | 2 | 4 |
| 2 | 7 | 0 | 8 | 5 | 1 |
| - | - | - | - | - | - |
|---|---|---|---|---|---|
| 26 | 24 | 21 | 14 | 12 | 2 |
| 31 | 26 | 23 | 17 | 6 | 4 |
| 28 | 27 | 21 | 11 | 10 | 6 |
| 29 | 25 | 25 | 13 | 8 | 2 |
| 33 | 26 | 23 | 18 | 6 | 4 |
| 32 | 30 | 18 | 17 | 9 | 1 |
package com.algo.DP;
public class GoldMine {
public static void main(String[] args) {
int[][] arr = {
{0, 1, 4, 2, 8, 2},
{4, 3, 6, 5, 0, 4},
{1, 2, 4, 1, 4, 6},
{2, 0, 7, 3, 2, 2},
{3, 1, 5, 9, 2, 4},
{2, 7, 0, 8, 5, 1}
};
System.out.println(goldMine(arr));
}
public static int goldMine(int[][] arr) {
int[][] dp = new int[arr.length][arr.length];
for (int j = arr.length - 1; j >= 0; j--) {
for (int i = arr.length - 1; i >= 0; i--) {
if (j == arr.length - 1) {
dp[i][j] = arr[i][j];
} else if (i == 0) {
dp[i][j] = arr[i][j] + Math.max(dp[i + 1][j + 1], dp[i][j + 1]);
} else if (i == arr.length - 1) {
dp[i][j] = arr[i][j] + Math.max(dp[i - 1][j + 1], dp[i][j + 1]);
} else {
dp[i][j] = arr[i][j] + Math.max(dp[i][j + 1], Math.max(dp[i - 1][j + 1], dp[i + 1][j + 1]));
}
}
}
int max = dp[0][0];
for (int i = 1; i < dp.length; i++) {
if (dp[i][0] > max) {
max = dp[i][0];
}
}
return max;
}
}
The cost of a stock on each day is given in an array, find the max profit that you can make by buying and selling in those days. For example, if the given array is {100, 180, 260, 310, 40, 535, 695}, the maximum profit can earn by buying on day 0, selling on day 3. Again, buy on day 4 and sell on day 6. If the given array of prices is sorted in decreasing order, then profit cannot be earned at all.
Stock Buy and Sell Problem
6
5
4
3
2
1
0
7
| 1 | 2 | 1 | 2 | 3 | 2 | 3 | 4 | 3 | 4 |
|---|
| 5 |
|---|
1
2
8
7
6
5
4
3
10
9
package com.algo.DP;
public class StockBuyAndSell {
public static void main(String[] args) {
int arr[] = {1, 2, 1, 2, 3, 2, 3, 4, 3, 4, 5};
System.out.println(stockBuyAndSell(arr));
}
public static int stockBuyAndSell(int arr[]) {
int bd = 0;
int sd = 0;
int profit = 0;
for (int i = 1; i < arr.length; i++) {
if (arr[i] >= arr[i - 1]) {
sd++;
} else {
profit += arr[sd] - arr[bd];
bd = sd = i;
}
}
profit += arr[sd] - arr[bd];
return profit;
}
}
Given a “2 x n” board and tiles of size “2 x 1”, count the number of ways to tile the given board using the 2 x 1 tiles. A tile can either be placed horizontally i.e., as a 1 x 2 tile or vertically i.e., as 2 x 1 tile.
Tiling Problem
2 x 1
2 x 2
2 x 3
2 x 4
2 x 5
| Size | Ways |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 5 |
| 5 | 8 |
package com.algo.DP;
public class TilingDominoes {
public static void main(String[] args) {
int n = 3;
System.out.println(tilingDominoes(n));
}
public static int tilingDominoes(int n) {
if(n<=2){
return n;
}
int first = 1;
int second = 2;
int ways = 0;
for (int i = 3; i <= n; i++) {
ways = first + second;
first = second;
second = ways;
}
return ways;
}
}
Given a rod of length n inches and an array of prices that includes prices of all pieces of size smaller than n. Determine the maximum value obtainable by cutting up the rod and selling the pieces. For example, if the length of the rod is 8 and the values of different pieces are given as the following, then the maximum obtainable value is 22 (by cutting in two pieces of lengths 2 and 6)
length | 1 2 3 4 5 6 7 8 -------------------------------------------- price | 1 5 8 9 10 17 17 20
Rod Cutting Problem
| Cost | N | 1 | 5 | 8 | 9 | 10 | 17 | 17 | 20 |
|---|---|---|---|---|---|---|---|---|---|
| Wood Length | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Best Cost | 0 | 1 | 5 | 8 | 10 | 13 | 17 | 18 | 22 |
| Combination (Best) | 0 | 1- 0 | 2-0 | 3-0 | 2-2 | 2-3 | 6-0 | 6-1 | 2-6 |
package com.algo.DP;
import java.util.Arrays;
public class RodCutting {
public static void main(String[] args) {
int[] prices = {1, 5, 8, 9, 10};
System.out.println(rodCutting(prices));
}
public static int rodCutting(int[] prices) {
int[] np = new int[prices.length + 1];
for (int i = 0; i < prices.length; i++) {
np[i + 1] = prices[i];
}
int[] dp = new int[np.length];
dp[0] = 0;
dp[1] = np[1];
for (int i = 2; i < dp.length; i++) {
dp[i] = np[i];
int li = 1;
int ri = i - 1;
while (li <= ri) {
if (dp[i] < dp[li] + dp[ri]) {
dp[i] = dp[li] + dp[ri];
}
li++;
ri--;
}
}
System.out.println(Arrays.toString(dp));
return dp[dp.length - 1];
}
}
The following is a description of the instance of this famous puzzle involving n=2 eggs and a building with k=36 floors.
Suppose that we wish to know which stories in a 36-story building are safe to drop eggs from, and which will cause the eggs to break on landing. We make a few assumptions:
…..An egg that survives a fall can be used again.
…..A broken egg must be discarded.
…..The effect of a fall is the same for all eggs.
…..If an egg breaks when dropped, then it would break if dropped from a higher floor.
…..If an egg survives a fall then it would survive a shorter fall.
…..It is not ruled out that the first-floor windows break eggs, nor is it ruled out that the 36th-floor do not cause an egg to break.
If only one egg is available and we wish to be sure of obtaining the right result, the experiment can be carried out in only one way. Drop the egg from the first-floor window; if it survives, drop it from the second-floor window. Continue upward until it breaks. In the worst case, this method may require 36 droppings. Suppose 2 eggs are available. What is the least number of egg-droppings that is guaranteed to work in all cases?
7 f
3 e
Here we need to find the minimum attempts in which we will find the critical floor. Critical floor (i.e from where egg will break).
Base cases
f=0 -> 0
f=1-> 1
e=0 -> X
e=1 -> f
Egg Dropping Problem
e|f
Survived
Broke
e|f-k
e-1|k-1
kth Floor
7 floors 3 eggs
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|
| 0 | - | - | - | - | - | - | - | - |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 0 | 1 | 2 | 2 | 3 | 3 | 3 | 4 |
| 3 | 0 | 1 | 2 | 2 | 3 | 3 | 3 | 3 |
Floors
Eggs
3,3,3,2,3,3,3
2 E/ 2F
1 F
2 F
Broke
Survive
Broke
Survive
1E/ 0F = 0
2 E/ 1F = 1
1 E/ 1F = 1
2 E/ 0F = 0
Max(1,0)=1
Max(0,1)=1
Min(1,1)+1=2
2E|3F
2E|0F =0
1E|2F=2
2E|1F =1
1E|1F =1
2E|2F=2
1E|0F=0
1F
2F
3F
Broke
Survive
Broke
Survive
Broke
Survive
Max(2,0)=2
Max(1,1)=1
Max(0,2)=2
Min(2,1,2)+1=2
package com.algo.DP;
public class EggDropping {
public static void main(String[] args) {
int floors = 7;
int eggs = 3;
System.out.println(eggDropping(eggs, floors));;
}
public static int eggDropping(int n, int k) {
int[][] dp = new int[n + 1][k + 1];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= k; j++) {
if (i == 1) {
dp[i][j] = j;
} else if (j == 1) {
dp[i][j] = 1;
} else {
int min = Integer.MAX_VALUE;
for (int mj = j - 1, pj = 0; mj >= 0; mj--, pj++) {
int v1 = dp[i][mj];// egg survive
int v2 = dp[i - 1][pj];// egg breaks
int val = Math.max(v1, v2);
min = Math.min(val, min);
}
dp[i][j] = min + 1;
}
}
}
return dp[n][k];
}
}

Java 9
By Pulkit Pushkarna
Java 9
- 1,221



