L-systems as Rose Trees

Wiebe-Marten Wijnja
Summary
- L-systems?
- Existing Algorithms
- Rose Trees?
- New Algorithms
- Benchmarking
- Conclusions
What is an L-system?
- What: Parallel Rewrite System
- Why: Plants, Trees, Cells, Fractals
- How:
-
generation
- (short) procedural description \(\longrightarrow\) (long) string
-
interpretation
- (long) string \(\longrightarrow\) 2D/3D picture/statistic/...
-
generation


L-system Generation
Theory
alphabet: A set of symbols \(V\)
axiom: starting string \(\omega \in V^+\)
production rules: \(P \subset V \times V^+\)
Each rule is usually written as \( a \rightarrow \chi \) where:
- \(a\), is called the antecedent
- \(\chi\), is called the consequent
Context-free L-system \(G = \langle V, \omega, P \rangle\)
Deterministic Context-Free ('D0')
more powerful classes of L-systems expand on this
L-system Generation
Theory
alphabet: A set of symbols \(V\)
axiom: starting string \(\omega \in V^+\)
production rules: \(P \subset V \times V^+\)
Each rule is usually written as \( a \rightarrow \chi \) where:
- \(a\), is called the antecedent
- \(\chi\), is called the consequent
Context-free L-system \(G = \langle V, \omega, P \rangle\)
Generation: transforming $$ \mu = a_1 a_2\ldots a_n $$ into
$$ \nu = \chi_1 \chi_2 \ldots \chi_n $$
... and repeat as desired
to arbitrary depth \(d\)
Deterministic Context-Free ('D0')
more powerful classes of L-systems expand on this
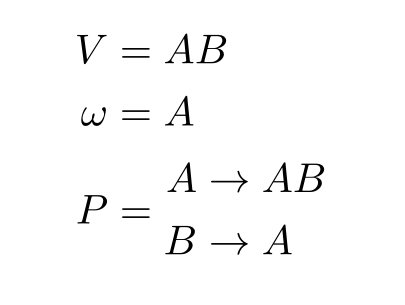

0
1
2
3
L-system Generation
Example: Algae
L-system Generation
Example: Plant
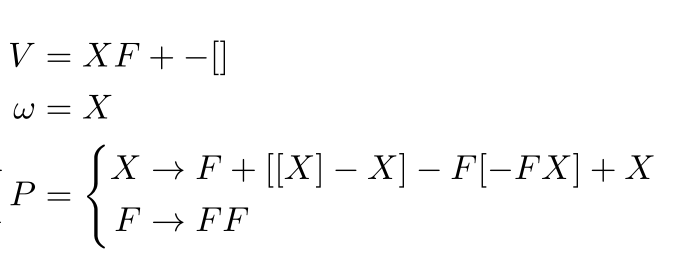

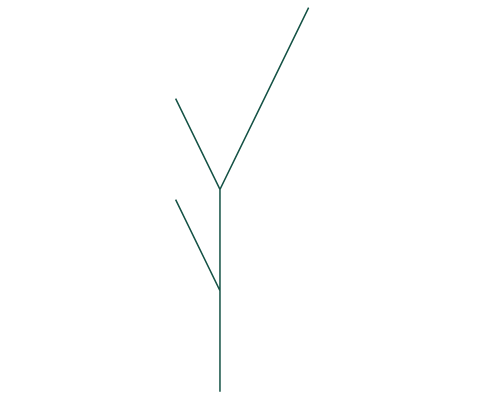






L-system Generation
Algorithm
rewriteString(rules: LSystemRules, string: String) {
string
|> map(|symbol| lookupSymbol(rules, symbol))
|> flatten()
}sequentialRewrite(rules: LSystemRules, string: String, depth: ℤ) {
if depth == 0 {
string
} else {
let result <- rewriteString(string, rules);
sequentialRewrite(rules, result, depth - 1)
}
}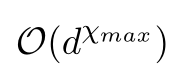
L-system Generation
Algorithm
rewriteString(rules: LSystemRules, string: String) {
string
|> map(|symbol| lookupSymbol(rules, symbol))
|> flatten()
}sequentialRewrite(rules: LSystemRules, string: String, depth: ℤ) {
if depth == 0 {
string
} else {
let result <- rewriteString(string, rules);
sequentialRewrite(rules, result, depth - 1)
}
}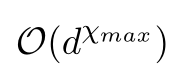
Oof \(\longrightarrow\)
L-system Generation
Problems
- Paralellize?
- Prevent repeated work?
L-system Generation
Problems
- Paralellize? \(\rightarrow\) Gathering results = difficult
- Prevent repeated work?
L-system Generation
Lipp-Wonka-Wimmer
lippWonkaWimmerRewrite(rules: LSystemRules, string: String, depth: ℤ)
if depth == 0 {
string
} else {
let rewrite_lengths <- scatterJoin(string, |string_part|
rewriteLength(string_part, rules)
);
let mut result <- allocateString(∑(rewrite_lengths));
let indexes <- prefixSum(rewrite_lengths);
scatterJoin(⧼string, indexes, rewrite_lengths⧽, |⧼string_part, start_index, length⧽|
let end_index <- start_index + length;
result[start_index..end_index] <- rewriteString(string_part, rules);
);
lippWonkaWimmerRewrite(rules, result, depth - 1)
}- 3 boundaries
- threads need to wait for slowest
- still repeated work
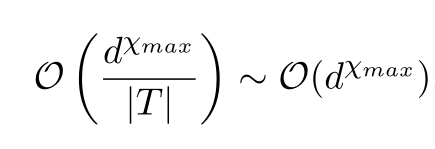
Can we do better?
Rose Trees
- 'multi-way' tree
- Each node has many (ordered) children
Rose Trees
- 'multi-way' tree
- Each node has many (ordered) children
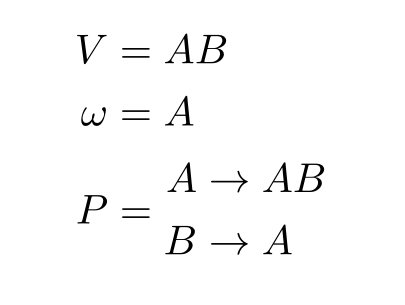

Rose Trees
- 'multi-way' tree
- Each node has many (ordered) children
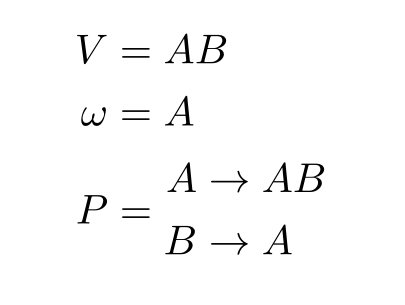

\(\uparrow\) Always the same!
Rose Trees
- Different L-system generation algorithms ⟶ different tree traversals
- Rules are self-similar at every level ⟶ prevent repeated work!
Still holds true for more powerful classes of L-systems,
with some exceptions

TreeConquer
- Depth-first tree-traversal
- 'Parallel Divide-And-Conquer'

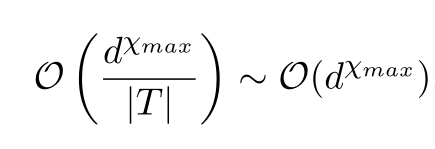
treeConquerRewrite(rules: LSystemRules, string: String, depth: ℤ){
if(depth == 0) {
string
} else if(*small amount of work*) {
let result <- rewriteString(string, rules);
treeConquerRewrite(rules, result, depth - 1);
} else { /* string is long, large amount of work */
let (left_half, right_half) <- splitInHalf(string);
let (left_res, right_res) <- forkJoin(
|| treeConquerRewrite(rules, left_half, depth),
|| treeConquerRewrite(rules, right_half, depth)
);
concatenate(left_res, right_res)
}
}Penultimate
- Leverage structure of rules
- same at every level
- flatten, bottom-up

penultimateRewrite(rules: LSystemRules, string: String, depth: ℤ) {
if depth == 0 {
string
} else {
let mut flat_rules <- rules;
for depth > 1; depth <- depth - 1 {
flat_rules <- flattenRules(rules, flat_rules);
}
rewriteString(string, flat_rules)
}
}
Variant: PenultimateSquaring, based on exponentiation by squaring,
needs only \(\mathcal{O}(\log(d))\) rewrites.
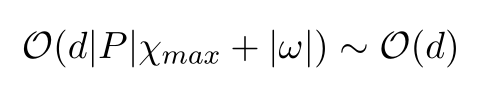
Benchmarking is fun!
Benchmarking is fun!

Benchmarks
- Without Peregrine, it would have taken weeks rather than days...
- ...if finishing at all: 16+ GB of RAM usage for some L-systems at double-digit depths
- Thank you, Peregrine!
But now, time for graphs!
Algae
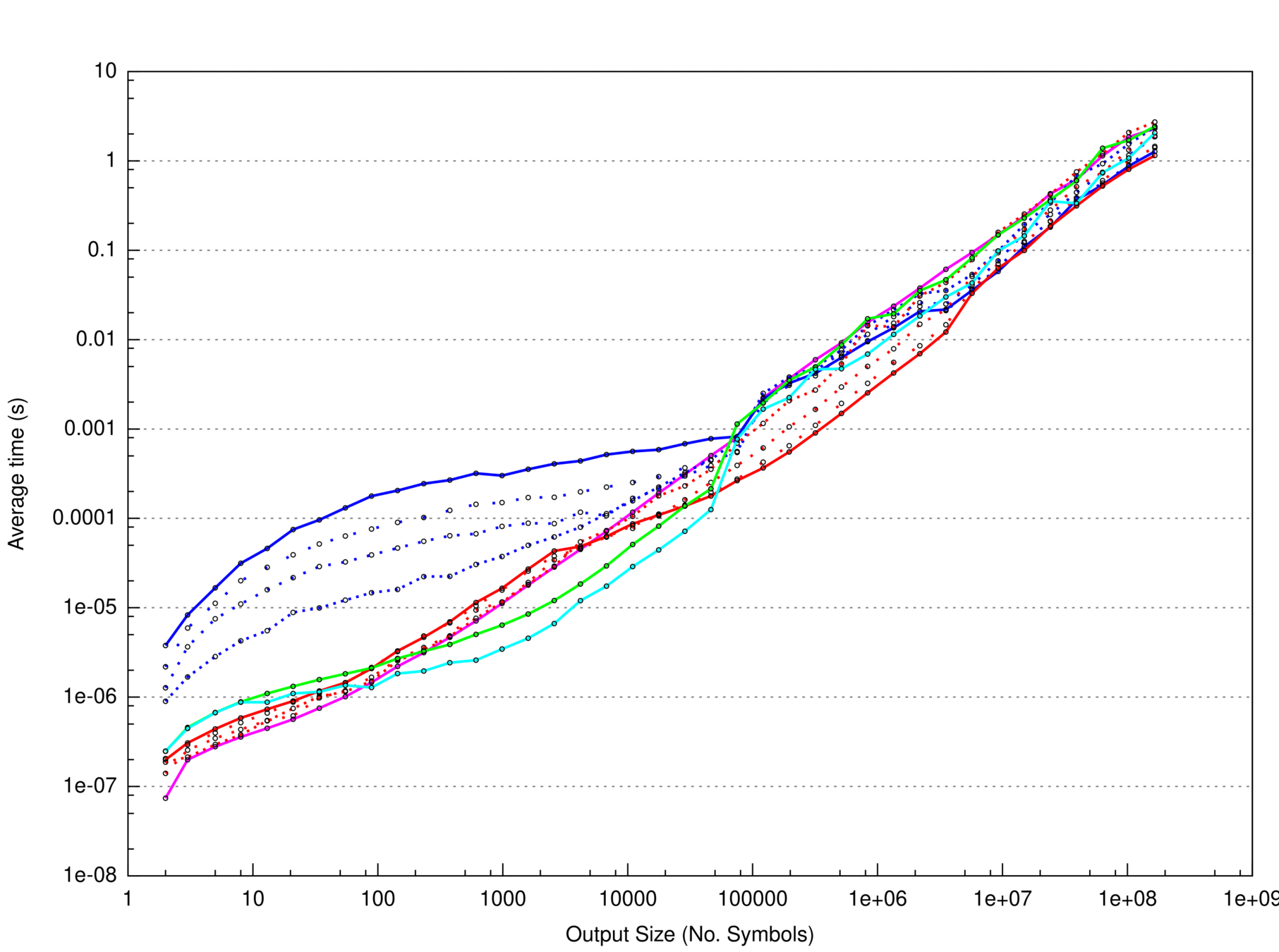
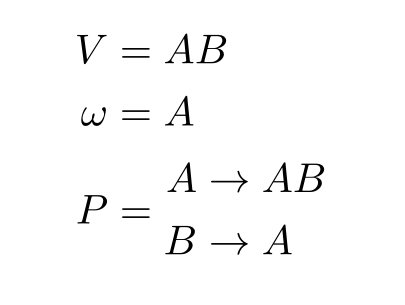

Koch

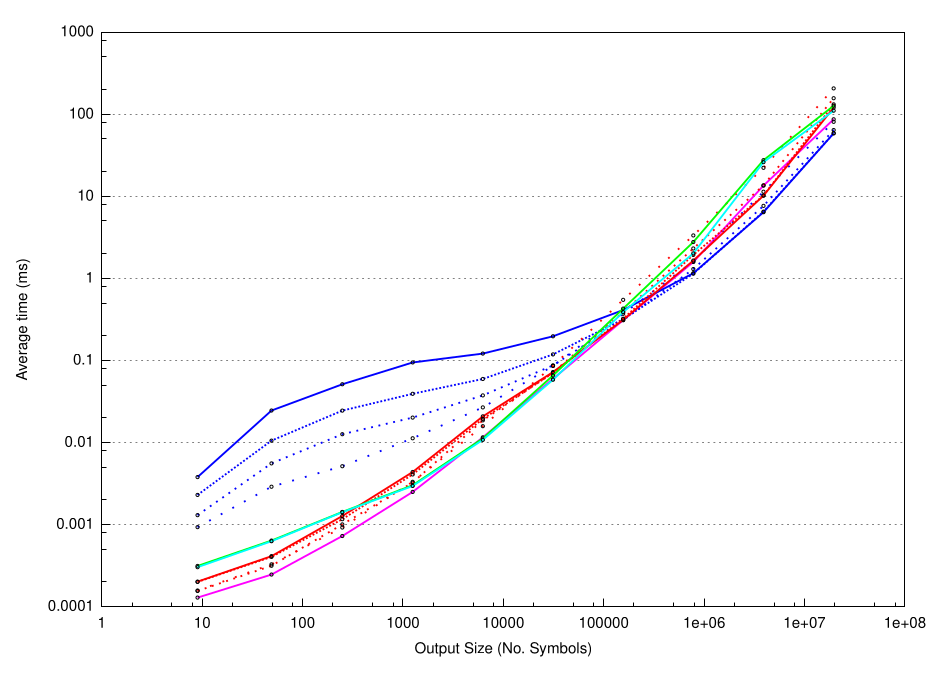
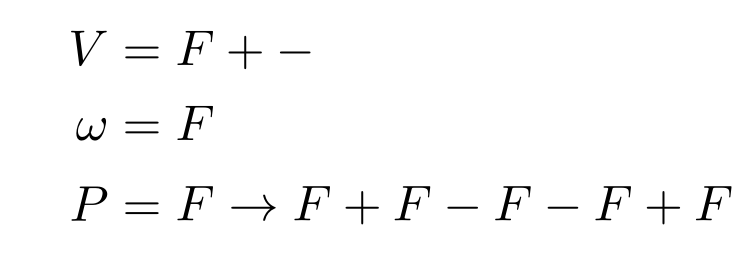

Plant
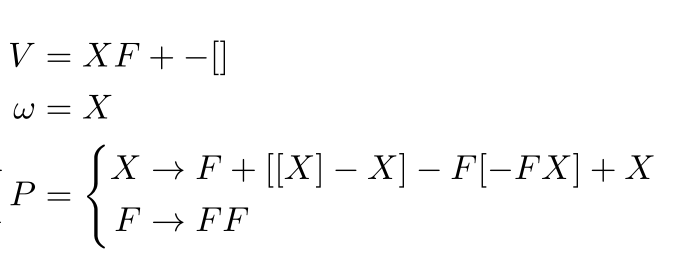



AlphabetExplosion



More graphs in the report
Conclusions

Remarks
- How fast it 'fast enough'?
- generation does not seem to be the bottleneck
- At double-digit depths, gigabytes of RAM are used
Summary
- L-systems?
- Existing Algorithms
- Rose Trees?
- New Algorithms
- Benchmarking
- Conclusions
Thank you!
Thanks to
- Job Talle for his web-applet to quickly render arbitrary L-systems
- Luc van den Brand for making me interested in L-systems in the first place
-
Jiří Kosinka for always being available to answer my weird questions
Thank you!
Questions?
L-systems as Rose Trees
By qqwy
L-systems as Rose Trees
- 1,447



