Centro de Investigación y Docencia Económicas, A. C.
Maestría en economía
Economía Pública
Externalidades
Rafael Martínez Martínez
Agosto-Diciembre 2020
Se presentan notas de estudio del tema de externalidades. Se sigue al libro de Laffont
Laffont, J.J, (1998). Fundamentals of Public Economics. THE MIT PRESS
Fallas de mercado.
Introducción conceptual a tópicos de Economía Pública
Contenido
1. Externalidades
1.1 La Naturaleza de las Externalidades
1.2 Asignación Óptima de Recursos
1.3 Equilibrio Competitivo de Propiedad Privada
1.4 Tipos de Intervención Pública
1.5 Conclusiones
1.6 La compatibilidad de los Retornos Crecientes y la Competencia Perfecta
1.7 Externalidades y Teoría de Juegos
1.8 Una Rehabilitación de las Externalidades Pecuniarias
1.1 La Naturaleza de las Externalidades
- Introducción
- Notación
- Definición de Externalidad
- Ejemplos
Introducción
Nos vemos afectados por el consumo de terceros:
- vecinos que hacen ruido y estás preparando el tema de externalidades (utilidad)
- gente que no fuma en casa y estás de invitado (consumo)
- vecino que contrata internet de banda ancha y eres webmaster (producción)
De igual forma por la producción:
- apple aumenta su producción de tablets y vendes fundas (producción)
- Contaminación de empresas no te permite realizar actividades al aire libre (consumo)
- El vecino es sonidero y sigues preparando el tema de externalidades (utilidad)
El salmón y el aguacate, los alimentos de moda.
El consumo de estos alimentos produce efectos en agentes económicos en regiones de Chile (salmón) y México (aguacate),
Notación
\(X^i \subset \mathbb{R}_+^L\) conjunto de consumo para le consumidor \(i\)
\(L\) número de bienes, \(l=1,\ldots,L\)
\(I\) número de consumidores, \(i=1,\ldots,I\)
\(J\) número de firmas, \(j=1,\dots,J\)
\(x^i=(x_1^i,\ldots,x_L^i )\in X^i\), vector de consumo
\(w^i=(w_1^i,\ldots,w_L^i )\in \mathbb{R}_+^L\), vector de dotación
\(Y^j \subset \mathbb{R}^L\) conjunto de producción para la firma \(j\)
\(y^j=(y_j^i,\ldots,y_L^j )\in Y^j\), vector de producción
\(f^j\), función de producción
\(p \in \mathbb{R}_+^L\), vector de precios
\(p\cdot y^j\), beneficios de la empresa \(j\)
\(\theta^{ij}\in\mathbb{R}_+\), contribución de la firma \(j\) al consumidor \(i\)
\(R^{i}=p\cdot w^i+\sum\limits_j\theta^{ij}p\cdot y^j\), ingreso del consumidor \(i\)
Externalidad
Cualquier efecto indirecto que la actividad de producción o consumo tenga sobre la función de utilidad, el conjunto de consumo o el conjunto de producción.
Definición de Externalidad
Efecto indirecto. El efecto es creado por un agente económico distinto al afectado (efecto externo) y tal efecto no se transmite mediante los precios (no pecuniario).
Nota: efectos externos no pecuniarios conocidos como efectos externos tecnológicos
- Externalidad por consumo
- Externalidad por producción
X^{'i}\\
Y^{'j}\\
U^{'i}
X^i\\
Y^j\\
U^i\\
Ejemplo 1
Se tiene dos bienes,
- vitaminas \(\equiv x_1^i\)
- nadar \(\equiv x_2^i\)
La producción contamina el rio,
- contaminación \(\equiv y\)
X^{'i}=X^{i}\left(y^{1}, \ldots, y^{J}, x^{1}, \ldots, x^{i-1}, x^{i+1}, \ldots, x^{I}\right)
X^{i}
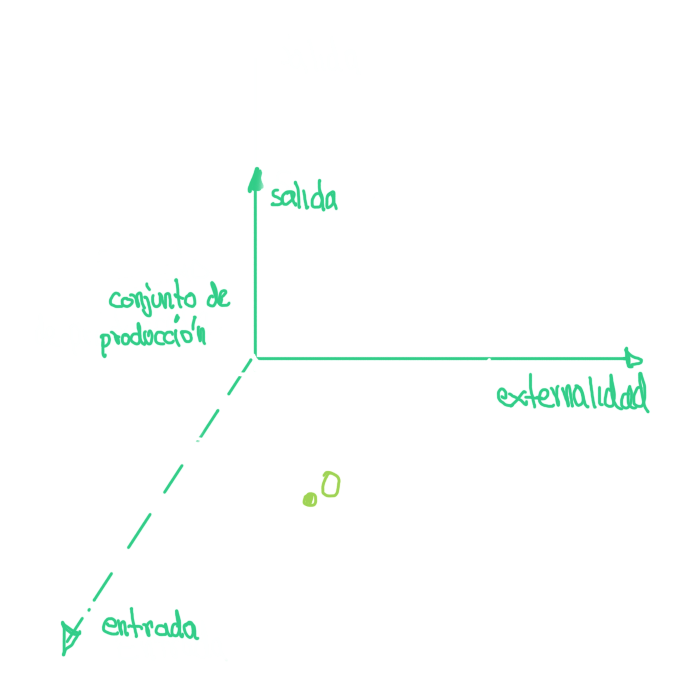
De forma general el nuevo conjunto de consumo depende del ambiente económico \(\left(y^{1}, \ldots, y^{J}, x^{1}, \ldots, x^{i-1}, x^{i+1}, \ldots, x^{I}\right)\)
externalidad
Ejemplo 2
Consumir música es un bien, supongamos que el agente \(j\) lo consume, \(x^j_m\). Entonces la utilidad del agente \(i\)
U^{'i}(\cdot)=U^{i}\left(y^{1}, \ldots, y^{J}, x^{1}, \ldots, x^{i}, \ldots, x^{I}\right)
U^{i}(x^i)
De forma general la nueva utilidad generada por la externalidad depende del ambiente económico \(\left(y^{1}, \ldots, y^{J}, x^{1}, \ldots, x^{i}, \ldots, x^{I}\right)\)
externalidad
U^{'i}(\cdot)=U^{i}\left(x^{i}, x_m^{j}\right)
U^{i}(x^i)
externalidad
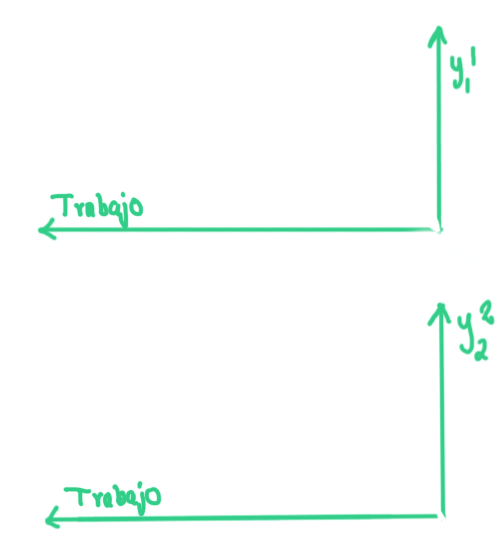
Ejemplo 3
Los bienes,
- Miel \(\equiv y_1^1\)
- Flores \(\equiv y_2^2\)
Meade (1952), apicultor-floricultor
Y^{'j}=Y^{j}\left(y^{1}, \ldots, y^{j-1}, y^{j+1}, \ldots, y^{J}, x^{1}, \ldots, x^{I}\right)
Y^{j}
De forma general el nuevo conjunto de producción depende del ambiente económico \(\left(y^{1}, \ldots, y^{j-1}, y^{j+1}, \ldots, y^{J}, x^{1}, \ldots, x^{I}\right)\)
externalidad
f^{'j}(\cdot)=f^{j}\left(y^{1}, \ldots, y^{j-1}, y^{j}, y^{j+1}, \ldots, y^{J}, x^{1}, \ldots, x^{I}\right)=0
Tal que:
Nota: inicialmente \(f^j(y^j)\)
1.2 Asignación Óptima de Recursos
- Notación
- Economía particular
- Conclusión
Notación
\(X^i \subset \mathbb{R}_+^L\) conjunto de consumo para le consumidor \(i\)
\(L\) número de bienes, \(l=1,\ldots,L\)
\(I\) número de consumidores, \(i=1,\ldots,I\)
\(J\) número de firmas, \(j=1,\dots,J\)
\(x^i=(x_1^i,\ldots,x_L^i )\in X^i\), vector de consumo
\(w^i=(w_1^i,\ldots,w_L^i )\in \mathbb{R}_+^L\), vector de dotación
\(Y^j \subset \mathbb{R}^L\) conjunto de producción para la firma \(j\)
\(y^j=(y_j^i,\ldots,y_L^j )\in Y^j\), vector de producción
\(f^j\), función de producción
\(p \in \mathbb{R}_+^L\), vector de precios
\(p\cdot y^j\), beneficios de la empresa \(j\)
\(\theta^{ij}\in\mathbb{R}_+\), contribución de la firma \(j\) al consumidor \(i\)
\(R^{i}=p\cdot w^i+\sum\limits_j\theta^{ij}p\cdot y^j\), ingreso del consumidor \(i\)
Economía particular
Consideremos una economía con:
- Dos bienes, \(L=2\)
- Dos firmas, \(J=2\)
- Un consumidor, \(I=1\)
Existen dos externalidades:
- Externalidad por consumo \(x_1\)
- Externalidad por producción \(y_1^1\)
Las tecnologías están dadas por:
- \(y_{1}^{1}=f^{1}\left(y_{2}^{1}\right)\)
- \(y_{2}^{2}=f^{2}\left(y_{1}^{2}, y_{1}^{1}, x_{1}\right)\)
\(f^j\) diferenciable y concava
La función de utilidad es:
- \(U(x_1,x_2)\)
\(U\), diferenciable, creciente y estricatmente cuasiconcava
La dotación inicial:
- \(w=(w_1,w_2)\)
El óptimo de Pareto para esta economía se obtiene resolviendo el siguiente problema
\begin{array}{ll}
y_{1}^{1}+y_{1}^{2}+w_{1}-x_{1} \geqslant 0 & \lambda_{1} \\
y_{2}^{1}+y_{2}^{2}+w_{2}-x_{2} \geqslant 0 & \lambda_{2} \\
-y_{1}^{1}+f^{1}\left(y_{2}^{1}\right) \geqslant 0 & \mu_{1} \\
-y_{2}^{2}+f^{2}\left(y_{1}^{2}, y_{1}^{1}, x_{1}\right) \geqslant 0 & \mu_{2}
\end{array}
\operatorname{Max} \, U\left(x_{1}, x_{2}\right)
Sujeto a:
Donde \(\left(\lambda_{1}, \lambda_{2}, \mu_{1}, \mu_{2}\right)\) son los mutiplicadores de Kuhn-Tucker. Se asumen todas las condiciones necesarias para tener soluciones interiores (concavidad, saturación)
\begin{aligned}
\mathcal{L}(\cdot)=& U\left(x_{1}, x_{2}\right)+\lambda_{1}\left(y_{1}^{\prime}+y_{1}^{2}+w_{1}-x_{1}\right)+\lambda_{2}\left(y_{2}^{1}+y_{2}^{2}+w_{2}-x_{2}\right)+\\
& \mu_{1}\left(-y_{1}^{1}+f^{1}\left(y_{2}^{1}\right)\right)+\mu_{2}\left(-y_{2}^{2}+f^{2}\left(y_{1}^{2}, y_{1}^{1}, x_{1}\right)\right.
\end{aligned}
\frac{\partial U}{\partial x_{1}}-\lambda_{1}+\mu_{2} \frac{\partial f^{2}}{\partial x_{1}}=0 \quad\text{(p.1)}\\
\frac{\partial U}{\partial x_{2}}-\lambda_{2}=0\quad\text{(p.2)}
\lambda_{1}-\mu_{1}+\mu_{2} \frac{\partial f^{2}}{\partial y_{1}^{1}}=0 \quad\text{(p.3)}
\lambda_{2}+\mu_{1} \frac{d f^{1}}{d y_{2}^{1}}=0 \quad\text{(p.4)}
\lambda_{2}-\mu_{2}=0\quad\text{(p.5)}
\lambda_{1}+\mu_{2} \frac{\partial f^{2}}{\partial y_{1}^{2}}=0\quad\text{(p.6)}
Se tienen las siguientes condiciones de primer orden
\frac{\frac{\partial U}{\partial x_{1}}+\frac{\partial U}{\partial x_{2}} \cdot \frac{\partial f^{2}}{\partial x_{1}}}{\partial U / \partial x_{2}}=-\frac{\partial f^{2}}{\partial y_{1}^{2}}=-\frac{1+\frac{\partial f^{2}}{\partial y_{1}^{1}} \cdot \frac{d f^{1}}{d y_{2}^{1}}}{d f^{1} / d y_{2}^{1}}
\quad\text{(1)}
Se tienen la igualdad entre las tasas (sociales) marginales de sustitución y transformación
\frac{\frac{\partial U}{\partial x_{1}}+\frac{\partial U}{\partial x_{2}} \cdot \frac{\partial f^{2}}{\partial x_{1}}}{\partial U / \partial x_{2}}
Pigou (1920's): se tienen que tomar en cuenta los efectos directos e indirectos de las actividades económicas
\frac{\frac{\partial U}{\partial x_{1}}+\frac{\partial U}{\partial x_{2}} \cdot \frac{\partial f^{2}}{\partial x_{1}}}{\partial U / \partial x_{2}}=-\frac{\partial f^{2}}{\partial y_{1}^{2}}=-\frac{1+\frac{\partial f^{2}}{\partial y_{1}^{1}} \cdot \frac{d f^{1}}{d y_{2}^{1}}}{d f^{1} / d y_{2}^{1}}
\quad\text{(1)}
Sustituyendo una unidad del bien \(x_1\) por una unidad del bien \(x_2\), la producción del bien dos se ve afectada:
\frac{\partial f^{2}}{\partial x_{1}}
por eso su nivel de utilidad cambia (se agrega)
\frac{\partial U}{\partial x_{2}} \cdot \frac{\partial f^{2}}{\partial x_{1}}
Por lo tanto la tasa (social) marginal de sustitución es
- \(y_{1}^{1}=f^{1}\left(y_{2}^{1}\right)\)
- \(y_{2}^{2}=f^{2}\left(y_{1}^{2}, y_{1}^{1}, x_{1}\right)\)
- \(y_{1}^{1}=f^{1}\left(y_{2}^{1}\right)\)
- \(y_{2}^{2}=f^{2}\left(y_{1}^{2}, y_{1}^{1}, x_{1}\right)\)
-\frac{\partial f^{2}}{\partial y_{1}^{2}}
\frac{\frac{\partial U}{\partial x_{1}}+\frac{\partial U}{\partial x_{2}} \cdot \frac{\partial f^{2}}{\partial x_{1}}}{\partial U / \partial x_{2}}=-\frac{\partial f^{2}}{\partial y_{1}^{2}}=-\frac{1+\frac{\partial f^{2}}{\partial y_{1}^{1}} \cdot \frac{d f^{1}}{d y_{2}^{1}}}{d f^{1} / d y_{2}^{1}}
\quad\text{(1)}
Puesto que la actividad de la firma 2 no crea una externalidad, su tasa (social) marginal de sustitución es igual a su tasa privada
-\frac{1+\frac{\partial f^{2}}{\partial y_{1}^{1}} \cdot \frac{d f^{1}}{d y_{2}^{1}}}{d f^{1} / d y_{2}^{1}}
- \(y_{1}^{1}=f^{1}\left(y_{2}^{1}\right)\)
- \(y_{2}^{2}=f^{2}\left(y_{1}^{2}, y_{1}^{1}, x_{1}\right)\)
\frac{\frac{\partial U}{\partial x_{1}}+\frac{\partial U}{\partial x_{2}} \cdot \frac{\partial f^{2}}{\partial x_{1}}}{\partial U / \partial x_{2}}=-\frac{\partial f^{2}}{\partial y_{1}^{2}}=-\frac{1+\frac{\partial f^{2}}{\partial y_{1}^{1}} \cdot \frac{d f^{1}}{d y_{2}^{1}}}{d f^{1} / d y_{2}^{1}}
\quad\text{(1)}
La firma 1 debe considerar que usando un a unidad adicional del bien 2 como entrada, produce
d f^{1} / d y_{2}^{1}
Consecuentemente afecta la producción del bien 2 por
\frac{\partial f^{2}}{\partial y_{1}^{1}} \cdot \frac{d f^{1}}{d y_{2}^{1}}
de lo cual se sigue que la tasa (social) marginal de transformación esta dada por
La organización óptima de la producción no necesariamente requiere la eliminación total de las externalidades incluso si estas son negativas
Conclusión
- \(y_{1}^{1}=f^{1}\left(y_{2}^{1}\right)\)
- \(y_{2}^{2}=f^{2}\left(y_{1}^{2}, y_{1}^{1}, x_{1}\right)\)
\frac{\frac{\partial U}{\partial x_{1}}+\frac{\partial U}{\partial x_{2}} \cdot \frac{\partial f^{2}}{\partial x_{1}}}{\partial U / \partial x_{2}}=-\frac{\partial f^{2}}{\partial y_{1}^{2}}=-\frac{1+\frac{\partial f^{2}}{\partial y_{1}^{1}} \cdot \frac{d f^{1}}{d y_{2}^{1}}}{d f^{1} / d y_{2}^{1}}
\quad\text{(1)}
Si consumir y producir el bien 1, afecta la producción del bien 2 negativamente. Esto no significa que el bien 1 debe dejar de ser producido en su totalidad. Más bien en la evaluación del costo social del bien 1, los costos externos deben ser internalizados
1.3 Equilibrio Competitivo de Propiedad Privada
- Introducción
- Notación
- Economía particular
- Comentarios
Introducción
El equilibrio competitivo, además de los precios, tendrá como parámetros las variables que generan externalidades. En equilibrio estas variables deben ser iguales a las elegidas por otros agentes.
Notación
\(X^i \subset \mathbb{R}_+^L\) conjunto de consumo para le consumidor \(i\)
\(L\) número de bienes, \(l=1,\ldots,L\)
\(I\) número de consumidores, \(i=1,\ldots,I\)
\(J\) número de firmas, \(j=1,\dots,J\)
\(x^i=(x_1^i,\ldots,x_L^i )\in X^i\), vector de consumo
\(w^i=(w_1^i,\ldots,w_L^i )\in \mathbb{R}_+^L\), vector de dotación
\(Y^j \subset \mathbb{R}^L\) conjunto de producción para la firma \(j\)
\(y^j=(y_j^i,\ldots,y_L^j )\in Y^j\), vector de producción
\(f^j\), función de producción
\(p \in \mathbb{R}_+^L\), vector de precios
\(p\cdot y^j\), beneficios de la empresa \(j\)
\(\theta^{ij}\in\mathbb{R}_+\), contribución de la firma \(j\) al consumidor \(i\)
\(R^{i}=p\cdot w^i+\sum\limits_j\theta^{ij}p\cdot y^j\), ingreso del consumidor \(i\)
Economía particular
Consideremos una economía con:
- Dos bienes, \(L=2\)
- Dos firmas, \(J=2\)
- Un consumidor, \(I=1\)
Existen dos externalidades:
- Externalidad por consumo \(x_1\)
- Externalidad por producción \(y_1^1\)
Las tecnologías están dadas por:
- \(y_{1}^{1}=f^{1}\left(y_{2}^{1}\right)\)
- \(y_{2}^{2}=f^{2}\left(y_{1}^{2}, y_{1}^{1}, x_{1}\right)\)
\(f^j\) diferenciable y concava
La función de utilidad es:
- \(U(x_1,x_2)\)
\(U\), diferenciable, creciente y estricatmente cuasiconcava
La dotación inicial:
- \(w=(w_1,w_2)\)
Vector de precios:
- \(p=(p_1,p_2)\)
Ingreso:
- \(R=p\cdot w+p\cdot y^1+p\cdot y^2\)
El equilibrio ...
Sujeto a:
La firma 1 maximiza sus beneficios, y satisface su nivel de producción. Observemos que no es afectada por externalidades
\operatorname{Max}\left\{p_{1} y_{1}^{1}+p_{2} y_{2}^{1}\right\}
y_{1}^{1}=f^{1}\left(y_{2}^{1}\right)
así se tiene la condición marginal
-\frac{1}{d f^{1} / d y_{2}^{1}\left(y_{2}^{1}\right)}=\frac{p_{1}}{p_{2}}\qquad (2)
El equilibrio ...
Sujeto a:
El consumidor maximiza su utilidad sujeto a su restricción presupuestal
\operatorname{Max}U\left(x_{1}, x_{2}\right)
p_{1} x_{1}+p_{2} x_{2}=R
así se tiene la condición marginal
\frac{\partial U / \partial x_{1}\left(x_{1}, x_{2}\right)}{\partial U / \partial x_{2}\left(x_{1}, x_{2}\right)}=\frac{p_{1}}{p_{2}}\qquad (3)
El equilibrio ...
Sujeto a:
La firma 2 es afectada por las variables dadas del ambiente (enternalidades) \(\bar{x}_1\) y \(\bar{y}_1^1\) elegidas por los otros agentes, así la firma 2 resuelve el problema
\operatorname{Max}\left\{p_{2} y_{2}^{2}+p_{1} y_{1}^{2}\right\}
y_{2}^{2}=f^{2}\left(y_{1}^{2}, \bar{y}_{1}^{1}, \bar{x}_{1}\right)
así se tiene la condición marginal
-\frac{\partial f^{2}}{\partial y_{1}^{2}}\left(y_{1}^{2}, \bar{y}_{1}^{1}, \bar{x}_{1}\right)=\frac{p_{1}}{p_{2}}\qquad (4)
Un equilibrio competitivo con externalidades es un vector de precios \(\left(\bar{p}_{1}, \bar{p}_{2}\right)\) y una asignación \(\left(\bar{x}_{1}, \bar{x}_{2}, \bar{y}_{1}^{1}, \bar{y}_{2}^{1}, \bar{y}_{1}^{2}, \bar{y}_{2}^{2}\right)\) tal que
(a) \(\left(\bar{y}_{1}^{1}, \bar{y}_{2}^{1}\right)\) maximiza \(\bar{p}_{1} y_{1}^{1}+\bar{p}_{2} y_{2}^{1}\) sujeta a \(y_{1}^{1}=f^{1}\left(y_{2}^{1}\right)\)
(b) \(\left(\bar{y}_{1}^{2}, \bar{y}_{2}^{2}\right)\) maximiza \(\bar{p}_{1} y_{1}^{2}+\bar{p}_{2} y_{2}^{2}\) sujeta a \(y_{2}^{2}=f^{2}\left(y_{1}^{2}, \bar{y}_{1}^{1}, \bar{x}_{1}\right)\)
(c) \(\left(\bar{x}_{1}, \bar{x}_{2}\right)\) maximiza \(U\left(x_{1}, x_{2}\right)\) sujeta a \(\bar{p}_{1} x_{1}+\bar{p}_{2} x_{2}=\bar{R}\)
donde \(\bar{R}=\bar{p}_{1} w_{1}+\bar{p}_{2} w_{2}+\Pi(\bar{p})\) y
(d) \( \bar{x}_{1}=w_{1}+\bar{y}_{1}^{1}+\bar{y}_{1}^{2} \)
\( \bar{x}_{2}=w_{2}+\bar{y}_{2}^{1}+\bar{y}_{2}^{2} \)
\(\Pi(\bar{p})=\left(\bar{p}_{1} \bar{y}_{1}^{1}+\bar{p}_{2} \bar{y}_{2}^{1}\right)+\left(\bar{p}_{1} \bar{y}_{1}^{2}+\bar{p}_{2} \bar{y}_{2}^{2}\right)\)
equilibrio en mercados
El interés de cada agente a maximizar lo lleva a igular su tasa privada marginal a la razón de los precios, así las tasas privadas deben ser las mismas. Mientras que el óptimo de Pareto requiere la igualdad de sus tasas sociales.
-\frac{1}{d f^{1} / d y_{2}^{1}\left(y_{2}^{1}\right)}=\frac{\partial U / \partial x_{1}\left(x_{1}, x_{2}\right)}{\partial U / \partial x_{2}\left(x_{1}, x_{2}\right)}=-\frac{\partial f^{2}}{\partial y_{1}^{2}}\left(y_{1}^{2}, \bar{y}_{1}^{1}, \bar{x}_{1}\right)
\frac{\frac{\partial U}{\partial x_{1}}+\frac{\partial U}{\partial x_{2}} \cdot \frac{\partial f^{2}}{\partial x_{1}}}{\partial U / \partial x_{2}}=-\frac{\partial f^{2}}{\partial y_{1}^{2}}=-\frac{1+\frac{\partial f^{2}}{\partial y_{1}^{1}} \cdot \frac{d f^{1}}{d y_{2}^{1}}}{d f^{1} / d y_{2}^{1}}
En general estos equilibrios no son iguales. Observemos que las mismas externalidades pueden llevar a la igualdad de los equilibrio
Social
Privado
Comentarios
- En general las decisiones económicas aparecen muy descentralizadas en un equilibrio competitivo
- Frecuentemente las firmas que producen externalidades negativas producen mucho y las firmas que producen externalidades positivas poco, pero bajo un cierto esquema esto no se ve (ejemplo)
- Observemos que la optimización de los agentes depende de sus propias variables, así las condiciones de existencia (matemáticas) de equilibrio se piden sobre estas.
amazon Todopoderoso
- Externalidad positiva (insumos para su capital) en los productores de acero
- Externalidad negativa (exceso de producción) en el conjunto de producción
- En lugar de pagar impuestos te da puro plátano
- Regulación de competencia
1.4 Tipos de Intervención Pública
- Introducción
- Creación de mercados por medio de la especificación de derechos de propiedad
- Notación
- Impuestos óptimos
- Fusión de firmas
- Abatimiento de la contaminación
Introducción
En el contexto del modelo de Arrow-Debreu en el cual los agentes y mercados están bien definidos pero existen externalidades, estudiamos la intervención del gobierno para restablecer la eficiencia de Pareto, asumiendo que el costo de intervención es cero y sin justificación de la intervención publica
Creación de mercados mediante la especificación de derechos de propiedad
La política económica consisten en establecer un sistema completo de mercados competitivos que incorpore externalidades, con la idea de establecer condiciones similares a las que se tenia antes de la presencia de externalidadedes
La pregunta es la viabilidad de estos mercados
Notación
\(X^i \subset \mathbb{R}_+^L\) conjunto de consumo para le consumidor \(i\)
\(L\) número de bienes, \(l=1,\ldots,L\)
\(I\) número de consumidores, \(i=1,\ldots,I\)
\(J\) número de firmas, \(j=1,\dots,J\)
\(x^i=(x_1^i,\ldots,x_L^i )\in X^i\), vector de consumo
\(w^i=(w_1^i,\ldots,w_L^i )\in \mathbb{R}_+^L\), vector de dotación
\(Y^j \subset \mathbb{R}^L\) conjunto de producción para la firma \(j\)
\(y^j=(y_j^i,\ldots,y_L^j )\in Y^j\), vector de producción
\(f^j\), función de producción
\(p \in \mathbb{R}_+^L\), vector de precios
\(p\cdot y^j\), beneficios de la empresa \(j\)
\(\theta^{ij}\in\mathbb{R}_+\), contribución de la firma \(j\) al consumidor \(i\)
\(R^{i}=p\cdot w^i+\sum\limits_j\theta^{ij}p\cdot y^j\), ingreso del consumidor \(i\)
Economía particular
Consideremos una economía con:
- Dos bienes, \(L=2\)
- Dos firmas, \(J=2\)
- Un consumidor, \(I=1\)
Existen dos externalidades:
- Externalidad por consumo \(x_1\)
- Externalidad por producción \(y_1^1\)
Las tecnologías están dadas por:
- \(y_{1}^{1}=f^{1}\left(y_{2}^{1}\right)\)
- \(y_{2}^{2}=f^{2}\left(y_{1}^{2}, y_{1}^{1}, x_{1}\right)\)
\(f^j\) diferenciable y concava
La función de utilidad es:
- \(U(x_1,x_2)\)
\(U\), diferenciable, creciente y estricatmente cuasiconcava
La dotación inicial:
- \(w=(w_1,w_2)\)
Vector de precios:
- \(p=(p_1,p_2)\)
Ingreso:
- \(R=p\cdot w+p\cdot y^1+p\cdot y^2\)
Precios de los derechos:
- \(q_1^{12}\)
- \(p_1^{12}\)
Cantidad de derechos:
- \(y_1^{12}\)
- \(x_1^{12}\)
- \(\dot y_1^{12}\)
- \(\dot x_1^{12}\)
Supongamos que se crean dos mercados de derechos a contaminar
Sujeto a:
La firma 1 debe comprar a la firma 2 el derecho a contaminar, así el problema de la firma 1 es
\operatorname{Max}\left\{p_{1} y_{1}^{1}+p_{2} y_{2}^{1}-q_1^{12}y_1^{12}\right\}
y_{1}^{1}=f^{1}\left(y_{2}^{1}\right)\\
y_1^{12}=y_1^1
así se tiene la condición primer orden
\left(p_{1}-q_{1}^{12}\right) \frac{d f^{1}}{d y_{2}^{1}}+p_{2}=0\qquad (5)
- \(y_{1}^{1}=f^{1}\left(y_{2}^{1}\right)\)
- \(y_{2}^{2}=f^{2}\left(y_{1}^{2}, y_{1}^{1}, x_{1}\right)\)
Sujeto a:
\operatorname{Max}U\left(x_{1}, x_{2}\right)
p_{1} x_{1}+p_{2} x_{2}+p_1^{12}x_1^{12} =R\\
x_1^{12}=x_1
\frac{\partial \boldsymbol{U} / \partial x_{1}}{\partial \boldsymbol{U} / \partial x_{2}}=\frac{p_{1}+p_{1}^{12}}{p_{2}}\qquad (6)
así se tiene la condición primer orden
El consumidor debe comprar a la firma 2 el derecho a contaminar, así el problema es
- \(y_{1}^{1}=f^{1}\left(y_{2}^{1}\right)\)
- \(y_{2}^{2}=f^{2}\left(y_{1}^{2}, y_{1}^{1}, x_{1}\right)\)
Sujeto a:
La firma 2 oferta las cantidades de los derechos de contaminación \(\dot{x}_1^{12}\) y \(\dot{y}_1^{12}\), así el problema es
\operatorname{Max}\left\{p_{2} y_{2}^{2}+p_{1} y_{1}^{2}+q_1^{12}\dot{y}_{1}^{12}+p_1^{12}\dot{x}_{1}^{12}\right\}
y_{2}^{2}=f^{2}\left(y_{1}^{2}, \dot{y}_{1}^{12}, \dot{x}_{1}^{12}\right)
\begin{array}{l}
p_{2} \frac{\partial f^{2}}{\partial y_{1}^{2}}+p_{1}=0 \\
p_{2} \frac{\partial f^{2}}{\partial y_{1}^{1}}+q_{1}^{12}=0 \\
p_{2} \frac{\partial f^{2}}{\partial x_{1}}+p_{1}^{12}=0
\end{array}\qquad (7)
así se tiene la condiciones de primer orden
Además el equilibrio competitivo requiere la igualdad de la demanda y la oferta de los dos mercados de derechos de contaminación
Combinando las ecuaciones (5), (6), (7) se tiene la condición (1)
El equilibrio competitivo de la economía en la cual el espacio de los bienes ha crecido agregando los mercados de derechos de contaminación es un óptimo de Pareto.
\frac{\frac{\partial U}{\partial x_{1}}+\frac{\partial U}{\partial x_{2}} \cdot \frac{\partial f^{2}}{\partial x_{1}}}{\partial U / \partial x_{2}}=-\frac{\partial f^{2}}{\partial y_{1}^{2}}=-\frac{1+\frac{\partial f^{2}}{\partial y_{1}^{1}} \cdot \frac{d f^{1}}{d y_{2}^{1}}}{d f^{1} / d y_{2}^{1}}
Social
\dot{y}_{1}^{12}=y_{1}^{12} \quad \dot{x}_{1}^{12}=x_{1}^{12}
Observaciones
- En el mercado de derechos de contaminación entre el agente \(i\) y el agente \(j\), solo hay un comprador y un solo vendedor, en consecuencia, el comportamiento competitivo en este mercado es poco probable, y la estrategia puede llevar a un equilibrio menos deseable
- No obstante la política de creación puede ser apropiada en ciertos casos
Varias empresas contaminan un rio (efecto no individual). Una cantidad \(\bar{A}\) se limpia de forma natural, así hay compatibilidad con la natación. \(\bar{A}\) es el nivel socialmente óptimo de contaminación. No hay incentivo de estrategia entre los agentes \(i\) y \(j\) (hay competencia del lado de la demanda). Puede crearse un mercado donde las leyes de la oferta y la demanda determinen un precio a una cantidad de contaminación igual a \(\bar{A}\). Entonces el mercado de derechos de contaminación alcanzará una asignación eficiente (no hay estrategias indivduales)
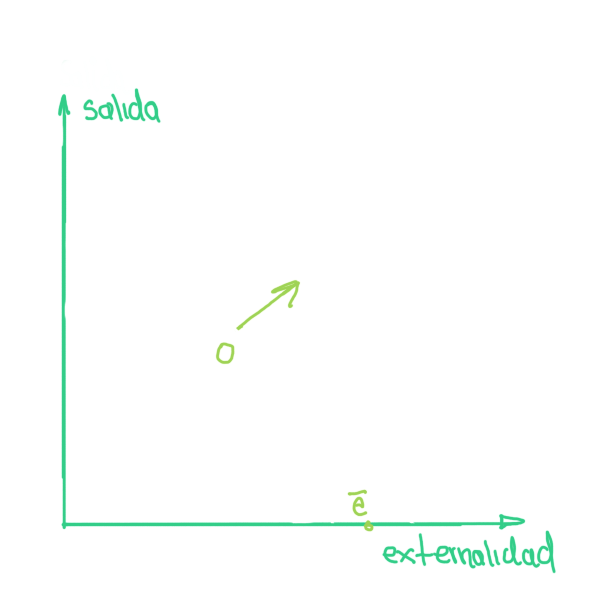
La existencia del equilibrio económico con mercados de derechos de contaminación, requiere las condiciones usuales de convexidad sobre el espacio extendido de bienes
Starrett (1970) (mejor que Laffond )
Sujeto a:
\operatorname{Max}U\left(x_{1}, x_{2}\right)
p_{1} x_{1}+p_{2} x_{2} =R+p_1^{12}\left(\bar{x}-x_1^{12}\right)\\
x_1^{12}=x_1
p_{1} x_{1}+p_{2} x_{2}+p_1^{12}x_1^{12} =R+p_1^{12}\bar{x}
¿Por qué no la firma 2 compra a la firma 1 una reducción en sus niveles de contaminación?
La firma 1 fija a \(\bar{Q}\) su derecho a contaminar y la firma dos puede comprar una reducción a este nivel. Similarmente el consumidor puede asignar su derecho a contaminar a \(\bar x\)
- \(y_{1}^{1}=f^{1}\left(y_{2}^{1}\right)\)
- \(y_{2}^{2}=f^{2}\left(y_{1}^{2}, y_{1}^{1}, x_{1}\right)\)
Las condiciones de marginales son equivalentes a las que se aplican cuando la firma 2 tiene derecho a un ambiente limpio
donde \((\bar x- x_1^{12})\) es la cantidad de reducción de contaminación que oferta
Así la asignación de derechos parece un problema político o un problema de distribución porque esta no afecta el óptimo de Pareto
En general, la cantidad de externalidades que se generan, en la solución eficiente, depende de quien tenga los derechos de propiedad
Existe un caso especial donde el resultado de la externalidad es independiente de quién tenga los derechos de propiedad. SI las preferencias de los agentes son cuasilineales, se genera la misma cantidad de externalidad (caja de Edgeworth)
La conclusión de que en determinadas circunstancias la cantidad eficiente del bien que implica la externalidad es independiente de la distribución de los derechos de propiedad se denomina a veces teorema de Coase
Impuestos Óptimos
Normalizamos los precios \(p_2=1\). Sea \(t\) el pago de impuestos por el consumidor por unidad del bien \(x_1\) consumido. Sea \(\tau\) el pago de impuestos de la firma 1 por unidad de bien \(y_1^1\) producida
La cantidad de los impuestos recabados es redistribuida al consumidor como una transferencia \(T\) de suma fija.
Un equilibrio competitivo con externalidades e impuestos \(t\) y \(\tau\) es un vector de precios \(\left(\bar{p}_{1}, 1\right)\) y una asignación \(\left(\bar{x}_{1}, \bar{x}_{2}, \bar{y}_{1}^{1}, \bar{y}_{2}^{1}, \bar{y}_{1}^{2}, \bar{y}_{2}^{2}\right)\) tal que
(a) \(\left(\bar{y}_{1}^{1}, \bar{y}_{2}^{1}\right)\) maximiza \(\left(\bar{p}_{1}-\tau\right) y_{1}^{1}+ y_{2}^{1}\) sujeta a \(y_{1}^{1}=f^{1}\left(y_{2}^{1}\right)\)
(b) \(\left(\bar{y}_{1}^{2}, \bar{y}_{2}^{2}\right)\) maximiza \(\bar{p}_{1} y_{1}^{2}+ y_{2}^{2}\) sujeta a \(y_{2}^{2}=f^{2}\left(y_{1}^{2}, \bar{y}_{1}^{1}, \bar{x}_{1}\right)\)
(c) \(\left(\bar{x}_{1}, \bar{x}_{2}\right)\) maximiza \(U\left(x_{1}, x_{2}\right)\) sujeta a
\((\bar{p}_{1}+t) x_{1}+ x_{2}=\bar{p}_{1} w_{1}+w_{2}+\bar{T}+\Pi(\bar{p})\); donde
(d) \( \bar{x}_{1}=w_{1}+\bar{y}_{1}^{1}+\bar{y}_{1}^{2} \)
\( \bar{x}_{2}=w_{2}+\bar{y}_{2}^{1}+\bar{y}_{2}^{2} \)
\(\bar{T}=\tau \bar{y}_1^1+t\bar{x}_1\)
equilibrio en mercados
\(\Pi(\bar{p})=(\bar{p}_{1}-\tau) \bar{y}_{1}^{1}+\bar{y}_{2}^{1}+\left(\bar{p}_{1} \bar{y}_{1}^{2}+\bar{y}_{2}^{2}\right)\)
t^{*}=-\frac{\partial f^{2}}{\partial x_{1}}\left(^{*}\right) \quad \tau^{*}=-\frac{\partial f^{2}}{\partial y_{1}^{1}}\left(^{*}\right)
\frac{\partial U / \partial x_{1}}{\partial U / \partial x_{2}}=\bar{\bar{p}{_{1}}}+t^{*}
Los impuestos deben ser elegidos para garantizar el comportamiento de los agentes lleven a un óptimo de Pareto. Se imponen como impuestos los efectos marginales de las actividades que generan externalidad evaluadas en el óptimo \((*)\) obtenido en la sección 1.2
Ahora se usan los precios \((\bar{\bar{p_1}},1)\) del equilibrio competitivo con externalidades asociados con los impuestos anteriores, así las condiciones del consumidor son:
De forma similar para los productores se tiene:
-\frac{1}{d f^{1} / d y_{2}^{1}}=\bar{\bar{p}}_{1}-\tau^{*} \quad-\frac{\partial f^{2}}{\partial y_{1}^{2}}=\bar{\bar{p}}_{1}
\frac{\lambda_{1}}{\lambda_{2}}=\bar{\bar{p}}_{1}=\frac{\frac{\partial U}{\partial x_{1}}(*)+\frac{\partial U}{\partial x_{2}}(*) \cdot \frac{\partial f^{2}}{\partial x_{1}}(*)}{\partial U / \partial x_{2}(*)}=-\frac{\partial f^{2}}{\partial y_{1}^{2}}\left(^{*}\right)=-\frac{1+\frac{d f^{2}}{d y_{1}^{1}}(*) \cdot \frac{d f^{1}}{d y_{2}^{1}}(*)}{d f^{1} / d y_{2}^{1}(*)}
De lo anterior se llega a la siguiente igualdad, al comparar con la expresión del óptimo de Pareto (sección 1.2) se tiene que el óptimo de Pareto será un equilibrio competitivo para los precios \((\bar{\bar{p_1}},1)\)
Si la función de producción de la firma 2, es estrictamente cóncava en \(y_1^2\), y \(y_1^{*1},x_1^*\) son considerados parámetros, la firma elige \((y_1^{*2},y_2^{*2})\)
Los argumentos de lo anterior, son sobre unicidad de soluciones, es decir:
Si la función de producción de la firma 1, es estrictamente cóncava en \(y_2^1\), la firma elige \((y_1^{*1},y_2^{*1})\)
\bar{\bar{p}}_{1}=-\frac{\partial f^{2}}{\partial y_{1}^{2}}(y_{1}^{* 2})
\bar{\bar{p}}_{1}=-\frac{1}{\partial f^{1} / \partial y_{2}^{1}(*)}-\frac{\partial f^{2}}{\partial y_{1}^{1}}(*)
\bar{\bar{p}}_{1}=\frac{\partial U / \partial x_{1}(*)}{\hat{\partial} U / \partial x_{2}(*)}+\frac{\partial f^{2}}{\partial x_{1}}(*)
Si la función de utilidad, es estrictamente cuasi-cóncava, el consumidor elige \(x_1^*, x_2^*\)
Observaciones:
- La sección donde optimiza la firma 2 es covexa si se tienen una función de producción con retornos a escala no crecientes para cada valor de las variables ambientales (externalidades)
- Con esta política tributaria, los agentes que son afectados por la contaminación no necesariamente son compensados por todos los daños (depende de la carga de impuestos). En general el monto de los impuestos recaudados no es igual a los daños ocasionados
- Se asume que las unidades de contaminación pueden ser observadas
- Puede agregarse una penalización para desmotivar que se oculte información respecto a la externalidad (observarla)
Fusión de firmas
\frac{\partial {f}^{2}}{\partial x_{1}} \equiv 0
Sujeto a:
\operatorname{Max}\left\{p_{1} y_{1}^{1}+p_{2} y_{2}^{1}+p_{2} y_{2}^{2}+p_{1} y_{1}^{2}\right\}
y_{1}^{1}=f^{1}\left(y_{2}^{1}\right)\\
y_2^{2}=f^2\left(y_1^2,y_1^1\right)
p_{1} \frac{\partial f^{1}}{\partial y_{2}^{1}}+p_{2} \frac{\partial f^{2}}{\partial y_{1}^{1}} \cdot \frac{d f^{1}}{d y_{2}^{1}}+p_{2}=0
p_{2} \frac{\partial f^{2}}{\partial y_{1}^{2}}+p_{1}=0
Consideremos que solo la firma 1 contamina a la firma 2
Integrando ambas firmas en un problema de optimización conjunta de beneficios
Las condiciones de primer orden
\frac{p_{1}}{p_{2}}=-\frac{\partial f^{2}}{\partial y_{1}^{2}}=-\frac{1+\frac{\partial f^{2}}{\partial y_{1}^{1}} \cdot \frac{\partial f^{1}}{\partial y_{2}^{1}}}{d f^{1} / d y_{2}^{1}}
Entonces el equilibrio competitivo es Pareto óptimo. Ambas firmas están interesadas en fusionarse, porque sus beneficios aumentan, tomando los precios como parámetros dados. Si las empresas no son lo suficientemente pequeñas, los precios pueden alterarse por la fusión y así esta opción no sería la conveniente
Abatimiento de la contaminación
z=\phi\left(y_{1}^{1}, d\right) \quad \text { con } \quad \phi\left(y_{1}^{1}, 0\right) \equiv y_{1}^{1}
Tiene el objetivo de eliminar o disminuir el nivel de contaminación y al mismo tiempo mantener el nivel de la actividad que genera la externalidad
Se considera el problema da la sección 1.2 (Pareto), además se considera que solo la firma 1 genera una externalidad en la firma 2.
Sea \(z\) la cantidad de contaminación. En la ausencia de abatimiento de contaminación \(z=y_1^1\), por ahora se supondrá que la firma 1 modifica esta cantidad mediante un gasto \(d\) del bien \(y_1\)
\begin{array}{ll}
y_{1}^{1}+y_{1}^{2}+w_{1}-x_{1}-d \geqslant 0 & \lambda_{1} \\
y_{2}^{1}+y_{2}^{2}+w_{2}-x_{2} \geqslant 0 & \lambda_{2} \\
-y_{1}^{1}+f^{1}\left(y_{2}^{1}\right) \geqslant 0 & \mu_{1} \\
-y_{2}^{2}+f^{2}\left(y_{1}^{2}, \phi(y_1^1,d)\right) \geqslant 0 & \mu_{2}
\end{array}
\operatorname{Max} \, U\left(x_{1}, x_{2}\right)
Sujeto a:
El problema de optimización para el consumidor:
Simplificando estas condiciones de primer orden se tiene
\frac{
\frac{\partial U}{\partial x_1} }
{
\frac{\partial U}{\partial x_{2}}}
=-\frac{\partial f^{2}}{\partial y_{1}^{2}}=\frac{\partial f^{2}}{\partial z} \cdot \frac{\partial \phi}{\partial d}=-\frac{1+\frac{\partial f^{2}}{\partial z} \cdot \frac{d f^{1}}{d y_{2}^{1}} \cdot \frac{\partial \phi}{\partial y_{1}^{1}}}{\frac{d f^{1}}{d y_{2}^{1}}}
\tau^{*}=-p_{2}^{*} \cdot \frac{\partial f^{2}}{\partial z}\left(^{*}\right)
Con esta técnica se tiene que igualar la productividad marginal de una unidad del bien 1 utilizada en el abatimiento de la contaminación
\frac{\partial f^{2}}{\partial z} \cdot \frac{\partial \phi}{\partial d}
Con la productividad marginal de una unidad del bien 1 utilizada en la producción del bien 2
-\frac{\partial f^{2}}{\partial y_{1}^{2}}
directamente, se pueden cobrar impuestos a la contaminación a la tasa
\operatorname{Max}\left\{p_{1}^{*} y_{1}^{1}+p_{2}^{*} y_{2}^{1}-\tau^{*} z+p_{1}^{*} d\right\}
Sujeto a:
\begin{aligned}
-y_{1}^{1}+f^{1}\left(y_{2}^{1}\right) & \geqslant 0 \\
z-\phi\left(y_{1}^{1}, d\right) & \geqslant 0
\end{aligned}
la firma puede elegir libremente sus niveles de abatimiento de contaminación y su nivel de actividad. Entonces la firma resuelve el problema
Para las cuales se obtienen las condiciones de primer orden del óptimo de pareto
¿El libro tiene un
error de dedo?
\tau^{*}=-p_{2}^{*} \cdot \frac{\partial f^{2}}{\partial z}\left(^{*}\right)
p_{1}^{*} \bar{d}=\tau^{*} z^{*} \quad \bar{d}=z^{*} \frac{\partial f^{2} / \partial z\left(^{*}\right)}{\partial f^{2} / \partial y_{1}^{2}\left(^{*}\right)}
Se pueden considerar combinar las políticas descritas. Cobrar impuestos a los contaminadores y subsidiar el abatimiento de la contaminación.
Sea \(\bar{d}\) la cantidad de abatimiento de contaminación subsidiada, con un argumento similar al anterior desarrollado, para cualquier \(\bar{d}\) se tiene
y con esto las condiciones de óptimo de Pareto. Para el banace del presupuesto es suficiente elegir \(\bar{d}\) tal que
que será positiva si \(\bar{d}\leq d^*\) (Kolm 1975)
1.5 Conclusiones
Podemos asociar un mercado de derechos de propiedad. Sin embargo cuestiones técnicas (no convexidad) podrían llevarnos a que no existe equilibrio con este planteamiento
Como segunda forma de descentralizar, la implementación de impuestos, matemáticamente (convexidad), en principio, es más viable, además los impuestos los fija el gobierno (competencia), la debilidad es la información sobre la contaminación. Este enfoque crea déficits o superávits presupuestarios que se aborda haciendo transferencias de suma fija apropiadas.
El gobierno puede fomentar la creación de información especifica, inducir la competencia y así resolver varios problemas de externalidades.
Argumento: Los agentes serán los más interesados en ajustar su actividades para internalizar sus externalidades, así descartarán la fuente de ineficiencia tan pronto como la información este disponible. En un régimen de competencia pura y perfecta las externalidades de internalizarán naturalmente
Por lo tanto las justificaciones de intervención del gobierno deben buscarse en lo siguiente
- Ventajas de información y organización
- El mal funcionamiento de la entrada libre (costos)
- Utilizar la política ambiental como herramienta redistributiva
1.6 La compatibilidad de los Retornos Crecientes y la Competencia Perfecta
y_{1}^{1} \leqslant y_{2}^{1} \cdot y_{2}^{2} \quad y_{1}^{2} \leqslant y_{2}^{2} \cdot y_{2}^{1}
\left\{\left(z_{1}, z_{2}\right): z_{1} \leqslant 2 y_{2}^{1} \cdot y_{2}^{2}, z_{2}=y_{2}^{1}+y_{2}^{2}\right\}
Consideremos dos firmas que exhiben una tecnología de retornos constantes a escala cuando cada una considera la salida de la otra como un parámetro, pero exhibe retornos globales crecientes cuando ambas salidas son variables. Ambas firmas producen el bien 1 y usan el bien 2 como entrada de acuerdo a las siguientes técnologias
El conjunto agregado de producción es el siguiente:
Si procedemos como la sección 1.3 encontraremos un equilibrio competitivo con externalidades
z_1=(z_2)^2/2
\operatorname{Max}\left\{y_{2}^{1} \cdot y_{2}^{2}+y_{2}^{2} \cdot y_{2}^{1}\right\}=2 y_{2}^{1} y_{2}^{2}
y_2^1 + y_2^2=z_2
Sujeto a:
La máxima producción del bien 1 (\(z_1\)), para una cantidad disponible del bien 2 (\(z_2\))
El libro tiene un
error de dedo
Así la función de producción agregada
Los retornos crecientes son compatibles con un equilibrio con externalidades. Sin embargo mezclar las dos firmas para eliminar la ineficiencia excluye la existencia de un equilibrio competitivo por la no convexidad de la función de producción agregada (Capítulo 3 )
1.7 Externalidades y Teoría de Juegos
La presencia de externalidades introduce dificultad de representación de una economía de intercambio como un juego.
\(\alpha\)-core. Conjunto de asignaciones que no pueden ser bloqueadas por ninguna coalición
Bloqueo de asignación-\(\alpha\) por coalición. Una coalición bloquea una asignación si es posible elegir actividades que produzcan una mejora sobre la asignación propuesta para cada uno de sus miembros, independientemente de las acciones de aquellos ajenos a la coalición
Que una coalición pueda realizarse depende (debido a las externalidades) de las acciones de los agentes que no están en dicha coalición.
\(\beta\)-core. Conjunto de asignaciones que no pueden ser bloqueadas por ninguna coalición
Bloqueo de asignación-\(\beta\) por coalición. Una coalición bloquea una asignación si, sin importar las acciones fuera de los agentes de la coalición, la coalición tiene una estrategia de respuesta que asegura mejorar la situación inicial de todos sus miembros
\sum\limits_{i=1}^{3} x^{j i}=1\;\; \forall j
u^{i}=-\sum\limits_{j=1}^{3} x^{j i}+\sum\limits_{j=1}^{3} z^{j i}
Consideremos en siguiente ejemplo (Shapley y Shubik (1969)). Tres jugadores con una unidad de basura, \(x^{ji}\) es la cantidad de basura que el jugador \(j\) arroja (no puede regresarse) en el área del jugador \(i\) tal que
Cada agente tiene una unidad de dinero; \(z^{ji}\) es la cantidad de dinero entregada por el agente \(j\) al agente \(i\). La utilidad del agente \(i\) es dada por
Se tiene que: \(\beta\)-core \(\subset\) \(\alpha\)-core, el \(\beta\)-core puede ser vacia cuando el \(\alpha\)-core no lo es
\text{(a)}\;\,u^{i} \geqslant-1 \quad \forall i \in I
\text{(a)} \;\, u^{i} \geq -1, \;\; i \in\{1,2,3\}=I
El \(\beta\)-core es vació; pues una asignación \(\beta\)-core debe satisfacer
\text{(b)} \;\, u^{i} \geq \frac{1}{2}, \quad u^{j} \geq \frac{1}{2} \quad \forall(i j) \in I \times I, \quad i \neq j
\text{(c)} \;\, u^{1}+u^{2}+u^{3}=0
Para no ser bloqueada por ninguna coalición. Sin embargo (b) contradice (c). Ahora el \(\alpha\)-core requiere que
\text{(b)}\;\, u^{i} \geqslant 0 \;\;\forall i \in I\\
\text{(c)}\;\, u^{1}+u^{2}+u^{3}=0
La coalición de dos jugadores, digamos 1 y 2, ya no puede reaccionar a la estrategia del agente 3 mediante una reasignación de dinero
En el \(\beta\)-core, si el agente 3 arroja su basura al agente 1, el agente 2 quizás le de la mitad de su dinero, así cada agente recibe utilidad de \(1/2\).
En el \(\alpha\)-core, el dinero puede ser distribuido antes de que se conozca donde arrojará su basura el agente 3. Así, solo se puede garantizar una utilidad de nivel 0 (+1 de la dotación de dinero, -1 de arrojar la basura el agente 3)
1.8 Una Rehabilitación de las Externalidades Pecuniarias
No se han incluido las externalidades pecuniarias.
Caso 1. Cualquier cambio en el comportamiento de consumo o producción de un agente influye en los precios sin crear problemas de asignación cuando todos los agentes se compartan de manera competitiva, los precios juegan el papel de igualar oferta y demanda. Así se tiene un óptimo de Pareto (con un sistema de mercados completo sin asimetrías), así las externalidades pecuniarias son irrelevantes.
Cuando se deja el esquema de Arrow-Debreu, los precios generan problemas de eficiencia incluso en una economía competitiva
Caso 2. Cuando la información es descentralizada, los precios también transmiten un tipo de información. Así cualquier acción de un agente que altere los precios, cambia la utilidad esperada de otros agentes (Externalidad informal por medio de precios)
Si los mercado son incompletos, sucede que un agente por su influencia en precios afecta el conjunto de consumo de otros agentes (Externalidad dimensional por medio de precios)
Si hay retornos crecientes, sucede que la acción de un agente por su influencia en los precios afecta el ingreso ( Externalidad de distribución por medio de precios)
La noción de externalidad pecuniaria lleva a la descripción de diferentes tipos de ineficiencia que crea potenciales intervenciones gubernamentales.
Copy of Ecomía Pública: Externalidades
By ra_fa
Copy of Ecomía Pública: Externalidades
Se presenta el tema de externalidades
