Control
Dr. Rafael Martínez Martínez
Los autores han hecho su mejor esfuerza en la preparación de este material. Se distribuye gratuitamente con la esperanza de que sea útil, pero sin ninguna garantía expresa o implícita respecto a la exactitud o completitud del contenido.

Conceptos de sistemas
Señal, sistema
Subtitle
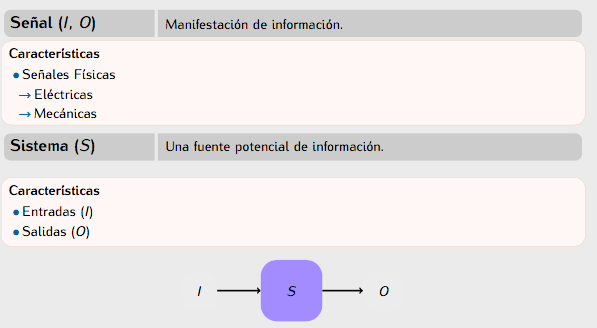
La definición se toma de [1]
Experimento, modelo
Subtitle

La definición se toma de [1]
Simulación
Subtitle

La definición se toma de [1]
Problema: directo, inverso y de control
Subtitle

La definición se toma de [1]
Observaciones
En señales y sistemas nos interesa el problema directo. Es decir encontramos la salida dados la entrada y el sistema, donde las entradas y salidas las modelamos como funciones matemáticas dependientes del tiempo y el sistema es un modelo matemático, en nuestro caso, una ecuación entre la entrada y la salida.
Ejemplos:
La entrada suele ser manipulada (se puede elegir, en general será relativamente obvia) y esta dependerá de la naturaleza del sistema (eléctrico, mecánico, etc) o de una manipulación que se haga al sistema (problema de control). La salida en ocasiones puede elegirse, aunque la mayor parte de las ocasiones esta restringida (por ejemplo: motores).
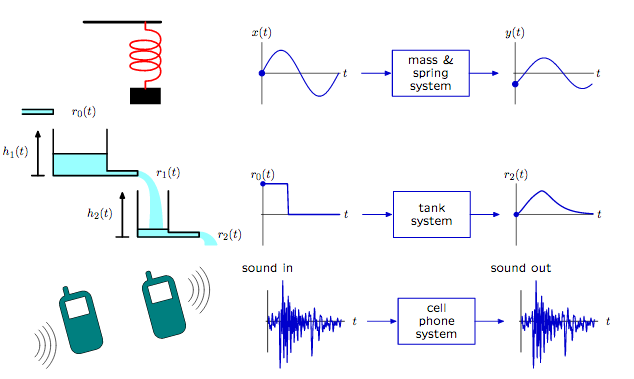
La figura se toma de [2]
Abstracción de sistemas y modelos
Sistemas como transformaciones de señales
Para un sistema
y(t)=\sum\{x(t)\}
denotamos la salida o respuesta con
\sum
y(t)
x(t)
asociada a la entrada
como:
Es decir, cada entrada produce una salida, si cambia la entrada, cambia la salida, (un sistema es una función de funciones). De aquí se deriva la siguiente convención, si la entrada es una función exponencial la salida recibe el nombre de respuesta a la función exponencial. Si la entrada es un escalón, la salida recibe el nombre de respuesta al escalón. Si la entrada es un impulso (delta de Dirac ), la salida recibe el nombre de respuesta al impulso, etc.
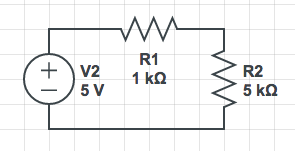
Modelo entrada-salida: Sistemas eléctricos
y(t)=\frac{R_i}{R_1+R_2}x(t)
\sum
-
Usamos la ley fundamental del sistema
-
Escribimos las relaciones entre los componentes del sistema
-
Substituimos todas las variables por entradas y salidas (mediante las relaciones)
-
Escribimos a la salida en términos de la entrada (implícita o explícitamente)
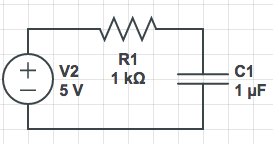

\sum

y(t)=y(t_0)e^{-\frac{1}{CR}(t-t_0)}+\frac{1}{CR}\int_{t_0}^{t}x(\tau)e^{-1/RC(t-\tau)}\,d\tau,\;t\geq t_0
y(t)=\left(y(t_0)e^{-\frac{1}{CR}(t-t_0)}+x(t)*\frac{1}{CR}e^{-(1/RC)
t}\right)u(t-t_0)
\frac{d}{dt}y(t)+\frac{1}{CR}y(t)=\frac{1}{CR}x(t)
salida el voltaje en el resistencia
salida el voltaje en capacitor
Modelo entrada-salida: Sistemas eléctricos
-
Observamos que las relaciones entrada y salida son de diferente complejidad
-
En algunos sistemas se necesita más información para conocer la salida (condiciones iniciales)
-
El modelo cambia dependiendo cual sea el objeto de estudio o por restricciones del mismo sistema (motores)
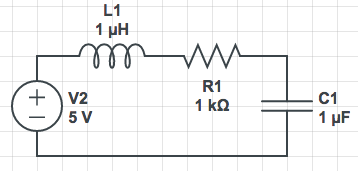
\sum

\frac{d^2}{dt^2}y(t)+\frac{R}{L}\frac{d}{dt}y(t)+\frac{1}{LC}y(t)=\frac{1}{L}\frac{d}{dt}x(t)
salida la corriente del circuito
\frac{d^2}{dt^2}y(t)+\frac{R}{L}\frac{d}{dt}y(t)+\frac{1}{LC}y(t)=\frac{1}{LC}x(t)
salida el voltaje en el capacitor
Clasificación y propiedades de sistemas
Clasificación de los sistemas
De acuerdo al número de entradas y salidas
-
SISO (Single Input Single Output)
-
MIMO (Multiple Input Multiple Output)
-
SIMO
-
MISO
De acuerdo al tipo de señal de entrada y salida
-
Continuos. Entrada y salida en tiempo continuo
-
Discretos. Entrada y salida en tiempo discreto
-
Analógicos. Entrada y salida analogica
-
Digitales. Entrada y salida digital.
-
Híbridos. Combinación de los anteriores
Existen otras clasificaciones de los sistemas (causales, con memoria, lineales, variantes en el tiempo, parámetros concentrados, invertibles, estables, etc. ), en particular las propiedades de Linealidad e Invariancia en Tiempo (LTI) son importantes, pues los sistemas que satisfagan estas definiciones permiten describir su salida como una transformación especifica de la entrada (una convolución).
Memoria de un sistema
Cuando la salida solo dependa de la entrada en el mismo instante de tiempo diremos que no tiene memoria (o que es instantáneo).
Se dice que un sistema tiene memoria (o es dinámico) si la salida en un determinado tiempo depende necesariamente de la entrada en tiempos anteriores o posteriores a él.
y(T_0)=\sum\{x(t)\},\;\;t\leq T_0\;o\;t\geq T_0


\sum
\sum
Causalidad de un sistema
Decimos que un sistema es causal (o no anticipante) si al querer conocer la salida en un determinado tiempo, solo depende de la entrada en ese tiempo o anteriores a el, en términos de ecuaciones
y(T_0)=\sum\{x(t)\},\;\;t\leq T_0
En caso contrario diremos que el sistema es no causal o anticipante. Esta propiedad dice que no puede existir salida sin una entrada en el sistema.


\sum
\sum
Invariancia en tiempo de un sistema (TI)
Si se tiene que la respuesta para la entrada
Se conoce la respuesta de un sistema
dada una entrada
y_1(t)=\sum\{x_1(t)\}
\sum
x_2(t)=x_1(t-T_0)
es
y_2(t)=y_1(t-T_0)
es decir, si al trasladar la entrada en tiempo se produce
la misma traslación en la salida, se dirá que el sistema es invariante en tiempo, en caso contrario se dirá que es variante en tiempo

\sum
Linealidad de un sistema (L)
Si se tiene que la respuesta para la entrada
\sum\left(ax(t)\right)=a\sum\{x(t)\}
Se conoce la respuesta de un sistema
dada una entrada
y_1(t)=\sum\{x_1(t)\}
\sum
x_2(t)=ax_1(t)
Sistema homogeneo
es
y_2(t)=ay_1(t)
es decir, si al escalar la entrada se produce el mismo escalamiento en la salida, se dirá que el sistema es homogéneo en caso contrario el sistema será no homogeneo


\sum
\sum
Linealidad de un sistema (L)
Si se tiene que la respuesta para la entrada
Se conocen las respuestas de un sistema
dadas dos entradas
y_1(t)=\sum\{x_1(t)\}
\sum
y_2(t)=\sum\{x_2(t)\}
x_3(t)=x_1(t)+x_2(t)
Sistema aditivo
es
y_3(t)=y_1(t)+y_2(t)
es decir, si al sumar entradas la salida es la suma de
\sum\{x_1(t)+x_2(t)\}=\sum\{x_1(t)\}+\sum\{x_2(t)\}
las respuestas correspondientes, se dirá que el sistema es aditivo, en caso contrario el sistema no será aditivo.



\sum
\sum
\sum
Linealidad de un sistema (L)
Se dice que un sistema es lineal si es homogéneo y aditivo.
Como ejemplo: los circuitos eléctricos comunes de resistencias y fuentes son lineales, una metodología de solución consiste en aplicar el método de superposición, que consiste en calcular los efectos de las fuentes en el elemento deseado de manera independiente y posteriormente sumar todos las respuestas.
Ejemplos: Propiedades de sistemas
Para los siguientes sistemas revisar:
-
Causalidad
-
Memoria
-
Invariancia en tiempo
-
Linealidad
-
Respuesta al escalón
-
Respuesta al impulso
1)\;y(t)=y(t_0)e^{-\frac{1}{CR}(t-t_0)}+\frac{1}{CR}\int_{t_0}^{t}x(\tau)e^{-1/RC(t-\tau)}\,d\tau,\;t\geq t_0
2)\;y(t)=\frac{1}{CR}\int_{t_0}^{t}x(\tau)e^{-1/RC(t-\tau)}\,d\tau,\;t\geq t_0
3)\;y[n]=x[n-2]
4)\;y[n]=nx[n-2]
5)\;y(t)=\frac{d}{dt}x(t)
6)\;y(t)=x(t)
Sistemas LTI continuos y álgebra de bloques
Respuesta de los sistemas LTI continuos
\sum

\sum

\delta(t)
h(t)
x(t)
y_x(t)
Entrada trasladada produce salida trasladada (TI)
\sum

\delta(t-n\Delta\tau)
h(t-n\Delta\tau)
\sum

x(n\Delta\tau)\Delta\tau\delta(t-n\Delta\tau)
x(n\Delta\tau)\Delta\tau h(t-n\Delta\tau)
Entrada escalada produce salida escalada (L)
La idea es escribir cualquier entrada en términos de deltas
Respuesta de los sistemas LTI continuos
\displaystyle
\begin{array}{l}
x(t)\approx\ldots+x(-\Delta\tau)(u(t+\Delta\tau)-u(t))+x(0)(u(t)-u(t-\Delta\tau))+x(\Delta\tau)(u(t-\Delta\tau)-u(t-2\Delta\tau))\\
+\ldots+x(n\Delta\tau)(u(t-n\Delta\tau)-u(t-(n+1)\Delta\tau))\\
=\ldots+x(-\Delta\tau)\frac{u(t+\Delta\tau)-u(t)}{\Delta\tau}\Delta\tau+x(0)\frac{u(t)-u(t-\Delta\tau)}{\Delta\tau}\Delta\tau+x(\Delta\tau)\frac{u(t-\Delta\tau)-u(t-2\Delta\tau)}{\Delta\tau}\Delta\tau\\
+\ldots+x(n\Delta\tau)\frac{u(t-n\Delta\tau)-u(t-(n+1)\Delta\tau)}{\Delta\tau}\Delta\tau
\end{array}
\displaystyle x(t)=\lim_{\Delta\tau\to 0}\sum_{n=-\infty}^{\infty}\displaystyle x(n\Delta\tau)\frac{u(t-n\Delta\tau)-u(t-(n+1)\Delta\tau)}{\Delta\tau}\Delta\tau
Observemos la geometría de la siguiente aproximación
Entonces se puede escribir a la señal de entrada como
\displaystyle x(t)=\lim_{\Delta\tau\to 0}\sum_{n=-\infty}^{\infty}\displaystyle x(n\Delta\tau)\Delta\tau \delta(t-n\Delta\tau)
\sum

\displaystyle \lim_{\Delta\tau\to 0}\sum_{n=-\infty}^{\infty}\displaystyle x(n\Delta\tau)\Delta\tau \delta(t-n\Delta\tau)
\displaystyle \lim_{\Delta\tau\to 0}\sum_{n=-\infty}^{\infty} x(n\Delta\tau)\Delta\tau h(t-n\Delta\tau)
Suma de entradas produce suma de salidas (L)
Respuesta de los sistemas LTI continuos
\sum

\displaystyle \lim_{\Delta\tau\to 0}\sum_{n=-\infty}^{\infty}\displaystyle x(n\Delta\tau)\Delta\tau \delta(t-n\Delta\tau)
\displaystyle \lim_{\Delta\tau\to 0}\sum_{n=-\infty}^{\infty} x(n\Delta\tau)\Delta\tau h(t-n\Delta\tau)
\sum

\displaystyle \int_{-\infty}^{\infty}x(\tau)\delta(t-\tau)\,d\tau
\displaystyle \int_{-\infty}^{\infty}x(\tau)h(t-\tau)\,d\tau
\sum

\displaystyle x(t)
\displaystyle y_x(t)=x(\tau)*h(t)
\displaystyle y_x(t)=x(t)*h(t)
La salida de todo sistema LTI continuo es una convolución de la entrada con la respuesta al impulso del sistema
Nota
-
La transformada de Laplace bilateral y unitateral derecha de una convolución es el producto de las transformadas
-
La convolución de señales causales es causal
\displaystyle x(t)*h(t)=\int_{-\infty}^{\infty}x(\tau)h(t-\tau)\,d\tau
\displaystyle x(t)*h(t)=\int_{0}^{t}x(\tau)h(t-\tau)\,d\tau
Notación de bloques para un sistema LTI
x(t)
\displaystyle y(t)=x(t)*h(t)
Por el resultado anterior, puede dotarse de una operatividad al esquema que se ha utilizado para los sistemas, es decir, dado un sistema, este puede ser representado por su respuesta al impulso y así definir un "álgebra" de sistemas, que normalmente se conoce como álgebra de bloques, que nos ayuda a visualizar el flujo de información entre los sistemas
h(t)

\sum
y(t)
x(t)
y(t)
Si tenemos un bloque (sistema) se genera una ecuación donde la señal de la linea de salida es la convolución entre el contenido del bloque y la señal de linea de entrada.
De manera similar si tenemos una ecuación de convolución podemos generar un bloque donde una de las señales se asocia al bloque y otra a la linea de entrada.
X(s)
\displaystyle Y(s)=X(s)H(s)
H(s)

Y(s)
Si aplicamos trasformada de Laplace
Entonces la idea de "álgebra de bloques" tiene una mejor semántica pues la transformación de la señal de entrada en la señal de salida se hace mediante una multiplicación. Observamos que en este sentido un bloque puede ser convertido en una ecuación de multiplicación, y una ecuación de multiplicación en un bloque. Observamos los siguientes hechos:
Segunda definición: Transformada de Laplace de la salida del sistema entre la transformada de Laplace de la entrada del sistema
\displaystyle H(s)=\mathscr{L}\{h(t)\}
\displaystyle H(s)=\frac{Y(s)}{X(s)}
H(s) se denomina FUNCIÓN DE TRANSFERENCIA del sistema
Primer definición: Transformada de Laplace de la respuesta al impulso del sistema
¿Por qué el nombre de función de transferencia?, basta observar el bloque o la ecuación de convolución.
Los sistemas pueden interactuar entre si dando lugar a nuevos sistemas y así a una nueve función de transferencia que representa a este nuevo sistema. A continuación describiremos tres interconexiones usuales entre los sistemas: serie, paralelo y retroalimentación, obtendremos las funciones de transferencia de estos nuevos sistemas mediante el álgebra de bloques discutida anteriormente.
Función de transferencia para un sistema diferencial
Aplicamos transformada de Laplace
condiciónes iniciales
a_nD^ny(t)+\ldots+a_1Dy(t)+a_0y(t)=b_mD^mx(t)+\ldots+b_1Dx(t)+b_0x(t)
y(0^-)=\dot{y}(0^-)=\ldots=\dot{y}^{(n-1)}(0^-)=0
\displaystyle a_ns^nY(s)+\ldots+a_1sY(s)+a_0Y(s)=b_ms^mX(s)+\ldots+b_1sX(s)+b_0X(s)
\displaystyle \frac{Y(s)}{X(s)}=\frac{b_ms^m+\ldots+b_1s+b_0}{a_ns^n+\ldots+a_1s+a_0}=\frac{P(s)}{Q(s)}=H(s)
x(0^-)=\dot{x}(0^-)=\ldots=\dot{x}^{(m-1)}(0^-)=0
Conexiones de sistemas

\displaystyle
\begin{array}{l}
Y(s)=X(s)H_1(s)\\
Z(s)=V(s)H_2(s)
\end{array}
H_1(s)
X(s)
Y(s)

H_2(s)
V(s)
Z(s)
Serie


Z(s)

H_1(s)H_2(s)
X(s)
X(s)
Y(s)=V(s)
H_1(s)
H_2(s)
\displaystyle
\begin{array}{l}
Y(s)=V(s)\\
Z(s)=X(s)H_1(s)H_2(s)
\end{array}
Z(s)
¿Con notación de convolución?
Conexiones de sistemas

\begin{array}{l}
Y_1(s)=X(s)H_1(s)\\
Y_2(s)=X(s)H_2(s)
\end{array}
H_1(s)

H_2(s)
Paralelo


Z(s)

H_1(s)+H_2(s)
X(s)
X(s)
H_1(s)
H_2(s)
\displaystyle
\begin{array}{l}
Z(s)=Y_1(s)+Y_2(s)\\
Z(s)=X(s)(H_1(s)+H_2(s))
\end{array}
Z(s)
¿Con notación de convolución?
Y_1(s)
Y_2(s)
Conexiones de sistemas

\displaystyle
\begin{array}{l}
Z(s)=V(s)H_1(s)\\
V(s)=X(s)\mp Z(s)H_2(s)
\end{array}
H_1(s)

H_2(s)
Retroalimentación

Z(s)

\displaystyle
\frac{H_1(s)}{1\pm H_1(s)H_2(s)}
X(s)
X(s)
H_1(s)
H_2(s)
Z(s)
¿Con notación de convolución?, ejemplos: enlace
V(s)
\mp
\displaystyle
\begin{array}{l}
Z(s)=\left(X(s)\mp Z(s)H_2(s) \right)H_1(s)\\
Z(s)\pm Z(s)H_2(s)H_1(s)= X(s)H_1(s)
\end{array}
\displaystyle
\begin{array}{l}
Z(s)=\frac{H_1(s)}{1\pm H_2(s)H_1(s)} X(s)
\end{array}
Nota
Los diagramas de bloque no son exclusivos para sistemas LTI su uso se extiende para la representación de flujo de información de los sistemas en general, aunque no puede hablar en concreto de una álgebra de bloques (sistemas).
Propiedades de los sistemas LTI continuos
\sum

x(t)
y(t)
Entrada trasladada produce salida trasladada (TI)
\sum

x(t+h)
y(t+h)
\sum

-\frac{1}{h}x(t+h)
-\frac{1}{h}y(t+h)
Entrada escalada produce salida escalada (L)
\sum

\frac{1}{h}x(t)
\displaystyle \lim_{h\to 0}\frac{y(t)-y(t+h)}{h}=\dot{y}(t)
Entrada escalada produce salida escalada (L)
\sum

\displaystyle \dot{x}(t)=\lim_{h\to 0}\frac{x(t)-x(t+h)}{h}
\frac{1}{h}y(t)
Suma de entradas produce suma de salidas (L)
En un sistema LTI continuo la respuesta a la derivada de una entrada conocida es la correspondiente derivada de la salida
Propiedades de los sistemas LTI continuos
\sum

x(t)
y(t)
\sum

x(t)(t_i-t_{i-1})
y(t)(t_i-t_{i-1})
Entrada escalada produce salida escalada (L)
Si repetimos el procedimiento para cada intervalo de la
\sum

\displaystyle \int_0^t{x}(\tau)d\tau=\lim_{n\to \infty}\sum_{i=1}^{n}x(t_i^*)\Delta t_i
partición, Suma de entradas produce suma de salidas (L)
En un sistema LTI continuo la respuesta a la integral de una entrada conocida es la correspondiente integral de la salida
Al evaluar en un punto que pertenezca a
\Delta t_i=t_i-t_{i-1}
\sum

x(t_i^*)\Delta t_i
y(t_i^*)\Delta t_i
Tomamos un intervalo [0, t]. Hacemos una partición de tal manera que
t_0=0,\ldots,t_n=t
\displaystyle \lim_{n \to \infty}\sum_{i=1}^{n}y(t_i^*)\Delta t_i=\int_0^t{y}(\tau)d\tau
Sistemas LTI continuos causales
\sum

x(t)
y(t)
Al evaluar en un tiempo a se quisiera que sea menor que , pero entonces si cada que se tendría causalidad
\displaystyle y(t)= x(t)*h(t)=\int_{-\infty}^{\infty}x(\tau)h(t-\tau)\,d\tau
\displaystyle y(t)=\int_{-\infty}^{\infty}x(\tau)h(t-\tau)\,d\tau=\int_{-\infty}^{t}x(\tau)h(t-\tau)\,d\tau+\int_{t}^{\infty}x(\tau)h(t-\tau)\,d\tau
\displaystyle y(t)=\int_{-\infty}^{t}x(\tau)h(t-\tau)\,d\tau
t
y
\tau
t
-\infty<\tau<\infty
h(t-\tau)=0
t<\tau
Por otro lado, con un cambio de variable, se tiene que la condición antes señalada equivale a cuando es decir, la respuesta al impulso es causal.
h(u)=0
u < 0
\displaystyle y(t)=\int_{-\infty}^{t}x(\tau)h(t-\tau)\,d\tau=\int_{0}^{\infty}x(t-u)h(u)\,du
Para un sistema LTI causal continuo con entrada en se tiene que la salida es:
t_0=0^-
\displaystyle y(t)=\int_{t_0}^{t}x(\tau)h(t-\tau)\,d\tau
\displaystyle y(t)=\int_{0^-}^{t}x(\tau)h(t-\tau)\,d\tau
Entonces, tenemos que:
Y en particular:
Si se quiere indicar que la entrada se manifiesta en el sistema en un tiempo determinado ,, es decir que para , entonces
t_0
x(\tau)=0
\tau < t_0
\displaystyle y(t)=\int_{-\infty}^{t}x(\tau)h(t-\tau)\,d\tau= \int_{-\infty}^{t_0}x(\tau)h(t-\tau)\,d\tau+\int_{t_0}^{t}x(\tau)h(t-\tau)\,d\tau
Sistemas diferenciales I
-
Respuesta a entrada cero
-
Respuesta a estado cero
Sistemas diferenciales
Llamamos sistemas diferenciales a aquellos cuya relación entre la entrada y la salida esta dada por una ecuación diferencial. Este formato también se conoce con el nombre modelo entrada-salida.
a_n\frac{d^n}{dt^n}y(t)+\ldots+a_1\frac{d}{dt}y(t)+a_0y(t)=b_m\frac{d^m}{dt^m}x(t)+\ldots+b_1\frac{d}{dt}x(t)+b_0x(t)
\displaystyle \sum_{i=0}^{n}a_i\frac{d^i}{dt^i}y(t)=\sum_{j=0}^{m}b_j\frac{d^j}{dt^j}x(t)
con
\displaystyle \frac{d^0}{dt^0}y(t)=y(t)\;\;\frac{d^0}{dt^0}x(t)=x(t)
x(t)
entrada
y(t)
salida
si se define
\displaystyle D^{k}=\frac{d^k}{dt^k},\;\;D^{0}=1
a_nD^ny(t)+\ldots+a_1Dy(t)+a_0y(t)=b_mD^mx(t)+\ldots+b_1Dx(t)+b_0x(t)
\displaystyle \sum_{i=0}^{n}a_iD^iy(t)=\sum_{j=0}^{m}b_jD^jx(t)
tenemos
Con la notación anterior se puede operar la ecuación como una multiplicación (parecido a la transformada de Laplace)
con
Q(D)\equiv a_nD^n+\ldots+a_1D+a_0
a_nD^ny(t)+\ldots+a_1Dy(t)+a_0y(t)=b_mD^mx(t)+\ldots+b_1Dx(t)+b_0x(t)
\left(a_nD^n+\ldots+a_1D+a_0\right)y(t)=\left(b_mD^m+\ldots+b_1D+b_0\right)x(t)
Q(D)y(t)=P(D)x(t)
P(D)\equiv b_mD^m+\ldots+b_1D+b_0
para resolver el problema directo en estos sistemas, se necesita conocer
y
y(t_0),\dot{y}(t_0),\ldots,\dot{y}^{(n-1)}(t_0)
x(t)
x(t_0),\dot{x}(t_0),\ldots,\dot{x}^{(n-1)}(t_0)
y(0^-),\dot{y}(0^-),\ldots,\dot{y}^{(n-1)}(0^-)
x(t)
x(0^-)=\dot{x}(0^-)=\dot{x}^{(n-1)}(0^-)=0
Resolveremos estos sistemas para un ejemplo específico y después generalizamos los resultados que se observan.
Si pensamos que la entrada es causal y que se tiene la entrada en el sistema para el tiempo igual a cero, entonces basta conocer la entrada y las condiciones iniciales de la salida
Este resultado se debe a que si una señal es causal su derivada evaluada a la izquierda del cero es cero. En general los coeficientes de la ecuación diferencial pueden ser dependientes del tiempo, pensamos por el momento que son constantes (posteriormente aclaramos esto).
Adicionalmente suponemos regiones de convergencia derechas (posteriormente aclaramos esto).
Sistemas diferenciales de primer orden: Respuesta a entrada cero
y(0^-)
x(t)=0
Pensemos en el sistema de primer orden dado por
Aplicamos transformada de Laplace
a_1\frac{d}{dt}y(t)+a_0y(t)=b_0x(t)
condición inicial
entrada causal
\displaystyle Y(s)={\frac{y(0^-)}{s+\frac{a_0}{a_1}}}=Y_{y_0}(s)
\displaystyle Y_{y_0}(s)={\frac{y(0^-)}{s+\frac{a_0}{a_1}}}
Respuesta a entrada cero: Esta presente si la entrada es cero
Respuesta a entrada cero: Depende de las condiciones iniciales del sistema y de los "modos" del sistema
\displaystyle
\begin{array}{rl}
y(t)=&y(0^-)e^{-\frac{a_0}{a_1}t}u(t)\\
=&y_{y_0}(t)
\end{array}
queremos conocer la respuesta (solución o salida) para
0\leq t
\displaystyle m_1(t)=e^{-\frac{a_0}{a_1}t}u(t)
Definimos a
como el modo del sistema
Sistemas diferenciales de primer orden: Respuesta al impulso
y(0^-)=0
x(t)=\delta(t)
Pensemos en el sistema de primer orden dado por
Aplicamos transformada de Laplace
a_1\frac{d}{dt}y(t)+a_0y(t)=b_0x(t)
condición inicial
entrada causal
\displaystyle Y(s)=\frac{b_0/a_1}{s+\frac{a_0}{a_1}}X(s)=\frac{b_0/a_1}{s+\frac{a_0}{a_1}}
Por lo regular cuando se encuentra la respuesta al impulso de un sistema se le suele denotar con la letra h, en este caso
\displaystyle y(t)=\frac{b_0}{a_1}e^{-\frac{a_0}{a_1}t}u(t)
\displaystyle h(t)=\frac{b_0}{a_1}e^{-\frac{a_0}{a_1}t}u(t)
queremos conocer la respuesta (solución o salida) para
0\leq t
Respuesta al impulso: Depende del "modo" del sistema
Nota
Es importante recordar la definición de transformada de Laplace unilateral derecha.
\displaystyle \mathscr{L}\lbrace f(t)\rbrace=\int_{0^-}^{\infty}f(t)e^{-st}d\tau
Esto permite que la transformada del impulso exista y sea igual a 1 y al mismo tiempo permite que en la transformadas de las derivadas aparezcan las condiciones iniciales y así resolver ciertos problemas de valor inicial (ecuaciones diferenciales con condiciones iniciales). En particular estas condiciones son las de la salida del sistema antes de que la entrada este presente, pues son en cero por la izquierda, "antes de conectar la entrada".
Sistemas diferenciales de primer orden: Respuesta a estado cero
y(0^-)=0
x(t)
Pensemos en el sistema de primer orden dado por
Aplicamos transformada de Laplace
a_1\frac{d}{dt}y(t)+a_0y(t)=b_0x(t)
condición inicial
entrada causal
\displaystyle Y(s)=\frac{b_0/a_1}{s+\frac{a_0}{a_1}}X(s)=Y_{x_0}(s)
\displaystyle Y_{x_0}(s)=\frac{b_0/a_1}{s+\frac{a_0}{a_1}}X(s)
Respuesta a estado cero: Esta presente si las condiciones iniciales son cero
\displaystyle
\begin{array}{rl}
y(t)=&x(t)*\frac{b_0}{a_1}e^{-\frac{a_0}{a_1}t}u(t)\\
=&x(t)*h(t)\\
=&\int_{0^-}^{t}x(\tau)\frac{b_0}{a_1}e^{-\frac{a_0}{a_1}(t-\tau)}d\tau\\
=&y_{x_0}(t)
\end{array}
Respuesta a estado cero: Convolución de la entrada con la respuesta al impulso del sistema
queremos conocer la respuesta (solución o salida) para
0\leq t
Sistemas diferenciales de primer orden: Respuesta total
y(0^-)
x(t)
Pensemos en el sistema de primer orden dado por
Aplicamos transformada de Laplace
a_1\frac{d}{dt}y(t)+a_0y(t)=b_0x(t)
condición inicial
entrada causal
\displaystyle Y(s)={\frac{y(0^-)}{s+\frac{a_0}{a_1}}}+\frac{b_0/a_1}{s+\frac{a_0}{a_1}}X(s)=Y_{y_0}(s)+Y_{x_0}(s)
\displaystyle Y_{y_0}(s)={\frac{y(0^-)}{s+\frac{a_0}{a_1}}}
\displaystyle Y_{x_0}(s)=\frac{b_0/a_1}{s+\frac{a_0}{a_1}}X(s)
Respuesta a entrada cero: Esta presente si la entrada es cero
Respuesta a estado cero: Esta presente si las condiciones iniciales son cero
queremos conocer la respuesta (solución o salida) para
0\leq t
Aplicamos transformada inversa
\displaystyle
\begin{array}{rl}
y(t)=&y(0^-)e^{-\frac{a_0}{a_1}t}u(t)+x(t)*\frac{b_0}{a_1}e^{-\frac{a_0}{a_1}t}u(t)\\
=&y(0^-)e^{-\frac{a_0}{a_1}t}u(t)+x(t)*h(t)\\
=&y(0^-)e^{-\frac{a_0}{a_1}t}u(t)+\int_{0^-}^{t}x(\tau)\frac{b_0}{a_1}e^{-\frac{a_0}{a_1}(t-\tau)}d\tau\\
=&y_{y_0}(t)+y_{x_0}(t)
\end{array}
\displaystyle y_{y_0}(t)=y(0^-)e^{-\frac{a_0}{a_1}t}u(t)
\displaystyle y_{x_0}(t)=x(t)*h(t)
Respuesta a entrada cero: Depende de las condiciones iniciales del sistema y de los "modos" del sistema
Respuesta a estado cero: Convolución de la entrada con la respuesta al impulso del sistema (la respuesta al impulso también depende de los "modos" del sistema).
La salida de todo sistema de primer orden diferencial (como lo hemos definido) tiene dos componentes, la componente de
RESPUESTA A ENTRADA CERO y la componente de RESPUESTA A ESTADO CERO
Nota.
La Respuesta a entrada cero y la Respuesta a estado cero son independientes una de la otra como se pudo observar en el procedimiento, es decir, el cálculo de una parte no interfiere en la otra y viceversa.
Esta descomposición es importante, pues permite encontrar la solución en términos de los efectos que produce la entrada y los efectos que producen las condiciones iniciales. Estas condiciones se pueden obtener del propio sistema y algunas manipulaciones del modelo. Esto último no siempre ocurre, pues cuando se tiene la Respuesta Natural (o solución homogénea) y la Respuesta Forzada (o solución particular), que veremos después, las condiciones iniciales no se pueden obtener del propio sistema.
\displaystyle
\begin{array}{rl}
y(t)=&y(0^-)e^{-\frac{a_0}{a_1}t}u(t)+x(t)*\frac{b_0}{a_1}e^{-\frac{a_0}{a_1}t}u(t)\\
=&y(0^-)e^{-\frac{a_0}{a_1}t}u(t)+x(t)*h(t)\\
=&y(0^-)e^{-\frac{a_0}{a_1}t}u(t)+\int_{0^-}^{t}x(\tau)\frac{b_0}{a_1}e^{-\frac{a_0}{a_1}(t-\tau)}d\tau\\
=&y_{y_0}(t)+y_{x_0}(t)
\end{array}
-
Causalidad
-
Memoria
-
Invariancia en tiempo
-
Linealidad
-
Causalidad
-
Memoria
-
Invariancia en tiempo
-
Linealidad
\displaystyle
\begin{array}{rl}
y(t)=&x(t)*\frac{b_0}{a_1}e^{-\frac{a_0}{a_1}t}u(t)\\
=&x(t)*h(t)\\
=&\int_{0^-}^{t}x(\tau)\frac{b_0}{a_1}e^{-\frac{a_0}{a_1}(t-\tau)}d\tau\\
=&y_{x_0}(t)
\end{array}
Un sistema de primer orden diferencial (como lo hemos definido) es LTI cuando las condiciones iniciales son cero, es decir, si el sistema esta en reposo.
Sistema de primer orden diferencial LTI
En un sistema de primer orden diferencial LTI (como lo hemos definido) la función de transferencia (transformada de Laplace de la respuesta al impulso, transformada de Laplace de la salida entre la transformada de la entrada) es:
X(s)
\displaystyle Y(s)=X(s)H(s)
H(s)

Y(s)
Pero sabemos que cuando un sistema es LTI
y(0^-)=0
x(t)=\delta(t)
a_1\frac{d}{dt}y(t)+a_0y(t)=b_0x(t)
a_1Dy(t)+a_0y(t)=b_0x(t)
\displaystyle \frac{Y(s)}{X(s)}=H(s)=\frac{b_0}{a_1s+a_0}=\frac{P(s)}{Q(s)}
Q(D)=a_1D+a_0
P(D)=b_0
\displaystyle Y(s)=\frac{b_0}{a_1s+a_0}X(s)
X(s)

Y(s)
\frac{b_0}{a_1s+a_0}
\displaystyle H(s)=\frac{P(s)}{Q(s)}
Sistemas diferenciales de orden n: Respuesta a entrada cero
x(t)=0
Aplicamos transformada de Laplace
condiciónes iniciales
entrada causal
queremos conocer la respuesta (solución o salida) para
0\leq t
a_nD^ny(t)+\ldots+a_1Dy(t)+a_0y(t)=b_mD^mx(t)+\ldots+b_1Dx(t)+b_0x(t)
y(0^-),\dot{y}(0^-),\ldots,\dot{y}^{(n-1)}(0^-)
a_nD^ny(t)+\ldots+a_1Dy(t)+a_0y(t)=0
\displaystyle a_ns^nY(s)+\ldots+a_1sY(s)+a_0Y(s)=\sum_{k=1}^{n}s^{n-k}y^{(k-1)}(0^-)+\ldots+sy(0^-)
\displaystyle Y(s)=\frac{\sum_{k=1}^{n}s^{n-k}y^{(0^-)}+\ldots+sy(0^-)}{a_ns^n+\ldots+a_1s+a_0}=\frac{R(s)}{Q(s)}
R(s) es un polinomio de grado menor que n y los coeficientes dependen de las condiciones iniciales.
\displaystyle Y(s)=\frac{R(s)}{Q(s)}=\frac{R(s)}{(s-p_1)\ldots(s-p_r)^{l_r}\ldots(s^2+2d_1s+c_1)\ldots (s^2+2d_is+c_i)^{q_i}}
\displaystyle =\frac{A_1}{(s-p_1)}+\ldots+\frac{A_{l_r}}{(s-p_r)^{l_r}}+\ldots+\frac{A_{d_1}s+B_{d_{1}}}{(s^2+2d_1s+c_1)}+\ldots +\frac{A_{d_i}s+B_{d_{i}}}{(s^2+2d_is+c_i)^{q_i}}
Dependiendo de la factorización, las n posibles funciones asociadas tendrán la forma
e^{p_1t}u(t)
\begin{array}{l}
e^{p_rt}u(t)\\
te^{p_rt}u(t)\\
\vdots\\
t^{l_r-1}e^{p_rt}u(t)
\end{array}
Las fracciones parciales dependen de Q(s) que se define como el polinomio característico.
\begin{array}{l}
e^{-d_1t}cos(\sqrt{c_1-d_1^2}\,t)u(t)\\
e^{-d_1t}sen(\sqrt{c_1-d_1^2}\,t)u(t)
\end{array}
\begin{array}{l}
e^{-d_it}cos(\sqrt{c_i-d_i^2}\,t)u(t)\\
e^{-d_it}sen(\sqrt{c_i-d_i^2}\,t)u(t)\\
te^{-d_it}cos(\sqrt{c_i-d_i^2}\,t)u(t)\\
te^{-d_it}sen(\sqrt{c_i-d_i^2}\,t)u(t)\\
\vdots\\
t^{q_i-1}e^{-d_it}cos(\sqrt{c_i-d_i^2}\,t)u(t)\\
t^{q_i-1}e^{-d_it}sen(\sqrt{c_i-d_i^2}\,t)u(t)\\
\end{array}
La respuesta a entrada cero para un sistema de orden n diferencial es:
\displaystyle y(t)=\sum_{i=1}^n K_im_i(t)=y_{y_0}(t)
Donde las funciones se conocen como los modos del sistemas
m_i(t)
Sistemas diferenciales de orden n: Respuesta al impulso
x(t)=\delta(t)
Aplicamos transformada de Laplace
condiciónes iniciales
entrada causal
queremos conocer la respuesta (solución o salida) para
0\leq t
a_nD^ny(t)+\ldots+a_1Dy(t)+a_0y(t)=b_mD^mx(t)+\ldots+b_1Dx(t)+b_0x(t)
y(0^-)=\dot{y}(0^-)=\ldots=\dot{y}^{(n-1)}(0^-)=0
\displaystyle a_ns^nY(s)+\ldots+a_1sY(s)+a_0Y(s)=b_ms^m+\ldots+b_1s+b_0
\displaystyle Y(s)=\frac{b_ms^m+\ldots+b_1s+b_0}{a_ns^n+\ldots+a_1s+a_0}=\frac{P(s)}{Q(s)}
a_nD^ny(t)+\ldots+a_1Dy(t)+a_0y(t)=b_mD^m\delta(t)+\ldots+b_1D\delta(t)+b_0\delta(t)
\displaystyle Y(s)=b^{'}{ }_{m-n}s^{m-n}+b^{'}{ }_{m-n-1}s^{m-n-1}+\ldots+b_1^{'}s+b_0^{'}+\frac{T(s)}{a_ns^n+\ldots+a_1s+a_0}
T(s) es un polinomio de grado menor que n y los coeficientes dependen de las a y de las b
Las fracciones parciales del segundo término dependen del polinomio característico y como hemos visto la transfromada inversa de estos elementos es especifica así
La respuesta al impulso para un sistema de orden n diferencial es:
Donde las funciones se conocen como los modos del sistema. Observemos que si entonces la salida solo es combinación lineal de modos. Si la salida dependerá de los modos del sistemas, de impulsos, y de derivadas de este.
\displaystyle y(t)=\sum_{i=1}^{m-n+1}b'{ }_{m-n+1-i}\delta^{(m-n+1-i)}(t)+\sum_{i=1}^n C_im_i(t)=h(t)
m_i(t)
m< n
n\leq m
Sistemas diferenciales de orden n: Respuesta a estado cero
Al aplicar transformada inversa de Lapalce
Aplicamos transformada de Laplace
entrada causal
queremos conocer la respuesta (solución o salida) para
0\leq t
a_nD^ny(t)+\ldots+a_1Dy(t)+a_0y(t)=b_mD^mx(t)+\ldots+b_1Dx(t)+b_0x(t)
y(0^-)=\dot{y}(0^-)=\ldots=\dot{y}^{(n-1)}(0^-)=0
\displaystyle a_ns^nY(s)+\ldots+a_1sY(s)+a_0Y(s)=b_ms^mX(s)+\ldots+b_1sX(s)+b_0X(s)
\displaystyle Y(s)=\frac{b_ms^m+\ldots+b_1s+b_0}{a_ns^n+\ldots+a_1s+a_0}X(s)=\frac{P(s)}{Q(s)}X(s)=H(s)X(s)
a_nD^ny(t)+\ldots+a_1Dy(t)+a_0y(t)=b_mD^mx(t)+\ldots+b_1Dx(t)+b_0x(t)
x(t)
La respuesta a estado cero para un sistema de orden n diferencial es:
La convolución de la entrada con la respuesta al impulso del sistema.
\displaystyle y(t)=x(t)*h(t)=y_{x_0}(t)
Sistemas diferenciales de orden n: Respuesta total
Aplicamos transformada de Laplace
entrada causal
queremos conocer la respuesta (solución o salida) para
0\leq t
a_nD^ny(t)+\ldots+a_1Dy(t)+a_0y(t)=b_mD^mx(t)+\ldots+b_1Dx(t)+b_0x(t)
y(0^-),\dot{y}(0^-),\ldots,\dot{y}^{(n-1)}(0^-)
\displaystyle \sum_{i=0}^n a_is^iY(s)=\sum_{k=1}^{n}s^{n-k}y^{(k-1)}(0^-)+\ldots+sy(0^-)+\sum_{i=0}^m b_is^iX(s)
a_nD^ny(t)+\ldots+a_1Dy(t)+a_0y(t)=b_mD^mx(t)+\ldots+b_1Dx(t)+b_0x(t)
x(t)
\displaystyle Y(s)=\frac{\sum_{k=1}^{n}s^{n-k}y^{(k-1)}(0^-)+\ldots+sy(0^-)}{Q(s)}+\frac{P(s)}{Q(s)}X(s)
\displaystyle Y(s)=\frac{R(s)}{Q(s)}+H(s)X(s)=Y_{y_0}(s)+Y_{x_0}(s)
Al aplicar transformada inversa de Laplace
Al aplicar transformada inversa de Lapalce
La respuesta total para un sistema de orden n diferencial es:
modos del sistema y
Una combinación lineal de los modos del sistema (donde las constantes dependen de las condiciones iniciales) más la convolución de la entrada con la respuesta al impulso del sistema.
\displaystyle
\begin{array}{l}
y(t)=y_{y_0}(t)+y_{x_0}(t)\\
\\
y(t)=\sum_{i=1}^n K_im_i(t)+x(t)*h(t)
\end{array}
\displaystyle h(t)=\sum_{i=1}^{m-n+1}b'{ }_{m-n+1-i}\delta^{(m-n+1-i)}(t)+\sum_{i=1}^n C_im_i(t)
m_i(t)
Estabilidad de un tipo de sistemas
-
BIBO-estabilidad
-
Lyapunov-estabilidad
Estabilidad BIBO (estabilidad externa)
Este tipo de estabilidad (existen varias definiciones) esta asociada a la respuesta a estado cero, la definición caracteriza el comportamiento del sistema en el siguiente sentido.
Un sistema es BIBO estable (Bounded-Input Bounded-Ouput), si para toda entrada acotada se produce una respuesta acotada (en caso contrario es BIBO-inestable) es decir:
\sum

\left|x(t)\right| \leq M_x,\;\;\forall\,0\leq t
\left|y(t)\right| \leq M_y,\;\;\forall\,0\leq t
Un sistema LTI diferencial causal con entrada en 0 es BIBO estable si y solo si la siguiente condición se satisface
\displaystyle \int_{0^-}^\infty\left|h(t)\right|\,d\tau \leq M_h
Un sistema LTI diferencial causal con entrada en 0 y función de transferencia H(s) propia, es BIBO estable si y solo si cada polo tiene parte real negativa.
Estabilidad en el sentido de Lyapunov (estabilidad interna)
Este tipo de estabilidad (existen varias definiciones) esta asociada a la respuesta a entrada cero, la definición caracteriza el comportamiento del sistema en el siguiente sentido.
La respuesta a entrada cero de un sistema LTI diferencial, es marginalmente estable o estable en el sentido de Lyapunov si cada condición inicial finita genera una respuesta acotada. Si adicionalmente la respuesta tiende a cero cuando el tiempo tiende a infinito diremos que la respuesta es asintoticamente estable. Cuando esto no suceda diremos que la respuesta asociada es inestable.
Esta definición se puede verificar con las siguientes condiciones
Un sistema LTI diferencial continuo es marginalmente estable, si y solo si algunas de las raíces del polinomio característico (polos de la función de transferencia) tienen parte real cero y no se repiten y las demás tienen parte real negativa.
Un sistema LTI diferencial continuo es asintoticamente estable si y solo si todas los raíces del polinomio característico tienen parte real negativa.
Un sistema LTI diferencial continuo es inestable si y solo si alguna raíz del polinomio característico tiene parte real positiva o alguna que tenga parte real cero se repite.
Observamos que:
BIBO - Estable
Asintoticamente - Estable
Pero no al revés
Sistema LTI continuo BIBO-estable
\sum

x(t)
y(t)=x(t)*h(t)
\sum

x(t)=ku(t)
\displaystyle
\begin{array}{l}
y(t)=\int_{0^-}^{t}kh(\tau)d\tau\\
=k\int_{0^-}^{t}h(\tau)d\tau
\end{array}
Para respuesta al impulso, entrada causal y sistema BIBO-estable
Observamos lo siguiente
\sum

\displaystyle ku(t)
\displaystyle y(t)=\left(\int_{0^-}^{t}h(\tau)d\tau\right)ku(t)
\displaystyle \lim_{t\to \infty}y(t)=H(0)ku(t)
Sistema LTI continuo BIBO-estable
\sum

x(t)
y(t)=x(t)*h(t)
\sum

x(t)=e^{\zeta t}u(t)
\displaystyle
\begin{array}{l}
y(t)=\int_{0^-}^{t}h(\tau)e^{\zeta(t-\tau)}d\tau\\
=e^{\zeta t}\int_{0^-}^{t}h(\tau)e^{-\zeta\tau}d\tau
\end{array}
Para respuesta al impulso y entrada causales y sistema BIBO-estable
Observamos lo siguiente
\sum

\displaystyle e^{\zeta t}u(t)
\displaystyle y(t)=\left(\int_{0^-}^{t}h(\tau)e^{-\zeta\tau}d\tau\right)e^{\zeta t}u(t)
\displaystyle \lim_{t\to \infty}y(t)=H(\zeta)e^{\zeta t}u(t)
Respuestas: Transitoria-Estacionaria-Frecuencia
-
Respuesta en estado estacionario
-
Respuesta transitoria
-
Respuesta en frecuencia
Sistema LTI continuo BIBO-estable
\sum

x(t)
y(t)=x(t)*h(t)
\sum

\begin{array}{l}
x(t)=cos(\omega t)u(t)=\\
\frac{1}{2}e^{j\omega t}u(t)+\frac{1}{2}e^{-j\omega t}u(t)
\end{array}
\begin{array}{l}
y(t)= \frac{1}{2}\left(\int_{0^-}^{t}h(\tau)e^{-j\omega\tau}d\tau\right)e^{j\omega t}u(t)\\
+ \frac{1}{2}\left(\int_{0^-}^{t}h(\tau)e^{-(-j\omega)\tau}d\tau\right)e^{-j\omega t}u(t)
\end{array}
Para respuesta al impulso y entrada causales y sistema BIBO-estable
Tomamos el límite cuando el tiempo tiende a infinito
\sum

\displaystyle cos(\omega t)u(t)
\displaystyle |H(j\omega)|cos\left(\omega t + \angle H(j\omega)\right)u(t)
\displaystyle \lim_{t\to \infty}y(t)=\frac{1}{2}H(j\omega)e^{j\omega t}u(t)+\frac{1}{2}H(-j\omega)e^{-j\omega t}u(t)=|H(j\omega)|cos\left(\omega t + \angle H(j\omega)\right)u(t)
En particular para este caso se suele llamar respuesta en estado estacionario (estado estable, steady-state) a cuando el sistema sea asintoticamente estable pues esto implicará que a la parte de la respuesta que satisfaga se le llamará respuesta transitoria en este caso
\displaystyle \lim_{t\to \infty}y(t)=y_{ss}(t)
\displaystyle \lim_{t\to \infty}y(t)=0
y_t(t)
y(t)=y_t(t)+y_{ss}(t)
Es importante decir varias cosas aquí, en primera la expresión se conoce como la respuesta en frecuencia del sistema, pues como se puede observar para un sistema asintoticamente estable, la respuesta en estado estacionario es un escalamiento y traslación de la entrada (coseno o seno) dependiente de la expresión
La respuesta en frecuencia se podría encontrar de dos maneras:
-
Calcular la función de transferencia del sistema y evaluar en
-
Encontrar la la transformada de Fourier de la respuesta al impulso del sistema
Por último muy importante: si se conjuntan el segundo punto con el desarrollo anterior "resulta natural" decir que los resultados de las transformaciones (sobre todo Fourier más que Laplace) están en el dominio de la frecuencia, aunque prefiero simplemente hacerlo notar como se ha dicho.
H(j\omega)
H(j\omega)
s=j\omega
Sistemas diferenciales de orden n: Respuesta a estado cero
Al aplicar transformada inversa de Fourier
Aplicamos transformada de Fourier
entrada causal
queremos conocer la respuesta (solución o salida) para
0\leq t
a_nD^ny(t)+\ldots+a_1Dy(t)+a_0y(t)=b_mD^mx(t)+\ldots+b_1Dx(t)+b_0x(t)
y(0^-)=\dot{y}(0^-)=\ldots=\dot{y}^{(n-1)}(0^-)=0
\displaystyle a_n(j\omega)^nY(j\omega)+\ldots+a_1(j\omega)Y(j\omega)+a_0Y(j\omega)=b_m(j\omega)^mX(j\omega)+\ldots+b_1(j\omega)X(j\omega)+b_0X(s)
\displaystyle Y(j\omega)=\frac{b_m(j\omega)^m+\ldots+b_1(j\omega)+b_0}{a_n(j\omega)^n+\ldots+a_1(j\omega)+a_0}X(j\omega)=\frac{P(j\omega)}{Q(j\omega)}X(j\omega)=H(j\omega)X(j\omega)
a_nD^ny(t)+\ldots+a_1Dy(t)+a_0y(t)=b_mD^mx(t)+\ldots+b_1Dx(t)+b_0x(t)
x(t)
La respuesta a estado cero para un sistema de orden n diferencial es:
La convolución de la entrada con la respuesta al impulso del sistema.
\displaystyle y(t)=x(t)*h(t)=y_{x_0}(t)
Es decir si queremos encontrar la respuesta de un sistema diferencial mediante la transformada de Fourier, solo se pueden encontrar la respuesta a estado cero, es decir cuando el sistema esta en reposo. Y como se ha dicho cuando queremos encontrar la respuesta estacionaria para un sistema BIBO-estable
Sistemas diferenciales II
-
Respuesta natural (solución homogénea)
-
Respuesta forzada (solución particular)
-
Condiciones iniciales y
-
Soluciones numéricas
0^-
0^+
Sistemas diferenciales
Llamamos sistemas diferenciales a aquellos cuya relación entre la entrada y la salida esta dada por una ecuación diferencial. Este formato también se conoce con el nombre modelo entrada-salida.
a_n\frac{d^n}{dt^n}y(t)+\ldots+a_1\frac{d}{dt}y(t)+a_0y(t)=b_m\frac{d^m}{dt^m}x(t)+\ldots+b_1\frac{d}{dt}x(t)+b_0x(t)
\displaystyle \sum_{i=0}^{n}a_i\frac{d^i}{dt^i}y(t)=\sum_{j=0}^{m}b_j\frac{d^j}{dt^j}x(t)
con
\displaystyle \frac{d^0}{dt^0}y(t)=y(t)\;\;\frac{d^0}{dt^0}x(t)=x(t)
x(t)
entrada
y(t)
salida
si se define
\displaystyle D^{k}=\frac{d^k}{dt^k},\;\;D^{0}=1
a_nD^ny(t)+\ldots+a_1Dy(t)+a_0y(t)=b_mD^mx(t)+\ldots+b_1Dx(t)+b_0x(t)
\displaystyle \sum_{i=0}^{n}a_iD^iy(t)=\sum_{j=0}^{m}b_jD^jx(t)
tenemos
Q(D)\equiv a_nD^n+\ldots+a_1D+a_0
a_nD^ny(t)+\ldots+a_1Dy(t)+a_0y(t)=b_mD^mx(t)+\ldots+b_1Dx(t)+b_0x(t)
\left(a_nD^n+\ldots+a_1D+a_0\right)y(t)=\left(b_mD^m+\ldots+b_1D+b_0\right)x(t)
Q(D)y(t)=P(D)x(t)
P(D)\equiv b_mD^m+\ldots+b_1D+b_0
para resolver el problema directo en estos sistemas, se necesita conocer
y
y(t_0),\dot{y}(t_0),\ldots,\dot{y}^{(n-1)}(t_0)
x(t)
x(t_0),\dot{x}(t_0),\ldots,\dot{x}^{(n-1)}(t_0)
y(0^+),\dot{y}(0^+),\ldots,\dot{y}^{(n-1)}(0^+)
x(t)
Si pensamos que la entrada es causal y que se tiene la entrada en el sistema para el tiempo igual a cero, entonces basta conocer la entrada y las condiciones iniciales de la salida
Resolveremos estos sistemas para un ejemplo específico y después generalizamos los resultados que se observan.
En general los coeficientes de la ecuación diferencial pueden ser dependientes del tiempo, pensamos por el momento que son constantes (posteriormente aclaramos esto).
Las condiciones iniciales pueden justificarse de diferentes maneras, la más clara en el sentido operativo: son las que se necesitan de acuerdo a la metodología de solución.
Sistemas diferenciales de primer orden:
Respuesta natural (solución homogénea)
Pensemos en el sistema de primer orden dado por
a_1\frac{d}{dt}y(t)+a_0y(t)=0
Pensemos que la solución tiene la estructura en caso de ser solución, debería satisfacer la ecuación diferencial, entonces al sustituir
\displaystyle y_{N}(t)=y_{h}(t)=Ce^{-\frac{a_0}{a_1}t}
Respuesta natural: Esta presente independientemente si hay entrada o no, depende de las condiciones iniciales y de los modos del sistema
queremos conocer la respuesta (solución o salida) para
0\leq t
\displaystyle m_1(t)=e^{-\frac{a_0}{a_1}t}
Definimos a
como el modo del sistema
\displaystyle
\begin{array}{l}
a_1\frac{d}{dt}e^{\lambda t}+a_0e^{\lambda t}=0\\
\\
e^{\lambda t}\left(a_1\lambda+a_0\right)=0\\
\\
a_1\lambda+a_0=0\\
\\
Q(\lambda)=0
\end{array}
e^{\lambda t}
\displaystyle Q(\lambda)=0
Ecuación característica
Se Observa que
\displaystyle
a_1\frac{d}{dt}y_N(t)+a_0 y_N(t)=0
Sistemas diferenciales de primer orden:
Respuesta forzada (solución particular)
Pensemos en el sistema de primer orden dado por
a_1\frac{d}{dt}y(t)+a_0y(t)=b_0x(t)
queremos conocer la respuesta (solución o salida) para
0\leq t
Pensemos que la solución tiene una determinada estructura dependendiendo quien es la entrada, es decir:
\displaystyle
\begin{array}{|r|l|l|}
\#&\text{Entrada}&\text{Respuesta forzada}\\
&&\\
1.&e^{\zeta t},\;\zeta\neq\lambda_i&\beta e^{\zeta t}\\
&\\
2.&e^{\zeta t},\;\zeta=\lambda_i&\beta te^{\zeta t}\\
&\\
3.&k&\beta\\
&\\
4.&cos(\omega t+\theta)&\beta cos(\omega t+\phi)=\beta_1 cos(\omega t)+\beta_2 sen(\omega t)\\
\end{array}
Basta ver que para cada tipo de entrada propuesta la solución particular depende del coeficiente indeterminado. En general la respuesta forzada se propone de acuerdo a la estructura del operador diferencial que lo cancele
Pensemos que en nuestro ejemplo la entrada es del tipo 1, entonces
\displaystyle
\begin{array}{l}
a_1\beta\frac{d}{dt}e^{\zeta t}+a_0\beta e^{\zeta t}=b_0 e^{\zeta t}\\
\\
\beta e^{\zeta t}\left(a_1\zeta+a_0\right)=b_0 e^{\zeta t}\\
\\
\beta=\frac{b_0}{a_1\zeta+a_0}\\
\\
\beta=H(\zeta)
\end{array}
\beta e^{\zeta t}
\displaystyle y_{F}(t)=H(\zeta)e^{\zeta t}
Respuesta Forzada: Esta respuesta depende de la entrada.
Se Observa que
\displaystyle
a_1\frac{d}{dt}y_F(t)+a_0 y_F(t)=b_0 x(t)
En particular las funciones exponenciales son funciones propias, es decir, el sistema simplemente las escala, el escalamiento es la función de transferencia evaluada en el coeficiente de la exponencial.
Sistemas diferenciales de primer orden
Respuesta total
y(0^+)
x(t)
Pensemos en el sistema de primer orden dado por
Observemos lo siguiente:
a_1\frac{d}{dt}y(t)+a_0y(t)=b_0x(t)
entrada causal
\displaystyle y_{T}(t)=y_{N}(t)+y_{F}(t)
Respuesta total: Es la suma de la respuesta natural más la respuesta forzada
queremos conocer la respuesta (solución o salida) para
0\leq t
condición inicial
\displaystyle
\begin{array}{l}
a_1\frac{d}{dt}\left(y_N(t)+y_F(t)\right)+a_0\left(y_N(t)+y_F(t)\right)=\\
\\
a_1\frac{d}{dt}y_N(t)+a_0y_N(t)+a_1\frac{d}{dt}y_F(t)+a_0y_F(t)=\\
\\
0+b_0 x(t)=b_0x(t)\\
\\
\text{Definimos } y_T(t)=y_N(t)+y_F(t)
\end{array}
En nuestro ejemplo:
y_T(t)=Ce^{-\frac{a_0}{a_1}t}+H(\zeta)e^{\zeta t}
En este momento se encuentra a C
Sistemas diferenciales de orden n:
Respuesta total
x(t)
Escribimos el sistema homogeneo asociado
entrada causal
queremos conocer la respuesta (solución o salida) para
0\leq t
a_nD^ny(t)+\ldots+a_1Dy(t)+a_0y(t)=b_mD^mx(t)+\ldots+b_1Dx(t)+b_0x(t)
y(0^+),\dot{y}(0^+),\ldots,\dot{y}^{(n-1)}(0^+)
a_nD^ny(t)+\ldots+a_1Dy(t)+a_0y(t)=0
\displaystyle Q(s)=a_ns^n+\ldots+a_1s+a_0=0
Pensemos que la solución tiene la estructura en caso de ser solución, debería satisfacer la ecuación diferencial, entonces al sustituir tenemos la ecuación caracteristica
e^{\lambda t}
Paso\; 1.
condiciones iniciales
Paso\; 1.
Dependiendo de la forma de las raíces del polinomio característico (raíces características o valores propios del sistema) se tendrá que los n posibles modos del sistema serán
e^{pt}u(t)
\begin{array}{l}
e^{pt}u(t)\\
te^{pt}u(t)\\
\vdots\\
t^{r-1}e^{pt}u(t)
\end{array}
\begin{array}{l}
e^{\mathbb{R}e(p)t}cos(\mathbb{I}m(p)\,t)u(t)\\
e^{\mathbb{R}e(p)t}sen(\mathbb{I}m(p)\,t)u(t)
\end{array}
\begin{array}{l}
e^{\mathbb{R}e(p)t}cos(\mathbb{I}m(p)\,t)u(t)\\
e^{\mathbb{R}e(p)t}sen(\mathbb{I}m(p)\,t)u(t)\\
te^{\mathbb{R}e(p)t}cos(\mathbb{I}m(p)\,t)u(t)\\
te^{\mathbb{R}e(p)t}sen(\mathbb{I}m(p)\,t)u(t)\\
\vdots\\
t^{r-1}e^{\mathbb{R}e(p)t}cos(\mathbb{I}m(p)\,t)u(t)\\
t^{r-1}e^{\mathbb{R}e(p)t}sen(\mathbb{I}m(p)\,t)u(t)\\
\end{array}
Raíz real simple
Raíz real con repetición
Raíz compleja simple
Raíz compleja con repetición
La respuesta natural (solución homogénea) para un sistema de orden n diferencial es:
\displaystyle y_N(t)=\sum_{i=1}^n C_im_i(t)=y_h(t)
Se propone a la respuesta fozada (o solución particular) de acuerdo a según la tabla que se ha listado (en general un operador que cancele a la entrada). Se sustituye en ambos lados de la ecuación diferecial y se encuentra el coeficiente indeterminado
y_F(t)
Paso\; 2.
x(t)
a_nD^ny_p(t)+\ldots+a_1Dy_p(t)+a_0y_p(t)=b_mD^mx(t)+\ldots+b_1Dx(t)+b_0x(t)
La respuesta total es la suma de la respuesta natural (solución homogénea) más la respuesta forzada (solución particular) para un sistema de orden n diferencial es:
\displaystyle y_T(t)=y_N(t)+y_F(t)=\sum_{i=1}^n C_im_i(t)+y_F(t)=y_h(t)+y_p(t)
Se sustituyen las condiciones iniciales en la solución total para encontrar las constantes
Paso\; 3.
\displaystyle y_T(t)=\sum_{i=1}^n C_im_i(t)+y_F(t)
Condiciones Iniciales
0^-
0^+
a_2D^2y(t)+a_1Dy(t)+a_0y(t)=b_2D^2x(t)+b_1Dx(t)+b_0x(t)
Dependiendo de la metodología de solución se necesitarán las condiciones iniciales antes de "conectar" la entrada al sistema (transformada de Laplace), o inmediatamente después de "conectar" la entrada al sistema (solución homogénea y particular).
\displaystyle y(0^+)=y(0^-)+\frac{b_2}{a_2}\left(x(0^+)-x(0^-)\right)
\displaystyle \dot y(0^+)=\dot y(0^-)+\frac{b_2}{a_2}\left(\dot x(0^+)-\dot x(0^-)\right)+\frac{a_2b_1-a_1b_2}{(a_2)^2}\left( x(0^+)- x(0^-)\right)
Métodos Numéricos para ecuaciones diferenciales
h=0.3; % Elegimos el tamaño del paso
t(1)=0; % Tiempo inicial
tf=12; % Tiempo final
y(1)=10; % Condición inicial
puntos=floor((tf-t(1))/h)+1; % Puntos de la tabulación
for i=2:puntos
k1=-0.25*y(i-1)+1; %calculamos la derivada
y(i)=y(i-1)+k1*h; %calculamos el nuevo punto
t(i)=t(i-1)+h; %calculamos el nuevo tiempo
end
plot(t,y);
grid on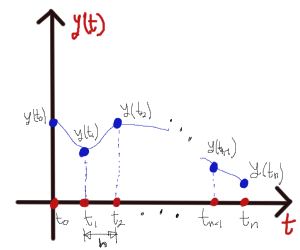
\displaystyle
\begin{array}{l}
\dot{y}(t)=f(y(t),t),\;y(t_0)\\
\\
\lim_{h\to 0}\frac{y(t+h)-y(t)}{h}=f(y(t),t)\\
\\
\frac{y(t+h)-y(t)}{h}\approx f(y(t),t)\\
\\
y(t+h)\approx y(t)+f(y(t),t)h\\
\\
y(t_{n+1})\approx y(t_{n})+f(y(t_n),t_n)h
\end{array}
Método de Euler. Método numérico de paso fijo para resolver ecuaciones diferenciales ordinarias de primer orden (no es el "mejor"). Existen diferentes métodos, dependiendo de la complejidad del problema.
\frac{d}{dt}y(t)+0.25y(t)=x(t)
Bibliografía
[1] Cellier, F.E . (1991), Continuous System Modeling, Springer-Verlag, NewYork.
[2] Dennis Freeman. 6.003 Signals and Systems. Fall 2011. Massachusetts Institute of Technology: MIT OpenCourseWare, https://ocw.mit.edu. License: Creative Commons BY-NC-SA.
Control
By ra_fa
Control
Introducción a sistemas, conceptos y definiciones básicas, sistemas LTI en tiempo continuo, sistemas LTI en tiempo discreto, sistemas diferenciales, sistemas en diferencias.
- 386



