Нейросети
Нейросети

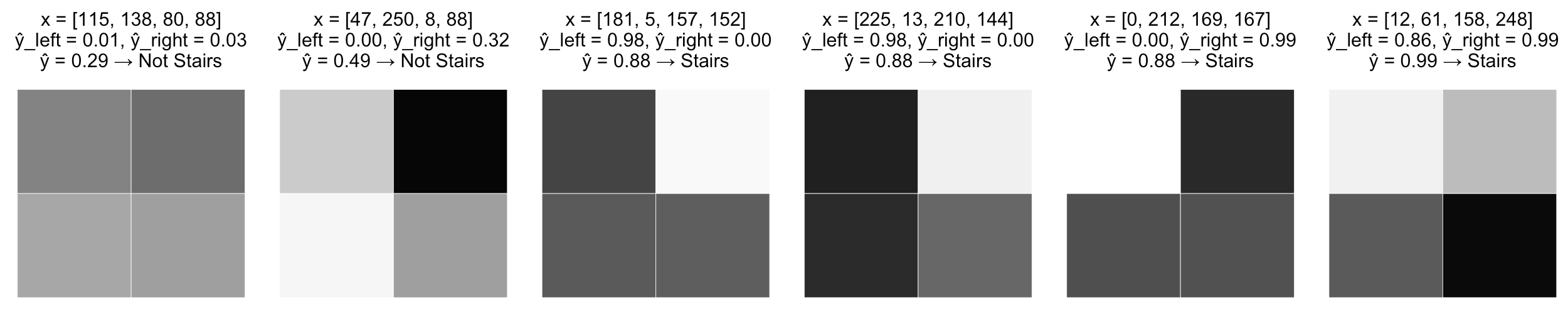
Рассмотрим задачу классификации изображений на два класса: "лестница" и "не лестница"
Нейросети

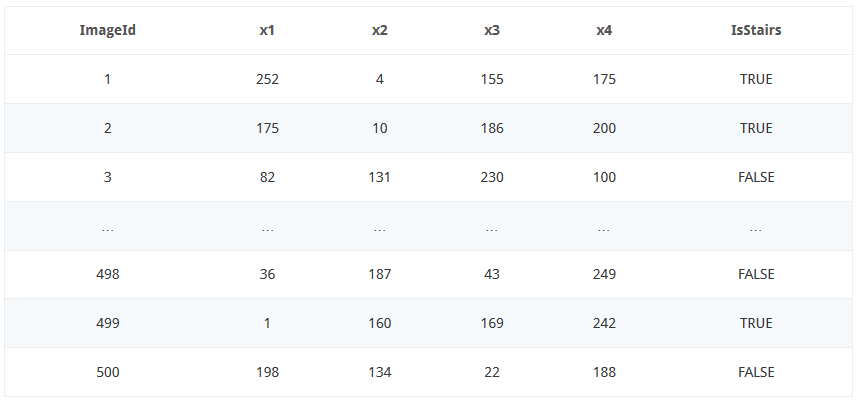
Опишем каждое изображение четырьмя признаками - интенсивностью черного цвета в каждом из пикселей
Перцептрон

Перцептрон
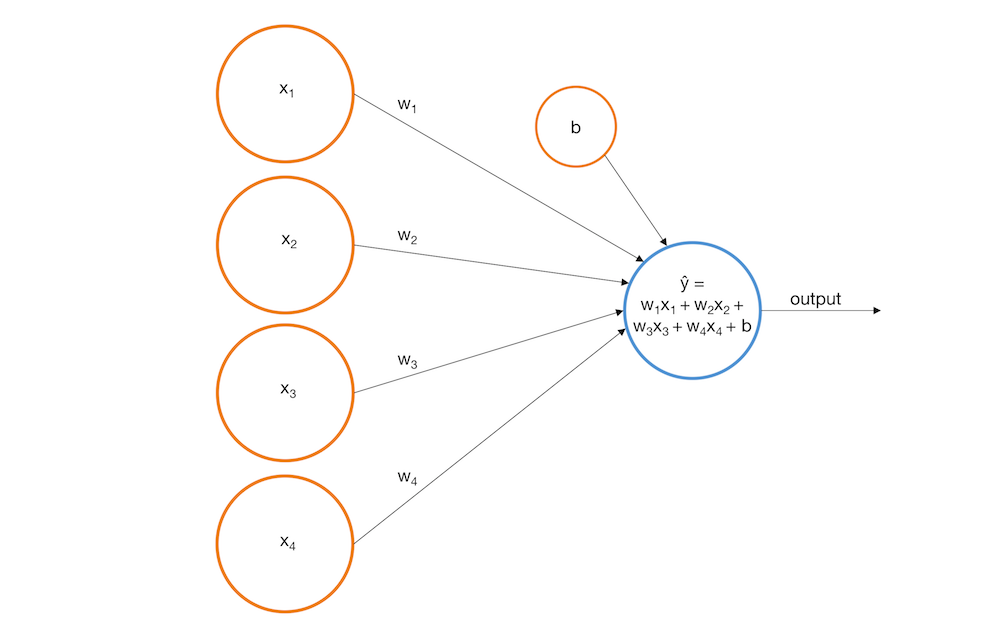
Перцептрон
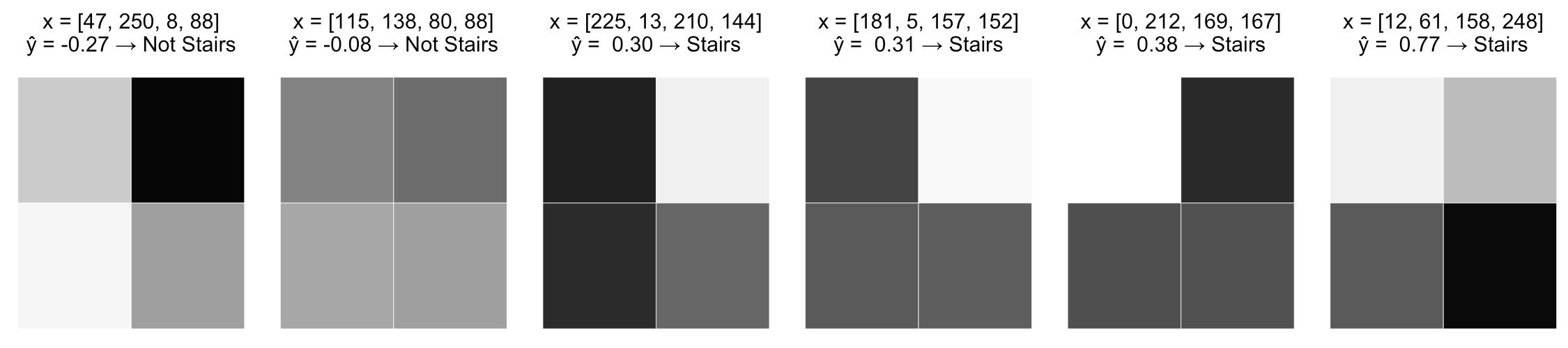
- нет вероятностной интерпретации: \(a(x) \not\subset [0, 1] \)
- модель не может ухватить нелинейные зависимости целевой переменной от признаков
(выглядит знакомо, не правда ли?)
Перцептрон
- модель не может ухватить нелинейные зависимости целевой переменной от признаков
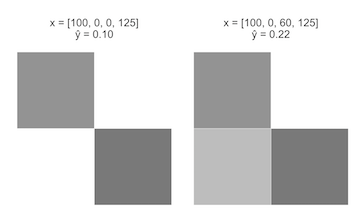
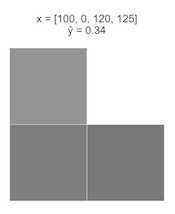
Переход к вероятностной интерпретации модели
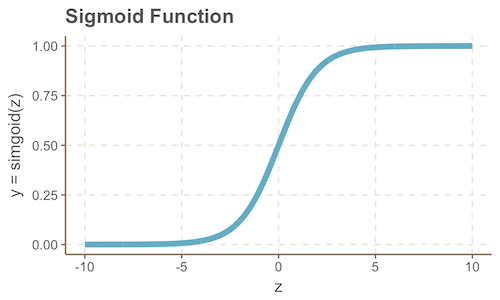
Переход к вероятностной интерпретации модели
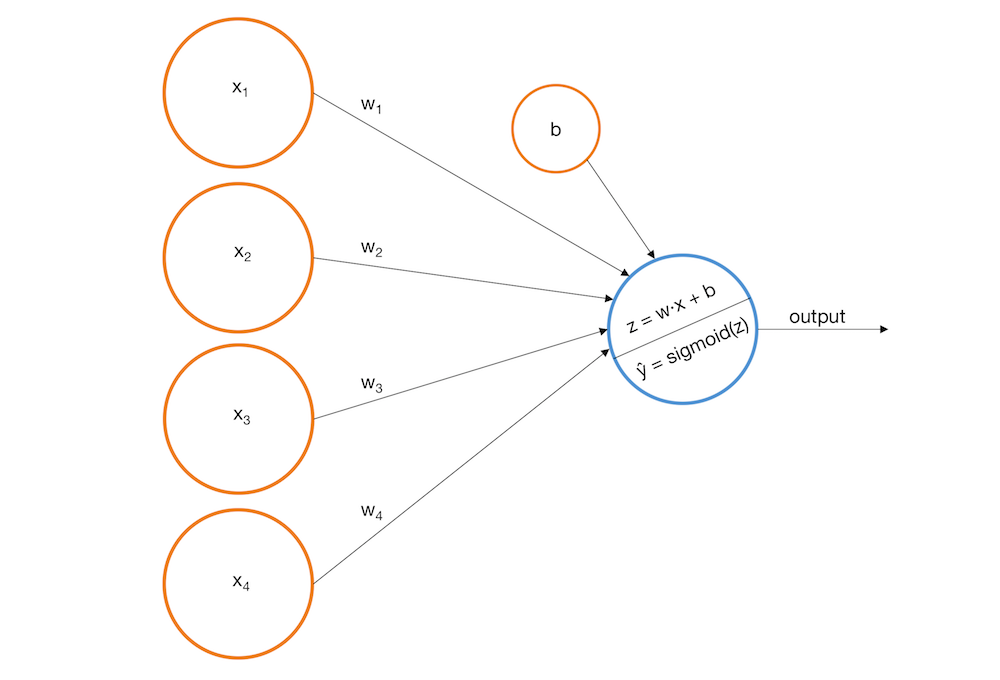
Переход к вероятностной интерпретации модели


Да это же логистическая регрессия!

Переход к вероятностной интерпретации модели
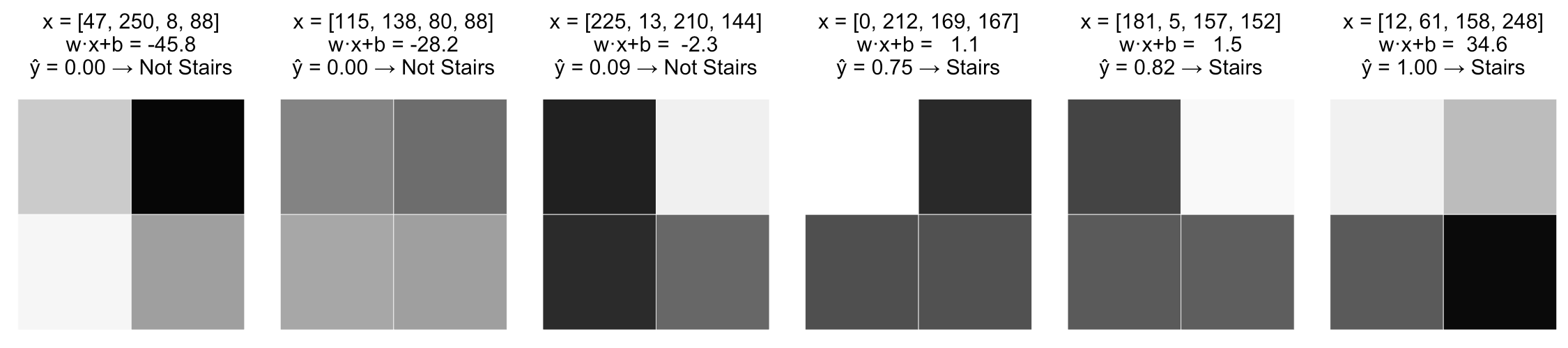
Переход к вероятностной интерпретации модели
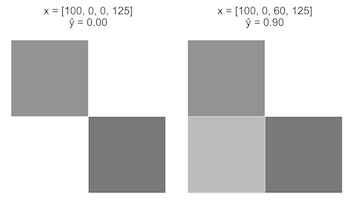

- теперь различия картинок трактуются более адекватно
Многослойные нейросети
Недостатки полученной модели
- \(\widehat y\) монотонно зависит от каждой переменной
- не учитывается взаимодействие переменных
Добавим слои
- построим две модели: для "левых" и "правых" лестниц
- будем давать положительный ответ, если оба классификатора дают высокие значения вероятности
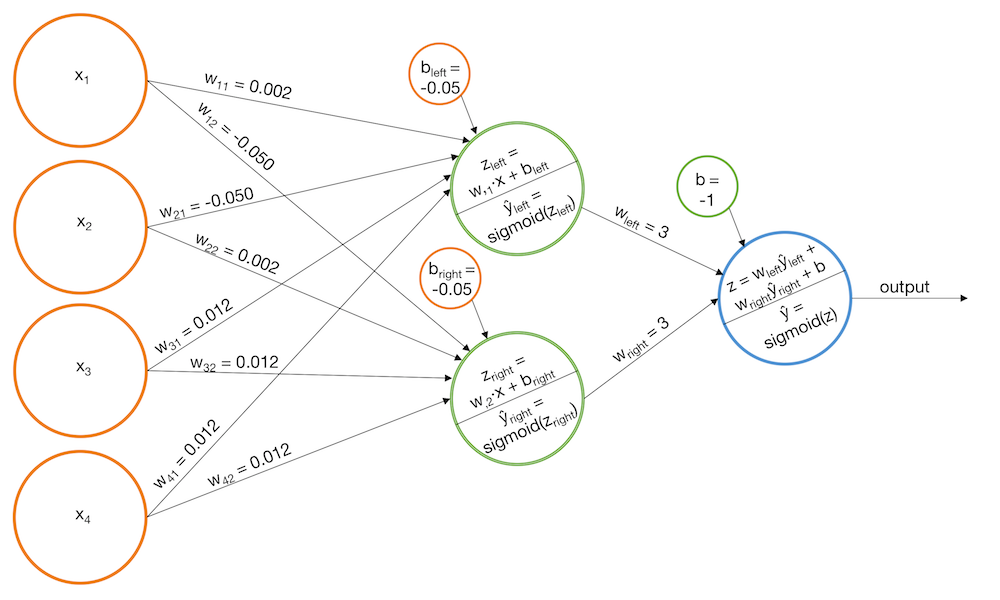
Добавим слои
- построим две модели: для "левых" и "правых" лестниц
- будем давать положительный ответ, если оба классификатора дают высокие значения вероятности
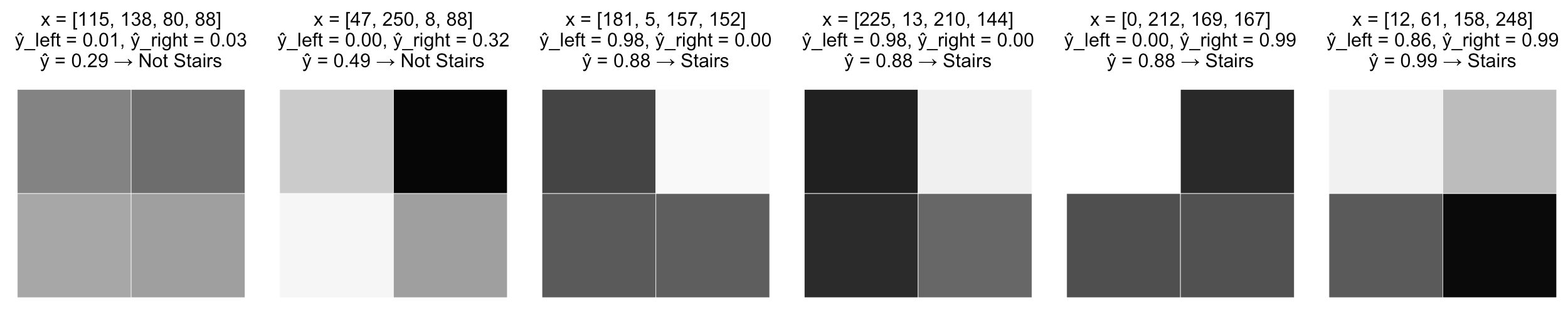
Другой вариант новых слоев
- построим модель, срабатывающую на темный нижний ряд
- модель, когда верхний левый пиксель темный, правый верхний - светлый и модель, когда верхний правый пиксель темный, верхний левый светлый
- финальная модель срабатывает тогда, когда 1 и 2 значения велики либо когда 1 и 3 значения велики
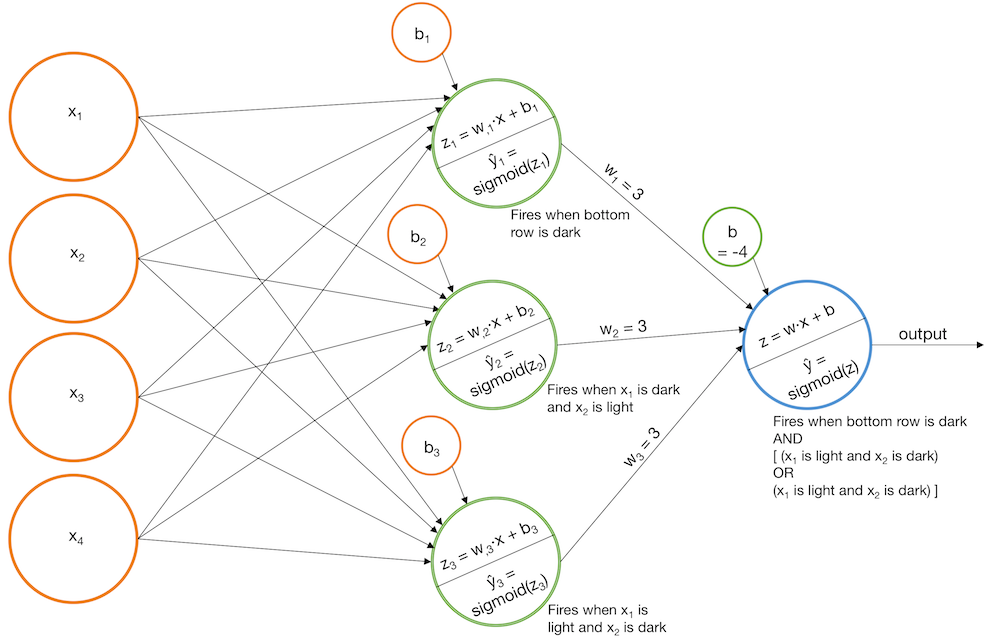
Другой вариант новых слоев
- построим модель, срабатывающую на темный нижний ряд
- модель, когда верхний левый пиксель темный, правый верхний - светлый и модель, когда верхний правый пиксель темный, верхний левый светлый
- финальная модель срабатывает тогда, когда 1 и 2 значения велики либо когда 1 и 3 значения велики
Нейронная реализация логических функций
\(x^1 \land x^2 = [x^1 + x^2 - \frac{3}{2} > 0]\)
\(x^1 \vee x^2 = [x^1 + x^2 - \frac{1}{2} > 0]\)
\(\neg x^1 = [-x^1 + \frac{1}{2} > 0]\)

Нейронная реализация логических функций
\(x^1 \oplus x^2 = [x^1 + x^2 - 2 x^1 x^2 - \frac{1}{2} < 0\)]
\(x^1 \oplus x^2 = [(x^1 \vee x^2) - (x^1 \land x^2) - \frac{1}{2} > 0]\)

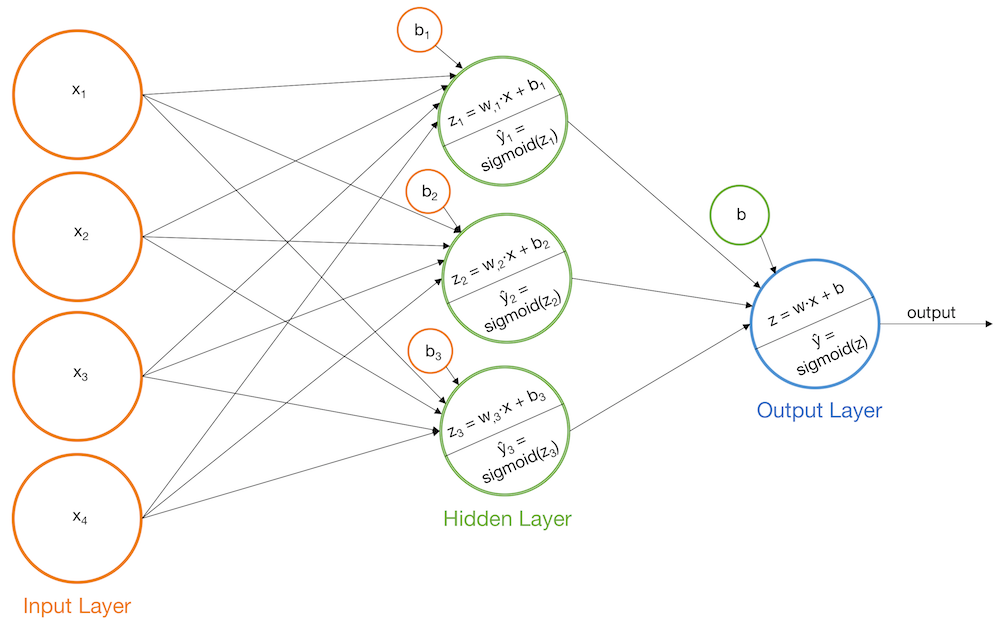
Термины в нейросетях
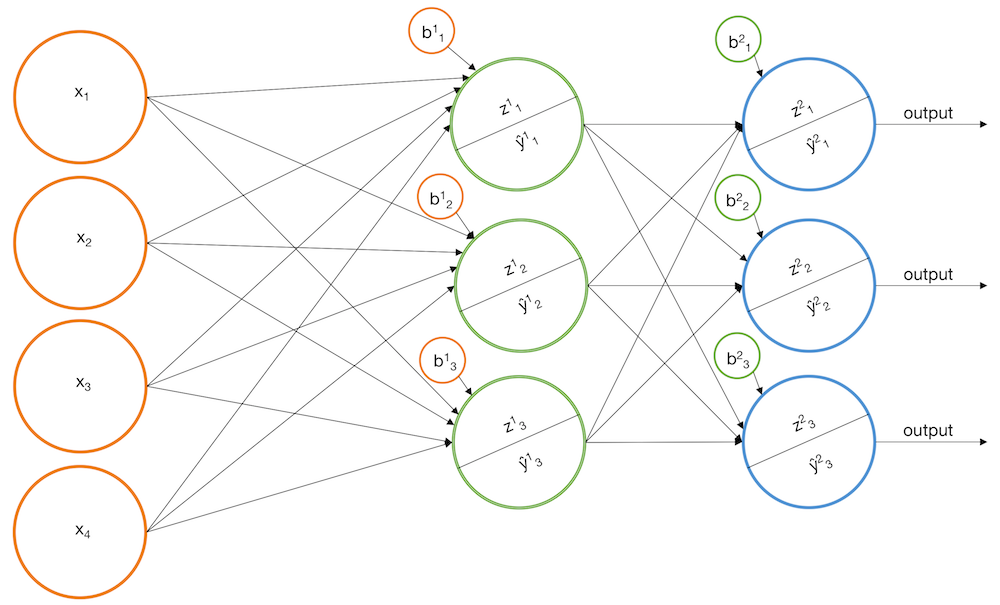
Обобщение на несколько классов
Функции активации
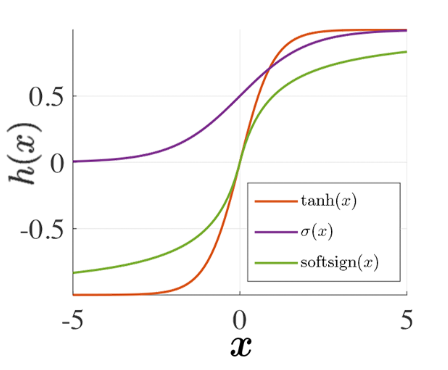
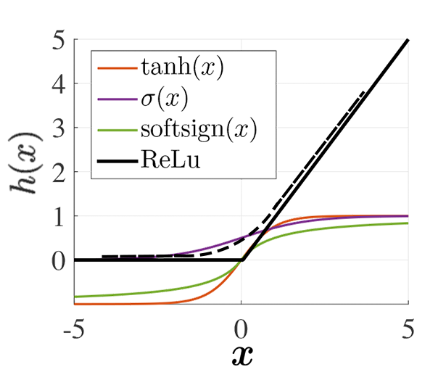
- непрерывно монотонные, лучше - дифференцируемые
Настройка многослойных нейросетей
Комбинация однослойных сетей
Однослойная сеть:
\(a(\vec x, \vec w) = \sigma(\vec w \vec x) = \sigma(\sum\limits_{j=1}^d w_j^{(1)} x_j + w_0^{(1)} ) \)
Двуслойная сеть:
\( a(\vec x, \vec w) = \sigma^{(2)} (\sum\limits_{j=1}^D w_i^{(2)} \sigma^{(1)} (\sum\limits_{j=1}^d w_{ji}^{(1)} x_j + w_{0i}^{(1)} ) + w_0^{(2)} ) \)
Соединенный вектор параметров:
\( \vec w = \{w_i^{(2)}, w_{ij}^{(1)}, w_{i0}^{(1)}, w_0^{(2)} \} \)
Задача оптимизации:
\(\vec w^{*} = \arg \min\limits_{\vec w} Q(\vec w) \)
Разделяющая поверхность
уже необязательно линейная
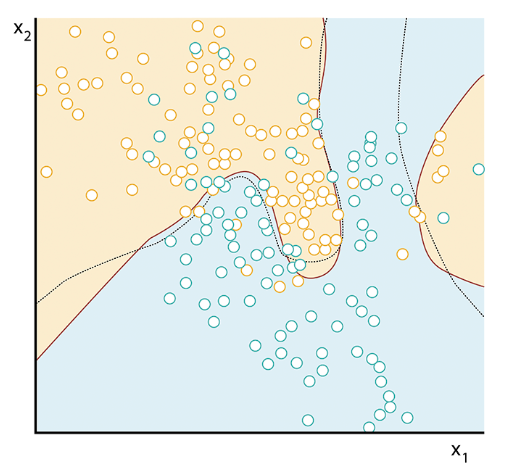
Теорема Колмогорова
Каждая непрерывная функция \(a(x)\), заданная на единичном кубе d-мерного пространства, представима в виде:
где \(x = [x_1, ..., x_d]^T\), функции \(\sigma_i(\dot), f_{ij}(\dot) \) непрерывны, причем \(f_{ij}\) не зависят от выбора \(a\)
Универсальная теорема аппроксимации (Хорника)
Искусственная нейросеть прямой связи с одним скрытым слоем может аппроксимировать любую непрерывную функцию многих переменных с любой точностью. Условиями для этого являются достаточное количество нейронов скрытого слоя и удачный подбор весов модели.
Причина частого выбора глубоких архитектур нейронных сетей вместо сетей с одним скрытым слоем заключается в том, что при процедуре подбора они обычно сходятся к решению быстрее.
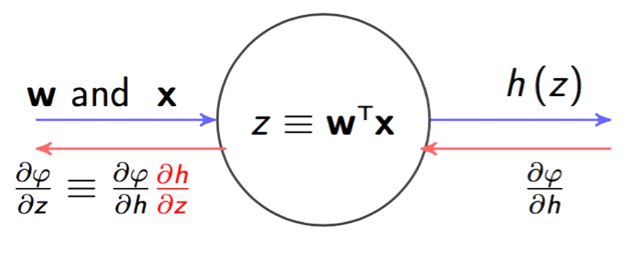
Метод обратного распространения ошибки
Имеем размеченные данные, выбрали дифференцируемую функцию потерь и архитектуру сети
- инициализируем сеть со случайными параметрами
- считаем предсказания на обучающей выборке, получаем первоначальный \(L(\widehat Y, Y)\)
- вычисляем \(\nabla L\) с учетом каждого веса в сети
- шаг в сторону антиградиента

Регуляризация нейросетей
Как и у других линейных методов:
- не снижает число параметров, не упрощает структуру сети
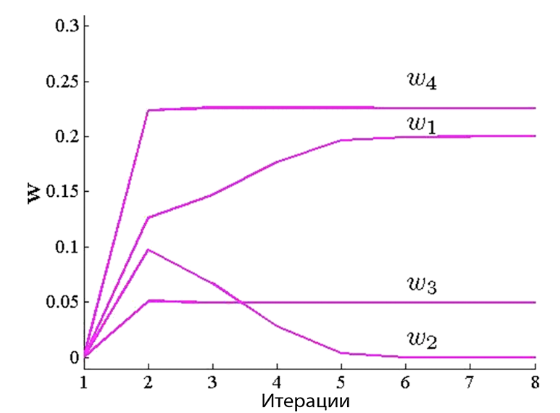
- при увеличении \(\tau\) параметры перестают изменяться
Прореживание нейросетей
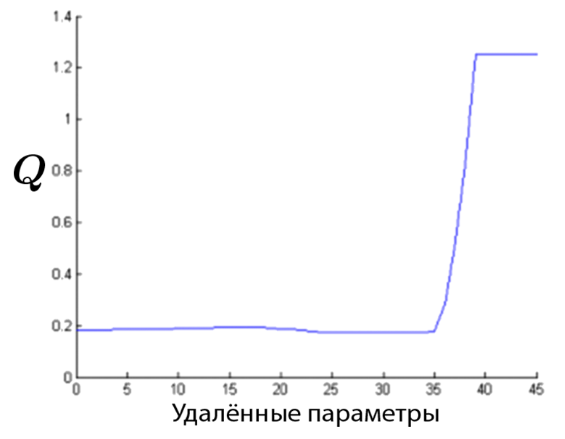
Удаляем параметр, если:
- его значение близко к 0
- его значение сильно изменяется при изменении выборки
- его удаление незначительно влияет на значение функционала ошибки
Dropout
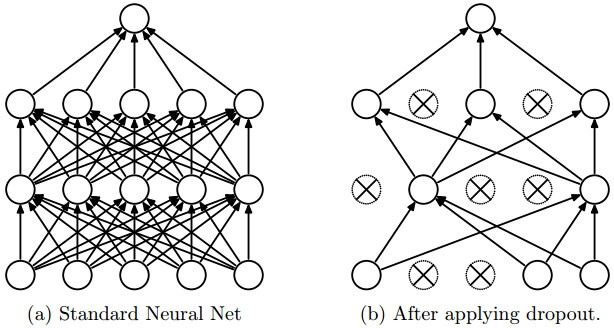
Стабилизация параметров нейросетей
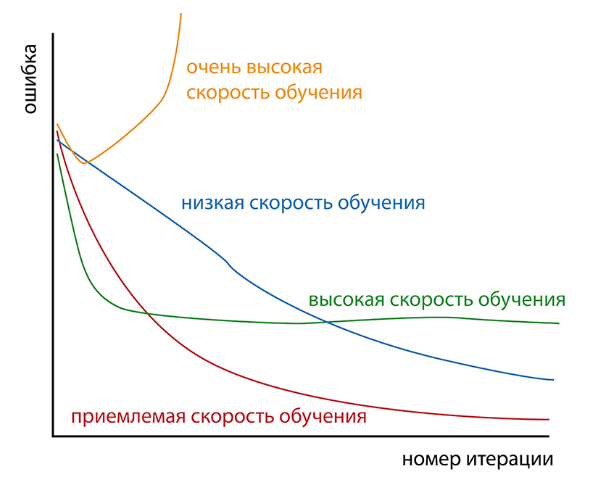
Скорость обучения нейросетей
Архитектуры нейросетей
Сверточные нейросети

Свертка изображения (convolution)
Слой макспуллинга
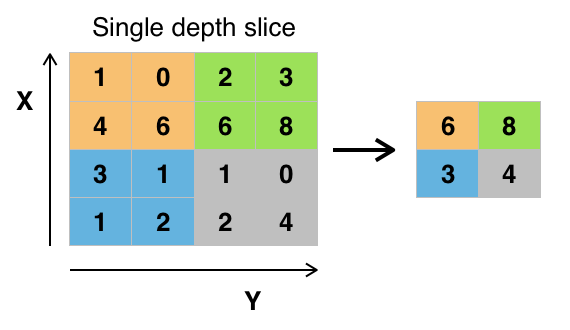
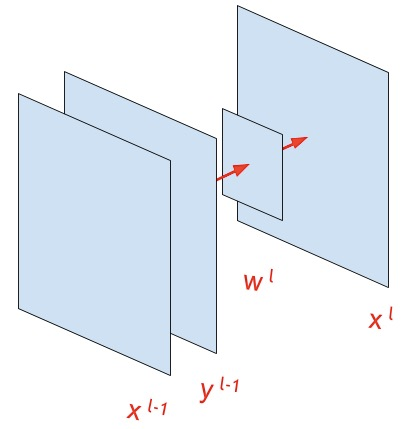
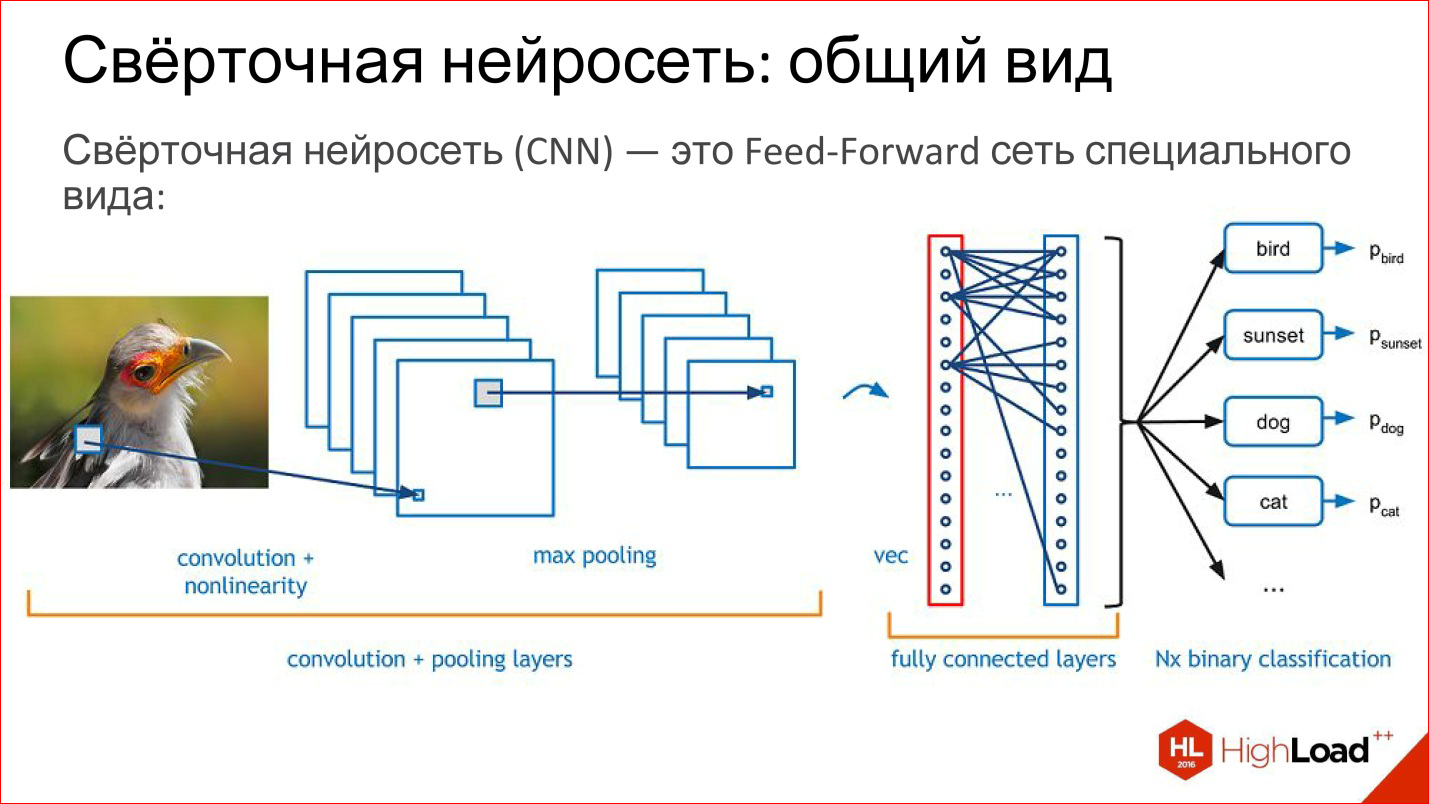
Сверточные сети
Сверточные сети
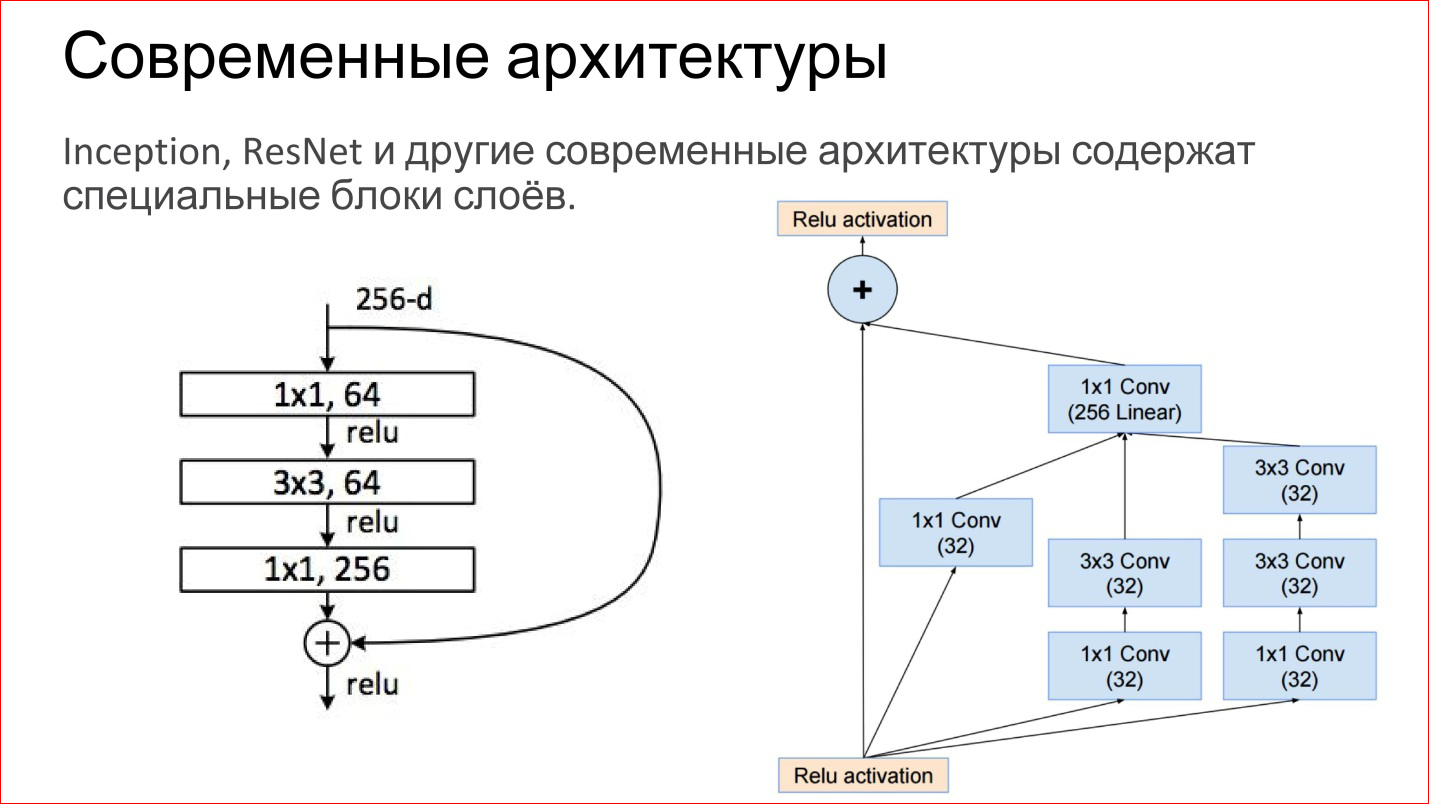
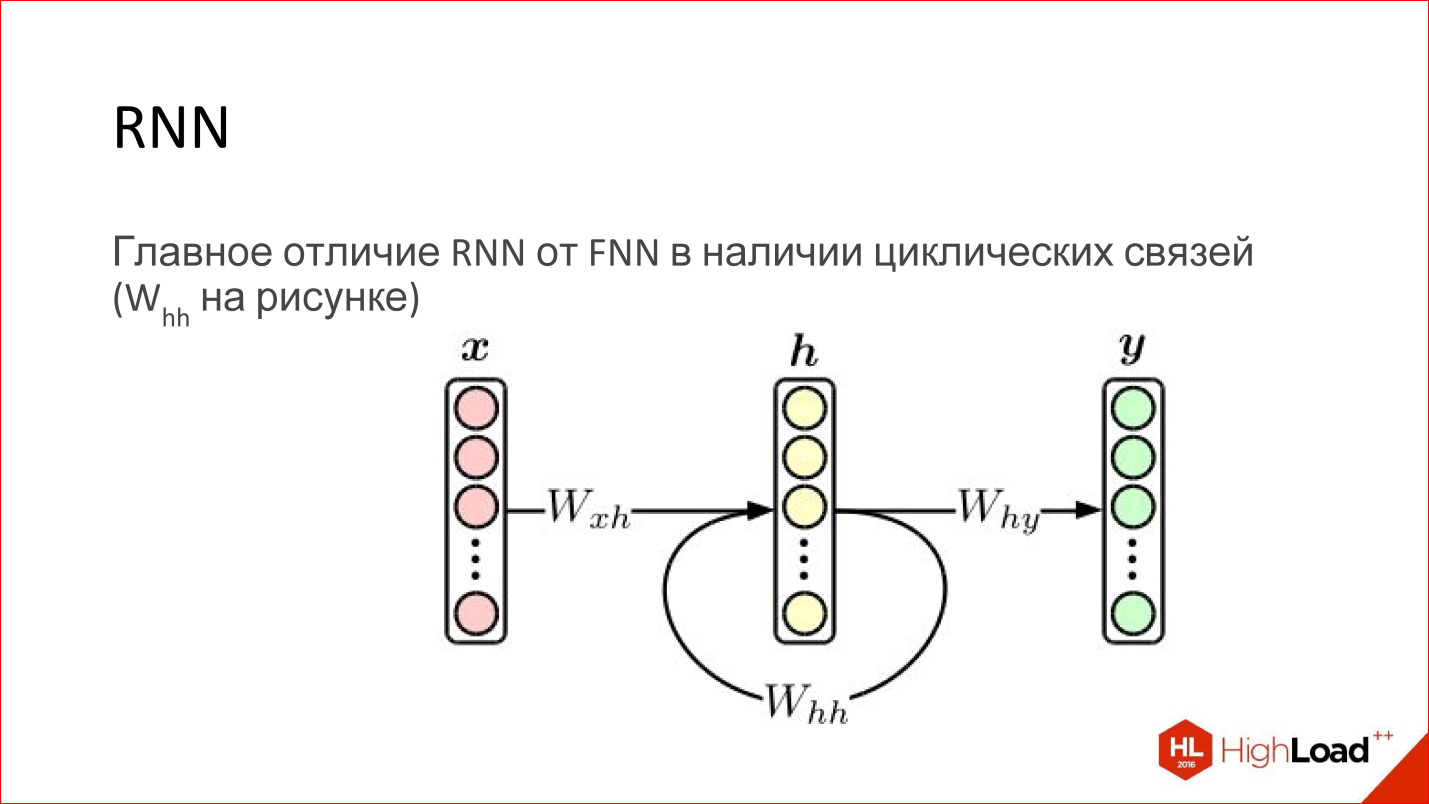
Рекуррентные нейросети
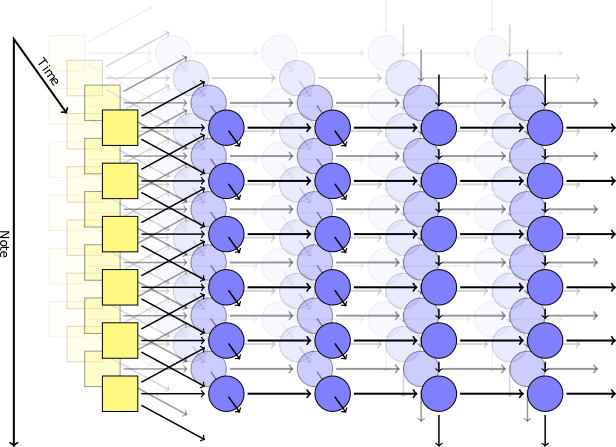
Рекуррентные нейросети
Введение в keras
Серьезное исследование

Атаки на нейросети
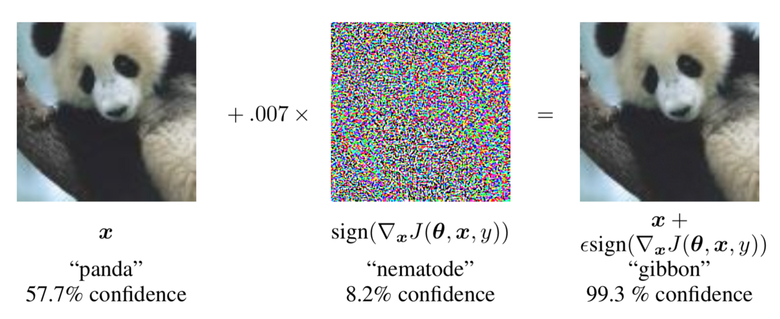
Ошибочная классификация
\(w^{\top }\widetilde{x}=w^{\top }x + w^{\top }\eta\)
Атака одного пикселя

Атаки-заплатки

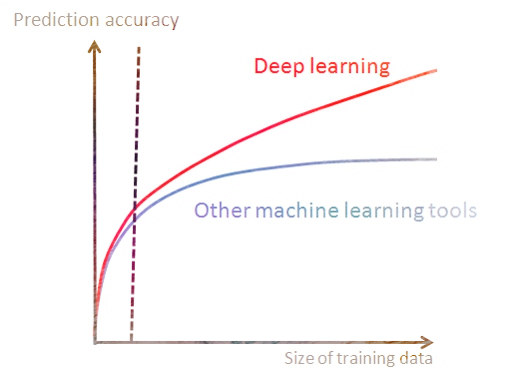
Кривые обучения
Распознавание лиц
Задание на лабу
- собрать набор фотографий участников вашей команды
- обучить нейронку так, чтобы она хорошо классифицировала новые фотографии участников
Рекомендация: сохранить модель или ее веса с помощью методов save или save_weights, чтоб на защите ее быстро подгрузить
Нейросети
By romvano
Нейросети
- 1,124



