Линейные методы
Среднеквадратичная ошибка
MSE(a, X) = \frac{1}{l} \sum_{i=1}^{l}{(a(x_i) - y_i)^2}
a_{опт} (x) = argmin_x Q(a, X)
Линейные модели
a(x) = w_0 + \sum_{j=1}^{d}w_jx^j
\(w_j\) - вес j-го признака;
\(x^j\) - значение j-го признака;
\(w_0 = const\)
Линейные модели
a(x) = \sum \limits_{j=1}^{d+1}w_jx^j = \langle w, x \rangle
\(w_j\) - вес j-го признака;
\(x^j\) - значение j-го признака;
\(w_0 = w_0 x^0\)
Добавим константный признак \(x_0 = 1\)
Среднеквадратичная ошибка
Q(w, X) = \frac{1}{l} \sum \limits_{i=1}^{l} (\langle w, x_i \rangle - y_i)^2
\(w\) - вещественный вектор весов модели;
\(x_i\) - вектор значений признаков объекта;
\(y_i\) - истинный ответ для i-го объекта;
\(l\) - количество объектов выборки
Задача регрессии
Q(w, X) = \frac{1}{l} \sum \limits_{i=1}^{l} (\langle w, x_i \rangle - y_i)^2 \rightarrow \min \limits_{w}
- d неизвестных
- константный признак
- выпуклая функция (т.к. ср.кв. ошибка)
Q(w, X) = \frac{1}{l} ||Xw - y||^2 \rightarrow \min \limits_{w}
Аналитическое решение
Q(w, X) = \frac{1}{l} ||Xw - y||^2 \rightarrow \min \limits_{w}
w_{опт} = (X^T X)^{-1}X^Ty
- вычислительно затратно по времени обращать матрицу при большом количестве признаков и на большой выборке
Градиентный спуск
\vec{w}^{[t]} = \vec{w}^{[t-1]} - \eta_t \nabla Q(\vec{w}^{[t-1]}, X)
||w^{[t]} - w^{[t-1]}|| < \epsilon - ?
w^{[0]} = 0
t = 1, 2, 3...
Инициализируем веса нулями:
Итерируемся, пока изменение весов на \(\eta_t\) в сторону антиградиента значимо:
Градиентный спуск для линейной регрессии
Рассмотрим случай с одним признаком:
\( a(x) = w_0 + w_1 x \)
Q(w_0, w_1, X) = \frac{1}{l} \sum \limits_{i=1}^{l} (w_1x_i + w_0 - y_i)^2
\frac{\partial Q}{\partial w_1} = \frac{2}{l} \sum \limits_{i=1}^{l} (w_1x_i + w_0 - y_i)x_i
\frac{\partial Q}{\partial w_0} = \frac{2}{l} \sum \limits_{i=1}^{l} (w_1x_i + w_0 - y_i)
Градиентный спуск для линейной регрессии
Градиентный спуск для линейной регрессии
Градиентный спуск для линейной регрессии - ошибки
Стохастический градиентный спуск
\nabla_w Q(w, X) = \frac{2}{l} X^T(Xw - y)
В обычном градиентном спуске:
\frac{\partial Q}{\partial w_j} = \frac{2}{l} \sum \limits_{i=1}^{l} x_i^j (\langle w, x_i \rangle - y_i)
- проход по всей выборке
Стохастический градиентный спуск
\vec{w}^{[t]} = \vec{w}^{[t-1]} - \eta_t \nabla Q(\vec{w}^{[t-1]}, \{x_i\})
\(x_i\) - случайный объект из выборки
Правдоподобие выборки
Как оценить неизвестный параметр по выборке?
Метод максимума правдоподобия
Пусть \(X \sim F(x, \theta) \),
\(\theta\) - неизвестные параметры распределения
X^N = (X_1, X_2, ..., X_n)
L(X^N, \theta) \equiv \prod \limits_{i=1}^{n} P(X = X_i, \theta)
\theta_{ОМП} = {argmax} _{\theta} L(X^n, \theta)
Метод максимума правдоподобия
L(X^N, \theta) \equiv \prod \limits_{i=1}^{n} P(X = X_i, \theta)
ln L(X^N, \theta) \equiv \sum \limits_{i=1}^{n} ln P(X = X_i, \theta)
\theta_{ОМП} = {argmax}_{\theta} lnL(X^n, \theta)
Сумму легче оптимизировать, чем произведение
Метод наименьших квадратов
Q(a, X) = \frac{1}{l} \sum \limits_{i=1}^{l}{(a - y_i)^2}
a_{опт} = argmin_a Q(a, X)
Пусть \(a\) - константа
Q(a) = \int \limits_{t}(a - t)^2 y(t)dt
Пусть мы знаем распределение \(y \sim y(t) \)
a_{опт} = argmin_a Q(a) = \mathbb{E} y
Какое \(a\) оптимально?
Метод наименьших квадратов
Теперь более общий случай. Пусть \(a\) - функция от \(x\)
Q(a) = \int \limits_{t}(a(x) - t)^2 y(t)dt
Пусть мы знаем распределение \(y \sim y(t) \)
a_{опт} = argmin_a Q(a) = \mathbb{E} (y|x)
Q(a(x), X) = \frac{1}{l} \sum \limits_{i=1}^{l}(a(x_i) - y_i)^2
Перейдем к конечной выборке
Q(w, X) = \frac{1}{l} \sum \limits_{i=1}^{l}(\langle w, x_i \rangle - y_i)^2
Лучшая аппроксимация минимума ошибки
Q(a(x), X) = \frac{1}{l} \sum \limits_{i=1}^{l}(a(x_i) - y_i)^2
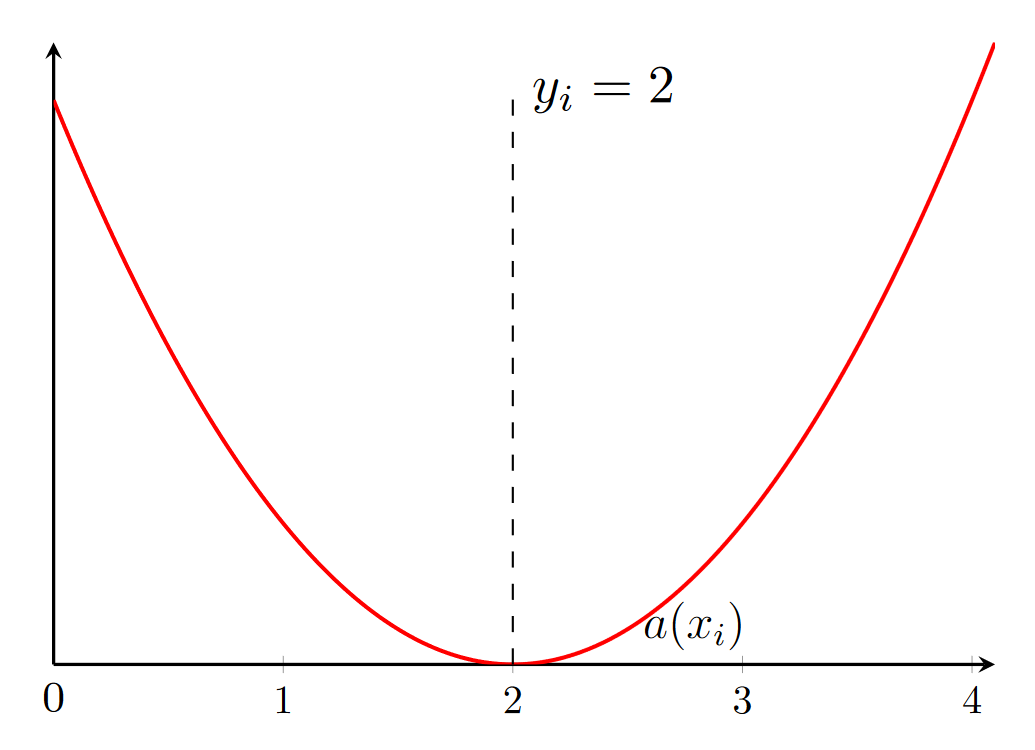
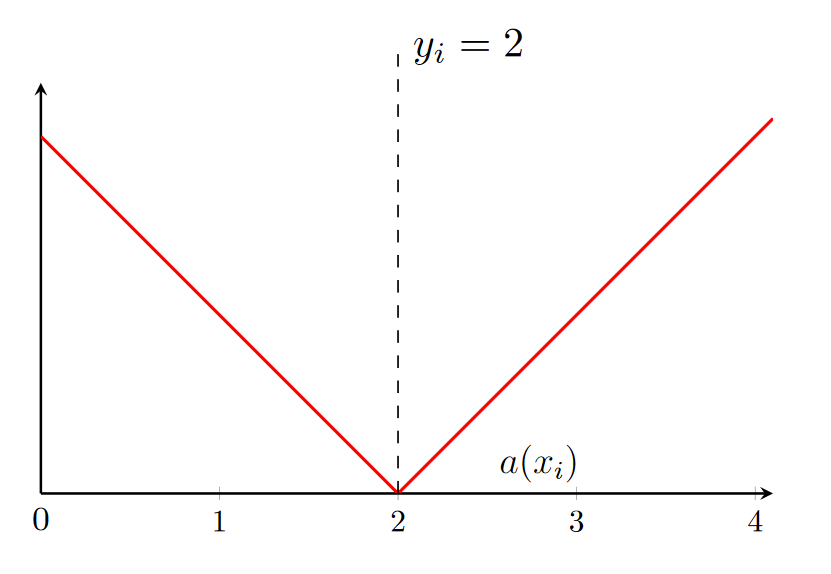
Ошибка
Q(a(x), X) = \frac{1}{l} \sum \limits_{i=1}^{l}|a(x_i) - y_i|
argmin_a Q(a) = \mathbb{E} (y|x)
argmin_a Q(a) = med(y|x)
Переобучение линейных моделей
Регуляризация
- Большие веса переобученной модели
- Идея: включить их в функционал ошибки, чтобы минимизировать не только отклонения ответов, но и веса модели
\(L_2\)-регуляризация
Будем минимизировать сумму квадратов весов: \(||w||^2 = \sum\limits_{j=1}^{d}w_j^2 \)
Q(w, X) + \lambda ||w||^2 \rightarrow \min\limits_w
- Чем \(\lambda\) больше, тем модель проще
- Чем \(\lambda\) меньше, тем выше риск переобучения
\(L_2\)-регуляризация
Q(w, X) + \lambda ||w||^2 \rightarrow \min\limits_w
То же самое:
Q(w, X) \rightarrow \min\limits_w
\\
||w||^2 \le C
\(L_1\)-регуляризация
Будем минимизировать сумму модулей весов: \(||w||_1 = \sum\limits_{j=1}^{d}|w_j| \)
Q(w, X) + \lambda ||w||_1 \rightarrow \min\limits_w
- Чем \(\lambda\) больше, тем модель проще, при этом могут занулиться некоторые признаки (при совсем большом \(\lambda\) - все)
- Чем \(\lambda\) меньше, тем выше риск переобучения
Выбор типа регуляризации
\(L_2\)-регуляризатор:
- штрафует модель за сложность
- гладкий и выпуклый - легко проводить минимизацию градиентными методами
\(L_1\)-регуляризатор:
- негладкий - сложнее оптимизировать
- зануляет признаки
- позволяет проводить отбор признаков
Линейная классификация
Линейный классификатор
a(x) = sign \sum \limits_{j=1}^{d+1} w_j x^j = sign \langle w, x \rangle
\(\langle w, x \rangle = 0 \)
уравнение гиперплоскости
Отступ
Будем решать задачу бинарной классификации на множество классов \(Y = \{-1, +1\}\)
M_i = y_i \langle w, x_i \rangle
\frac{\langle w, x_3 \rangle}{||w||}
\(M_i > 0\) - правильный ответ
\(M_i < 0\) - неправильный ответ
Чем больше отступ, тем больше уверенность
Метрики качества
Доля неправильных ответов:
Q(a, X) = \frac{1}{l} \sum \limits_{i=1}^{l}[y_i \langle w, x_i \rangle < 0]
Q(a, X) = \frac{1}{l} \sum \limits_{i=1}^{l}[M_i < 0]
Пороговая функция потерь
Снова та же проблема - сложно оптимизировать
Пороговая функция потерь
Возьмем гладкую оценку пороговой функции:
[M_i < 0] \le \widetilde L(M)
Оценим ее через функционал ошибки:
Q(a, X) \le \widetilde Q(a, X) = \frac{1}{l} \sum \limits_{i=1}^{l}\widetilde L(M_i) \rightarrow \min \limits_a
Минимизируем верхнюю оценку и надеемся, что пороговая функция потерь тоже уменьшится
Пороговая функция потерь
Логистическая функция потерь
\widetilde Q(a, X) = \frac{1}{l} \sum\limits_{i=1}^{l} ln(1+\exp(-M_i))
\widetilde Q(a, X) = \frac{1}{l} \sum\limits_{i=1}^{l} ln(1+\exp(-y_i \langle w, x_i \rangle))
- Отсюда можно выразить вероятность принадлежности объекта классу +1
Вероятность принадлежности классу
Хотим оценить \(P(y=1|x)\)
Введем \(\pi(x) = P(y=1|x)\)
\(\pi(x) = 1P(y=1|x)+0P(y=0|x)=\mathbb{E}(y|x) \)
Введем обобщенную линейную модель:
\(g(\mathbb{E}(y|x)) \approx \langle w, x\rangle \)
\( \mathbb{E}(y|x) \approx g^{-1}( \langle w, x\rangle) \)
Вероятность принадлежности классу
\mathbb{E}(y|x) = \pi(x) \approx \frac{e^{\langle w, x \rangle}}{1 + e^{\langle w, x \rangle}}
Вероятность принадлежности классу
\pi(x) \approx \frac{e^{\langle w, x \rangle}}{1 + e^{\langle w, x \rangle}}
\leftrightarrow
ln \frac{\pi(x)}{1 - \pi(x)} \approx \langle w, x \rangle
логит
Правдоподобие обучающей выборки
L(X) = \prod \limits_{i: y_i = 1} \pi(x_i) \prod \limits_{i: y_i = 0} (1 - \pi(x_i))
lnL(X) = \sum \limits_{i=1}^l \big( y_i ln\pi(x_i) + (1 - y_i) ln(1 - \pi(x_i)) \big)
Возьмем это выражение с минусом и переобозначим \(y = 0 \) за \(y = -1 \) - получим логистическую функцию потерь. А верхнее выражение - легко минимизировать
\widetilde Q(a, X) = \frac{1}{l} \sum\limits_{i=1}^{l} ln(1+\exp(-M_i))
Использование полиномиальных признаков в линейных моделях
Задание
- Обучить логистическую регрессию на своих данных, подобрать параметры.
- Сравнить результаты применения \(L_1\) и \(L_2\) регуляризаций. Посмотреть веса признаков, объяснить полученные значения.
- Провести отбор признаков с помощью \(L_1\) регуляризации, подобрать оптимальный C, объяснить результат.
Линейные методы
By romvano
