Логистическая регрессия. Линейная регрессия.
Метод опорных векторов. Обработка нечисловых данных
Логистическая регрессия
(это классификатор)
Логистическая регрессия
Будем решать задачу бинарной классификации на множество классов
\(Y = \{-1, +1\}\)
Построим линейный алгоритм:
\(a(\vec{x}, \vec{w}) = sign(\sum\limits_{j=1}^n w_j f_j(x) - w_0) = sign<\vec{x}^T, \vec{w}>\)
Будем минимизировать эмпирический риск:
\(Q(\vec{w}) = \sum\limits_{i=1}^m ln(1+\exp(-y_i <\vec{x_i}^T, \vec{w}>)) \rightarrow \min\limits_{\vec{w}}\)
Логистическая регрессия
Что всё это значит?
- Встать по будильнику в 7 утра или нет?
- Хочется спать
- Болит голова
- Хочется есть
- В универе важные пары
- На работе начальник приходит в этот день вовремя
-5
-3
+2
+4
+3
\(a(\vec{x}, \vec{w}) = sign<\vec{x}^T, \vec{w}>\)
Отступ

Откуда взялся логарифм?
Вероятность принадлежности объекта к классу +1:
Правдоподобие выборки:
А минимизировать проще сумму, чем произведение, поэтому берем логарифм от правдоподобия. Поскольку это монотонное преобразование, смысл задачи от этого не теряется
Преобразование для численной минимизации

График ошибки классификации от отсупа
Идея логистической регрессии

Построение линейной разделяющей гиперплоскости между классами
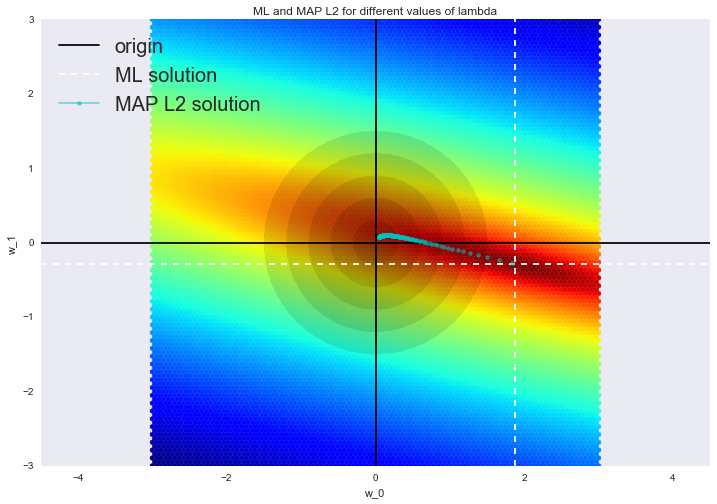
Регуляризация

Возможно переобучение модели из-за слишком больших весов w
Регуляризация
Будем минимизировать не только ошибку, но и веса
\(L_1\)-регуляризация:
\(Q(\vec{w}) + \frac{1}{C} \sum\limits_{j=0}^m |w_j| \rightarrow \min\)
\(L_2\)-регуляризация:
\(Q(\vec{w}) + \frac{1}{C} \sum\limits_{j=0}^m w_j^2 \rightarrow \min\)
Стохастический градиент
Линейная регрессия
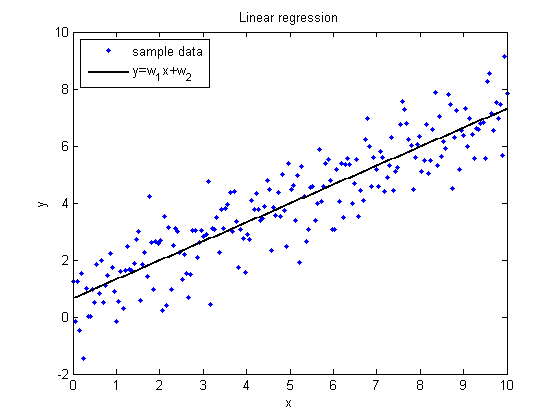
Линейная регрессия
Введем линейную модель предсказания значения целевой переменной в задаче регрессии:
\(y = w_0 + \sum\limits_{i=1}^m w_i x_i\)
Зададим модель:
\(\large \vec y = X \vec w+\epsilon\)
Ошибка регрессора будет складываться из квадратов ошибок каждого предсказания:
\( Q = \sum\limits_{i=1}^m L(y_i, a(x_i)) \) , где \(L(y_i, a(x_i)) = (y_i - a^2 (x_i)) \)
\(\large \begin{array}{rcl} \text{Err}\left(\vec{x}\right) = \left(f - \mathbb{E}\left[\hat{f}\right]\right)^2 + \text{Var}\left(\hat{f}\right) + \sigma^2 = \text{Bias}\left(\hat{f}\right)^2 + \text{Var}\left(\hat{f}\right) + \sigma^2 \end{array}\)
Ошибка линейной регрессии

\(\large \begin{array}{rcl} \text{Err}\left(\vec{x}\right) = \left(f - \mathbb{E}\left[\hat{f}\right]\right)^2 + \text{Var}\left(\hat{f}\right) + \sigma^2 = \text{Bias}\left(\hat{f}\right)^2 + \text{Var}\left(\hat{f}\right) + \sigma^2 \end{array}\)
Линейная регрессия и стохастический градиент
Метод опорных векторов
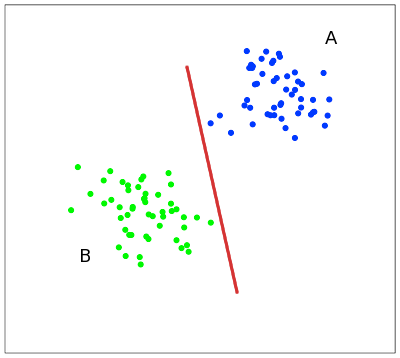

SVM - бинарный классификатор. Идет поиск разделяющей гиперплоскости, максимально отдаленной от объектов обоих классов
Метод опорных векторов
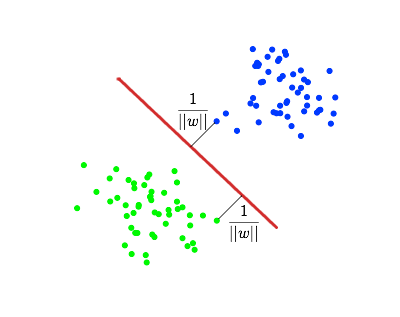
Линейная неразделимость

Метрики качества
| y = True | y = False | |
|---|---|---|
| a(x) = True | True Positive (TP) | False Positive (FP) |
| a(x) = False | False Negative (FN) | True Negative (TN) |

Метрики качества
Accuracy
\(\large accuracy = \frac{TP + TN}{TP + TN + FP + FN}\)
Precision и recall
\(\large precision = \frac{TP}{TP + FP}\)
\(\large recall = \frac{TP}{TP + FN}\)

F-мера
F = \(\frac{2*precision*recall}{precision+recall}\)
PR-кривая

b(x) оценивает принадлежность объекта классу
ROC-кривая

Чувствительность алгоритма - доля правильных положительных классификаций
Доля ошибочных положительных классификаций
Обработка текстов

TF-IDF
d - документ, D - множество документов, t - слово
Изображения
Аудио

Дата и время

Нормализация

Прочие преобразования признаков
Отбор признаков
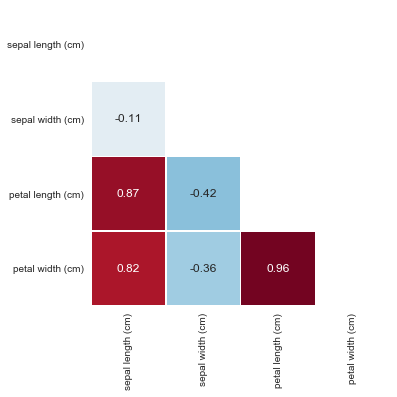
Задание
или
Или вместо того:
Логистическая и линейная регрессия. Опорные вектора
By romvano
Логистическая и линейная регрессия. Опорные вектора
- 434



