SCIST ALGO 240303

Complexity

Complexity

用以分析、表達一組計算流程的效率

用在哪？

  • 想到了新方法，到底是更快？更慢？
  • 你不會想花半小時寫完才發現會 TLE

Complexity 有兩種

  • Time complexity
  • Space complexity

沒特別講就是指 Time

空間是拿來交換時間用的

如何分析「時間」

其實不會真的拿時間作為單位

「時間」是不準的

例如「計算 n 數加總為何」

我的方法跑 1 秒，你的跑 2 秒，誰快？

時間受太多因素影響

  • 硬體優劣
  • 加總數字個數
  • 實作細節
  • 使用語言
  • 同時執行的其它程式
  • …etc

時間 = 計算量 / 速度

速度定義為每秒能做多少次計算

計算量與時間成正比

計算定義為 1 次的加減乘除或者比較大小

計算量是跑不掉的

不管你在什麼硬體下跑
該算 1000 次加法的，一次也跑不掉

資料量的影響

計算 100 數加總和 100000 數加總

所需計算量基本不會相同

資料量對計算量的關係

Complexity 的定義

f( 資料量 ) = 計算量

例如「計算 n 數加總為何」

ans = A_1 + A_2 + \ldots + A_n

需要 n-1 次加法，故

f(n) = n-1

f( 資料量 ) = 計算量

例如「判斷 n 數是否相異」

A_i \neq A_j

任意不相等 (i, j) 共 1+2+3+…+n 組，故

f(n) = \frac{n(n+1)}{2}

不同方法的優劣比較

怎樣定義哪個才是好的做法？

誰比較快？

f(n) = 1000n\\ g(n) = n^2
f(5) = 5000 > g(5) = 25\\ f(10^4) = 10^7 < g(10^4) = 10^8

計算量真那麼剛好嗎？

for (i=0, ans=0; i<n; i++)
{
	ans += ary[i];
}

考慮 i++、i<n、以及存取 ary[i] 隱含的位址計算…等

有些語言還會幫忙檢查 i 有沒有在正確範圍內C++: 關我屁事

不同計算也不會完全一樣快 加=減<乘<<<<<<除

重點：成長速度

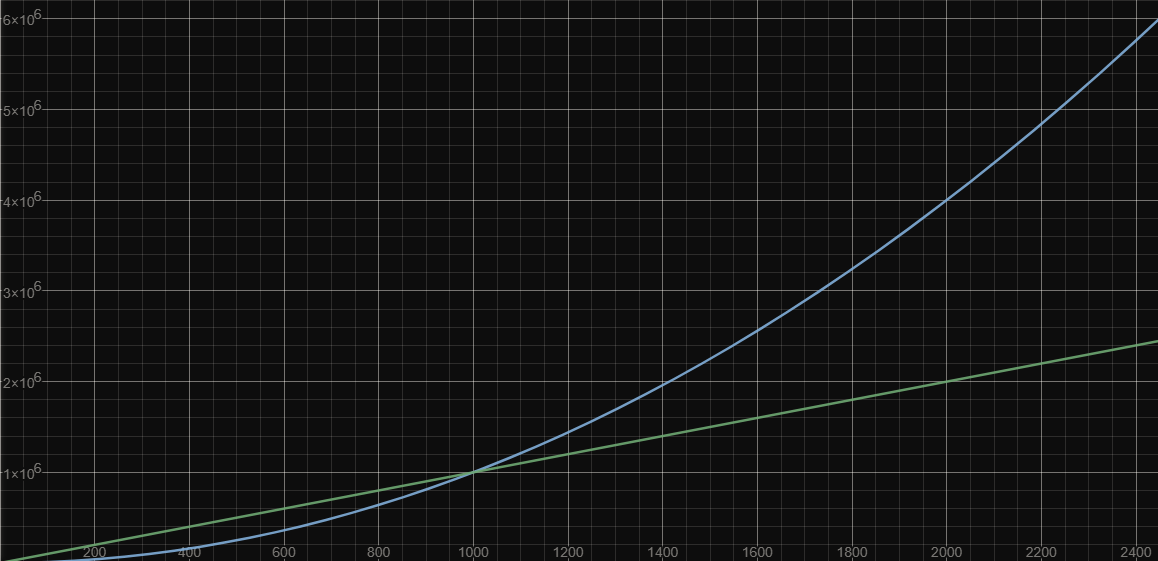
成長慢 = 資料量大時計算量較小 = 好方法

Big O 表記

取最高次項、去掉常數，表達成長速度

f(n) = n-1 記為 O(n) Linear Time
f(n) = 3n^2 - 2n + 7 記為 O(n^2)
f(n) = 10 記為 O(1) Constant Time

由於是表達成長速度 <= 的關係
所以 f(n) = n-1 記為 f(n) = O(n^2) 也不是不行
只是不夠精確所以意義不大

如何分析

怎麼從做法推出必要的計算量？

數迴圈

多層迴圈把每層最多執行幾次乘起來

不保證準，但大多時候準

 

並行的迴圈相加，多層的迴圈相乘
永遠考慮最糟情形

實際示範

int n, i, j;
int ary[1005];
cin >> n;
for (i=0; i<n; i++)
{
	cin >> ary[i];
}
bool duplicate = false;
for (i=0; i<n&&!duplicate; i++)
{
	for (j=i+1; j<n&&!duplicate; j++)
    {
    	if (ary[i] == ary[j])
        {
        	duplicate = true;
        }
    }
}
if (duplicate)
{
	cout << "no\n";
}
else
{
	cout << "yes\n";
}

最佳情形只要 1 次計算？
當它不會發生

複數變因影響計算量

都記，才能依不同資料性質，選用適合的方法

多變因示範一

int n, q, i, j;
int ary[1005];
cin >> n;
for (i=0; i<n; i++)
{
	cin >> ary[i];
}
cin >> q;
for (i=0; i<q; i++)
{
	int k;
	cin >> k;
    bool is_appear = false;
    for (j=0; j<n&&!is_appear; j++)
    {
    	if (ary[j] == k)
        {
        	is_appear = true;
        }
    }
    cout << is_appear << "\n";
}

多變因示範二

int n, q, i, j;
bool appear[1005] = {};
cin >> n;
for (i=0; i<n; i++)
{
	int t;
	cin >> t;
    appear[t] = true;
}
cin >> q;
for (i=0; i<q; i++)
{
	int k;
	cin >> k;
    cout << appear[k] << "\n";
}

如何估算時間

用來判斷是否會 TLE

計算最糟情形

例如 n <= 1000、時限 2 秒，複雜度 O(n^2)

代入得計算量最糟 1000^2 = 10^6

 

一般以每秒 10^8 次計算來估計

\frac{10^6}{10^8}=\frac{1}{100}

（秒）

AC

計算最糟情形

例如 n <= 100000、時限 2 秒，複雜度 O(n^2)

代入得計算量最糟 100000^2 = 10^10

 

一般以每秒 10^8 次計算來估計

\frac{10^{10}}{10^8}=100

（秒）

TLE

從題目限制逆推合理複雜度

  • n <= 10^18: O( 1 ) or O( log n )
  • n <= 10^9: O( n^0.5 )
  • n <= 10^6: O( n ) or O(n log n)
  • n <= 10^3: O( n^2 )
  • n <= 10^2: O( n^3 )
  • n <= 20: O( 2^n )
  • n <= 10: O( n! )

（作為參考但不限於這些）

如何壓低計算量

觀察特性，善加運用

迴避重複計算

相同的東西算一次就好

例題

給一多項式與 x 的值，求結果為何？

 

例 f( x ) = 6x^3 - 3x^2 + 7x - 16

給 x = 3 則

f( 3 ) = 6*27 - 3*9 + 7*3 - 16 = 140

直觀解

給一多項式與 x 的值，求結果為何？

 

例 f( x ) = 6x^3 - 3x^2 + 7x - 16

給 x = 3 則

f( 3 ) = 6*27 - 3*9 + 7*3 - 16 = 140

對每項個別計算後加總

k 次方項需 k+1 次乘法

計算量 (n+1) + n + (n-1) + ... + 1 = O(n^2)

觀察

6x^3 = 6 * x * x * x

3x^2 = 3 * x * x

找到重複計算，改用以下方式處理

x^k = x^{k-1}\times x

直觀解．改

給一多項式與 x 的值，求結果為何？

 

例 f( x ) = 6x^3 - 3x^2 + 7x - 16

給 x = 3 則

f( 3 ) = 6*27 - 3*9 + 7*3 - 16 = 140

對每項個別計算後加總
x^k 從 x^(k-1) 用 1 次乘法算出
每項需 2 次乘法

計算量 2 * (n+1) = O(n)

例題

對數列 A 求是否存在區間 [l, r] 總和為 k

 

例 A = {3, 7, 5, 6, 4}, k = 18

則存在 l = 2, r = 4 區間 {7, 5, 6} 即為所求

直觀解

對數列 A 求是否存在區間 [l, r] 總和為 k

 

例 A = {3, 7, 5, 6, 4}, k = 18

則存在 l = 2, r = 4 區間 {7, 5, 6} 即為所求

窮舉所有區間 [l, r]
對每區間計算總和

區間數約 n^2，計算區間總和 n 次加法
推得複雜度 O( n^3 )

觀察

sum(l, r) = A_l + A_{l+1} + \ldots + A_{r-1} + A_r\\ sum(l, r+1) = A_l + A_{l+1} + \ldots + A_{r-1} + A_r + A_{r+1}

推得

sum(l, r+1) = sum(l, r) + A_{r+1}

直觀解．改

對數列 A 求是否存在區間 [l, r] 總和為 k

 

例 A = {3, 7, 5, 6, 4}, k = 18

則存在 l = 2, r = 4 區間 {7, 5, 6} 即為所求

窮舉所有區間 [l, r]
對每區間 [l, r] 利用 [l, r-1] 的總和來計算

區間數約 n^2，計算區間總和 1 次加法
推得複雜度 O( n^2 )

其實可以做到 O( n log n ) 不過會很複雜

節省不必要的窮舉

但要省大的
別為了省小的反而把 code 變複雜，得不償失

例題

求正整數 n 是否為質數

窮舉法

求正整數 n 是否為質數

根據定義 n 若為質數時，因數僅有 1 和 n
故 2 到 n-1 必不存在其它因數

窮舉 2 到 n-1 檢查是否為 n 的因數

複雜度 O(n)

觀察

設 i 為 n 的因數
可知存在正整數 j 使得 i * j = n
又因為 i 是正整數，故 j 也是 n 的因數
可知因數成對出現

因此只須窮舉 i 使得 i <= n/i 來避免重複
移項可得 i*i <= n 故 i <= sqrt( n )

窮舉法．改

求正整數 n 是否為質數

根據定義 n 若為質數時，因數僅有 1 和 n
故 2 到 n-1 必不存在其它因數

窮舉 2 到 sqrt( n ) 檢查是否為 n 的因數

複雜度              

O(\sqrt n)

例題

求用 3、5 元硬幣任意多個，湊 n 元的方法數

暴力解

求用 3、5 元硬幣任意多個，湊 n 元的方法數

等價於求存在多少非負整數數對 (x, y)
滿足 3x + 5y = n

可知 x <= n/3, y <= n/5
窮舉 x, y 所有可能範圍

複雜度 O( n^2 )

觀察

對窮舉的 x 由 n = 3x + 5y 可知

y = \frac{(n-3x)}{5}

若 n - 3x 非負、且為 5 的倍數
則 y 有唯一的非負整數解，無須窮舉

暴力解．改

求用 3、5 元硬幣任意多個，湊 n 元的方法數

等價於求存在多少非負整數數對 (x, y)
滿足 3x + 5y = n

可知 x <= n/3, y <= n/5
窮舉範圍較小的 y 所有可能範圍
判斷 n - 5y 是否為 3 的倍數，需要 1 次除法

複雜度 O( n )

善用 bucket

適合用在數字個數多、範圍小時

例題

給數列 A 求有幾組數對 (i, j)
使 Ai - Aj 為 200 的倍數

暴力解

給數列 A 求有幾組數對 (i, j)
使 Ai - Aj 為 200 的倍數

窮舉所有可能數對 (i, j)
檢查是否為 200 的倍數

複雜度 O( n^2 )

觀察

若 x - y 為 200 倍數
則 x, y 除以 200 的餘數必相同

故將除以 200 同餘放在一起、不同餘分開
餘數範圍為 0 到 199 可使用 bucket 計數

暴力解．改

給數列 A 求有幾組數對 (i, j)
使 Ai - Aj 為 200 的倍數

窮舉所有數字，將除以 200 餘數為 t 者
記錄於 B[t]

最後窮舉所有可能餘數
若有 k 個同餘，則每個可配其它 k-1 個
提供數對 k(k-1) 個

計算量 n + 200 複雜度 O( n )

找循環

例題

給正整數數列 A 將其重複串接許多次形成數列 B

求最小整數 i 使得 B[1] + B[2] + ... + B[i] > k

暴力解

給正整數數列 A 將其重複串接許多次形成數列 B

求最小整數 i 使得 B[1] + B[2] + ... + B[i] > k

窮舉答案 1, 2, 3, … 逐個計算
直到總和超過 k 時停下，此時 i 即為所求

最多窮舉 k 項，每項線性時間求加總

複雜度 O( k^2 )

暴力解．改

給正整數數列 A 將其重複串接許多次形成數列 B

求最小整數 i 使得 B[1] + B[2] + ... + B[i] > k

窮舉答案 1, 2, 3, … 逐個計算
直到總和超過 k 時停下，此時 i 即為所求

最多窮舉 k 項，每項總和只比前一項多 1 個數

複雜度 O( k )

觀察

n 雖然不大，但 k 可以很大
由於每 n 項會循環，可知

  • 1 到 n 項
  • n+1 到 2n 項
  • 2n+1 到 3n 項

等每 n 項的內容完全相同，因此總和也相同
將 A 數列加總為 s，則 k / s 即為循環幾次 n 項

暴力解．改二

給正整數數列 A 將其重複串接許多次形成數列 B

求最小整數 i 使得 B[1] + B[2] + ... + B[i] > k

求數列 A 總和 s
將 k 除以 s 取其商為 t 餘數 r
窮舉 i 加總至超過 r 為止
則 t*n + i 即為所求

最多窮舉 n 項，每項總和只比前一項多 1 個數

複雜度 O( n )

其它

難以分類的東西

例題

給一組只包含 0、1 的字串
求每個 0 離最近的 1 的距離中
最遠者距離多少

暴力解

給一組只包含 0、1 的字串
求每個 0 離最近的 1 的距離中
最遠者距離多少

窮舉字串中每個字
若它是 0，從它出發往左右找最近的 1
最後從每個 0 的距離中找出最大值

最多窮舉 n 個字，每個字最多找距離 n

複雜度 O( n^2 )

觀察

由左往右看時，一旦遇到新的 1
在它之後遇到的 0 往左時就會先撞新的 1
就撞不到所有更舊的 1

因此由左往右掃，記錄最後遇到的 1 在哪
對每個 0 記錄當下最後遇到的 1
可求得每個 0 左邊最近距離

由右往左掃則可以求每個 0 右邊最近距離

暴力解．改

給一組只包含 0、1 的字串
求每個 0 離最近的 1 的距離中
最遠者距離多少

由左到右窮舉字串中每個字
若它是 1，記錄為最後遇到的 1 的位置；
若它是 0，記左邊最後遇到的 1 的距離

上述再由右到左窮舉，找所有右邊最近 1 的距離

最後窮舉每個 0 判斷左右哪邊近，並求最近距離的最大值

窮舉 n 個字共 3（或者 4）次，每個字計算量 O( 1 )

複雜度 O( n )

Extra

迴圈相乘不準的例子：調和級數

例題

給數列 A 求是否存在 k 滿足
令 B = {A[k], A[2k], A[3k], ...}
B 至少有 2 個元素，且 B 為遞增序列

暴力解

給數列 A 求是否存在 k 滿足
令 B = {A[k], A[2k], A[3k], ...}
B 至少有 2 個元素，且 B 為遞增序列

窮舉 k = 1 .. n/2 檢查是否遞增
遞增序列須檢查是否所有 i 皆滿足 B[i] >= B[i-1]
計算量為線性

窮舉 n 種 k，每種最糟 n 的計算量
複雜度為 O( n^2 )

雖然沒錯

以 Big O 表記而言
計算量確實絕對在 n^2 以內

實際計算量應為

\frac{n}{1} + \frac{n}{2} + \frac{n}{3} + \ldots + \frac{n}{n}

衰減速度非常快

調和級數

以上數列不好計算，但可以找新的天花板
將每項向上提到分母為 2 的次方數，可得

\frac{n}{1} + \frac{n}{2} + \frac{n}{3} + \ldots + \frac{n}{n}
\begin{aligned} &\frac{n}{1} + \frac{n}{2} + \frac{n}{3} + \frac{n}{4} + \frac{n}{5} + \frac{n}{6} + \frac{n}{7} + \frac{n}{8} + \ldots + \frac{n}{n}\\ \leq&\frac{n}{1} + \frac{n}{2} + \frac{n}{2} + \frac{n}{4} + \frac{n}{4} + \frac{n}{4} + \frac{n}{4} + \frac{n}{8} + \ldots + \frac{n}{n}\\ \leq&\frac{n}{1}\times 1 + \frac{n}{2}\times 2 + \frac{n}{4}\times 4 + \ldots + \frac{n}{2^k}\times 2^k\\ =&n \times (k+1)\\ \end{aligned}

又 n 約為 2^k 故

n = 2^k \Rightarrow k = \log_2 n

調合級數

\frac{n}{1} + \frac{n}{2} + \frac{n}{3} + \ldots + \frac{n}{n}\leq n\log_2 n

結論：

故複雜度更精確為 O( n log n )

歡樂練習時間

SCIST240303_Complexity

By sa072686

Made with Slides.com

SCIST240303_Complexity

  • 246

More from sa072686