SCIST ALGO 240317
Recursion
遞迴
遞迴只應天上有，凡人該當用迴圈
尋找相似子結構
找出原問題的答案與相似子問題的關係
同性質子問題
設 f( n ) = 1 x 2 x 3 x 4 x ... x n 則
- f( 4 ) = 1 x 2 x 3 x 4
- f( 5 ) = 1 x 2 x 3 x 4 x 5
由上，可發現 f( 5 ) 中的部份計算
與 f( 4 ) 完全相同
故 f( 5 ) 的結果，可由 f( 4 ) 算出
f( 5 ) = f( 4 ) x 5
問題變成：必須先知道 f( 4 )
同性質，所以同算法
設 f( n ) = 1 x 2 x 3 x 4 x ... x n 則
- f( 3 ) = 1 x 2 x 3
- f( 4 ) = 1 x 2 x 3 x 4
由上，可發現 f( 4 ) 中的部份計算
與 f( 3 ) 完全相同
故 f( 4 ) 的結果，可由 f( 3 ) 算出
f( 4 ) = f( 3 ) x 4
問題變成：必須先知道 f( 3 )
一般化
f( 5 ) = f( 4 ) x 5
f( 4 ) = f( 3 ) x 4
可推得
f( i ) = f( i-1 ) x i
f( i ) 依賴於 f( i-1 )
直到回歸初始定義 f( 0 ) = 1
即可一層一層推回原問題
實作方法
- Top-down：由原問題需求出發
- Bottom-up：從已知最小問題出發
Bottom-up
從已知 f( 0 ) 開始
f(1) = f(0)\times 1 = 1\times 1 = 1\\
f(2) = f(1)\times 2 = 1\times 2 = 2\\
f(3) = f(2)\times 3 = 2\times 3 = 6\\
f(4) = f(3)\times 4 = 6\times 4 = 24\\
f(5) = f(4)\times 5 = 24\times 5 = 120\\
f[0] = 1;
for (int i=1; i<=n; i++)
{
f[i] = f[i-1] * i;
}Top-down
f( 5 ) 需要 f( 4 )，先求 f( 4 )
f( 4 ) 需要 f( 3 )，先求 f( 3 )
f( 3 ) 需要 f( 2 )，先求 f( 2 )
f( 2 ) 需要 f( 1 )，先求 f( 1 )
f( 1 ) 需要 f( 0 )，先求 f( 0 )
f( 0 ) 已知，回推
int f(int i)
{
if (i == 0)
{
return 1;
}
return f( i-1 ) * i;
}找出關係式 = 已解出
不用找到直接解
有關係式就夠求解了
（原問題和相似子問題間的關係）
和平常學的解題方向不同
需要適應這個思考方式
遞迴解的流程
- 拆解問題，找到相似子問題
- 找出原問題和子問題關係
- 定義函數來表達問題與關係
- 找出最小的已知（邊界）問題
- AC
例題：費氏數列
求存在多少種以 1 和 2 構成的序列
使序列總和恰為 n
例如 n = 5 答案為 8
- 11111
- 1112
- 1121
- 1211
- 2111
- 122
- 212
- 221
觀察
序列最後一個元素依題意必為 1 或者 2
設總和為 5 時
窮舉所有可能的最後元素如下
\begin{cases}
A_1 + A_2 + \ldots + A_k + 1 = 5\\
A_1 + A_2 + \ldots + A_k + 2 = 5
\end{cases}
整理一下可得
\begin{cases}
A_1 + A_2 + \ldots + A_k = 5 - 1 = 4\\
A_1 + A_2 + \ldots + A_k = 5 - 2 = 3
\end{cases}
尋找相似結構
設總和為 5 時
\begin{cases}
A_1 + A_2 + \ldots + A_k + 1 = 5\\
A_1 + A_2 + \ldots + A_k + 2 = 5
\end{cases}
可知任意一組序列總和為 4 時，
末尾補上 1 即可湊出一組總和為 5
同理任意一組序列總和為 3 時，
末尾補上 2 即可湊出一組總和為 5
設序列總和為 4 共 x 組
序列總和為 3 共 y 組
則序列總和為 5 共 x * 1 + y * 1 組
問題轉換
原問題：求有多少序列總和為 5
轉變為
- 求有多少序列總和為 4
- 求有多少序列總和為 3
將上述答案加總，即為所求
設 f( n ) = 有多少序列總和為 n
由上述觀察，可列式表達關係為
f(n) = f(n-1) + f(n-2)
注意子問題的重疊
f(5) = \begin{cases}
f(4) = \begin{cases}
f(3) = \begin{cases}
f(2) = \begin{cases}
f(1) = 1\\
f(0) = 1
\end{cases}\\
f(1) = 1
\end{cases}\\
f(2) = \begin{cases}
f(1) = 1\\
f(0) = 1
\end{cases}\\
\end{cases}\\
f(3) = \begin{cases}
f(2) = \begin{cases}
f(1) = 1\\
f(0) = 1
\end{cases}\\
f(1) = 1
\end{cases}
\end{cases}
Top-down 共計 15 次 function call
其實只有 6 項
重複的子問題
f( 3 ) 算幾次都是 3
f( 2 ) 算幾次都是 2
每次重算幹嘛？
設 g( i ) 為：計算 f( i ) 所需 function call 次數
g(0) = 1\\
g(1) = 1\\
g(i) = 1 + g(i-1) + g(i-2)
f(5) = \begin{cases}
f(4) = \begin{cases}
\ldots
\end{cases}\\
f(3) = \begin{cases}
\ldots
\end{cases}
\end{cases}
記錄答案避免重算
int f(int i)
{
if (i <= 1)
{
return 1;
}
return f(i-1) + f(i-2);
}int f(int i)
{
if (used[i])
{
return rec[i];
}
used[i] = true;
if (i <= 1)
{
return rec[i] = 1;
}
return rec[i] = f(i-1) + f(i-2);
}無記錄 Top-down
有記錄 Top-down
※Bottom-up 無此問題
快速冪
有效率地計算
a^b
計算 a 的 b 次方
設
由
觀察可得
f( a, b ) = a \times a \times a \times \ldots \times a = a^b
f( a, b ) = f( a, b-1 ) \times a
a^b = a^{b-1}\times a
好像跟直接算沒什麼差別？
觀察
\begin{aligned}
f(a, 6) &= a\times a\times a\times a\times a\times a\\
&= (a\times a\times a)\times (a\times a\times a)\\
&= a^3\times a^3\\
&= f(a, 3)\times f(a, 3)
\end{aligned}
總之折半看看
奇數無法折剛好，怎辦
那就別折，套
f( a, b ) = f( a, b-1 ) \times a
若 b 為奇數，則 b-1 為偶數，可折半
計算 a 的 b 次方
設
f( a, b ) = a \times a \times a \times \ldots \times a = a^b
可得關係式
\begin{aligned}
f(a, b) = \begin{cases}
f(a, \frac{b}{2})^2 & , if\ b\%2= 0\\
f(a, b-1)\times a & , else
\end{cases}
\end{aligned}
最多每 2 次計算使 b 減半
設 k 為使 b 回到 0 所需「減半」次數，則
f(a, 0) = 1
\begin{aligned}
&\frac{b}{2^k}<1\\
\Rightarrow& \ b<2^k\\
\Rightarrow& \log_2 b < k
\end{aligned}
複雜度
最差 2 x log b 次的計算
O(\log_2 b)
實作注意
必須將 f( a, b/2 ) 的計算結果存下
若呼叫 2 次，複雜度會直接爛掉
int f(int a, int b)
{
if (b == 0)
{
return 1;
}
if (b % 2 != 0)
{
return f(a, b-1) * a;
}
int t = f(a, b/2);
return t * t;
}例題
Kattis batmanacci
題意
給 n, k 定義序列 S 如下
S_1 = "N"\\
S_2 = "A"\\
S_i = S_{i-2} + S_{i-1}
定義加法為將兩字串串接成新的字串
求 Sn 的第 k 個字元為何？
n\leq 10^5\\
k\leq 10^{18}
觀察
k 最大為 1e18 表示 S[n] 最長可到 1e18
→ 算出 S[n] 的全貌是不可能的
考慮 S[n] 由 S[n-2] 和 S[n-1] 構成
故 S[n] 中的任何文字，只有 2 種可能來源
- 由 S[n-2] 提供
- 由 S[n-1] 提供
S[n] 的第 k 文字
設 L[n] 為 S[n] 的長度
可知若 k <= L[n-2] 時
S[n] 的第 k 字由 S[n-2] 提供
位置同樣為 k
若 k > L[n-2] 時
S[n] 的第 k 字由 S[n-1] 提供
位置為 k - L[n-2]
S[5] = NAANA
S[6] = ANANAANA
S[7] = NAANAANANAANA
關係式
定義 f( n, k ) 為 S[n] 第 k 個字
\begin{aligned}
f(n, k) = \begin{cases}
f(n-2, k) & , k\leq L_{n-2}\\
f(n-1, k-L_{n-2}) & , k > L_{n-2}
\end{cases}
\end{aligned}
f(1, 1) = "N"\\
f(2, 1) = "A"
L[n] 的關係
S[n] 由 S[n-1] 和 S[n-2] 串接而成
故長度也會是 S[n-1] 長度加上 S[n-2] 長度
L_n = L_{n-2} + L_{n-1}
L_1 = 1\\
L_2 = 1
問題：L 的成長為費氏數列
費氏數列的成長速度約 2^n
大約 40 項爆 int
大約 90 項爆 long long
觀察
\begin{aligned}
f(n, k) = \begin{cases}
f(n-2, k) & , k\leq L_{n-2}\\
f(n-1, k-L_{n-2}) & , k > L_{n-2}
\end{cases}
\end{aligned}
L 主要用在判是否比 k 大
善用遞移律可知若 L[n-2] >= 10^18
又 k <= 10^18
故 L[n-2] >= k
結論：任何比 10^18 大的 L
和 10^18 作用相等
實作
const long long LIMIT = 1e18 + 5;
len[1] = 1;
len[2] = 1;
for (int i=3; i<=n; i++)
{
len[i] = min(LIMIT, len[i-1]+len[i-2]);
}求 L
char f(int n, long long k)
{
if (n == 1)
{
return 'N';
}
if (n == 2)
{
return 'A';
}
if (k <= len[n-2])
{
return f(n-2, k);
}
return f(n-1, k-len[n-2]);
}求原問題
另解
n 只要約 90+ 時，L[n-2] 就會超過 k 對吧…？
O(1) 解
\begin{aligned}
f(n, k) = \begin{cases}
f(n-2, k) & , k\leq L_{n-2}\\
f(n-1, k-L_{n-2}) & , k > L_{n-2}
\end{cases}
\end{aligned}
可知若 L[n-2] 超過 1e18 時
必走 n 減少 2、而 k 不變的分歧
故奇偶不變
若 L[n-2] 超過 1e18 的邊界為 n = 100
則超過 100 的 n 必會跑到 100
超過 99 的 n 必會跑到 99
故可依奇偶直接回到 n = 99 或 100
剩下照舊跑完
達成計算量與 n 無關最多 100 = O(1)
例題
UVa 839
題意
給一個天秤，左右可能為子天秤或砝碼
子天秤的話重量為其底下所有砝碼總和
求是否所有子天秤皆平衡
平衡定義為兩邊的力矩乘上重量相等
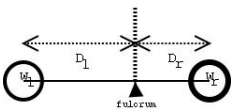
當 W[l] x D[l] = W[r] x D[r] 時平衡
輸入示意
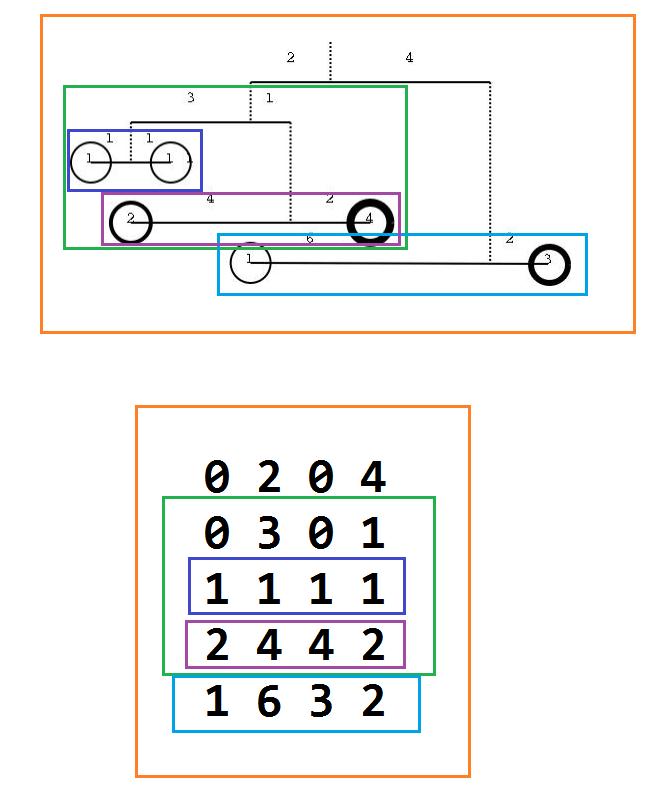
尋找子結構
由於天秤平衡需由兩側重量計算
定義 f 處理一層天秤
則左或右為天秤時，遞迴呼叫 f 處理
並丟回重量
平衡可由全域 bool 判定全平衡/至少一失衡
示意
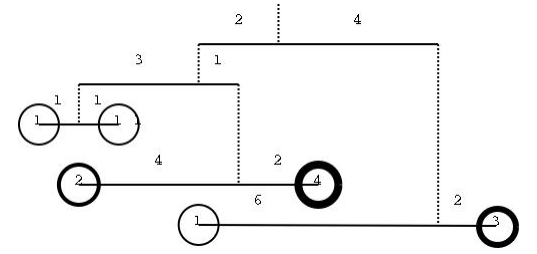
實作示意
bool imba = false;
int f()
{
int wl, dl, wr, dr;
cin >> wl >> dl >> wr >> dr;
if (wl == 0)
{
wl = f();
}
if (wr == 0)
{
wr = f();
}
imba |= (wl * dl != wr * dr);
return wl + wr;
}例題
ZJ f640
題意
給三函數
f(x) = 2x-3\\
g(x, y) = 2x + y - 7\\
h(x, y, z) = 3x - 2y + z
再給以此三函數組成的運算式，求解
例 h f 5 g 3 4 3
代表 ℎ( 𝑓(5), 𝑔(3, 4), 3 ) = 18
觀察
例如 f f f 2
本質為 f ( x )
在這裡 x 為 f f 2
為相似子問題
定義 t() 計算下個值為何
以 f f f 2 為例，解讀為
t("f f f 2") = f( x = t("f f 2") )
找到相似子結構
觀察
例如 h f 5 g 3 4 3
則 t( "h f 5 g 3 4 3" ) = h( ?, ?, ? )
不知道怎麼切分
就讓 t 只找到下個值為止
h( t( "f 5 g 3 4 3" ) )
= h( f( t( "5 g 3 4 3" ) ) )
= h( f( 5 ), t( "g 3 4 3" ) )
= h( f( 5 ), g( t( "3 4 3" ) ) )
= h( f( 5 ), g( 3, t( "4 3" ) ) )
= h( f( 5 ), g( 3, 4 ), t( "3" ) ) )
= h( f( 5 ), g( 3, 4 ), 3 ) )
stack 概念，下個值給後出現函數
湊夠就合成一個值往上一層丟
實作示意
int t()
{
string s;
cin >> s;
if (s == "f")
{
int x = t();
return x*2 - 3;
}
else if (s == "g")
{
int x = t();
int y = t();
return x*2 + y - 7;
}
else if (s == "h")
{
int x = t();
int y = t();
int z = t();
return x*3 - y*2 + z;
}
return stol(s);
}例題
CSES 2165
河內塔
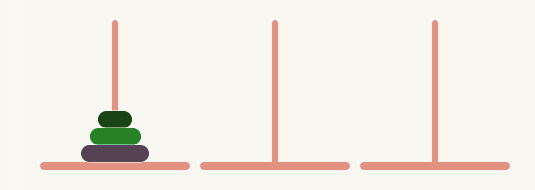
觀察
設將盤子大小 1、2、3 自 A 柱搬至 C 柱
最大的盤子 3 不得放在 1、2 之上
故盤子 3 必先搬至空的 C 柱上
又盤子 3 要搬動，必須先將盤子 1、2 移走
可得流程：
- 盤子 1、2 自 A 柱搬至不使用之 B 柱
- 盤子 3 自 A 柱搬至目標 C 柱
- 將剩下盤子 1、2 自 B 柱搬至 C 柱
定義關係
設 f( n, st, ed, mid ) 將 1~n 盤
自 st 柱搬至 ed 柱
f( n, st, ed, mid) 流程為
- f( n-1, st, mid, ed )
- 將 n 從 st 搬到 ed
- f( n-1, mid, ed, st )
實作示意
void f(int n, int st, int ed, int mid)
{
if (n == 0)
{
return ;
}
f(n-1, st, mid, ed);
cout << st << " " << ed << "\n";
f(n-1, mid, ed, st);
}例題
ZJ c296
題意
n 個人圍成一圈
順時針依序為 0 到 n-1
從 0 開始每數 k 個人，將其淘汰
反覆至只剩 1 人，求剩下人的編號
（細節不太一樣，這邊先無視差異）
觀察
設 n = 5, k = 3
手算結果為 3
可知數 k 人時，初淘汰者為 k-1
剩下四人圈成一圈
應該跟 n = 4, k = 3 有關？
觀察
設 n = 4, k = 3
手算結果為 0
n = 4 從 0 起算，下面 n = 5 從 3 起算
故將起點對齊
答案為 3，與手算一致
關係式
已知 n = 5 時，淘汰 1 人後從 k 開始數
n = 4 時的 0 對應到 n = 5 的 k
故 n = 4 的答案加上 k 即為 n = 5 的答案
設 f( n, k ) 為 n 人每 k 個淘汰時最後生存者
f(n, k) = (f(n-1, k) + k)\% n
歡樂練習時間
SCIST240317_Recursion
By sa072686
