SCIST240128

餘數

餘數扮演著非常重要的角色

循環

餘數有循環的性質

除以 M 的結果

理論上會落在 [0, M-1] 的範圍

餘數的循環

用除以 5 為例，數字增加時會是
0, 1, 2, 3, 4, 0, 1, 2, 3, 4, 0, …
在範圍 [0, 4] 之間無限循環

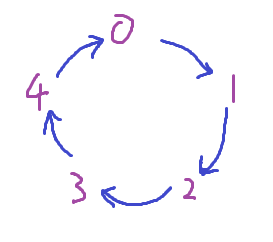
餘數的循環

同理，數字減少時會是
0, 4, 3, 2, 1, 0, 4, 3, 2, 1, 0, …
在範圍 [0, 4] 之間（逆向）無限循環

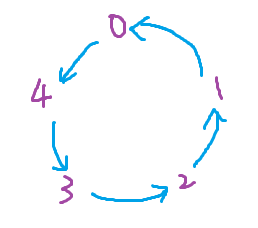
幾個重要觀察

  • 前進 M 步，餘數不變
  • 設 x + y = M 則前進 x 步和後退 y 步等價

C++ 的餘數計算

以 25 % 7 = 3 ... 4 為例
25 / 7 = 3
3 * 7 = 21
故 25 - (25 / 7) * 7 = 25 - 21 = 4

 

又，以 -25 % 7 = -3 ... -4 為例
-25 / 7 = -3
-3 * 7 = -21
故 -25 - (-25 / 7) * 7 = -25 - (-21) = -4
數學上應該是 3
逆時針前進 4 格 = 順時針前進 3 格

注意負數時餘數為負

解：C++ 中，負數除以 M 的餘數
範圍落在 [-(M-1), 0] 之間
加上 M 後為 [1, M]
再除以 M 取餘數，範圍即為 [0, M-1]


又，增加 M 相當於順時針繞完整的一圈
在圓上的位置不變，故餘數不變

應用例

面向東、南、西、北時的左轉、右轉、向後轉
可對應至左轉 = 逆時針 90 度 = 減 1 = 加 3
右轉 = 順時針 90 度 = 加 1
向後轉 = 順/逆時針 180 度 = 加 2

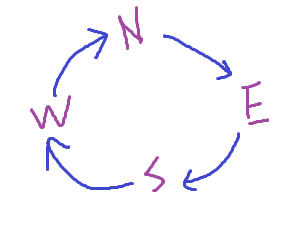
應用例

設 j = 0~3 四種值其中之一
求 j 以外的其它 3 種為何

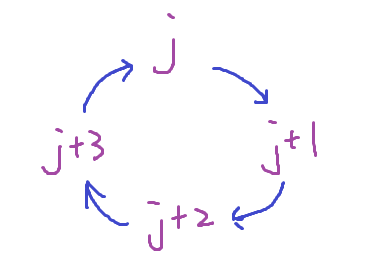
求 j 的下一種也可

應用例

給兩字串 A, B
將 A 反覆串接至和 B 一樣長
求有多少位置和 B 相異

 

例 A = KER
B = BERSERKERR
則比較
KERKERKERK
BERSERKERR
相異位置為 3

 

善用餘數就不用真的串接，想想看

限縮範圍

利用除以 M 結果為 [0, M-1] 的特性
用來限制計算結果的大小

應用例

模擬隨機丟一顆 6 面骰，點數為 1 到 6
可知範圍共 6 種不同數字
除以 6 取餘數正好會有 6 種數字 [0, 5]
加上 1 可平移至 [1, 6]

// 使用 rand() 取得隨機的一個整數
int dice = rand() % 6 + 1;

更一般化來說，目標範圍 [a, b] 可寫成

int dice = a + (rand() % (b-a+1));

餘數的計算

運算的分解

(a+b)\% M = ((a\%M) + (b\%M))\% M\\ (a-b)\% M = ((a\%M) - (b\%M)+M)\% M\\ (a\times b)\% M = ((a\%M) \times (b\%M))\% M

減法注意負數
除法不行，只有少數特殊情況可以（模逆元）

證明：將 a 代為 M*i + x
b 代為 M*j + y
試整理上式即可，可自行嘗試

應用例

求 n!（n <= 100000） 除以 1000000007
結果為何？

由於 n! 數字太大，沒有任何變數存得下
但餘數會在 int 範圍內
多確認幾組都同餘，可以判斷計算正確


1000! % M = 1 x 2 x 3 x ... x 999 x 1000 % M
= 999! x 1000 % M
= (999! % M) x (1000 % M) % M

for (i=1, ans=1; i<=n; i++)
{
	ans = ((long long)ans * i) % M;
}

延伸：奇偶性

AtCoder typical90_x

給長度 n 兩序列 A, B
每次可進行以下操作其一：

  • 選擇 i 使 A[ i ] += 1
  • 選擇 i 使 A[ i ] -= 1

求是否能在恰 k 次操作後
使 A = B

觀察

一個很顯然的條件：
A[i] 和 B[i] 的距離總和必須 <= k
但滿足以上條件後呢？

思考方向

花費 2 次操作，可在一加一減後
維持 A 不變

故 k 減去 A, B 距離和之後
剩下數字為 2 的倍數時有解
反之無解

 

證明：每次操作必改變 A 總和的奇偶
若總和奇偶不同
則總和必不可能相同
故剩餘奇數次必無解

Kattis peachpowderpolygon

給正偶數 n 邊形
將角依順時針編號 1 至 n
起始 A 在 1、B 在 2
每個角能走到相鄰角（+1或-1）
以及對角（加上 n/2）
不考慮在移動中相遇的話
A 是否有可能抓到 B
假設 A, B 皆隨機移動

進位制

人類慣用十進位，但電腦慣用二進位，所以…

進位制定義與換算

以十進位為例

每數滿 10 個進一位
故 16 代表數滿 1 次的 10 後，又數了 6
86 代表數滿 8 次的 10 後，又數了 6
256 代表數滿 25 次的 10 後，又數了 6

 

由於 25 次也超過 10 了
故記為數滿 2 次的 10 個 10，也就是 100
又數了 5 次的 10，之後又數了 6 次

十進位的定義

以數字 32767 來看
可視作數了 3276 次 10，又數 7 次
3276 可看作數了 327 次 10 後又 6 次
故為 327 次 10 個 10，和 6 次 10，…

32767 = 3276\times 10 + 7\\ = (327\times10 + 6)\times 10+7\\ = ((32\times10+7)\times10 + 6)\times 10+7\\ = (((3\times10+2)\times10+7)\times10 + 6)\times 10+7\\ = 3\times10^4+2\times10^3+7\times10^2+6\times10^1+7\times10^0

推廣至任意 b 進位

幾進位用下標方式標記，如

32767_8

表示這是 8 進位下的 32767
依定義，其表達的數字如下

3\times8^4+2\times8^3+7\times8^2+6\times8^1+7\times8^0

等同於十進位制下的 13815

b > 10 的場合

b > 10（例如常見的 16 進位）的場合
由於每位數可以出現超過 9 的數字
此時通常以 A-Z 來表達

 

例如十六進位使用 A-F 表達 10-15
故 FF = 15*16 + 15 = 255

b 進位數字轉回實際數量

可從基本定義著手，如下
（考慮 b > 10 的場合
通常採用字串形式）

// b 進位字串 number 轉換為實際代表數字放在 ans
int b;
string number;
int i, t;
int ans = 0;
for (i=number.size()-1, t=1; i>=0; i--, t*=b)
{
	int d = number[i] - '0';
    if (number[i] >= 'A' && number[i] <= 'Z')
    {
    	d = number[i] - 'A' + 10;
    }
    ans += d * t;
}

b 進位數字轉回實際數量

可從「乘以 b 加下一位」的方式著手
（考慮 b > 10 的場合
通常採用字串形式）

// b 進位字串 number 轉換為實際代表數字放在 ans
int b;
string number;
int i;
int ans = 0;
for (i=0; i<number.size(); i++)
{
	int d = number[i] - '0';
    if (number[i] >= 'A' && number[i] <= 'Z')
    {
    	d = number[i] - 'A' + 10;
    }
    ans = (ans * b) + d;
}

這形式不用倒著找個位數、不用維護 t 較方便

任意數轉換至 b 進位

從基本定義下手，以13815 轉 8 進位為例

3\times8^4+2\times8^3+7\times8^2+6\times8^1+7\times8^0

個位數是唯一不為 8 的倍數的一項
其餘每項 8 的次數均 >= 1
故 13815 % 8 = 7 即為個位數
13815 / 8 = 1726 即為個位以外的數值
即 13815 = (1726 * 8) + 7
也就是數了 1726 個 8 次後，又數了 7 次

短除法

將每次的商與餘數分寫在下、右

第一次的餘數為個位數，故由下往上看

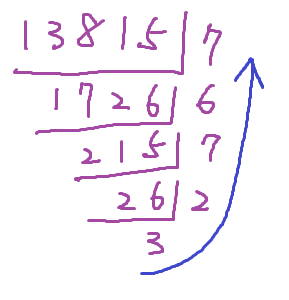
任意數轉 b 進位表達

// 將 num 轉換為 b 進位置於 str
int num;
int b;
string str;
for (; num>0; num/=b)
{
	int d = num % b;
    char c = d + '0';
    if (d >= 10)
    {
    	c = (d - 10) + 'A';
    }
    str += c;
}
// 防止一開始即為 0 的狀況
if (str.empty())
{
	str = "0";
}
// 由於最先算出的是個位數，故需反轉順序
reverse(str.begin(), str.end());

進位制只是一種表達方式

一個常見誤會是
「將不同進位制當作不同東西」
實際上只是如何表達一個
「相同的數量」

比如說上圖有幾個圓
十進位下表達為 5
二進位下為 1012
三進位則為 123
指的都是相同的「數量」

進位制只是一種表達方式

所以沒有「轉回十進位儲存」這件事
從存進變數起，就是轉二進位儲存的
實際想表達的「量」一致就行

 

是輸出時轉回十進位給人類看而已

更 general 的情況

0 到 9 的數字也只是符號
只要有可以對應 b 進位中
0 到 b-1 各自的符號
就能表達該數字

 

例如令
A 代表數字 0
O 代表數字 1
那麼 OAO 就代表「5」這個數量
用二進位表達的方式

Kattis aliennumbers

給以第一種數字系統表達的數字 n
給第一種數字系統每種數字使用的符號
給第二種數字系統每種數字使用的符號
求以第二種數字系統表達數字 n

C++ 進位制相關的語法

cin/cout

int n;
// 輸入 8 進位數字
cin >> oct >> n;
// 輸入 16 進位數字
cin >> hex >> n;
// 以 8 進位表達輸出
cout << oct << n << "\n";
// 以 16 進位表達輸出
cout << hex << n << "\n";
// 16 進位 a-z 部份以大寫表達
cout << uppercase << hex << n << "\n";

常數數字

int n;
// 二進位常數表達
n = 0b1101;
// 8 進位常數表達
n = 0204;
// 16 進位常數表達
n = 0xbeef;

應用例

給最長 100000 位數的十進位數字 n
另給整數 b < 10^9

 

求 n 是否為 b 的倍數

延伸：進位制編碼

CSES 1623

將 n 個數字分成兩堆，每個數字都要用掉
求這兩堆總和是否可能相等

思考方向

每數若不在 A 堆，就是在 B 堆
故 A, B 兩堆總和與這 n 數總和相等

 

設 n 數總和為 sum
題目可轉換為求此 n 數
每數可取可不取
求總和是否可能湊出 sum/2

窮舉

窮舉 n 數可取可不取共 2^n 種情況
但如何窮舉？

 

每數選/不選就需要一層迴圈窮舉
20 層迴圈不夠彈性、不切實際

位元窮舉

考慮將第 i 數取與不取，對應至 1/0
則 4 數取 A,C,D 不取 B
可表達為

1101

依序為 D,C,B,A

 

對於 4 數情況，可窮舉
0000 至 1111
即可看過所有可能
又 1111 等同十進位的 15
因此等同於窮舉十進位 0 到 15
再轉二進位表達，觀察每位數即可

實作示範

// n 數總和為 sum，放在 ary[0] 至 ary[n-1]
int ary[N];
int n, sum;
int i, j;
// 找到 2^n
int nn = 1;
for (i=0; i<n; i++)
{
	n *= 2;
}
// 位元窮舉
bool ans = false;
for (i=0; i<nn&&!ans; i++)
{
	// 轉二進位觀察每個位元
    int cur = 0;
    int t = i;
    for (j=0; j<n; j++, t/=2)
    {
    	// 如果代表 ary[j] 的位數為 1
    	if (t % 2 != 0)
        {
        	cur += ary[j];
        }
    }
    // 檢查總和是否符合條件
    if (cur * 2 == sum)
    {
    	ans = true;
    }
}

延伸：進位制窮舉

擲 n 次 6 面骰，求有幾種不同情況
使擲出骰子點數總和 > k

延伸：編碼為整數

例如將 bad 編碼為 27 進位的 214
則可將字串作為整數儲存或比較
也可以用作加密等用途

或者像將棋盤上的狀況轉為數字儲存、
二維陣列的座標映射回一維的儲存空間
…等都會用上

SCIST240128

By sa072686

Made with Slides.com

SCIST240128

  • 402

More from sa072686