Offline Algorithms
Contents
Mo's Algorithm
Mo's Algorithm
Let's look at the following example
You are given an array of length \(n\)
Query the distinct number of values in \([l,r]\)
\(1 \le n \le 10^5\)
This can be easily solved offline with fenwick/segment tree, but we want something easier!
Suppose we know the answer for \([l,r]\)
and we can find
the answer for
\([l,r-1],[l,r+1],[l-1,r],[l+1,r]\)
in \(O(1)\) or \(O(\log n)\)
Suppose we know the answer for \([l,r]\)
and we can find
the answer for
\([l,r-1],[l,r+1],[l-1,r],[l+1,r]\)
in \(O(1)\) or \(O(\log n)\)
1
3
2
3
2
4
5
Answer: 2
\(l = 1, r = 2\)
Action: None
1
3
2
3
2
4
5
Answer: 3
\(l = 1, r = 3\)
Action: \(r = r + 1\)
Suppose we know the answer for \([l,r]\)
and we can find
the answer for
\([l,r-1],[l,r+1],[l-1,r],[l+1,r]\)
in \(O(1)\) or \(O(\log n)\)
1
3
2
3
2
4
5
Answer: 3
\(l = 1, r = 4\)
Action: \(r = r + 1\)
Suppose we know the answer for \([l,r]\)
and we can find
the answer for
\([l,r-1],[l,r+1],[l-1,r],[l+1,r]\)
in \(O(1)\) or \(O(\log n)\)
1
3
2
3
2
4
5
Answer: 2
\(l = 2, r = 4\)
Action: \(l = l + 1\)
Suppose we know the answer for \([l,r]\)
and we can find
the answer for
\([l,r-1],[l,r+1],[l-1,r],[l+1,r]\)
in \(O(1)\) or \(O(\log n)\)
1
3
2
3
2
4
5
Answer: 2
\(l = 2, r = 3\)
Action: \(r = r - 1\)
Suppose we know the answer for \([l,r]\)
and we can find
the answer for
\([l,r-1],[l,r+1],[l-1,r],[l+1,r]\)
in \(O(1)\) or \(O(\log n)\)
1
3
2
3
2
4
5
Answer: 3
\(l = 1, r = 3\)
Action: \(l = l - 1\)
Suppose we know the answer for \([l,r]\)
and we can find
the answer for
\([l,r-1],[l,r+1],[l-1,r],[l+1,r]\)
in \(O(1)\) or \(O(\log n)\)
We can come up with the following code
vector<query> queries;
int l = 1, r = 0, ans = 0;
for(auto [ql, qr, id] : queries){
while(l < ql) del(arr[l++]); //[l+1,r]
while(r < qr) add(arr[++r]); //[l,r+1]
while(l > ql) add(arr[--l]); //[l-1,r]
while(r > qr) del(arr[r--]); //[l-1,r]
res[id] = ans;
}vector<query> queries;
int l = 1, r = 0, ans = 0;
for(auto [ql, qr, id] : queries){
while(l < ql) del(arr[l++]); //[l+1,r]
while(r < qr) add(arr[++r]); //[l,r+1]
while(l > ql) add(arr[--l]); //[l-1,r]
while(r > qr) del(arr[r--]); //[l-1,r]
res[id] = ans;
}How fast is this?
We can come up with the following code
Assume add and del work in \(O(x)\)
Each pointer will move at most \(O(n)\) per query, so the total complexity will be \(O(qnx)\)
If \(O(x) = O(1)\),then complexity is \(O(nq)\), same as bruteforce!!!
Can we do better?
Let's consider blocking
Consider \(B\) numbers as a block


We sort the queries \([l,r]\)
by the block id of \(l\)
then by \(r\)
struct query{
int l,r,id;
bool operator < (query b){
if(l/k == b.l/k) return r < b.r;
return l/k < b.l/k;
}
};Complexity analysis (let \(\lceil \frac n B \rceil\) be number of blocks)
Left pointer:
- Stay in same block: \(O(B)\)
-Move to next block: \(O(2B)\)
Left pointer will at most move \(O(qB +2B\lceil \frac{n}{B} \rceil) = O(qB+n)\)
Right pointer will move at most \(O(n)\) when left pointer stays in the same block
so it moves at most \(n \lceil \frac{n}{B} \rceil\) cells
total complexity: \(O(qB+n \lceil \frac{n}{B} \rceil)\)
To get the optimal \(B\),by AM-GM
when \(qB = n \lceil \frac{n}{B} \rceil\)
the complexity attains minimum
we have\(B = \frac{n}{\sqrt{q}}\), which gives a total complexity of \(O(n \sqrt{q})\)
The whole Mo's template
int k;
struct query{
int l,r;
bool operator < (query b){
if(l/k == b.l/k) return r/k < b.r/k;
return l/k < b.l/k;
}
};
void add(int x){
//add number
}
void del(int x){
//delete number
}
signed main(){
int n, q;
cin >> n >> q;
k = sqrt(n);
//輸入陣列
vector<query> queries;
for(int i = 0;i < q;i++){
int l,r;
cin >> l >> r;
queries.push_back({l,r,i});
}
sort(queries.begin(),queries.end());
int l = 1, r = 0, ans = 0;
for(auto [ql, qr, id] : queries){
while(l < ql) del(arr[l++]); //[l+1,r]
while(r < qr) add(arr[++r]); //[l,r+1]
while(l > ql) add(arr[--l]); //[l-1,r]
while(r > qr) del(arr[r--]); //[l-1,r]
res[id] = ans;
}
}You only need to change add, del
Practice
Mo's with modification
You are given an array of length \(n\)
and \(q\) queries, there are two types of queries:
1. query number of distinct values in \([l,r]\)
2. set \(a_i = x\)
Let's consider mo's again
We add another parameter \(t\) to \([l,r]\)
make it \([l,r,t]\)
(\(t\) represents the \(t\)th modification)
We can find the answer in \(O(1)\) for each of
\([l-1,r,t],[l+1,r,t],[l,r-1,t]\)
\([l,r+1,t],[l,r,t-1],[l,r,t+1]\)
To sort the pointers, we do it by
1. block id of l
2. block id of r
3. t
Assuming block size is \(B\)
We will analyze the time complexity
- \(l\): Move at most \(O(B)\) in same block,at most \(O(2B)\) when move to next block,total: \(O(qB)\)
- \(r\): Move at most \(O(B)\) in same block,at most \(O(2B)\) when move to next block,when \(l\) move to next block,at most \(n\) times,total: \(O(qB+n\frac{n}{B})\)
- \(t\): when \(r\) stay in same block,move at most \(q\) cells,total: \(O(q \frac{n^2}{B^2})\)
total complexity: \(O(qB+q\frac{n^2}{B^2} + \frac{n}{B})\)
\(O(qB+q\frac{n^2}{B^2} + \frac{n}{B})\)
It is hard to find the optimal B, so
we will take \(B = n^{\frac{2}{3}}\)
we get \(O(qn^{\frac 2 3} + qn^{\frac 2 3}+n^{\frac 1 3})\)
if \(n=q\),then total complexity is \(O(n^{\frac 5 3})\)
對詢問的排序
struct query{
int l, r, t, id;
bool operator < (query b){
if(l/k==b.l/k){
//l stays in same block
if(r/k==b.r/k){
//r stays in same block
return t < b.t;
}
return r/k < b.r/k;
}
return l/k < b.l/k;
}
};整份模板
int k;
struct query{
int l, r, t, id;
bool operator < (query b){
return (l/k==b.l/k ? (r/k == b.r/k ? t < b.t : r/k < b.r/k) : l/k < b.l/k);
}
} Q[N];
struct upd{
int pos,x;
} M[N];
void add(int val){
//add number
}
void del(int val){
//delete number
}
void modify(query x, upd &y){
//change number
if(x.l <= y.pos && y.pos <= x.r){
del(arr[y.pos]);
add(y.x);
}
swap(arr[y.pos],y.x);
}
signed main(){
fastio
int n, m;
cin >> n >> m;
k = pow(n,(double)2/(double)3);
for(int i = 1;i <= n;i++) cin >> arr[i];
int tid = 0, qid = 0;
for(int i = 0;i < m;i++){
char q;
cin >> q;
if(q=='Q'){
int l, r;
cin >> l >> r;
Q[qid] = {l,r,tid,qid};
qid++;
}else{
int x, val;
cin >> x >> val;
++tid;
M[tid] = {x,val};
}
}
sort(Q,Q+qid);
int l = 1, r = 0, t = 0;
for(int i = 0;i < qid;i++){
auto q = Q[i];
while(l < q.l) del(arr[l++]);
while(l > q.l) add(arr[--l]);
while(r < q.r) add(arr[++r]);
while(r > q.r) del(arr[r--]);
while(t < q.t) modify(Q[i],M[++t]);
while(t > q.t) modify(Q[i],M[t--]);
ans[q.id] = tmp;
}
for(int i = 0;i < qid;i++) cout << ans[i] << "\n";
}Practice
回滾莫隊
(Rollback Mo's Algorithm)
給你一個 \(n\) 項的陣列,有 \(q\) 次詢問
每次詢問區間 \([l,r]\) 當中 \(\max(cnt_x \times x)\) 的值
既然我們一直在講莫隊,那我們就來用莫隊ㄅ
不過你會發現
在進行 加入數字 的操作時
我們可以很輕易的 \(O(1)\) 解決
但刪除數字呢?
void add(int val){
cnt[val]++;
tmp = max(cnt[val]*val,tmp);
}
void del(int val){
//How???
}Add 和 Del
刪除很難怎麼辦??
那如果我們會 回復上一次操作 呢?
stack<pair<int,int>> stk;
void add(int val){
stk.push({val,res});
cnt[val]++;
res = max(cnt[val]*val,res);
}
void rollback(){
assert(!stk.empty());
auto [val, tmp] = stk.top(); stk.pop();
cnt[val]--;
res = tmp;
}
Add 和 Rollback!
如果要處理 \([l,r]\) 的詢問怎麼做?
\(l,r\) 同塊? 直接暴力做完,複雜度 \(O(B)\)
不同塊?
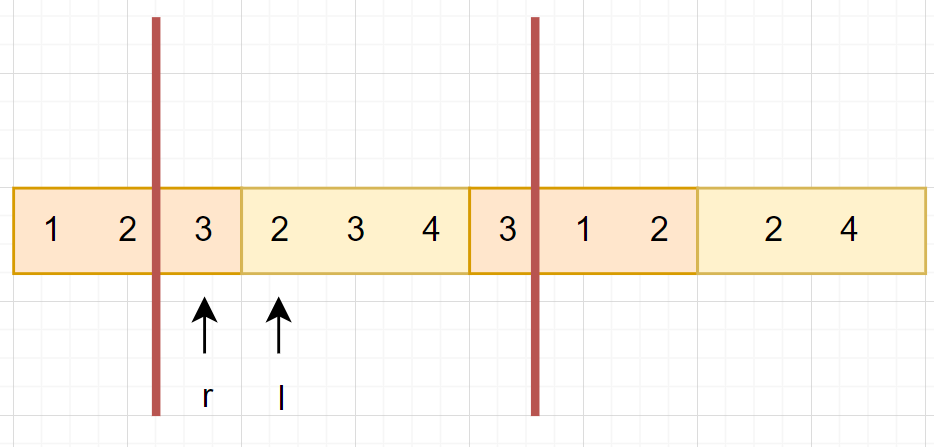
我們將 \(r\) 放置在詢問左界的塊的最後
把 \(l\) 放置在詢問左界的塊 + 1 的前面
會發現這樣在移動的時候,只會有加值的操作

1. 先把 \(r\) 往右延伸區間
2. 把 \(l\) 往前延伸區間
3. 回朔 \(l\)
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
先移動 \(r\)
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
先移動 \(r\)
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
先移動 \(r\)
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
再移動 \(l\)
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
做完紅色的詢問了
Rollback!
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
做完紅色的詢問了
Rollback!
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
做完紅色的詢問了
Rollback!
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
下一個詢問
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
下一個詢問
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
下一個詢問
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
做完了,回滾!
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
做完了,回滾!
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
不同塊了,怎麼辦?
rollback \(r\)!
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
不同塊了,怎麼辦?
rollback \(r\)!
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
不同塊了,怎麼辦?
rollback \(r\)!
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
不同塊了,怎麼辦?
rollback \(r\)!
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
不同塊了,怎麼辦?
rollback \(r\)!
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
把 \(l,r\) 直接移到他們該去的地方
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
把 \(l,r\) 直接移到他們該去的地方
回滾莫隊就是這樣!
我們來分析時間複雜度
複雜度分析:
\(l\): 每次詢問完和 rollback 時最多移動 \(O(2B)\)
換塊最多移動 \(O(B)\)
\(r\): 在 \(l\) 同塊時,最多移動 \(O(n)\)
總共最多移動 \(O(nB)\)
\(l,r\) 同塊時,最多移動 \(O(B)\)
時間複雜度: \(O(qB+n\frac{n}{B})\)
(取 \(B = \frac{n}{\sqrt{q}}\) 時,有 \(O(n \sqrt{q})\))
回滾莫隊模板
struct query{
int l,r,id;
bool operator < (query b){
return (l/k==b.l/k ? r < b.r : l/k < b.l/k);
}
};
void add(int val){
//加入數字
}
void rollback(){
//Rollback
}
signed main(){
fastio
int n,q;
cin >> n >> q;
k = sqrt(n);
for(int i = 1;i <= n;i++){
cin >> arr[i];
}
vector<query> queries;
int ans[q];
for(int i = 0;i < q;i++){
int l,r;
cin >> l >> r;
if(l/k == r/k){
for(int j = l;j <= r;j++){
add(arr[j]);
}
ans[i] = res;
for(int j = l;j <= r;j++){
rollback();
}
}
queries.push_back({l,r,i});
}
sort(queries.begin(),queries.end());
int lst = -1, l = 1, r = 0;
for(auto [ql,qr,id] : queries){
if(ql/k == qr/k) continue;
if(ql/k!=lst){
while(!stk.empty()) rollback();
l = (ql/k+1)*k, r = (ql/k+1)*k-1;
lst = ql/k;
}
while(r < qr) add(arr[++r]);
while(l > ql) add(arr[--l]);
ans[id] = res;
while(l < (ql/k+1)*k) rollback(), l++;
}
for(int i = 0;i < q;i++) cout << ans[i] << "\n";
}練習題
CF EDU DSU - Number of Connect Components on Segments
區間 Mex (我不知道哪裡有)
Codeforces 840D - Destiny (有分治或隨機做法)
Copy of 離線演算法
By sam571128
Copy of 離線演算法
- 23



