Greedy
UMD CP Club Fall 2023


Classical Problems

There are \(n\) tasks, each of them has deadline \(d_i\), and each of them took you \(t_i\) time to finish. Suppose the finish time of each task is \(f_i\). Try to minimize
$$\sum_{i=1}^n (d_i - f_i)$$
Constraint: \(1 \le n \le 10^5\)

What would be the strategy you want to use?

An interesting strategy might be to "Do the one whose deadline is earlier"

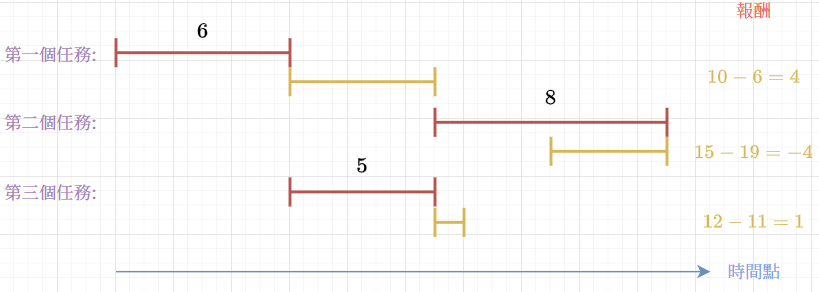
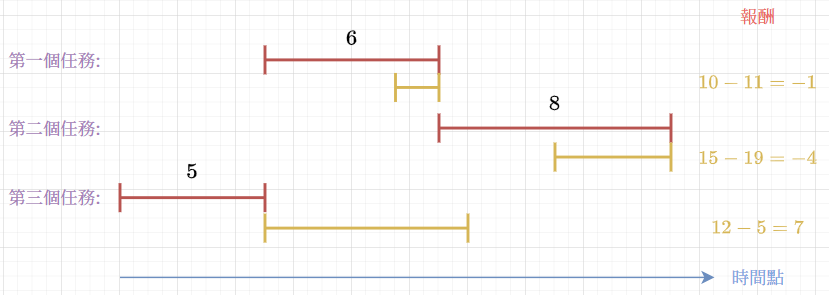
Consider the sample of the problem

Taking shorter duration is better!

#include <bits/stdc++.h>
#define int long long
#define fastio ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
using namespace std;
const int N = 2e5+5;
pair<int,int> arr[N];
signed main(){
fastio
int n;
cin >> n;
for(int i = 0;i < n;i++){
cin >> arr[i].first >> arr[i].second;
}
sort(arr,arr+n);
int nowtime = 0;
int ans = 0;
for(int i = 0;i < n;i++){
nowtime += arr[i].first;
ans += arr[i].second - nowtime;
}
cout << ans << "\n";
}
You are given \(n\) strings \(s_1, s_2, \cdots, s_n\). Find the lexicographically smallest concatenation of the strings
Constraint: \(n \le 5 \times 10^4, |s_i| \le 50\)

Sort by the following comparator:
\(a + b < b + a\)

sort(v.begin(),v.end(),[&](auto a, auto b){
return a+b < b+a;
});
In a movie festival \(n\) movies will be shown. You know the starting and ending time of each movie \([l_i, r_i]\). What is the maximum number of movies you can watch entirely?
\(1 \le n \le 10^5\)

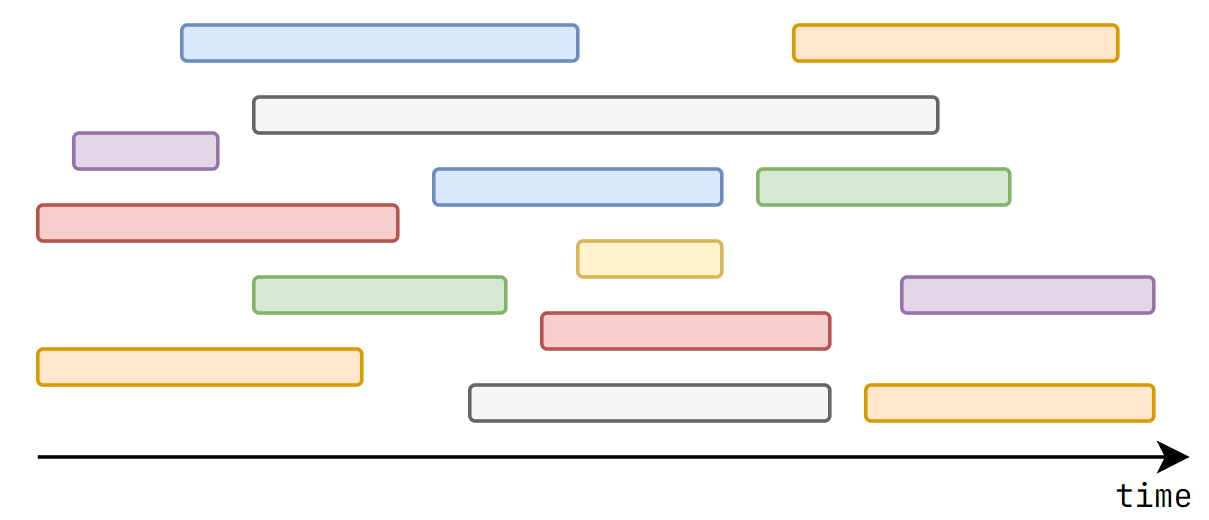

Sort by the right interval, and it works!

#include <bits/stdc++.h>
#define fastio ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
using namespace std;
int main(){
fastio
int n;
cin >> n;
vector<pair<int,int>> v;
for(int i = 0;i < n;i++){
int l,r;
cin >> l >> r;
v.push_back({l,r});
}
sort(v.begin(),v.end(),[&](pair<int,int> a, pair<int,int> b){
return a.second < b.second;
});
int now = 0, ans = 0;
for(auto x : v){
if(x.first >= now){
ans++, now = x.second;
}
}
cout << ans << "\n";
}
Undo Greedy

We talked about this few weeks ago



Other cool problems

Other cool problems



UMD CP Club - Greedy
By sam571128
UMD CP Club - Greedy
- 272



