Basic Data Structures

UMD CP Club Fall 2023 - Meeting 2

C++ STL Data Structures

We will use my old slide for this

C++ Policy Based Data Structures (PBDS)

Policy Based Data Structures

In C++, there are some data structures that are very powerful included in

__gnu_pbds

Policy Based Data Structures

There are some data structures we sometimes use from this library

  1. An ordered_set that allows querying the kth largest element
  2. A hash table that is faster than unordered_map
  3. A priority_queue that allows \(O(1)\) merge
  4. A persistent trie that can do some operations like treap

All of these are really powerful data structures

Policy Based Data Structures - Tree

The first data structure we will talk about is the BST

#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
using namespace __gnu_pbds;

We will need to include the header file

you can also use <bits/extc++.h> to include everything

Policy Based Data Structures - Tree

To initialize the data structure, we will need to do

typedef tree<
int,
null_type,
less<int>,
rb_tree_tag,
tree_order_statistics_node_update>
ordered_set;

We typedef it because it's too long

Policy Based Data Structures - Tree

The data structure has almost the same usage as std::set

but what we really like about this data structure is to do these

ordered_set st;
st.insert(10);
st.insert(5);
st.insert(8);
cout << *st.find_by_order(1) << '\n'; // find the kth largest element
cout << st.order_of_key(1) << '\n'; // find the number of elements < x
cout << st.order_of_key(9) << '\n';

Policy Based Data Structures - Tree

Example Problem:  CSES - Josephus Problem II

Policy Based Data Structures - Hash Table

We can initialize the hash table by doing

gp_hash_table<key, value> ht;

All usage are the same as unordered_map

You can find more informations in this cf blog

Disjoint Set Union (DSU)

We want a data structure that maintains multiple disjoint sets (or a graph)

slide

Prefix Sum & Difference Array

slide

Fenwick Tree
(aka Binary Indexed Tree, BIT)

As we just talked about, we can use prefix sum to answer range queries

What if now, the elements in the array can change?

CSES - Dynamic Range Sum Queries

You are given an array \(a_1, a_2, \cdots, a_n\). There will be \(q\) queries. There are two types of queries

  1. update the value of \(a_i\) to \(x\)
  2. output the sum of values in \([l,r]\)
  • \(1 \le n \le 10^6\)
  • \(1 \le q \le 10^6\)

CSES - Dynamic Range Sum Queries

Directly doing this by bruteforcing, we can do the queries in \(O(1)/O(n)\)

Doing this with prefix sums, we can do the queries in \(O(n)/O(1)\)

How can we make this faster?

We will introduce a data structure that can do the following things:

  1. add \(x\) to a \(a_i\)
  2. query the prefix sum \([1, i]\)

Both in \(O(\log n)\)

Prerequisite

You are given an integer \(x\) (int x / long long x)

How can we find the least significant bit (lowbit) of \(x\)?

For example

\(5 = (101)_2 \implies \text{lowbit}(5) = 1\)

\(10 = (1010)_2 \implies \text{lowbit}(10) = 2\)

Prerequisite (Recall two's complement from 216)

In computers, signed integers are stored with two's complement

A \(k\)-bit integer stores as binary form \(b_{k-1}b_{k-2}\ldots b_0\) has value

b_{k-1} (-2^{k-1}) + b_{k-2} 2^{k-2} + \cdots + b_0 2^0

Prerequisite (Recall two's complement from 216)

We can show that \(\text{lowbit}(x) = \texttt{x \& -x}\)

and this can be done in \(O(1)\)

Fenwick Tree

Now, we will define an array \(\texttt{bit[i]} = \text{sum}(i-\text{lowbit}(i) + 1, i)\)

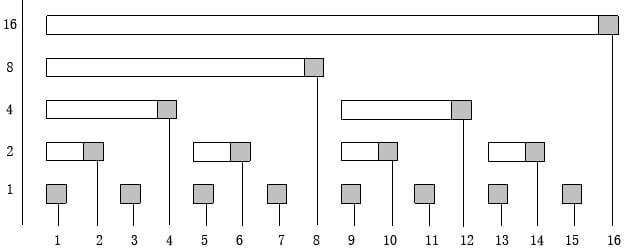
Fenwick Tree

The following code handles the query (the prefix sum part)

int query(int pos) {
    int ans = 0;
    while (pos < MAXN) {
        ans += bit[pos];
        pos -= pos & -pos;
    }
    return ans;
}

Fenwick Tree

The following code handles the update

int update(int pos, int val) {
    while (pos < MAXN) {
        bit[pos] += val;
        pos += pos & -pos;
    }
    return ans;
}

Fenwick Tree

Both of these operations can be written ~4 lines of code

Let's now use it to solve some problems!

Fenwick Tree

Counting inversions

Longest Increasing Subsequence

CSES - Projects

Segment Tree

We will do this next week (or some day)

UMD CP Club - Basic Data Structures

By sam571128

Made with Slides.com

UMD CP Club - Basic Data Structures

  • 85

More from sam571128