Basic Techniques
UMD CP Club Summer CP Week 3
Greedy Algorithms
Let's look at a simple task
Suppose you have unlimited number of coins with values \(\{\$1,\$5,\$10,\$50,\$100\}\) and you want to buy a phone that costs \(\$567\). What is the minimum number of coins you have to take to pay exactly \(\$567\)?
A Simple Task
You take \(5 \times \$100\), \(1 \times \$50\), \(1 \times \$10\), \(1 \times \$5\), and \(2 \times \$1\).
This is also the minimum number of coins required
Suppose you have unlimited number of coins with values \(\{\$1,\$5,\$10,\$50,\$100\}\) and you want to buy a phone that costs \(\$567\). What is the minimum number of coins you have to take to pay exactly \(\$567\)?
A Simple Task
If you think that is intuitive, then what we just did is called a "Greedy Algorithm"
The Greedy thought is that
Always taking the maximum value\(\implies\) minimum number of coins
So what exactly is Greedy Algorithm
Last week, we learned about searching
So let's write a code that searches all possibilities
int values[] = {1, 5, 10, 50, 100};
int search(int x){
if(x < 0) return 1e9;
if(x == 0) return 0;
int mn = 1e9;
for(int i = 0; i < 5; i++){
mn = min(mn, search(x - values[i]) + 1);
}
return mn;
}code for coins problem
So what exactly is Greedy Algorithm
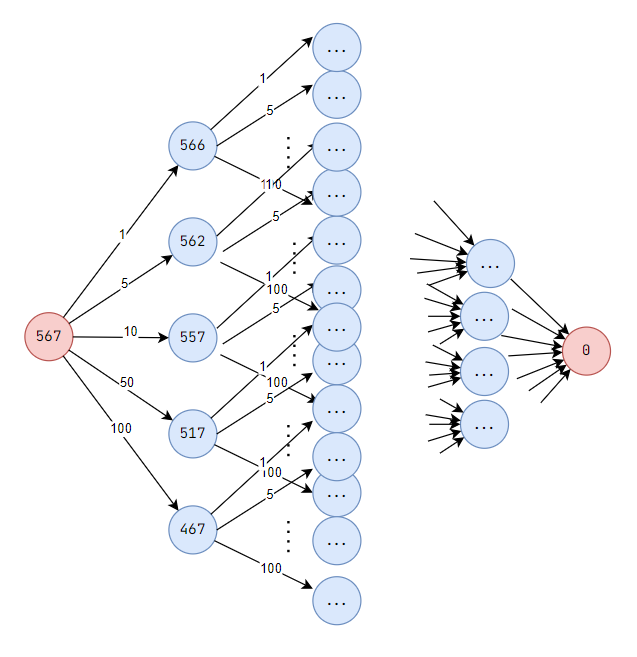
So what exactly is Greedy Algorithm
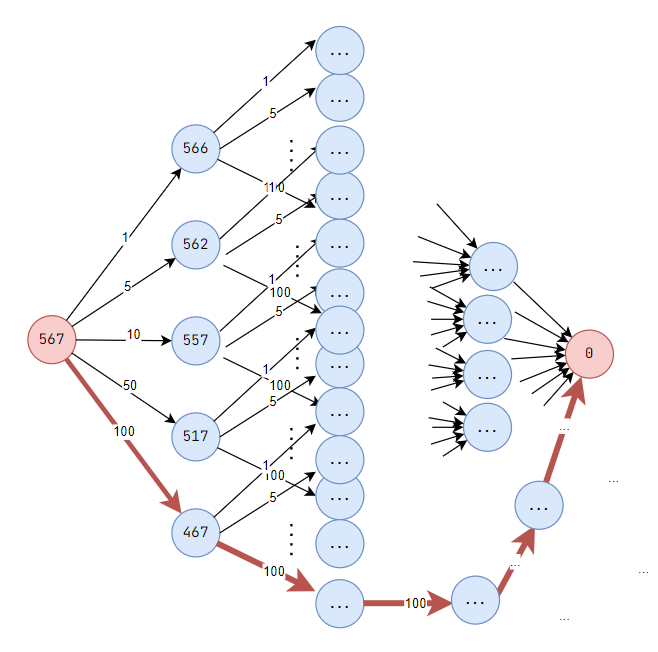
So what exactly is Greedy Algorithm
So, greedy algorithm is to find a way to solve an optimization problem faster!
Is Greedy always correct?
A different example
Suppose you have unlimited number of coins with values \(\{\$1,\$5, \$8\}\) and you want to buy something that costs \(\$x\). What is the minimum number of coins you have to take to pay exactly \(\$x\)?
What if \(x = 15\)?
Greedy Can Sometimes be Incorrect!
We have to prove the correctness of our algorithm!
Let's prove "Coin Change" problem
Coin Change
Suppose you have unlimited number of coins with \(n\) different denominations, each with \(c_1, c_2, \cdots, c_n\). You want to buy a product with price \(x\). Find the minimum number of coins required to pay exactly \(x\)
- \(1 \le n \le 10^6\)
- \(c_i < c_{i+1} \text{ and } c_i \mid c_{i+1}\)
Text
To start with, let's think about why greedy works?
Coin Change
Coin Change
Text
To start with, let's think about why greedy works?
Coin Change
Text
To start with, let's think about why greedy works?
If the denominations includes \(\$1\) and \(\$5\)
and you have 5 \(\$1\). What would you do?
Convert them into 1 \(\$5\)!
Text
Coin Change
Claim 1. In the optimal solution, we won't take more than \(\frac{c_{i+1}}{c_i}\) coins with denomination \(c_i\)
Coin Change
Text
Proof.
Suppose you have \(\ge \frac{c_{i+1}}{c_i}\) coins with denomination \(c_i\). We can convert \(\frac{c_{i+1}}{c_i}\) (\(> 1\)) of the coins into one \(c_i\) coin, and get a better result.
Claim 1. In the optimal solution, we won't take more than \(\frac{c_{i+1}}{c_i}\) coins with denomination \(c_i\)
Text
Claim 2. In the optimal solution, if \(c_i \le x < c_{i+1}\). Then \(c_i\) must be taken.
Coin Change
Text
Proof (Part of).
(\frac{c_2}{c_1}-1)c_1 + (\frac{c_3}{c_2}-1)c_2 + \cdots + (\frac{c_i}{c_{i-1}}-1)c_i \\= (c_2 - c_1) + (c_3 - c_2) + \cdots + (c_i - c_{i-1}) =
c_i - c_1 < c_i
Claim 2. In the optimal solution, if \(c_i \le x < c_{i+1}\). Then \(c_i\) must be taken.
Coin Change
Coin Change
Text
From these two claims, you can show that the greedy algorithm is actually optimal
Text
CSES - Movie Festival (Interval Scheduling)
There are \(n\) movies, each starts at \(l_i\) and ends at \(r_i\).
You want to find the maximum number of movies that you can watch completely
- \(1 \le n \le 10^6\)
Text
CSES - Movie Festival (Interval Scheduling)
There are \(n\) movies, each starts at \(l_i\) and ends at \(r_i\).
You want to find the maximum number of movies that you can watch completely
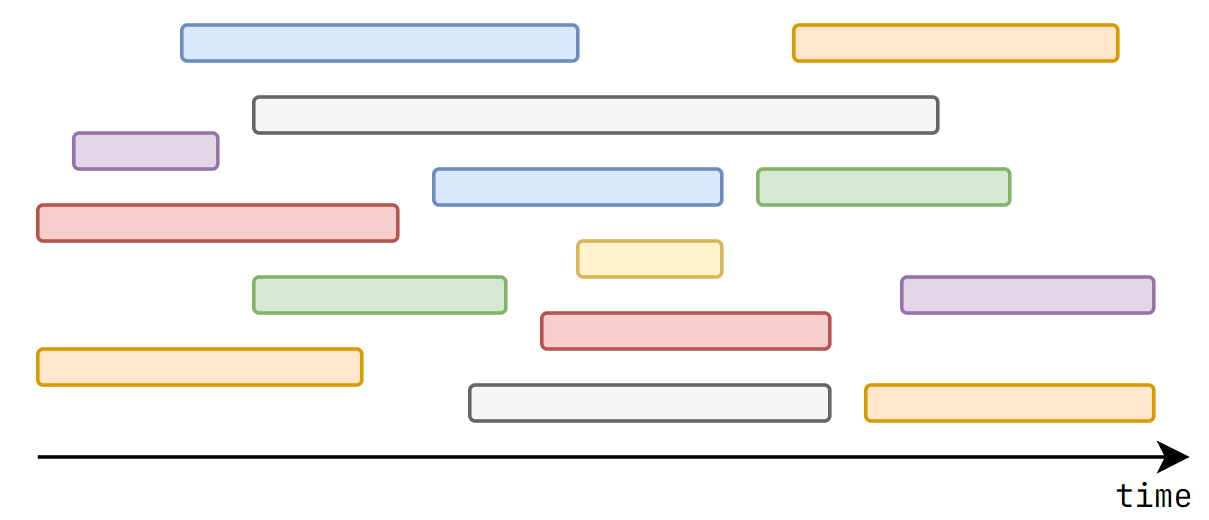
Text
CSES - Movie Festival (Interval Scheduling)
What if we start watching movies with the earliest starting time?
Text
CSES - Movie Festival (Interval Scheduling)
What if we start watching movies with the earliest starting time?
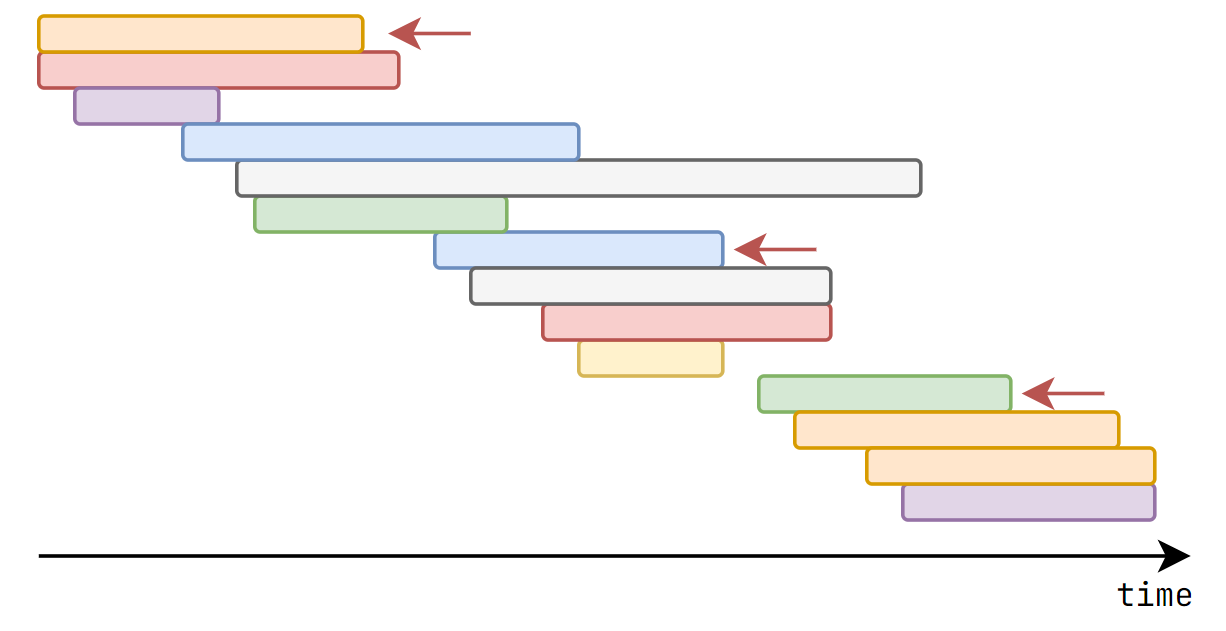
Text
CSES - Movie Festival (Interval Scheduling)
The optimal solution is actually to watch movie with earliest ending time!
Text
CSES - Movie Festival (Interval Scheduling)
The optimal solution is actually to watch movie with earliest ending time!
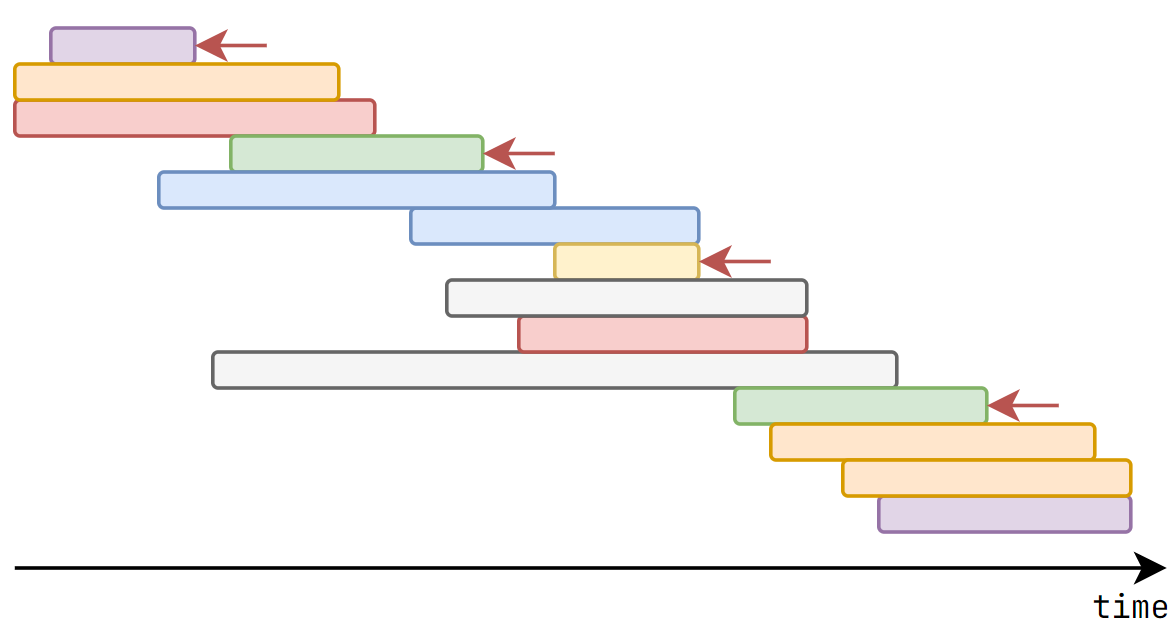
CSES - Movie Festival (Interval Scheduling)
We will prove that this greedy method is correct!
CSES - Movie Festival (Interval Scheduling)
Claim. Sort the intervals by \(r_i\) and watch the movies in order will give optimal answer
CSES - Movie Festival (Interval Scheduling)
Claim. Sort the intervals by \(r_i\) and watch the movies in order will give optimal answer
Proof.
Let the movies watched by greedy algorithms be \(\{a_1, a_2, \cdots, a_n\}\), and \(\{b_1, b_2, \cdots, b_m\}\) be an optimal choice
in which all \(a_i, b_i\) are indices, and \(r_{a_i} \le r_{a_{i+1}}\), \(r_{b_i} \le r_{b_{i+1}}\)
CSES - Movie Festival (Interval Scheduling)
Claim. Sort the intervals by \(r_i\) and watch the movies in order will give optimal answer
Proof.
Let the movies watched by greedy algorithms be \(\{a_1, a_2, \cdots, a_n\}\), and \(\{b_1, b_2, \cdots, b_m\}\) be an optimal choice
in which all \(a_i, b_i\) are indices, and \(r_{a_i} \le r_{a_{i+1}}\), \(r_{b_i} \le r_{b_{i+1}}\)
CSES - Movie Festival (Interval Scheduling)
Proof (Continued).
We claim that \(r_{a_i} \le r_{b_i}\) for all \(1 \le i \le \min(m,n)\)
we will prove this by induction on \(i\)
Base Case: When \(i = 1\), then the induction hypothesis holds by the design of greedy algorithm
Inductive Step: Suppose the hypothesis holds for all \(k \le i\). Then since \(r_{b_{i-1}} \le l_{b_i}\), we get \(r_{a_{i-1}} \le l_{b_i}\). Therefore, greedy algorithm can also take interval \(b_i\). Hence, \(r_{a_i} \le r_{b_i}\)
CSES - Movie Festival (Interval Scheduling)
Proof (Continued).
We proved that \(r_{a_i} \le r_{b_i}\) for all \(1 \le i \le \min(m,n)\)
CSES - Movie Festival (Interval Scheduling)
Proof (Continued).
We proved that \(r_{a_i} \le r_{b_i}\) for all \(1 \le i \le \min(m,n)\)
Now suppose \(n < m\) (greedy is worse than optimal solution), then it means that the optimal soluton takes at least one interval more than the greedy solution.
CSES - Movie Festival (Interval Scheduling)
Proof (Continued).
We proved that \(r_{a_i} \le r_{b_i}\) for all \(1 \le i \le \min(m,n)\)
Now suppose \(n < m\) (greedy is worse than optimal solution), then it means that the optimal soluton takes at least one interval more than the greedy solution.
We have \(r_{b_n} \le l_{b_{n+1}}\), and therefore \(r_{a_n} \le l_{b_{n+1}}\). This means greedy can also take interval \(b_{n+1}\), this is a contradiction.
How to solve Greedy Problems
- Come up with a greedy thought that might work
- You have to make sure it's correct
- Prove it! (Try to do this when solving problems)
- Prove by AC (It is fine to do this in contests)
Ways to prove Greedy Algorithm
- Let \(S\) be the answer from Greedy, and \(S'\) be the an optimal solution
- Suppose \(S\) is not optimal, show contradiction
Exchange Argument
We claim that the queue sorted this way is optimal
// Let v[i] = {a_i, b_i}
sort(v.begin(),v.end(), [](auto a, auto b){
return a.second * (a.second-2) + a.first * (a.first + 5) \
< b.second * (b.second-2) + b.first * (b.first + 5);
});In this type of greedy, try to think about what would happen when you swap two people
Suppose the sequence is now \(\{c_1, c_2, \cdots, c_n\}\)
Then the sum of impatience will be
\sum_{i=1}^n \sum_{j=i+1}^n \left (b_{c_i}(b_{c_i}-2) - a_{c_j}(a_{c_j}+5) \right )
What would happen if we swap \(c_i, c_j\)?
What would happen if we swap \(c_i, c_j \ (i < j)\)?
\Delta_{cost}
= \left (-\sum_{i < k < j} b_{c_i}(b_{c_i}-2)\right) + \left (\sum_{i < k < j} b_{c_j}(b_{c_j}-2)\right) + \left (j-i+1) (a_{c_j}(a_{c_j}+5) - a_{c_i}(a_{c_i}+5)\right) \\
= (j-i+1)(a_{c_j}(a_{c_j}+5) - a_{c_i}(a_{c_i}+5) - b_{c_i}(b_{c_i}-2) + b_{c_j}(b_{c_j}-2))
So if there are two elements where
\(a_{c_i}(a_{c_i}+5) + b_{c_i}(b_{c_i}-2) > a_{c_j}(a_{c_j}+5) + b_{c_j}(b_{c_j}-2) \)
Swap them gives smaller costs!
This type of greedy is called Exchange Argument
We can prove that sorting (swaping) would give optimal solution
Undo Greedy
4
-4
1
-3
1
-3
Initially your HP is \(0\), you have to start from left
Each potion will add \(a_i\) to your HP
Your HP need to be \(\ge 0\) at all time
Find the maximum number of potions you can drink
4
-4
1
-3
1
-3
Claim. It is always best to drink \(a_i \ge 0\)
Proof. Trivial
4
-4
1
-3
1
-3
What about \(a_i < 0\)?
4
-4
1
-3
1
-3
There are two cases for \(a_i < 0\)
- \(hp > 0\)
- \(hp \le 0\)
If it is first case, just drink it.
4
-4
1
-3
1
-3
If after drinking \(a_i\), your hp is now below \(0\)
Think about if it is possible to undrink some negative potion
4
-4
1
-3
1
-3
Red mean we do not drink
Green means we drink it
\text{health} = 0
4
-4
1
-3
1
-3
Red mean we do not drink
Green means we drink it
\text{health} = 4
4
-4
1
-3
1
-3
Red mean we do not drink
Green means we drink it
\text{health} = 0
4
-4
1
-3
1
-3
Red mean we do not drink
Green means we drink it
\text{health} = 1
4
-4
1
-3
1
-3
Red mean we do not drink
Green means we drink it
\text{health} = 1
Should we drink \(-3\) here?
The answer is Yes!
We undrink \(-4\) and drink \(-3\)!
4
-4
1
-3
1
-3
Red mean we do not drink
Green means we drink it
\text{health} = 2
4
-4
1
-3
1
-3
Red mean we do not drink
Green means we drink it
\text{health} = 3
4
-4
1
-3
1
-3
Red mean we do not drink
Green means we drink it
\text{health} = 0
This is the final code of this problem
int n;
cin >> n;
int sum = 0;
priority_queue<int,vector<int>,greater<>> pq;
for(int i = 0;i < n;i++){
int x;
cin >> x;
pq.push(x);
sum += x;
while(sum < 0){
sum -= pq.top();
pq.pop();
}
}
cout << pq.size() << '\n';Greedy requires some experiences
So it is actually normal if you don't understand
Just practice more and you will get it!
Modular Arithmetic
In Competitive Programming Problems (Usually Math or DP)
Since the answer could be large, output the answer modulo \(10^9+7\)
Is a very common sentence that you will see in CP problems
We need modular arithmetic to prevent large numbers / overflow
In math, we denote
x \equiv y \pmod m
if \(x \bmod m = y \bmod m\)
and \(0 \le (x \bmod m) < m\)
Under modulo, these three operations will hold
(a \bmod m) + (b \bmod m) \equiv a + b \pmod m
(a \bmod m) - (b \bmod m) \equiv a - b \pmod m
(a \bmod m) \times (b \bmod m) \equiv a \times b \pmod m
This can be easily shown with Division Algorithm
However, how can we do division?
\frac{a \bmod m}{b \bmod m} \not \equiv \frac{a}{b} \pmod m
To do division under modulo, we need modular inverse!
Definition.
\(b\) is the modular inverse of \(a\) under modulo \(m\) iff
\(ab \equiv 1 \pmod m\)
We denote \(b\) as \(a^{-1}\)
We can do division under modulo where
ab^{-1}
means \(a\) divided by \(b\)
There are three ways to find modular inverse in CP
- Fermat's Little Theorem
- A Recurrence that Works
- Extended Euclidean Algorithm
We will only talk about Fermat's Little Theorem
and focus on the case when \(m\) is a prime
Binary Exponentiation
Now, suppose we want to find the value of
\(a^n\)
How can you do this?
Binary Exponentiation
a^n = \underbrace{a \times a \times \cdots \times a}_{n \text{ times}}
This can be done in \(O(n)\)
\(n \le 10^9\)
Binary Exponentiation
Think about it, what would you do when you want to calculate
3^8
without a calculator
Binary Exponentiation
3^8 = 3^4 \times 3^4
Binary Exponentiation
3^8 = 3^4 \times 3^4 \\
3^4 = 3^2 \times 3^2 \\
3^2 = 3^1 \times 3^1
Binary Exponentiation
3^8 = 3^4 \times 3^4 \\
3^4 = 3^2 \times 3^2 \\
3^2 = 3^1 \times 3^1
Can you do same thing with arbitrary n?
Binary Exponentiation
a^n
Binary Exponentiation
a^n = a^{\lfloor \frac{a}{2} \rfloor} \times a^{\lfloor \frac{a}{2} \rfloor} \times a^{(n \bmod 2)}
We can now do this in
\(T(n) = T(\frac{1}{2} n) + O(1) \implies O(\log n)\)
Binary Exponentiation
int fastpow(int a, int n){
if(n == 0) return 1;
int tmp = fastpow(a, n/2);
return tmp * tmp * (n % 2 ? a : 1);
}Recursive binary exponentiation
Binary Exponentiation
There is also another way
Binary Exponentiation
a^{15} = a^{(1111)_2} = a^8 \times a^4 \times a^2 \times a
If you convert \(n\) into binary
then you also only need to do \(O(\log n)\)!
Binary Exponentiation
int fastpow(int a, int n){
int res = 1;
while(n){
if(n % 2 == 1) res *= a;
a = a * a;
n >>= 1;
}
return res;
}Iterative binary exponentiation
Fermat's Little Theorem
Fermat's Little Theorem
From number theory, we know that if \(p\) is prime then
a^p \equiv a \pmod p
By the Fermat's Little Theorem
Fermat's Little Theorem
a^p \equiv a \pmod p
multiplying \(a^{-2}\) on both sides, we get
a^{p-2} \equiv a^{-1} \pmod p
which is the modular inverse!
Fermat's Little Theorem
int fastpow(int a, int n, int mod);
int inv(int a, int p){
return fastpow(a, p-2, p);
}code for modular inverse in \(O(\log n)\)
Be careful!
In C++, \(a \% b\) is defined as \(a - b \lfloor \frac{a}{b} \rfloor\)
This means it could possibly give negative results (e.g. -4 % 3 = -1)
You will have to convert it back to \([1,m]\)
Small Practice (Use C++)
Evaluate the following values with C++
- \((100000 \times 99999) \bmod 13\)
- \(2^{100} \bmod 10^9+7\)
- \(((−4) × 1234567890) \bmod 998244353\)
- \(100\)th fibonacci number \(\bmod 10^9+7\)
Small Practice (Use C++)
Evaluate the following values with C++
- \((100000 \times 99999) \bmod 13\)
- \(2^{100} \bmod 10^9+7\)
- \(((−4) × 1234567890) \bmod 998244353\)
- \(100\)th fibonacci number \(\bmod 10^9+7\)
Answer:
1297637128552950205782204094
Prefix Sum & Difference Array
You are given an array \(a_1, a_2, \cdots, a_n\). There will be \(q\) queries. For each query \([l,r]\), output the sum of values in \([l,r]\).
\sum_{i=l}^r a_i
- \(1 \le n \le 10^6\)
- \(1 \le q \le 10^6\)
Naive Solution
int sum = 0;
for(int i = l; i <= r; i++){
sum += arr[i];
}
cout << sum << "\n";This is too slow! \(O(nq)\)
Let \(pref[i] = \sum_{j = 1}^i a_j\), which is the sum from \([1,i]\)
Then \([l,r]\) can be calculated by \([1,r]\) - \([1,l-1]\)
We can precompute \(pref\) in \(O(n)\), then each query can be answered in \(O(1)\)!
int pref[n+1] = {};
for(int i = 1; i <= n; i++){
pref[i] = arr[i];
pref[i] += pref[i-1];
}
int q;
cin >> q;
while(q--){
int l, r;
cin >> l >> r;
cout << pref[r] - pref[l-1] << "\n";
}The array \(pref[i]\) is called the prefix sum of \(a\)
When you need multiple queries of a range, finding prefix sum can do it in \(O(1)\)
You are given an array \(a_1, a_2, \cdots, a_n\).
There will be \(q\) operations. For each operation, add \(v\) to \([l,r]\).
After all the operations, output the final array
- \(1 \le n \le 10^7\)
- \(1 \le q \le 2 \times 10^5\)
Think about what would not change when we add values to a range?
Think about what would not change when we add values to a range?
1, \ 2, \ 3, \ 4, \ 5, \ 6, \ 7, \ 8
+1
Think about what would not change when we add values to a range?
1, \ 2, \ 3, \ 4, \ 5, \ 6, \ 7, \ 8
+1
\Downarrow
1, \ 2, \ 4, \ 5, \ 6, \ 7, \ 8, \ 8
The difference between \(a_3, a_4, a_5, a_6, a_7\) did not change!
Let's declare another array \(b_i = a_i - a_{i-1}\), and we call \(b_i\) the difference array of \(a\)
Then the prefix sum of \(b\), \(\sum_{k=1}^i b_i = a_1 + (a_2 - a_1) + \cdots + (a_i - a_{i-1}) = a_i\)
Let's see what this can help us in this problem
a = 1, \ 2, \ 3, \ 4, \ 5, \ 6, \ 7, \ 8
+1
b = 1, \ 1, \ 1, \ 1, \ 1, \ 1, \ 1, \ 1
\Downarrow
a = 1, \ 2, \ 4, \ 5, \ 6, \ 7, \ 8, \ 8
b = 1, \ 1, \ 2, \ 1, \ 1, \ 1, \ 1, \ 0
We add \(1\) to \([3,7]\), then the result shows
\(b_l := b_l + v, b_{r+1} := b_{r+1} - v\)
Therefore, for each operation, we only need to modify two elements from \(b\)
This can be done in \(O(1)\)
To find \(a\), just do prefix sum to \(b\) after all operations!
int b[n+1];
for(int i = 1; i <= n; i++){
b[i] = a[i] - a[i-1];
}
int q;
cin >> q;
while(q--){
int l, r, v;
cin >> l >> r >> v;
b[l] += v, b[r+1] -= v;
}
for(int i = 1; i <= n; i++){
b[i] += b[i-1];
}
//b is the original array after opeartionsO(n + q)
Actually, prefix sum and difference array are inverse operations
Actually, prefix sum and difference array are inverse operations
You can also find prefix xor, prefix product to do similar things
2D Prefix Sums
You are given an \(n \times n\) grid. Each cell is either empty or contains a tree.
There will be \(q\) queries. For each query, output how many trees are there in the rectangle with top left corner \((a,b)\) and bottom right corner \((c,d)\).
- \(1 \le n \le 2000\)
- \(1 \le q \le 10^6\)
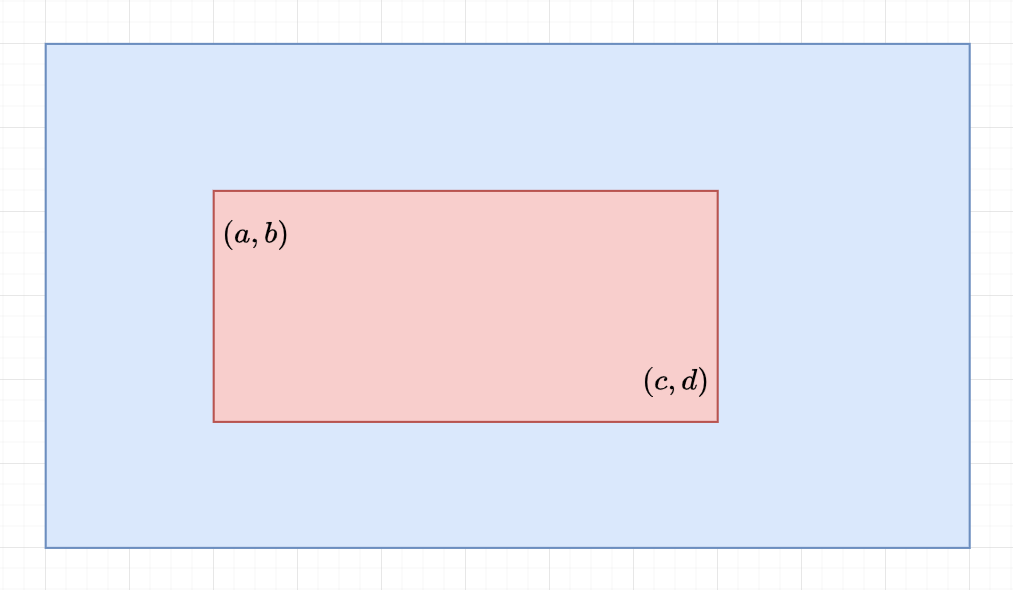
We want to find the sum in the red rectangle
\texttt{pref[x][y]}= \sum_{i=1}^x \sum_{j=1}^y a[i][j]
We will precompute the 2D Prefix Sum (the sum of rectangle from \((1,1)\) to \((x,y)\))
\texttt{sum(a,b,c,d) = pref[c][d] - pref[c][b-1] - pref[a-1][d] + pref[a-1][b-1]}
Therefore, each query is now \(O(1)\) after precomputing the 2D Prefix Sum
\texttt{pref[i][j] = pref[i-1][j] + pref[i][j-1] - pref[i-1][j-1]}
To compute the prefix sum, we do
This can be done in \(O(n^2)\)
Can you also do 2D Difference Array?
Sweep Line Algorithm
What is Sweep Line?
What is Sweep Line?
We use an imaginary line to think about problems related to segments / rectangle / triangle / circle / ... on a 2D plane
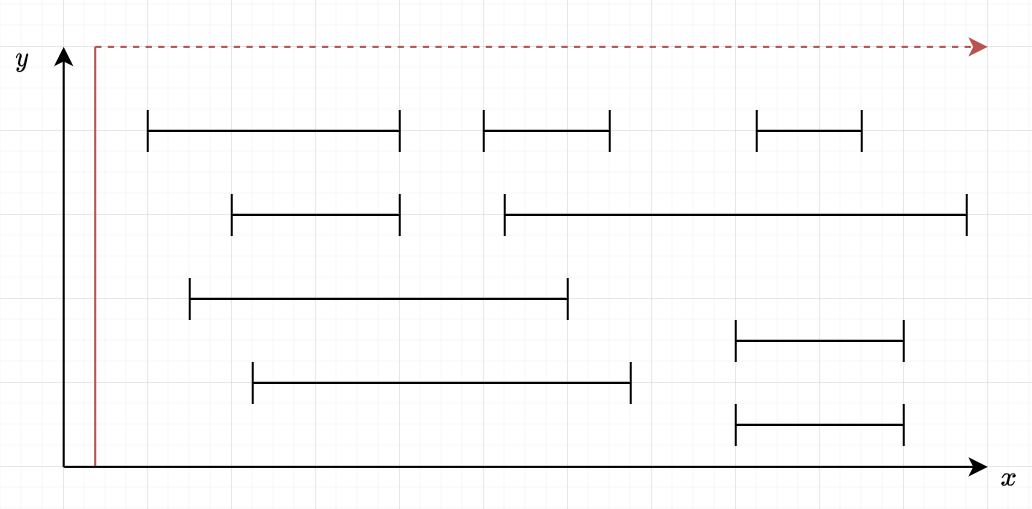
Let's look at an example!
Length of Union of Segments
You are given \(n\) segments, each covers the interval \([l_i, r_i]\). Find the total length of intervals these segments covers.
- \(1 \le n \le 10^6\)
- \(1 \le l_i, r_i \le 10^9\)
Length of Union of Segments
You are given \(n\) segments, each covers the interval \([l_i, r_i]\). Find the total length of intervals these segments covers.
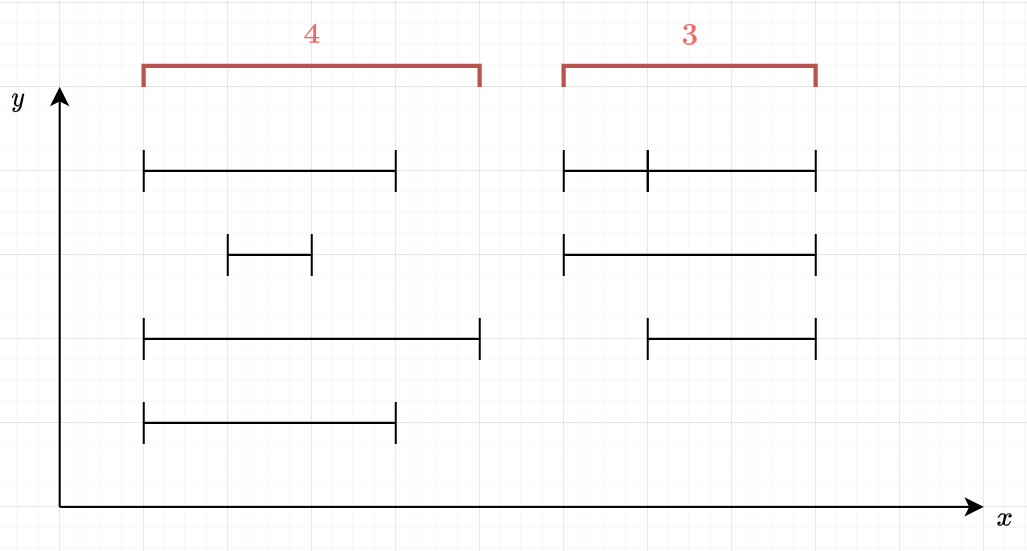
Length of Union of Segments
Think about this, let an imaginary line start from the left of all segments, and moves to the right by \(1\) unit each second
Length of Union of Segments
Think about this, let an imaginary line start from the left of all segments, and moves to the right by \(1\) unit each second
Length of Union of Segments
The only thing that actually matters are the left bound and right bound of the interval
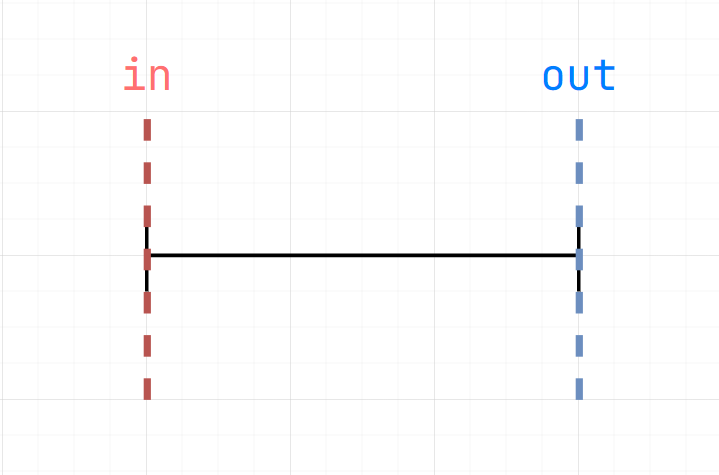
Length of Union of Segments
Solution:
- For each segment \([l,r]\), divide it into \(\{l, 1\}\) which means the line passes \(l\) and \(\{r+1, -1\}\) means the lines leaves \(r\)
- Keep track of how many segments the line passes through at this moment, and you only need to sum up how many seconds \(a > 0\)
Length of Union of Segments
map<int,int> mp;
for(int i = 0; i < n; i++){
mp[l[i]]++;
mp[r[i] + 1]--;
}
int cnt = 0, ans = 0, prev = 0;
for(auto [a,b] : mp){
if(cnt > 0) ans += cnt * (a - prev);
cnt += b;
}
cout << ans << "\n";
Code for Union of Segments
This problem is basically the same, but each day, it's either pay \(C\) or pay the sum of all services
Notice that the only price changes will happen on the endpoints of the interval of the services
Monotonic Stack
Naive Solution
For each \(i\), search \(j\) from \(i-1\) to \(1\) and check if \(a_j < a_i\)
for(int i = 1; i <= n; i++){
for(int j = i-1; j >= 1; j--){
if(arr[j] < arr[i])
ans[i] = j;
}
}O(n^2)
We will use a data structure to solve this!
Monotonic Stack maintains a strictly increasing or strictly decreasing sequence
We start from the beginning, and we want the top of the stack to be the answer we want
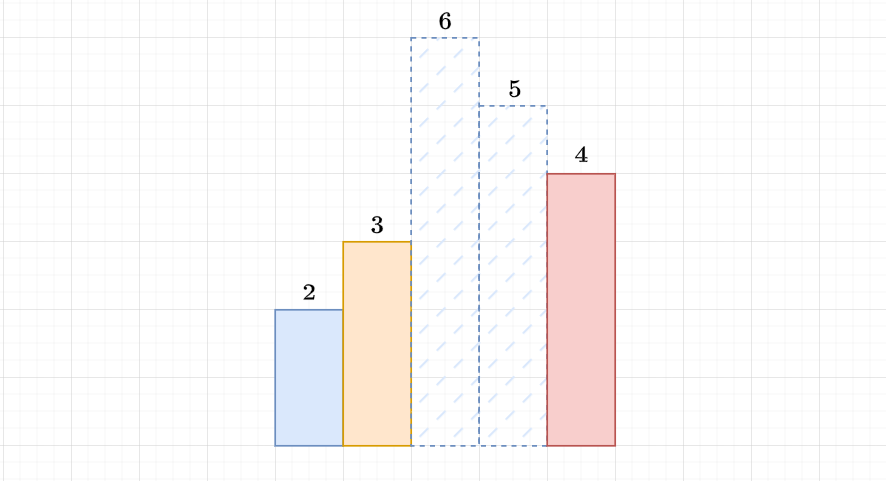
if top of stack \(> a_i\) then pop it
This gives us a way to not search for all elements, and can find answer for all \(i\) in \(O(n)\)
stack<int> st;
for(int i = 1;i <= n;i++){
while(!st.empty() && arr[st.top()] >= arr[i]){
st.pop();
}
if(!st.empty())
ans[i] = st.top();
st.push(i);
}
}
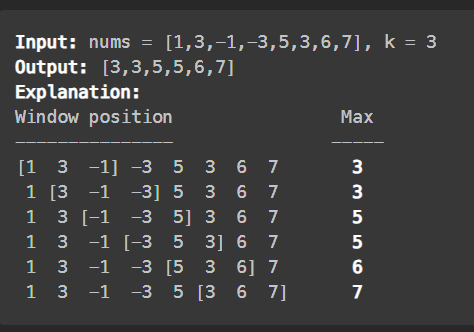
We use similar thoughts to solve this problem
I will be drawing on whiteboard since it's hard to explain without it
With this thought, we can solve this in \(O(n)\)!
deque<int> mx;
vector<int> ans;
for(int i = 0;i < n;i++){
while(!mx.empty() && i-mx.front() >= k)
mx.pop_front();
while(!mx.empty() && arr[mx.back()] <= arr[i])
mx.pop_back();
mx.push_back(i);
if(i >= k-1) ans.push_back(arr[mx.front()]);
}
There is a technique called Monotonic Stack Optimization for DP problem which we learn later that uses the same thought
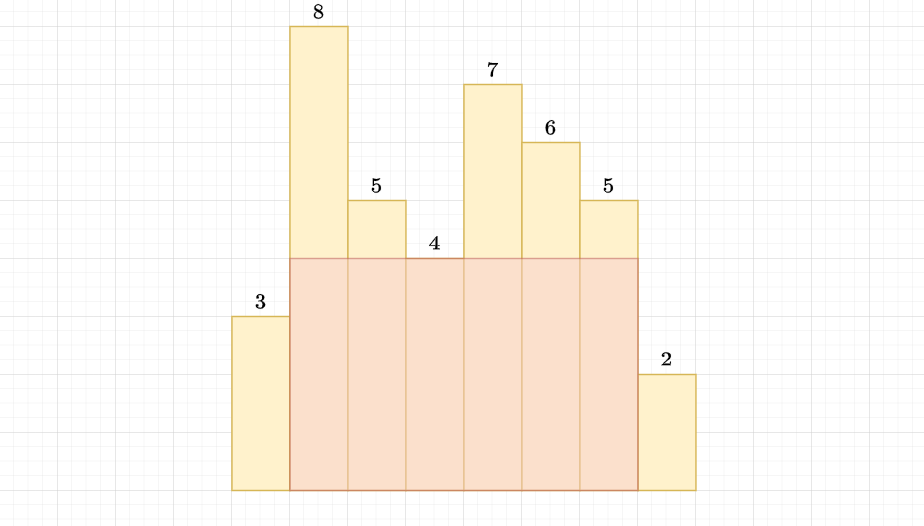
Naive Solution
Suppose we fix interval \([l,r]\), then the answer must be
$$\min_{(l,r) \in I}\{\min(h_l,\cdots,h_r)(r-l+1)\}$$
// Assume that the heights are stored in h[]
int maxArea = 0;
for(int l = 1; l <= n; l++){
int minH = h[l];
for(int r = l; r <= n; r++){
minH = min(minH ,h[r]);
maxArea = max(maxArea, minH*(r-l+1));
}
}O(n^2)
From the previous thought, we searched for the height
and fixed interval
$$\min_{(l,r) \in I}\{\min(h_l,\cdots,h_r)(r-l+1)\}$$
How about fixing height and search for interval?
How about fixing height and search for interval?
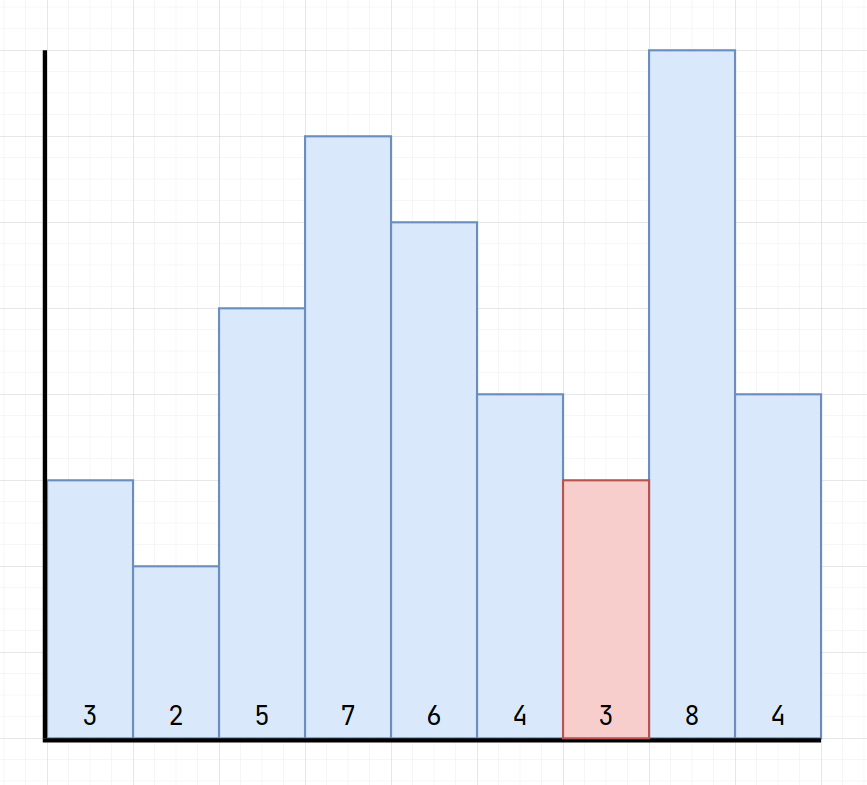
How about fixing height and search for interval?
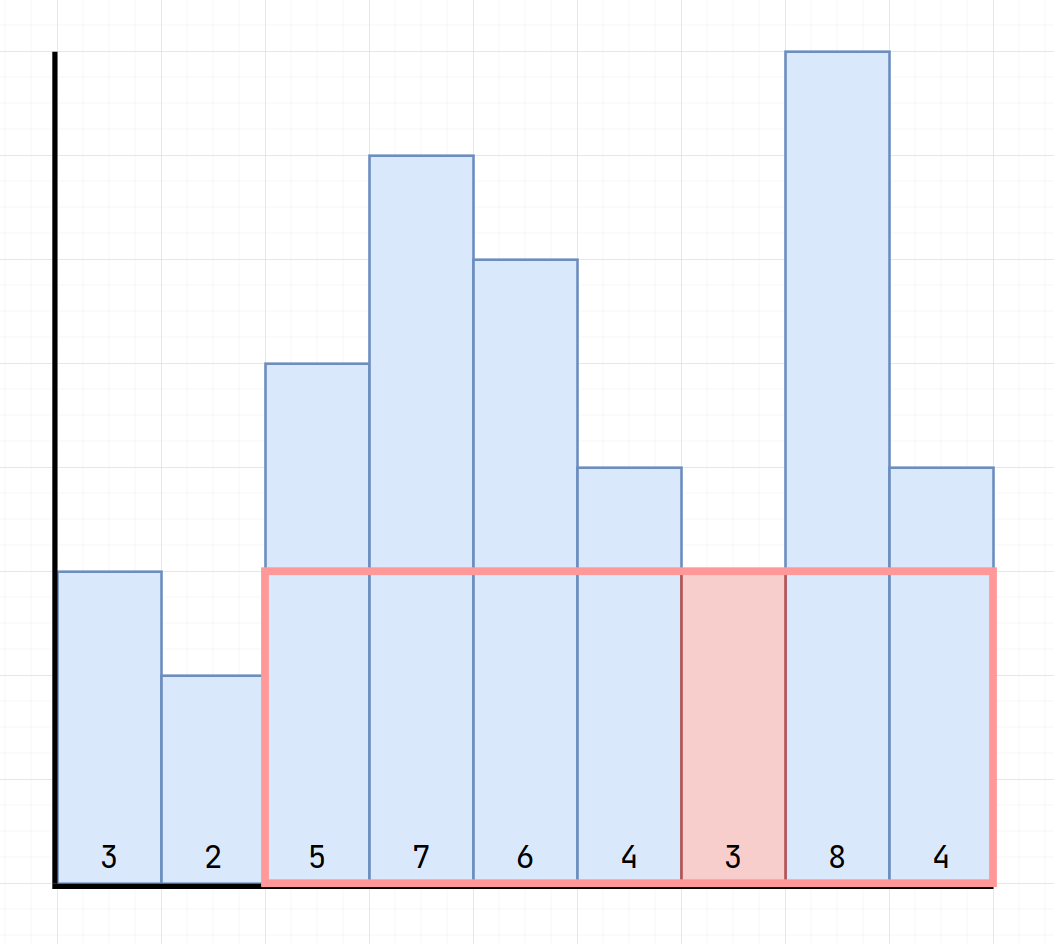
We can change the way into
$$\min_{1 \le i \le n}(h[i] \times (r[i]-l[i]+1))$$
\(l[i]\) is the next element to the "first element on left lower than \(i\)"
\(r[i]\) is the prev element to the "first element on right lower than \(i\)"
Using the way we just talked about twice
You can evaluate all \(l[i]\) and \(r[i]\) in \(O(n)\)
The solution becomes \(O(n)\)!
Today, we talked about several techniques that is common for CP
You might use these techniques a lot in CP
UMD Summer CP - Basic Techniques
By sam571128
