Introduction & Basics

UMD CP Club Summer CP

Who am I?

Cheng-Yuan (Sam) Lee

．Rising Sophomore

．ICPC Mid-Atlantic 3rd Place

．UMD CP Club President

．Codeforces Master

．AtCoder Rating \(\ge\) 2000

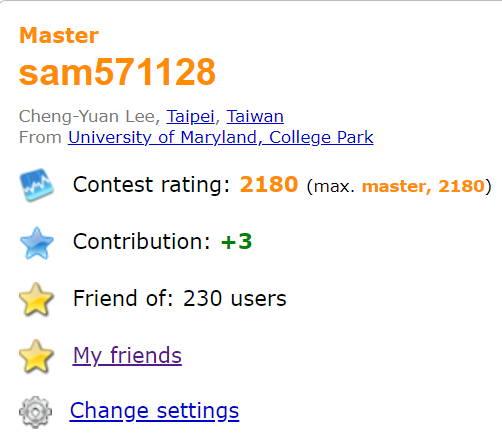
Feel free to discuss problems with me!

What is Competitive Programming

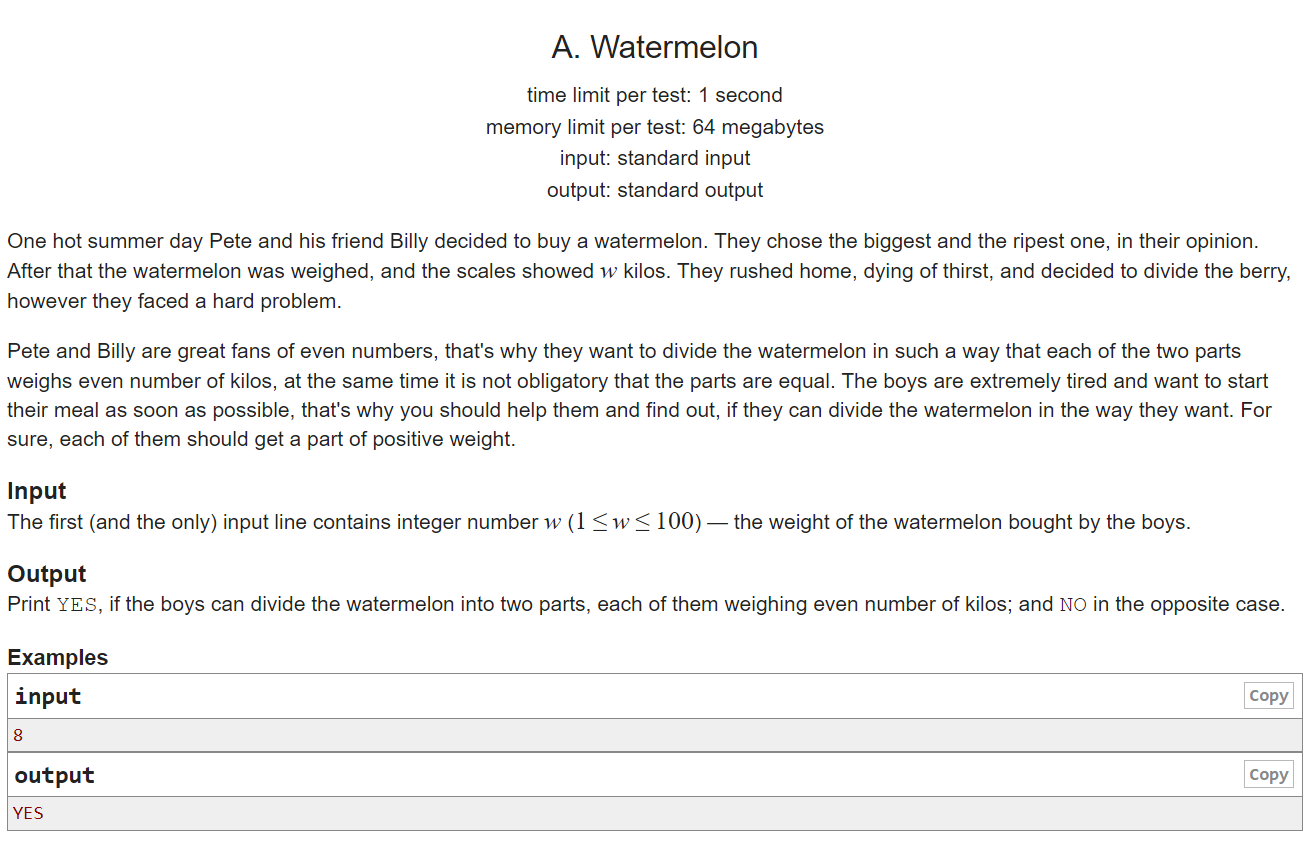
The problems are usually algorithmic

(CMSC351/451)

 

You have to come up with an algorithm

and implement It!

There are also two important parts

Time    and   Space

Time    and   Space

If Your Code didn't fit in Time

If Your Code didn't fit in Time

You get TLE

(Time Limit Exceeded)

If Your Code didn't fit in Space

You get MLE

(Memory Limit Exceeded)

If Your Code is incorrect

You get WA

(Wrong Answer)

When you finally solved a problem, you get AC !

(Accepted)

Ratings!

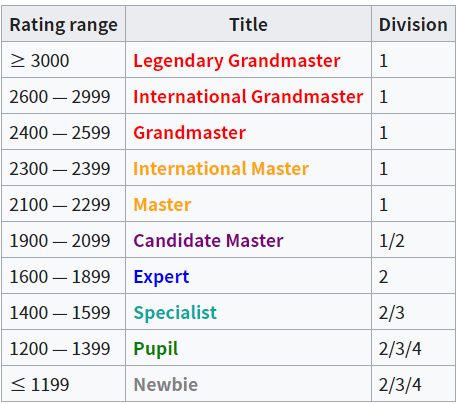
T-Shirt!

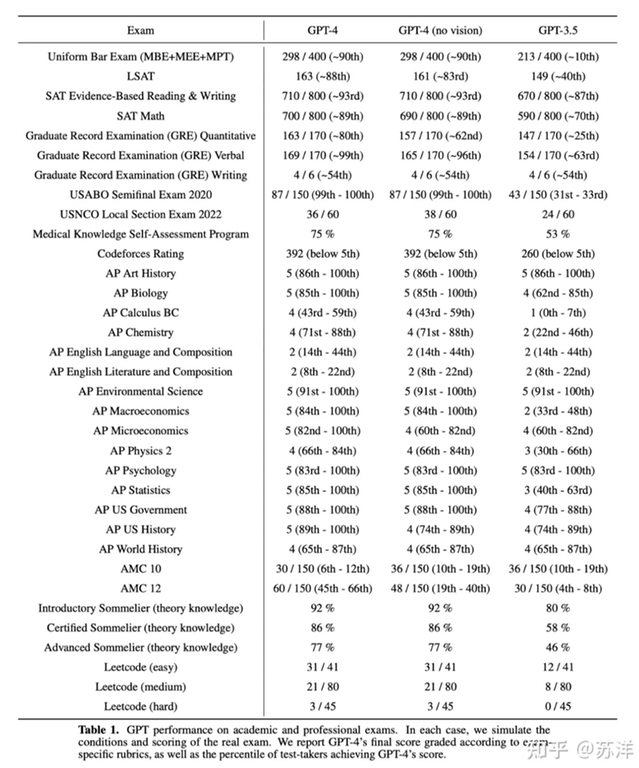
Resources

USACO Guide

CPer's Handbook

CP Algorithms

CSES Problem Set

Time Complexity

In C++

In C++

10^8 \text{ operations} \approx 1 \text { second}

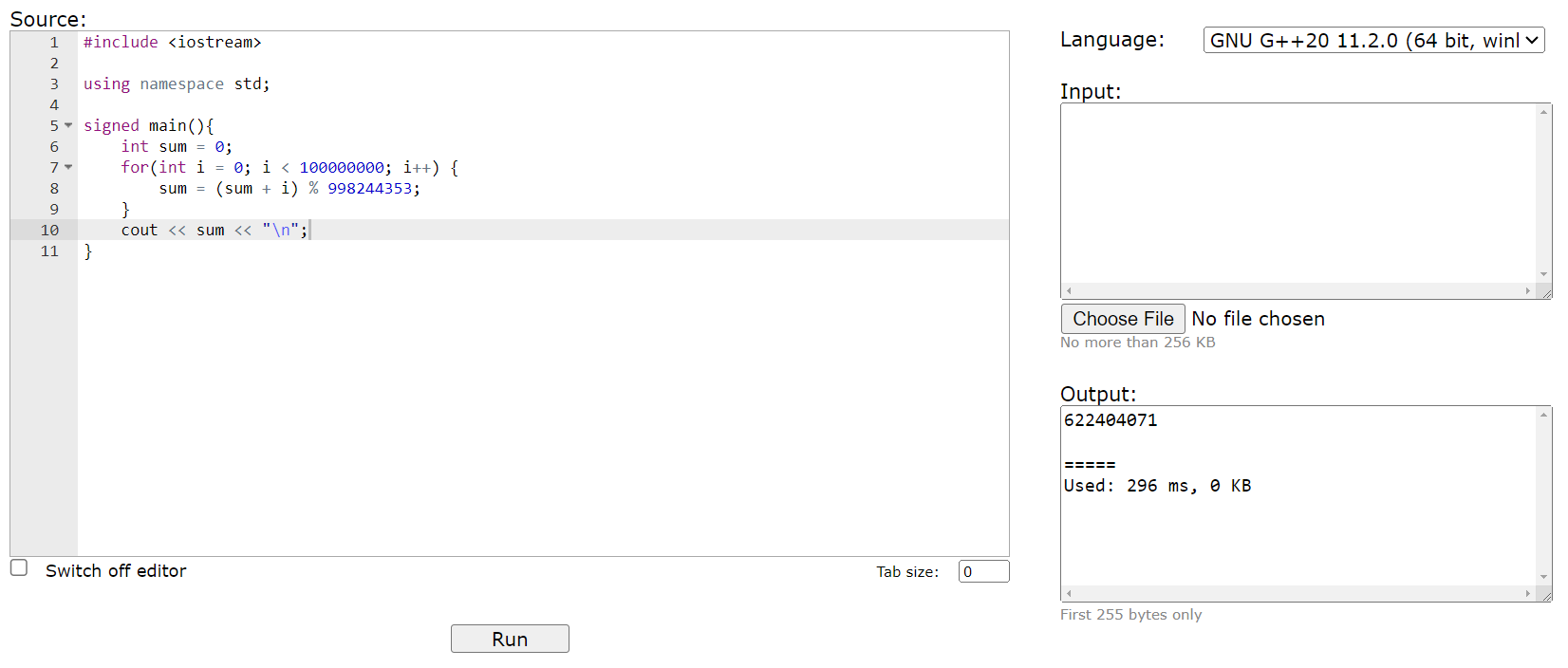
It varies from \(10^8 \sim 5 \times 10^8\)

We need a tool to approximate how many operations our code does!

Big O Notation

Big O Notation

We denote the runtime of an algorithm with

O(f(n))

where \(n\) is the input size

\(f(n)\) is the number of operations with respect to \(n\)

Big O Notation

g(n) \in O(f(n))

The formal definition of Big O is

if and only if

\exists c, n_0 \text{ s.t. } \forall n \ge n_0, g(n) \le cf(n)

Big O Notation

g(n) \in O(f(n))

The formal definition of Big O is

if and only if

\exists c, n_0 \text{ s.t. } \forall n \ge n_0, g(n) \le cf(n)

We ignore the constant factor

Big O Notation

g(n) \in O(f(n))

The other viewpoint of Big O is

if and only if

\displaystyle \lim_{n \to \infty} \frac{g(n)}{f(n)} \ne \infty

Big O Notation

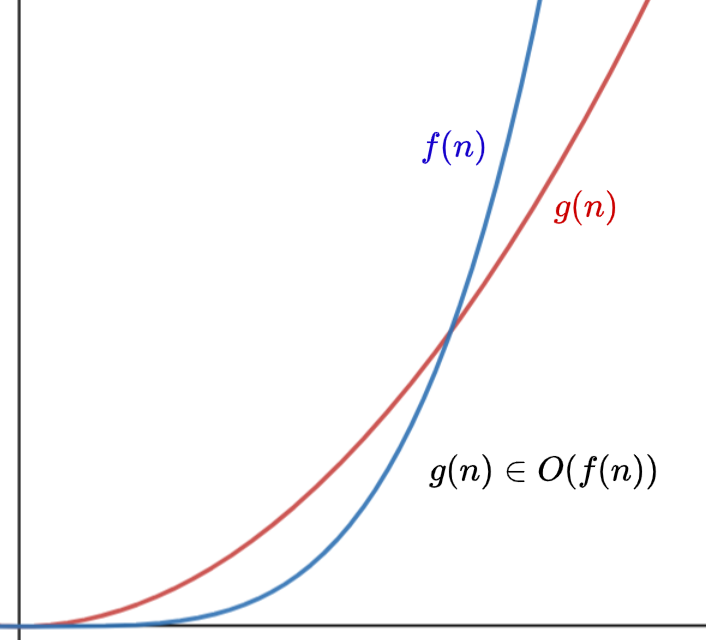
In CP, we usually plug \(n\) in

and divide by \(10^8 \sim 5 \times 10^8\)

1. Counting Loops

for (int i = 1; i <= n; i++) {
   sum += i;
}

What is the time complexity of this code?

O(n)

1. Counting Loops

for (int i = 1; i <= 2*n; i++) {
   sum += i;
}

What is the time complexity of this code?

O(n)

1. Counting Loops

for (int i = 1; i <= n; i++) {
   for (int j = 1; j <= n; j++) {
       sum += i * j;
   }
}

What is the time complexity of this code?

O(n^2)

1. Counting Loops

for (int i = 2; i <= n; i++) {
    for(int j = 2 * i; j <= n; j += i){
        isprime[j] = false;
    }
}

What is the time complexity of this code?

O(n(\frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{n}))

1. Counting Loops

for (int i = 2; i <= n; i++) {
    for(int j = 2 * i; j <= n; j += i){
        isprime[j] = false;
    }
}

What is the time complexity of this code?

O(n \log n)

1. Counting Loops

2. Recursions

int f(int x){
    if (x <= 1) {
        return 1;
    } else {
        return f(x-1) + f(x-2);
    }
}

What is the time complexity of this code?

2. Recursions

O(1.618^n)

2. Recursions

You will learn different ways to approximate time complexity of recursion in CMSC351

Recursion Tree

Substitution Method

Master's Theorem

Knowing Master's Theorem will be sufficient

Big O Notation

Programming Language

Which Language Should I Use?

In IOI (International Olympiad in Informatics)

The only allowed language is C/C++

In ICPC

The allowed languages are

C/C++, Java, Python, Kotlin

Most Competitive Programmer Uses C++

We will be using C++

Basic C++ Syntax

#include <bits/stdc++.h>

using namespace std;

int main(){
    int a, b;
    cin >> a >> b;
    cout << a+b << "\n";
}

A+B Code

#include <bits/stdc++.h>

This header includes all the common headers

cin >>
cout <<

The above input things from standard input

The bottom output things to standard output

for (int i = 0; i < n; i++) {
    //do something n times
}

while(condition) {
    //do something when condition is true
}

Loops

The range of  int  is approxiamtely

\([-2 \times 10^9, 2 \times 10^9]\)

Important!

The range of  long long  is

\([-9 \times 10^{18}, 9 \times 10^{18}]\)

There was a debate between

cin, cout and  scanf(), printf()

cin, cout

are slow!

a * b

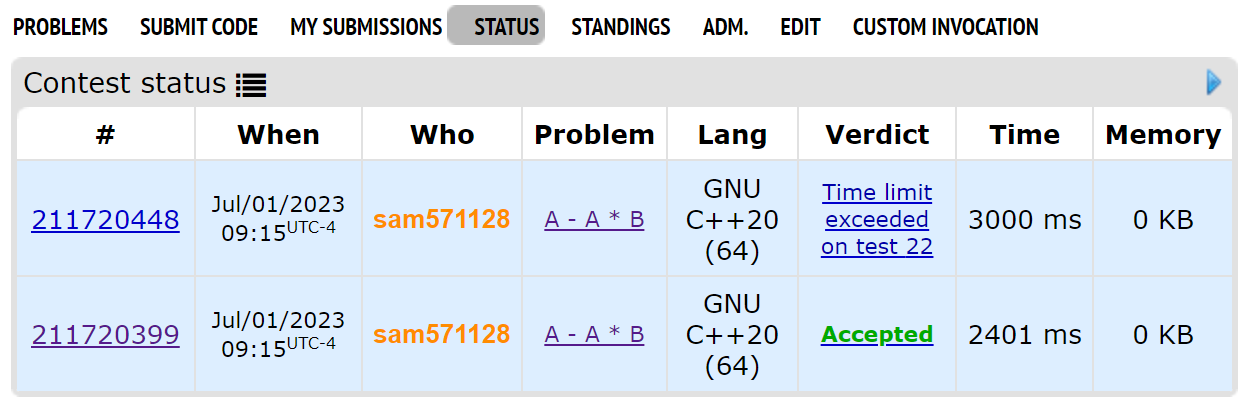
Try this problem

If you use scanf, printf

You get AC

If you use cin, cout

You get TLE

Does that mean you shouldn't use cin, cout?

NO!

ios_base::sync_with_stdio(0); cin.tie(0);

Add these two lines to your code!

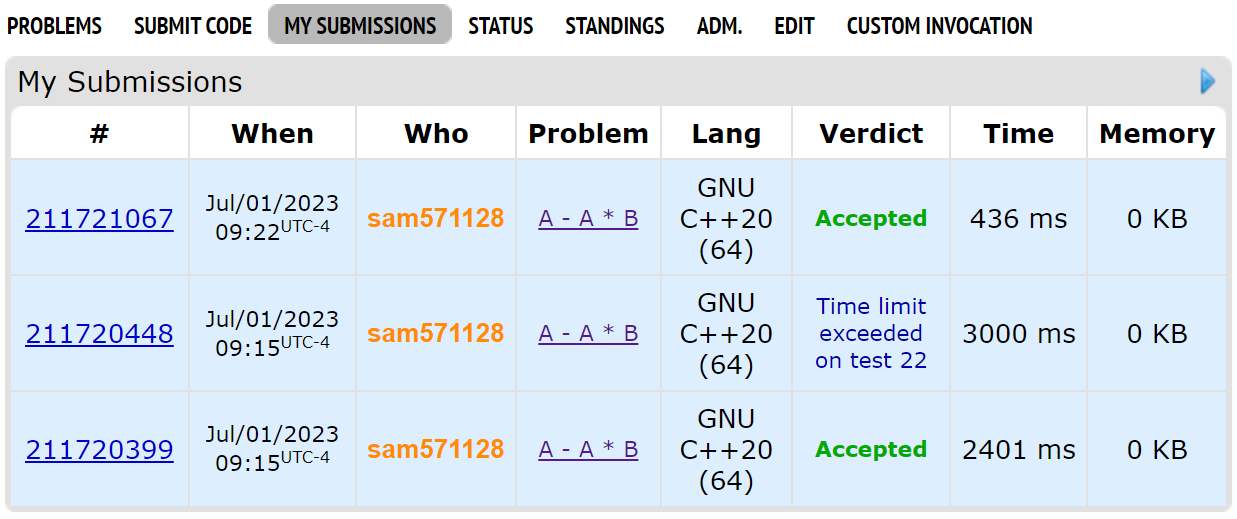
cin, cout is now 6x faster than scanf, printf !

Another Important Thing

Another Important Thing

Use "\n" instead of endl

First one uses cin, cout and endl

Second one uses cin, cout and "\n"

C++ STL & Basic Data Structures

Immutable Arrays

int arr[n];
long long arr[n];
char arr[n];
string arr[n];

An array is initialized with T arr[length]

where T is some type and length is some integer

The size cannot be changed

Immutable Arrays

int arr[n] = {1, 2, 3};
cout << arr[0] << "\n"; // 1
cout << arr[1] << "\n"; // 2
arr[1] = 0;
cout << arr[1] << "\n"; // 0

You can access elements with arr[i]

it is 0-based, the first element is arr[0]

Dynamic Arrays

There are two types of dynamic arrays

vector<T>

deque<T>

vector supports pushing back but not front

deque supports both pushing back and front

Dynamic Arrays - vector<T> 

vector<int> v;
v.push_back(1); // v = {1}
cout << v[0] << "\n"; // 1
v.push_back(2); // v = {1, 2}
v.pop_back(); // v = {1}
v.push_back(3); // v = {1, 3}
cout << v[1] << "\n"; // 3
for (int i = 0; i < v.size(); i++) {
    cout << v[i] << " ";
}

Dynamic Arrays - vector<T> 

vector<int> v(len, x); 
//initialize a vector of length len and initial element x
v[i]; //access the ith element
v.push_back(x); //add x to back
v.pop_back(); //remove last element
v.size(); //returns size of the vector
v.empty(); //returns true or false
v.resize(len); //resize the vector to len
v.clear(); //clear the vector

Dynamic Arrays - string

string in C++ is technically just vector<char>

but it also has

string s = "Hello";
s += "World";
cin >> s;
cout << s;

Dynamic Arrays - deque<T> 

deque<int> dq;
dq.push_back(1); // v = {1}
cout << dq[0] << "\n"; // 1
dq.push_back(2); // v = {1, 2}
dq.pop_front(); // v = {2}
dq.push_back(3); // v = {2, 3}
cout << dq[0] << "\n"; // 2
for (int i = 0; i < dq.size(); i++) {
    cout << dq[i] << " ";
}

Dynamic Arrays - deque<T> 

deque<int> dq(len, x); 
//initialize a deque of length len and initial element x
dq[i]; //access the ith element
dq.push_back(x); dq.push_front(x);//add x to back/front
dq.pop_back(); dq.pop_front(); //remove last/first element
dq.size(); //returns size of the deque
dq.empty(); //returns true or false
dq.resize(len); //resize the deque to len
dq.clear(); //clear the deque

You might ask, why don't we always use deque?

It has a larger constant!

How to sort an array?

In C++, there are builtin functions that are fast and easy to use!

How to sort an array?

int arr[n] = {5, 4, 3, 2, 1};
vector<int> v = {3, 4, 5, 1, 2};

sort(arr, arr+n);
sort(v.begin(), v.end());

std::sort has a time complexity of \(O(n \log n)\)

Other useful methods (requires sort)

lower_bound(v.begin(), v.end(), x);
//return the iterator to first >= x
upper_bound(v.begin(), v.end(), x);
//return the iterator to first > x
unique(v.begin(), v.end());
//if v has k unique elements, set v[0], v[1], v[k-1] to those elements

Both lower and upper bound takes \(O(\log n)\)

unique takes \(O(n)\)

Other useful methods

swap(&a, &b); //swap the value of a and b
fill(v.begin(), v.end(), x) //make all elements in range x
reverse(v.begin(), v.end()); //reverse the range
max_element(v.begin(), v.end()); //return iterator to maximum element
min_element(v.begin(), v.end()); //return iterator to minimum element
shuffle(v.begin(), v.end()); //random shuffle all elements in range

swap is \(O(1)\)

others are \(O(n)\)

ABC248D - Range Count Query

Pairs

Consider this simple task

You are given \(n\) points on 2d plane,

sort them first by \(x\) then by \(y\)

Pairs

pair<T, T> p;
p.first; //returns first element
p.second; //returns second element

pair<T,T> make_pair(T a, T b); //return a pair {a,b}
{a, b}; //same as above

Pairs

vector<pair<int,int>> v;
for (int i = 0; i < n; i++) {
    v.push_back({x[i], y[i]});
}
sort(v.begin(), v.end());

Stack

It is a Last in First Out Data Structure

stack<int> st;
st.push(x); //push back
st.pop(); //pop back
st.top(); //returns last element
st.empty(); //return true or false
st.size(); //return size of stack

UVA Rails

HackerRank - Balanced Brackets

CSES Advertisement

This is monotonic stack, we will focus on it more later

Queue

It is a First in First Out Data Structure

queue<int> q;
q.push(x); //push front
q.pop(); //pop front
q.front(); //returns first element
q.empty(); //return true or false
q.size(); //return size of queue

ABC216D - Pair of Balls

Queue

This data structure is used for BFS

We will use it more when we talk about it

Priority Queue (Heap)

You can simply used it as a sorted queue

priority_queue<int> pq;
pq.push(x); //push x into the queue
pq.pop(); //pop the largest element
pq.top(); //returns the largest element
pq.empty(); //return true or false
pq.size(); //return size of queue

push and pop are \(O(\log n)\)

Priority Queue (Heap)

You can also create min heap (default is max heap)

priority_queue<int, vector<int>, greater<>> pq;
pq.push(x); //push x into the queue
pq.pop(); //pop the smallest element
pq.top(); //returns the smallest element
pq.empty(); //return true or false
pq.size(); //return size of queue

CSES - Stick Division

This data structure is used the most in Greedy algorithms

Codeforces 1526C2 - Potions

Binary Search Tree

There are two builtin binary search trees

set<T>

map<K,V>

Both are ordered

set

set<int> st;
st.insert(x); //add x to set
st.erase(x); //remove x from set
st.count(x); //most used as finding x
st.find(x); //it is harder to use than count
st.empty(); //return true or false
st.size(); //return size
st.lower_bound(x); //return iterator to first >= x
st.upper_bound(x); //return iterator to first > x

multiset

multiset<int> st;
st.insert(x); //add x to set, O(log n)
st.erase(x); //remove all x from set, O(log n)
st.count(x); //count the number of x, O(log n)
st.find(x); //find the first x, O(log n)
st.empty(); //return true or false,  O(1)
st.size(); //return size,  O(1)
st.lower_bound(x); //return iterator to first >= x, O(log n)
st.upper_bound(x); //return iterator to first > x, O(log n)

multiset

If you only want to remove an element

Use st.erase(st.find(x));

map

You can use it as an array for any data type

map<string, int> mp;
mp["hello"] = 1; //O(log n)
mp.insert("a", 2); // O(log n)
cout << mp["a"] << "\n"; // 2
mp.erase("hello"); // O(log n)

//other things are the same as set
mp.erase(Key); //remove Key from map O(log n)
mp.count(Key); //check if Key exists in map O(log n)
mp.find(Key); // O(log n)
mp.lower_bound(key); // O(log n)
mp.upper_bound(key); // O(log n)

unordered_map (hash table)

Same as map, but doesn't support set operations

Everything becomes \(O(1)\) (expected)

CSES - Traffic Lights

Codeforces 1500A - Going Home

These are just the basics, but it is important to know them

We will start discussing actual algorithms in the following weeks

UMD Summer CP - Introduction & Basics

By sam571128

Made with Slides.com

UMD Summer CP - Introduction & Basics

  • 302

More from sam571128