離線演算法
(Offline Algorithms)
目錄
在線 v.s. 離線
莫隊算法
整體二分搜
CDQ 分治
在線 v.s. 離線
在線 (Online)
依序處理輸入或詢問
離線 (Offline)
將輸入或詢問經過排序等方式處理
對於一些題目,有時候會發現不好處理
例如: 區間 Mex、區間有幾個數字等等
仔細想想看過後,會發現其實把詢問排序後會較簡單!
給你一個 \(n\) 項的陣列
每次詢問 \([l,r]\) 之間有幾個相異數字
\(1 \le n \le 10^5\)
我們能夠發現,其實離線能夠將問題簡化許多!
持久化線段樹
排序之後,正常的線段樹
在題目沒有強制在線時
先考慮一下離線作法會比較好!
強烈建議
莫隊算法
(Mo's Algorithm)
同樣的,我們來看看同一題
給你一個 \(n\) 項的陣列
每次詢問 \([l,r]\) 之間有幾個相異數字
\(1 \le n \le 10^5\)
要是我們不會線段樹或 BIT 呢?
如果,我們今天知道 \([l,r]\) 的答案
我們可以在 \(O(1)\) 或 \(O(\log n)\) 的時間
找到對於以下區間的答案
\([l,r-1],[l,r+1],[l-1,r],[l+1,r]\)
如果,我們今天知道 \([l,r]\) 的答案
我們可以在 \(O(1)\) 或 \(O(\log n)\) 的時間
找到對於以下區間的答案
\([l,r-1],[l,r+1],[l-1,r],[l+1,r]\)
1
3
2
3
2
4
5
Answer: 2
\(l = 1, r = 2\)
Action: None
如果,我們今天知道 \([l,r]\) 的答案
我們可以在 \(O(1)\) 或 \(O(\log n)\) 的時間
找到對於以下區間的答案
\([l,r-1],[l,r+1],[l-1,r],[l+1,r]\)
1
3
2
3
2
4
5
Answer: 3
\(l = 1, r = 3\)
Action: \(r = r + 1\)
如果,我們今天知道 \([l,r]\) 的答案
我們可以在 \(O(1)\) 或 \(O(\log n)\) 的時間
找到對於以下區間的答案
\([l,r-1],[l,r+1],[l-1,r],[l+1,r]\)
1
3
2
3
2
4
5
Answer: 3
\(l = 1, r = 4\)
Action: \(r = r + 1\)
如果,我們今天知道 \([l,r]\) 的答案
我們可以在 \(O(1)\) 或 \(O(\log n)\) 的時間
找到對於以下區間的答案
\([l,r-1],[l,r+1],[l-1,r],[l+1,r]\)
1
3
2
3
2
4
5
Answer: 2
\(l = 2, r = 4\)
Action: \(l = l + 1\)
如果,我們今天知道 \([l,r]\) 的答案
我們可以在 \(O(1)\) 或 \(O(\log n)\) 的時間
找到對於以下區間的答案
\([l,r-1],[l,r+1],[l-1,r],[l+1,r]\)
1
3
2
3
2
4
5
Answer: 2
\(l = 2, r = 3\)
Action: \(r = r - 1\)
如果,我們今天知道 \([l,r]\) 的答案
我們可以在 \(O(1)\) 或 \(O(\log n)\) 的時間
找到對於以下區間的答案
\([l,r-1],[l,r+1],[l-1,r],[l+1,r]\)
1
3
2
3
2
4
5
Answer: 3
\(l = 1, r = 3\)
Action: \(l = l - 1\)
我們可以寫出這樣的 Code
vector<query> queries;
int l = 1, r = 0, ans = 0;
for(auto [ql, qr] : queries){
while(l <= ql) del(arr[l]), l++; //計算 [l+1,r]
while(r <= qr) r++, add(arr[r]); //計算 [l,r+1]
while(l > ql) l--, add(arr[l]); //計算 [l-1,r]
while(r > qr) del(arr[r]), r--; //計算 [l-1,r]
res[id] = ans;
}我們可以寫出這樣的 Code
vector<query> queries;
int l = 1, r = 0, ans = 0;
for(auto [ql, qr, id] : queries){
while(l < ql) del(arr[l++]); //計算 [l+1,r]
while(r < qr) add(arr[++r]); //計算 [l,r+1]
while(l > ql) add(arr[--l]); //計算 [l-1,r]
while(r > qr) del(arr[r--]); //計算 [l-1,r]
res[id] = ans;
}不過,這樣的時間複雜度是多少?
假設 add 和 del 的操作複雜度為 \(O(x)\)
每一次指針的移動最多為 \(O(n)\) 次
時間複雜度為 \(O(qnx)\)
若 \(O(x) \in O(1)\),則複雜度跟暴力其實一樣
能不能更好?
考慮對陣列進行分塊
以每 \(B\) 個數字為一塊


我們把詢問 \([l,r]\)
以 \(l\) 在的塊進行排序
再以 \(r\) 進行排序
struct query{
int l,r,id;
bool operator < (query b){
if(l/k == b.l/k) return r < b.r;
return l/k < b.l/k;
}
};複雜度分析 (設 \(\lceil \frac n B \rceil\) 為塊數)
左界在同一塊時,一次最多移動 \(B\)
從某一塊走到另一塊時,一次最多移動 \(2B\)
左界最多移動 \(O(qB +2B\lceil \frac{n}{B} \rceil) = O(qB+n)\)
右界在左界在同一塊時,最多移動 \(n\) 格
最多移動 \(n \lceil \frac{n}{B} \rceil\) 格
總時間複雜度為 \(O(qB+n \lceil \frac{n}{B} \rceil)\)
複雜度分析 (設 \(\lceil \frac n B \rceil\) 為塊數)
右界在左界在同一塊時,最多移動 \(n\) 格
最多移動 \(n \lceil \frac{n}{B} \rceil\) 格
總時間複雜度為 \(O(qB+n \lceil \frac{n}{B} \rceil)\)
若要使複雜度最小,根據算幾不等式
\(qB = n \lceil \frac{n}{B} \rceil\)
會有最小答案
得 \(B = \frac{n}{\sqrt{q}}\),複雜度為 \(O(n \sqrt{q})\)
整份莫隊的模板
int k;
struct query{
int l,r;
bool operator < (query b){
if(l/k == b.l/k) return r/k < b.r/k;
return l/k < b.l/k;
}
};
void add(int x){
//增加數字到區間
}
void del(int x){
//減少區間的數字
}
signed main(){
int n, q;
cin >> n >> q;
k = sqrt(n);
//輸入陣列
vector<query> queries;
for(int i = 0;i < q;i++){
int l,r;
cin >> l >> r;
queries.push_back({l,r,i});
}
sort(queries.begin(),queries.end());
int l = 1, r = 0, ans = 0;
for(auto [ql, qr, id] : queries){
while(l < ql) del(arr[l++]); //計算 [l+1,r]
while(r < qr) add(arr[++r]); //計算 [l,r+1]
while(l > ql) add(arr[--l]); //計算 [l-1,r]
while(r > qr) del(arr[r--]); //計算 [l-1,r]
res[id] = ans;
}
}就這麼簡單!
(基本上改 add, del 即可)
練習題
帶修改莫隊
給你一個 \(n\) 項的陣列,與 \(q\) 次操作
1. 詢問 \([l,r]\) 之間有幾個相異數字
2. 將 \(a_i\) 改為 \(x\)
這個題目,多增加了一個單點修改的條件
整個問題就變得困難許多了!
如果使用在線作法
可能要使用樹套樹
(BIT 存持久化線段樹)
實在是太麻煩了!
我們再次考慮用莫隊!
將詢問 \([l,r]\)
改成是在時間 \(t\) 時的 \([l,r,t]\)
(\(t\) 是第幾次修改)
每次可以在 \(O(1)\) 的時間找到
\([l-1,r,t],[l+1,r,t],[l,r-1,t]\)
\([l,r+1,t],[l,r,t-1],[l,r,t+1]\)
至於對這些詢問的排序方式呢?
照 \(l\) 在的塊先排序
接著照 \(r\) 在的塊排序
最後再比較 \(t\) 的大小
假設塊的大小為 \(B\)
我們來分析一下時間複雜度
我們在此對 \(l,r,t\) 的移動次數分別分析
- \(l\): 同塊最多移動 \(O(B)\) 次,換一塊最多 \(O(2B)\),複雜度為 \(O(qB)\)
- \(r\): \(r\) 同塊最多移動 \(O(B)\),換一塊最多 \(O(2B)\),在 \(l\) 換塊時,最多移動 \(n\) 次,複雜度為 \(O(qB+n\frac{n}{B})\)
- \(t\): 對於每次 \(r\) 同塊時,最多移動 \(q\) 次,最多移動 \(O(q \frac{n^2}{B^2})\)
總複雜度為 \(O(qB+q\frac{n^2}{B^2} + \frac{n}{B})\)
\(O(qB+q\frac{n^2}{B^2} + \frac{n}{B})\)
如果要找到準確的 \(B\) 的大小會很醜
我們通常會直接取 \(B = n^{\frac{2}{3}}\)
得總複雜度為 \(O(qn^{\frac 2 3} + qn^{\frac 2 3}+n^{\frac 1 3})\)
若設 \(n=q\),總複雜度為 \(O(n^{\frac 5 3})\)
對詢問的排序
struct query{
int l, r, t, id;
bool operator < (query b){
if(l/k==b.l/k){
//l的塊相同
if(r/k==b.r/k){
//r的塊相同
return t < b.t;
}
return r/k < b.r/k;
}
return l/k < b.l/k;
}
};整份模板
int k;
struct query{
int l, r, t, id;
bool operator < (query b){
return (l/k==b.l/k ? (r/k == b.r/k ? t < b.t : r/k < b.r/k) : l/k < b.l/k);
}
} Q[N];
struct upd{
int pos,x;
} M[N];
void add(int val){
//增加數字
}
void del(int val){
//減少數字
}
void modify(query x, upd &y){
//修改數字
if(x.l <= y.pos && y.pos <= x.r){
del(arr[y.pos]);
add(y.x);
}
swap(arr[y.pos],y.x);
}
signed main(){
fastio
int n, m;
cin >> n >> m;
k = pow(n,(double)2/(double)3);
for(int i = 1;i <= n;i++) cin >> arr[i];
int tid = 0, qid = 0;
for(int i = 0;i < m;i++){
char q;
cin >> q;
if(q=='Q'){
int l, r;
cin >> l >> r;
Q[qid] = {l,r,tid,qid};
qid++;
}else{
int x, val;
cin >> x >> val;
++tid;
M[tid] = {x,val};
}
}
sort(Q,Q+qid);
int l = 1, r = 0, t = 0;
for(int i = 0;i < qid;i++){
auto q = Q[i];
while(l < q.l) del(arr[l++]);
while(l > q.l) add(arr[--l]);
while(r < q.r) add(arr[++r]);
while(r > q.r) del(arr[r--]);
while(t < q.t) modify(Q[i],M[++t]);
while(t > q.t) modify(Q[i],M[t--]);
ans[q.id] = tmp;
}
for(int i = 0;i < qid;i++) cout << ans[i] << "\n";
}練習題
回滾莫隊
(Rollback Mo's Algorithm)
給你一個 \(n\) 項的陣列,有 \(q\) 次詢問
每次詢問區間 \([l,r]\) 當中 \(\max(cnt_x \times x)\) 的值
既然我們一直在講莫隊,那我們就來用莫隊ㄅ
不過你會發現
在進行 加入數字 的操作時
我們可以很輕易的 \(O(1)\) 解決
但刪除數字呢?
void add(int val){
cnt[val]++;
tmp = max(cnt[val]*val,tmp);
}
void del(int val){
//How???
}Add 和 Del
刪除很難怎麼辦??
那如果我們會 回復上一次操作 呢?
stack<pair<int,int>> stk;
void add(int val){
stk.push({val,res});
cnt[val]++;
res = max(cnt[val]*val,res);
}
void rollback(){
assert(!stk.empty());
auto [val, tmp] = stk.top(); stk.pop();
cnt[val]--;
res = tmp;
}
Add 和 Rollback!
如果要處理 \([l,r]\) 的詢問怎麼做?
\(l,r\) 同塊? 直接暴力做完,複雜度 \(O(B)\)
不同塊?
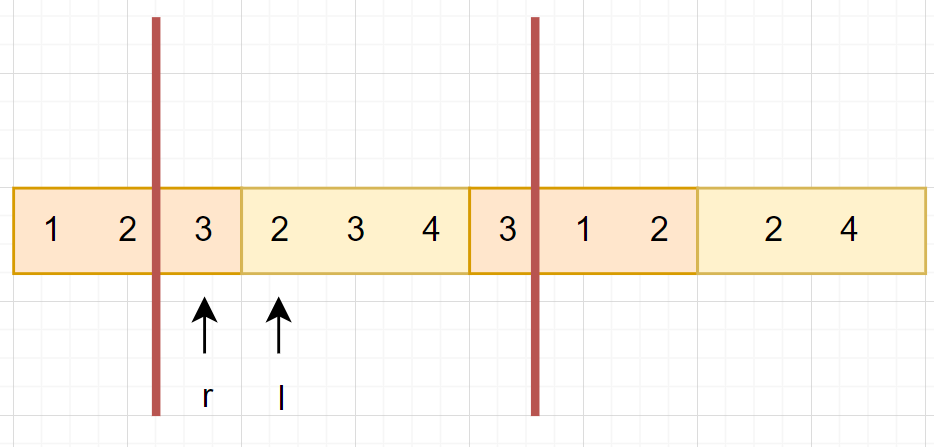
我們將 \(r\) 放置在詢問左界的塊的最後
把 \(l\) 放置在詢問左界的塊 + 1 的前面
會發現這樣在移動的時候,只會有加值的操作

1. 先把 \(r\) 往右延伸區間
2. 把 \(l\) 往前延伸區間
3. 回朔 \(l\)
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
先移動 \(r\)
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
先移動 \(r\)
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
先移動 \(r\)
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
再移動 \(l\)
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
做完紅色的詢問了
Rollback!
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
做完紅色的詢問了
Rollback!
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
做完紅色的詢問了
Rollback!
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
下一個詢問
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
下一個詢問
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
下一個詢問
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
做完了,回滾!
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
做完了,回滾!
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
不同塊了,怎麼辦?
rollback \(r\)!
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
不同塊了,怎麼辦?
rollback \(r\)!
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
不同塊了,怎麼辦?
rollback \(r\)!
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
不同塊了,怎麼辦?
rollback \(r\)!
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
不同塊了,怎麼辦?
rollback \(r\)!
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
把 \(l,r\) 直接移到他們該去的地方
\(1\)
\(2\)
\(3\)
\(2\)
\(4\)
\(1\)
\(2\)
\(2\)
\(l\)
\(r\)
(紅色是當前的詢問,黃色是下一次詢問)
把 \(l,r\) 直接移到他們該去的地方
回滾莫隊就是這樣!
我們來分析時間複雜度
複雜度分析:
\(l\): 每次詢問完和 rollback 時最多移動 \(O(2B)\)
換塊最多移動 \(O(B)\)
\(r\): 在 \(l\) 同塊時,最多移動 \(O(n)\)
總共最多移動 \(O(nB)\)
\(l,r\) 同塊時,最多移動 \(O(B)\)
時間複雜度: \(O(qB+n\frac{n}{B})\)
(取 \(B = \frac{n}{\sqrt{q}}\) 時,有 \(O(n \sqrt{q})\))
回滾莫隊模板
struct query{
int l,r,id;
bool operator < (query b){
return (l/k==b.l/k ? r < b.r : l/k < b.l/k);
}
};
void add(int val){
//加入數字
}
void rollback(){
//Rollback
}
signed main(){
fastio
int n,q;
cin >> n >> q;
k = sqrt(n);
for(int i = 1;i <= n;i++){
cin >> arr[i];
}
vector<query> queries;
int ans[q];
for(int i = 0;i < q;i++){
int l,r;
cin >> l >> r;
if(l/k == r/k){
for(int j = l;j <= r;j++){
add(arr[j]);
}
ans[i] = res;
for(int j = l;j <= r;j++){
rollback();
}
}
queries.push_back({l,r,i});
}
sort(queries.begin(),queries.end());
int lst = -1, l = 1, r = 0;
for(auto [ql,qr,id] : queries){
if(ql/k == qr/k) continue;
if(ql/k!=lst){
while(!stk.empty()) rollback();
l = (ql/k+1)*k, r = (ql/k+1)*k-1;
lst = ql/k;
}
while(r < qr) add(arr[++r]);
while(l > ql) add(arr[--l]);
ans[id] = res;
while(l < (ql/k+1)*k) rollback(), l++;
}
for(int i = 0;i < q;i++) cout << ans[i] << "\n";
}練習題
CF EDU DSU - Number of Connect Components on Segments
區間 Mex (我不知道哪裡有)
Codeforces 840D - Destiny (有分治或隨機做法)
整體二分搜
(Parallel Binary Search)
在陣列中找第 \(k\) 小
給你一個 \(n\) 項的陣列 (\(a_i \le C\))
請找到第 \(k\) 小的數字是誰
(不使用排序的話)
在陣列中找第 \(k\) 小
給你一個 \(n\) 項的陣列 (\(a_i \le C\))
請找到第 \(k\) 小的數字是誰
(不使用排序的話)
二分搜!
每次去找 \(x\) ,數有幾個數字比他小
\(O(n \log C)\)
多次在陣列中找第 \(k\) 小
給你一個 \(n\) 項的陣列 (\(a_i \le C\))
接著有 \(q\) 次詢問
每次第 \(k\) 小的數字是誰
(不使用排序的話)
\(q\) 次二分搜!
時間複雜度: \(O(q n \log C)\)
多次在陣列中找第 \(k\) 小
給你一個 \(n\) 項的陣列 (\(a_i \le C\))
接著有 \(q\) 次詢問
每次第 \(k\) 小的數字是誰
(不使用排序的話)
\(q\) 次二分搜!
時間複雜度: \(O(q n \log C)\)
太慢了吧!
多次在陣列中找第 \(k\) 小
如果我們把所有二分搜一起做呢?
欸? 好像會變得比較好欸
這種方式就叫做 整體二分搜
多次在陣列中找第 \(k\) 小
而整體二分搜通常有兩種實作方式
1. 遞迴型 (很像分治)
2. 迭代型
我們一起來看看他們分別怎麼寫
多次在陣列中找第 \(k\) 小
遞迴型的整體二分搜
struct query{
int id, k; //第幾個詢問,找第 k 大
}
int ans[N], pref[N];
void solve(int l, int r, vector<query> q){
vector<query> q1, q2; //分別存要往左和往右二分搜的詢問
int mid = (l+r)/2;
if(l == r){
//二分搜到底了
for(auto [id, k] : q){
ans[id] = l;
}
return;
}
//找陣列中有幾個數字 <= mid
int cnt = pref[mid];
for(auto [id, k] : q){
if(cnt >= k){
//如果 <= mid 的數字 >= k,往左二分搜
q1.push_back({id,k});
}else{
//如果 <= mid 的數字 < k,往右二分搜
q2.push_back({id,k});
}
}
solve(l, mid, q1), solve(mid+1, r, q2);
}多次在陣列中找第 \(k\) 小
迭代型的整體二分搜
struct query{
int l, r, k; //二分搜區間,找第 k 大
};
int ans[N], cnt[N];
vector<query> queries;
void parallel_binary_search(){
while(true){
//while 最多只會執行 log C 次
bool done = true;
vector<vector<int>> ask(N);
for(int i = 0;i < queries.size();i++){
if(queries[i].l < queries[i].r){
int mid = (queries[i].l + queries[i].r)/2;
ask[mid].push_back(i);
done = false;
}
}
if(done) break; //搜尋完了
int now = 0;
for(int i = 0;i < N;i++){
now += cnt[i];
for(auto id : ask[i]){
if(now >= queries[id].k){
//如果 <= mid 的數量 >= k,往左找
queries[id].r = mid;
}else{
//如果 <= mid 的數量 < k,往右找
queries[id].l = mid+1;
}
}
}
}
for(int i = 0;i < queries.size();i++){
cout << queries[i].l << "\n";
}
}不過剛剛的問題實在太簡單了
我們把題目改成
「多次詢問區間第 \(k\) 大的數字」
看過這題的人應該都知道
原本可能要使用持久化線段樹等資結
不過! 整體二分可以離線輕鬆解決!
區間第 \(k\) 大
因為要維護區間 \(\le\) 某數的數量
我們會搭配 BIT
而想法與剛剛十分類似
因此我們一起來看看這要怎麼做
區間第 \(k\) 大
struct num{
int pos, x; //原陣列上的位置,大小
};
struct query{
int l, r, id, k; //詢問區間、第幾個、找第 k 大
};
void update(int pos, int val); //BIT 的更新
void query(int pos); //BIT 的詢問
int ans[N];
void solve(int l, int r, vector<num> arr, vector<query> q){
//l,r 是二分搜的區間、arr 是原陣列在 [l,r] 值域的數字
int mid = (l+r)/2;
vector<num> arr1, arr2;
vector<query> q1, q2;
if(l == r){
//二分搜完了
for(auto [ql, qr, id, k] : q){
ans[id] = l;
}
return;
}
for(auto [pos, x] : arr){
if(x <= mid){
//如果數字 <= mid,我們在 BIT 上的 pos 加值
arr1.push_back({pos,x}), update(pos,1);
}else{
arr2.push_back({pos,x});
}
}
for(auto [ql, qr, id, k] : q){
int cnt = query(qr)-query(ql-1);
if(k <= cnt){
//如果 k <= cnt,往左搜尋
q1.push_back({ql,qr,id,k});
}else{
//如果 k > cnt,往右搜尋
q2.push_back({ql,qr,id,k-cnt});
}
}
//清空 BIT
for(auto [pos, x] : arr){
if(x <= mid){
update(pos,-1);
}
}
solve(l, mid, arr1, q1), solve(mid+1, r, arr2, q2);
}參考寫法 (遞迴型)
區間第 \(k\) 大
不過這樣複雜度是 \(O(q \log^2 n)\)
其實比持久化線段樹多了一個 \(O(\log n)\)
但是寫起來會比持久化來得簡單
而且,可以處理帶修改區間第 k 大
(但我們這裡不提?)
POI 2011 - Meteors
有 \(n\) 個星球和 \(m\) 個太空站
每個太空站皆由一個星球所佔領
接下來有 \(k\) 場隕石雨
每一場隕石雨會對區間 \([l,r]\) 下 \(o_i\) 個隕石
每個星球想要收集 \(p_i\) 個隕石
請輸出每個星球最少要經過幾場隕石雨才能收集到他們所想要的隕石數量
這題其實也是整體二分搜很經典的題目
對每個星球二分搜他們各自的答案
不過一起做就好了
練習題
CDQ 分治
(又稱操作分治)
CDQ 的概念
對於區間 \([l,r]\),我們會對它進行以下計算 \((m = \frac{l+r}{2})\)
1. 將其分成 \([l,m]\), \([m+1,r]\)
2. 計算出 \([l,m]\), \([m+1,r]\) 的答案
3. 計算 \([l,m]\) 對 \([m+1,r]\) 造成的影響
與正常分治不同的是,\([l,m]\) 的答案可能會影響 \([m+1,r]\)
二維偏序問題 (逆序數對)
給你兩個陣列 \(A,B\),問總共有幾對 \(i,j\) 滿足
\((a_i < a_j )\land (b_i < b_j)\)
這個問題我們可以很輕易地用 BIT 解決
但我們來用分治寫一次!
二維偏序問題 (逆序數對)
1. 先把數對照 \(a_i\) 排序
2. 用分治的方式去計算 \(b_i < b_j\) 的答案
分治的過程
假設我們要計算 \([l,r]\) 的答案數量
我們先算出 \([l,m]\) 和 \([m+1,r]\) 的答案
並將 \([l,m]\) 與 \([m+1,r]\) 分別排序好
再去算出橫跨 \(m\) 的答案
二維偏序問題 (逆序數對)
\((1,2)\)
\((3,1)\)
\((4,5)\)
\((2,4)\)
\((5,2)\)
\((7,3)\)
\((6,5)\)
\((8,4)\)
首先,假設我們要找這八個點的答案
二維偏序問題 (逆序數對)
\((1,2)\)
\((3,1)\)
\((4,5)\)
\((2,4)\)
\((5,2)\)
\((7,3)\)
\((6,5)\)
\((8,4)\)
第一步、將點依照 \(a_i\) 的大小進行排序
二維偏序問題 (逆序數對)
\((1,2)\)
\((4,5)\)
\((5,2)\)
\((7,3)\)
\((8,4)\)
第一步、將點依照 \(a_i\) 的大小進行排序
\((2,4)\)
\((3,1)\)
\((6,5)\)
二維偏序問題 (逆序數對)
\((1,2)\)
\((4,5)\)
\((5,2)\)
\((7,3)\)
\((8,4)\)
\((2,4)\)
\((3,1)\)
\((6,5)\)
第二步、分治
先做完 \([l,mid]\) 和 \([mid+1,r]\)的答案,再合併
二維偏序問題 (逆序數對)
\((1,2)\)
\((4,5)\)
\((5,2)\)
\((7,3)\)
\((8,4)\)
\((2,4)\)
\((3,1)\)
\((6,5)\)
第二步、分治
先做完 \([l,mid]\) 和 \([mid+1,r]\)的答案,再合併
ans = \(0\)
二維偏序問題 (逆序數對)
\((1,2)\)
\((4,5)\)
\((5,2)\)
\((7,3)\)
\((8,4)\)
\((2,4)\)
\((3,1)\)
\((6,5)\)
第二步、分治
先做完 \([l,mid]\) 和 \([mid+1,r]\)的答案,再合併
ans = \(1\)
二維偏序問題 (逆序數對)
\((1,2)\)
\((4,5)\)
\((5,2)\)
\((7,3)\)
\((8,4)\)
\((2,4)\)
\((3,1)\)
\((6,5)\)
第二步、分治
先做完 \([l,mid]\) 和 \([mid+1,r]\)的答案,再合併
ans = \(2\)
二維偏序問題 (逆序數對)
\((1,2)\)
\((4,5)\)
\((5,2)\)
\((7,3)\)
\((8,4)\)
\((2,4)\)
\((3,1)\)
\((6,5)\)
第二步、分治
先做完 \([l,mid]\) 和 \([mid+1,r]\)的答案,再合併
ans = \(3\)
二維偏序問題 (逆序數對)
\((1,2)\)
\((4,5)\)
\((5,2)\)
\((7,3)\)
\((8,4)\)
\((2,4)\)
\((3,1)\)
\((6,5)\)
第二步、分治
先做完 \([l,mid]\) 和 \([mid+1,r]\)的答案,再合併
ans = \(4\)
二維偏序問題 (逆序數對)
\((1,2)\)
\((4,5)\)
\((5,2)\)
\((7,3)\)
\((8,4)\)
\((2,4)\)
\((3,1)\)
\((6,5)\)
第二步、分治
先做完 \([l,mid]\) 和 \([mid+1,r]\)的答案,再合併
ans = \(4\)
二維偏序問題 (逆序數對)
\((1,2)\)
\((4,5)\)
\((5,2)\)
\((7,3)\)
\((8,4)\)
\((2,4)\)
\((3,1)\)
\((6,5)\)
第二步、分治
先做完 \([l,mid]\) 和 \([mid+1,r]\)的答案,再合併
ans = \(4\)
二維偏序問題 (逆序數對)
\((1,2)\)
\((4,5)\)
\((5,2)\)
\((7,3)\)
\((8,4)\)
\((2,4)\)
\((3,1)\)
\((6,5)\)
第二步、分治
先做完 \([l,mid]\) 和 \([mid+1,r]\)的答案,再合併
ans = \(5\)
二維偏序問題 (逆序數對)
\((1,2)\)
\((4,5)\)
\((5,2)\)
\((7,3)\)
\((8,4)\)
\((2,4)\)
\((3,1)\)
\((6,5)\)
第二步、分治
先做完 \([l,mid]\) 和 \([mid+1,r]\)的答案,再合併
ans = \(6\)
二維偏序問題 (逆序數對)
\((1,2)\)
\((4,5)\)
\((5,2)\)
\((7,3)\)
\((8,4)\)
\((2,4)\)
\((3,1)\)
\((6,5)\)
第二步、分治
先做完 \([l,mid]\) 和 \([mid+1,r]\)的答案,再合併
ans = \(6\)
二維偏序問題 (逆序數對)
\((1,2)\)
\((4,5)\)
\((5,2)\)
\((7,3)\)
\((8,4)\)
\((2,4)\)
\((3,1)\)
\((6,5)\)
第二步、分治
先做完 \([l,mid]\) 和 \([mid+1,r]\)的答案,再合併
ans = \(8\)
二維偏序問題 (逆序數對)
\((1,2)\)
\((4,5)\)
\((5,2)\)
\((7,3)\)
\((8,4)\)
\((2,4)\)
\((3,1)\)
\((6,5)\)
第二步、分治
先做完 \([l,mid]\) 和 \([mid+1,r]\)的答案,再合併
ans = \(8\)
二維偏序問題 (逆序數對)
\((1,2)\)
\((4,5)\)
\((5,2)\)
\((7,3)\)
\((8,4)\)
\((2,4)\)
\((3,1)\)
\((6,5)\)
第二步、分治
先做完 \([l,mid]\) 和 \([mid+1,r]\)的答案,再合併
ans = \(8\)
二維偏序問題 (逆序數對)
\((1,2)\)
\((4,5)\)
\((5,2)\)
\((7,3)\)
\((8,4)\)
\((2,4)\)
\((3,1)\)
\((6,5)\)
第二步、分治
先做完 \([l,mid]\) 和 \([mid+1,r]\)的答案,再合併
ans = \(8\)
二維偏序問題 (逆序數對)
\((1,2)\)
\((4,5)\)
\((5,2)\)
\((7,3)\)
\((8,4)\)
\((2,4)\)
\((3,1)\)
\((6,5)\)
第二步、分治
先做完 \([l,mid]\) 和 \([mid+1,r]\)的答案,再合併
ans = \(12\)
二維偏序問題 (逆序數對)
\((1,2)\)
\((4,5)\)
\((5,2)\)
\((7,3)\)
\((8,4)\)
\((2,4)\)
\((3,1)\)
\((6,5)\)
第二步、分治
先做完 \([l,mid]\) 和 \([mid+1,r]\)的答案,再合併
ans = \(12\)
二維偏序問題 (逆序數對)
\((1,2)\)
\((4,5)\)
\((5,2)\)
\((7,3)\)
\((8,4)\)
\((2,4)\)
\((3,1)\)
\((6,5)\)
第二步、分治
先做完 \([l,mid]\) 和 \([mid+1,r]\)的答案,再合併
ans = \(15\)
二維偏序問題 (逆序數對)
\((1,2)\)
\((4,5)\)
\((5,2)\)
\((7,3)\)
\((8,4)\)
\((2,4)\)
\((3,1)\)
\((6,5)\)
第二步、分治
先做完 \([l,mid]\) 和 \([mid+1,r]\)的答案,再合併
ans = \(15\)
二維偏序問題 (逆序數對)
\((1,2)\)
\((4,5)\)
\((5,2)\)
\((7,3)\)
\((8,4)\)
\((2,4)\)
\((3,1)\)
\((6,5)\)
第二步、分治
先做完 \([l,mid]\) 和 \([mid+1,r]\)的答案,再合併
ans = \(16\)
二維偏序問題 (逆序數對)
\((1,2)\)
\((4,5)\)
\((5,2)\)
\((7,3)\)
\((8,4)\)
\((2,4)\)
\((3,1)\)
\((6,5)\)
第二步、分治
先做完 \([l,mid]\) 和 \([mid+1,r]\)的答案,再合併
ans = \(16\)
三維偏序問題
給你兩個陣列 \(A,B\),問總共有幾對 \(i,j\) 滿足
\((a_i < a_j )\land (b_i < b_j) \land (c_i < c_j)\)
這個問題好像就沒那麼好解決了?
二維 BIT!
不過我們還是能用 CDQ 分治解決!
三維偏序問題
1. 我們可以藉由排序 \(a_i\) 減少一個維度,使得問題變為二維偏序
2. 接著,我們考慮對原問題進行分治
先處理 \([l,mid], \ [mid+1,r]\) 的答案
思考如何計算 \([l,mid]\) 對 \([mid+1,r]\) 造成的影響
最後再將陣列用 merge sort 以 \(b_i\) 排好
3. 我們可以搭配 BIT 去計算有幾對的 \(c_i < c_j\)
三維偏序問題
離線演算法
By sam571128
離線演算法
- 302



