Enumeration & Searching
UMD CP Club Summer CP Week 2
How to search?
Let's look at a simple problem
A simple problem
You are given an array of length \(n\), and the score of a subarray \(b_1, b_2, \cdots, b_k\) is defined as following
s_{lr} = b_1 + 2b_2 + 3b_3 + \cdots + kb_k
Find the maximum \(s_{lr}\) over all subarray
* A subarray is a continuous subsequence of the original array
Approach 1
Fix \(l\) and \(r\), then go over all \(l \le i \le r\) to sum up score
Approach 1
Fix \(l\) and \(r\), then go over all \(l \le i \le r\) to sum up score
int ans = arr[1];
for (int l = 1; l <= n; l++) {
for(int r = 1; r <= n; r++){
int sum = 0;
for(int i = l; i <= r; i++){
sum += arr[i] * (i - l + 1);
}
ans = max(ans, sum)
}
}O(n^3)
Approach 2
Fix \(l\), then move \(r\) to find the answer
Approach 2
Fix \(l\), then move \(r\) to find the answer
int ans = arr[l];
for (int l = 1; l <= n; l++) {
int sum = 0;
for(int r = 1; r <= n; r++){
sum += arr[r] * (r - l + 1);
ans = max(ans, sum);
}
}O(n^2)
Approach 3
How can we make this even faster?
Approach 3
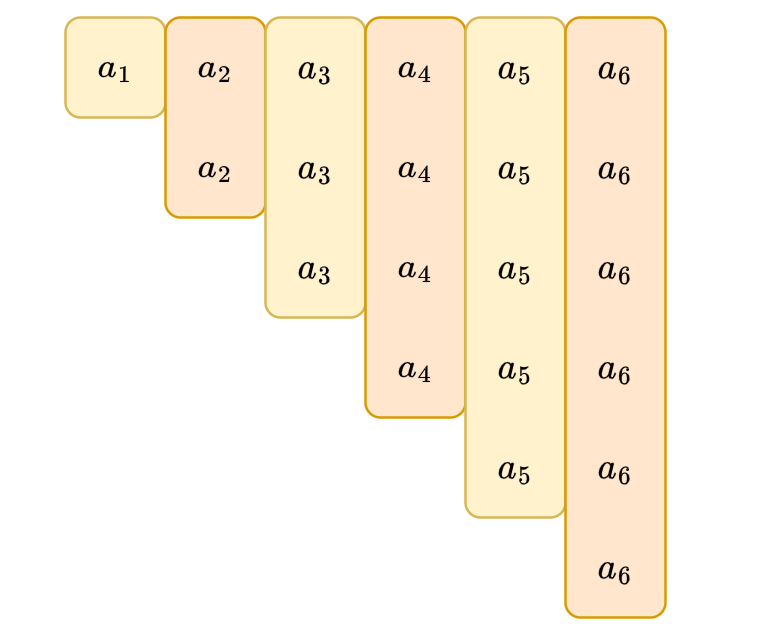
Approach 3
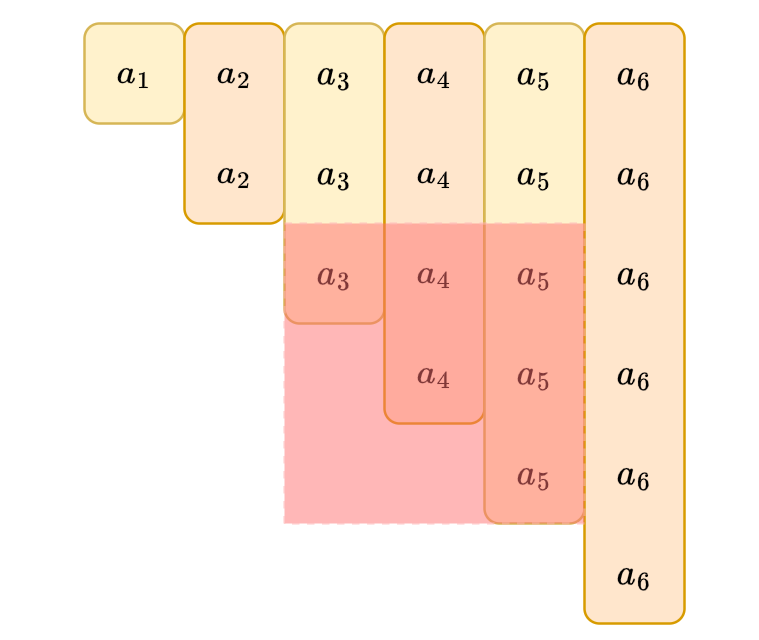
Approach 3
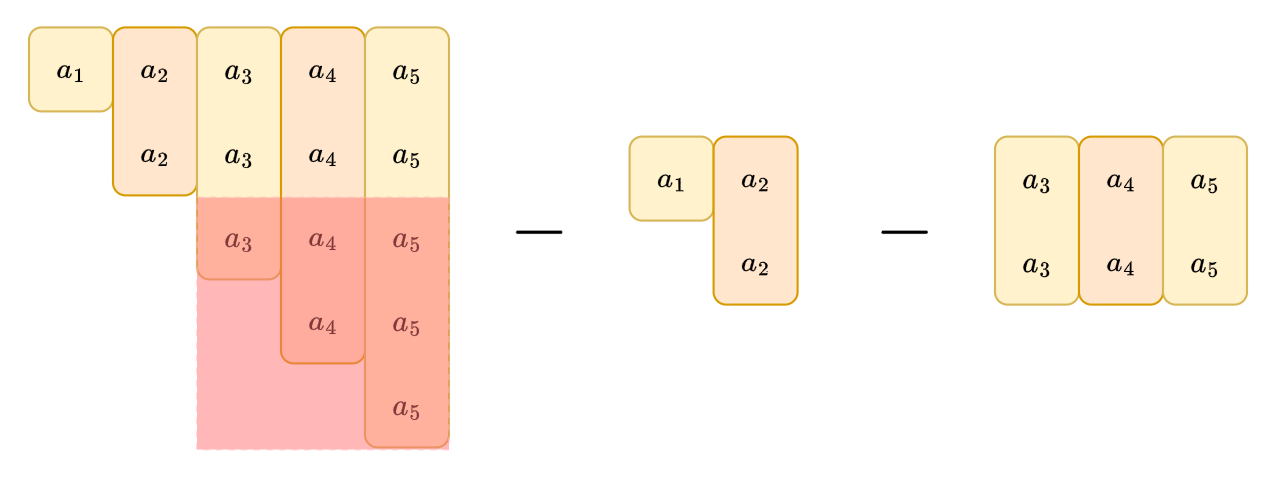
This is the brief idea
The rest will be an exercise for you
Make this \(O(n)\) or \(O(n \log n)\)
However, not everytime you can solve a problem
just by using a loop like that
Let's look at another problem
Travelling Salesman Problem
Travelling Salesman Problem
Travelling Salesman Problem
Travelling Salesman Problem
Minimize the distance!
Travelling Salesman Problem
There are \(n\) points on the plane
Find the minimum Hamiltonian Circuit\(^*\)
*Cycle that goes through all points
Travelling Salesman Problem
Go through all possible orders
Travelling Salesman Problem
Go through all possible orders
\(1 \to 2 \to 3 \to 4 \to 5 \to 1\)
\(1 \to 3 \to 2 \to 5 \to 4 \to 1\)
\(\vdots\)
How to do this?
Travelling Salesman Problem
C++ next_permutation!
Travelling Salesman Problem
C++ next_permutation!
vector<int> v(n);
iota(v.begin(), v.end(), 1); //v = {1,...,n}
do{
//v will go through all possible permutations
}while(next_permutation(v.begin(), v.end()));Travelling Salesman Problem
vector<int> v(n);
iota(v.begin(), v.end(), 1); //v = {1,...,n}
int ans = 1e9; //some large number
do{
int sum = 0;
for (int i = 0; i < n; i++) {
sum += distance(p[v[i]], p[v[(i+1)%n]]);
}
ans = max(ans, sum);
}while(next_permutation(v.begin(), v.end()));O(n!)
Travelling Salesman Problem
We have solved this problem
by enumerating through all permutations!
Knapsack Problem
You have a knapsack with weight capacity \(W\)
There are \(n\) items, each with \(w_i\) weight and value \(v_i\)
What is the maximum sum of values you can bring?
- \(1 \le n \le 20\)
- \(1 \le w_i, v_i \le 10^9\)
Knapsack Problem
How to search over all possibilities?
Knapsack Problem
Or in other words, search over all subsets!
Knapsack Problem
We can do this with recursion
Knapsack Problem
int ans = 0;
void search(int idx = 0, int sum = 0, int cap = 0) {
if (cap > W) return;
if (idx == n) {
ans = max(ans, sum);
return;
}
search(idx + 1, sum + v[i], cap + w[i]); //take ith item
search(idx + 1, sum, cap); //don't take ith item
}O(2^n)
Knapsack Problem
However, Competitive Programmer usually hate recursions!
(large constants)
Knapsack Problem
Since \(n \le 20\), we can do this
01010100101...
represents whether we take \(i\)-th item or not
Knapsack Problem
\(001, \ 010, \ 011, \ 100, \ 101, \ 110, \ 111\)
This is \(1 \sim 8\) in binary!
Knapsack Problem
For people who don't know binary operations
a | b means \(a \text{ or } b\)
a & b means \(a \text{ and } b\)
a ^ b means \(a \text{ xor } b\)
a << b means \(a\) left shifted by \(b\) bits \((a \times 2^b)\)
a >> b means \(a\) right shifted by \(b\) bits \((\lfloor a / 2^b \rfloor)\)
Knapsack Problem
int ans = 0;
for (int mask = 0; mask < (1 << n); i++) {
int sum = 0, cap = 0;
for (int i = 0; i < n; i++) {
if (mask & (1 << i)) {
sum += v[i];
cap += w[i];
}
if(cap <= W) ans = max(ans, sum);
}
}O(n2^n)
- Searching over subarrays => for loops
- Searching over permutations => next_permutation
- Searching over all subsets => recursion / bit operations
Three ways of searching through states
What if you want to generate permutations with \(k\) elements Or generate subsets taking \(k\) elements
Permutation with \(k\) elements
vector<int> v(k, 1);
v.resize(n, 0);
do{
vector<int> idx;
for(int i = 0; i < n; i++){
if(v[i]) idx.push_back(i);
}
}while(next_permutation(v.begin(), v.end()));Subsets with \(k\) elements
for (int mask = 0; mask < (1 << n); mask++) {
if(__builtin_popcount(mask) == k){
//Do something
}
}Backtracking (DFS)
Sudoku
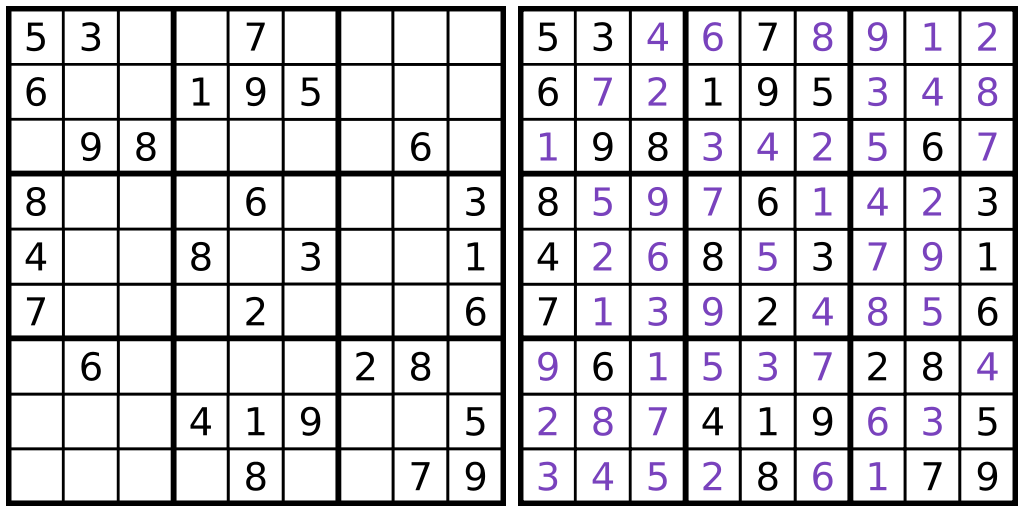
Sudoku
If you calculate all possibilities
There can be up to \(O(9^{81})\) states!
Do you really need to search that many?
From sudoku, we learned that
Under specific rules, we can do it fast!
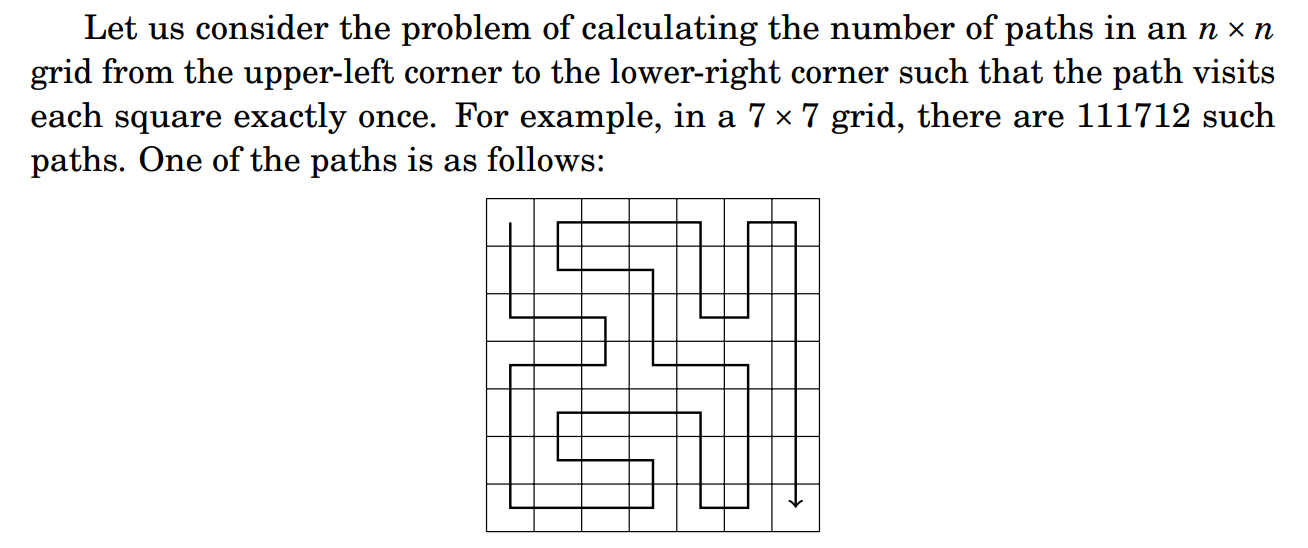
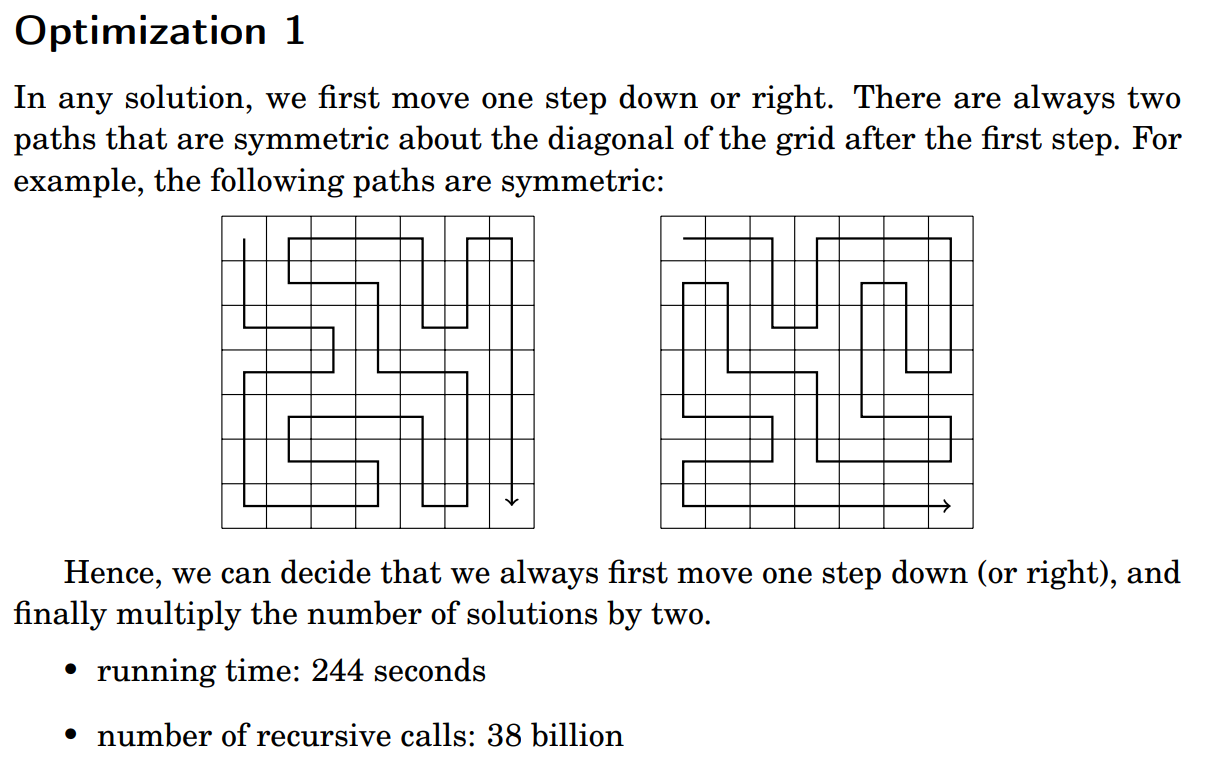
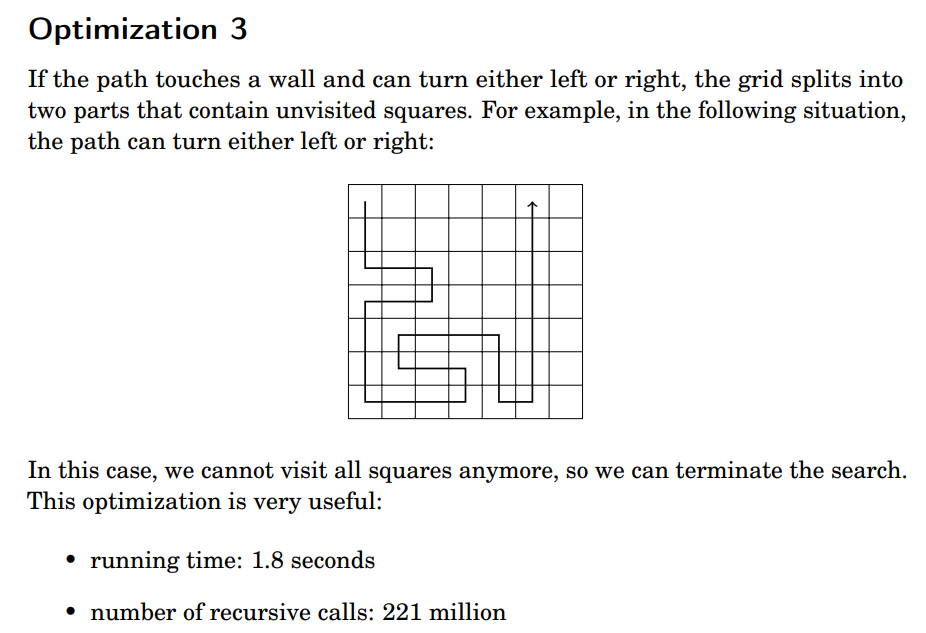
This is called Pruning
For backtracking, there is not much I can teach
You just have to practice
Two Pointers
Let's look at a problem
CSES - Subarray Distinct Values
You are given an array of length \(n\), find the number of subarrays such that it has at most \(k\) distinct values
It is easy! Why don't we just search for all the subarrays like the problem we talked about?
You are given an array of length \(n\), find the number of subarrays such that it has at most \(k\) distinct values
You are given an array of length \(n\), find the number of subarrays such that it has at most \(k\) distinct values
n \le 10^6
r
l
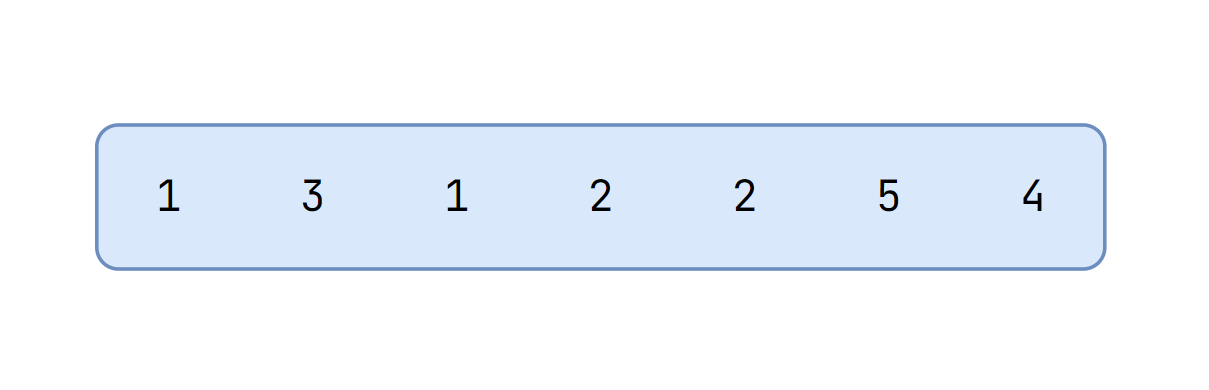
Suppose we fix l and move r
r
l
\text{counter} = 1
r
l
\text{counter} = 2
r
l
\text{counter} = 2
r
l
\text{counter} = 3
r
l
\text{counter} = 3
r
l
\text{counter} = 4
When we fix l and only moves r to right
The distinct value count can only increase by 1 or stay the same
r
l
Now, we fix r and move l to the right
r
l
Now, we fix r and move l to the right
r
l
\text{counter} = 3
r
l
\text{counter} = 3
r
l
\text{counter} = 2
r
l
\text{counter} = 1
When we fix r and only moves l to right
The distinct value count can only decrease by 1 or stay the same
If we can find the farthest \(r\) for each \(l\)
such that the subarray \([l,r]\) satisfies the condition
Then for all \(l \le i \le r\), \([l,i]\) must satisfy the condition
map<int,int> cnt;
int r = 0, num = 0, ans = 0;
for (int l = 1; l <= n; l++) {
while(r+1 <= n && (num + (cnt[arr[r+1]] == 0) <= k)) {
r++;
cnt[arr[r]]++;
num += (cnt[arr[r]] == 1);
}
ans += (r - l + 1);
cnt[arr[l]]--;
if(cnt[arr[l]] == 0) num--;
}O(n \log n)
We learned that two pointers can solve
Longest Subarray
Number of Subarrays
in \(O(n) \times O(k)\)
where \(k\) is the complexity to move one pointer
I recommend you to solve
Binary Search
Let's look at a famous problem!
There is a hidden number \(x\) from \(1\) to \(n\)
You can guess a number, and I will tell you if the number is greater, less than, or equal to \(x\)
What is the minimum number of guesses that you can always find the answer
< mid
> mid
Every time, we can cut the interval into half
Therefore, we can do this in \(\lceil \log n \rceil\) times
This is the idea of binary search!
int l = 1, r = n;
while (l < r) {
int mid = (l + r) / 2;
if (ask(mid) == "LESS"){
r = mid - 1;
} else if (ask(mid) == "GREATER") {
l = mid + 1;
} else {
ans = mid;
}
}O(\log n)
This idea is useful!
We can use this to make searching faster!
If you have a sorted array and you want to find if \(x\) exists in the array
Approach 1 - Linear Search
Start from the beginning, and go through all elements!
for (int i = 0; i < n; i++) {
if (arr[i] == x) {
cout << "FOUND!\n";
return 0;
}
}
cout << "NOT FOUND!\n";O(n)
Approach 2 - Binary Search
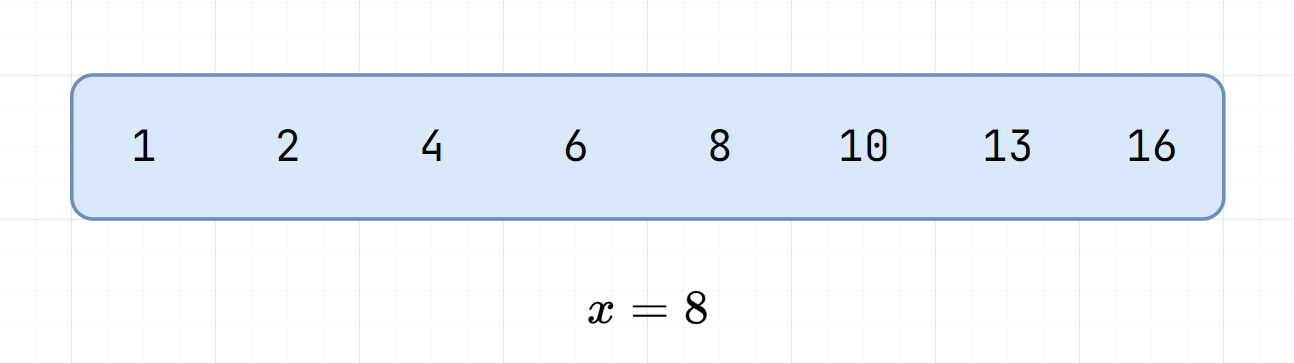
Approach 2 - Binary Search
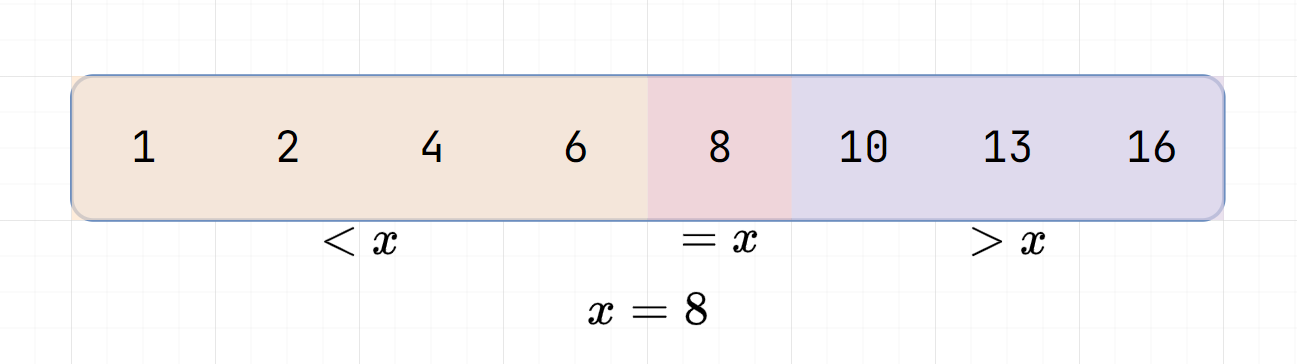
Isn't this the same as guessing numbers?
Approach 2 - Binary Search
int l = 1, r = n;
while (l < r) {
int mid = (l + r) / 2;
if (arr[mid] == x){
r = mid - 1;
} else if (arr[mid] == x) {
l = mid + 1;
} else {
cout << "FOUND x at " << mid << "\n";
}
}O(\log n)
What if you want to find first > x in the array?
Upper Bound
Now, there's only two parts \(< x\) and \(> x\)
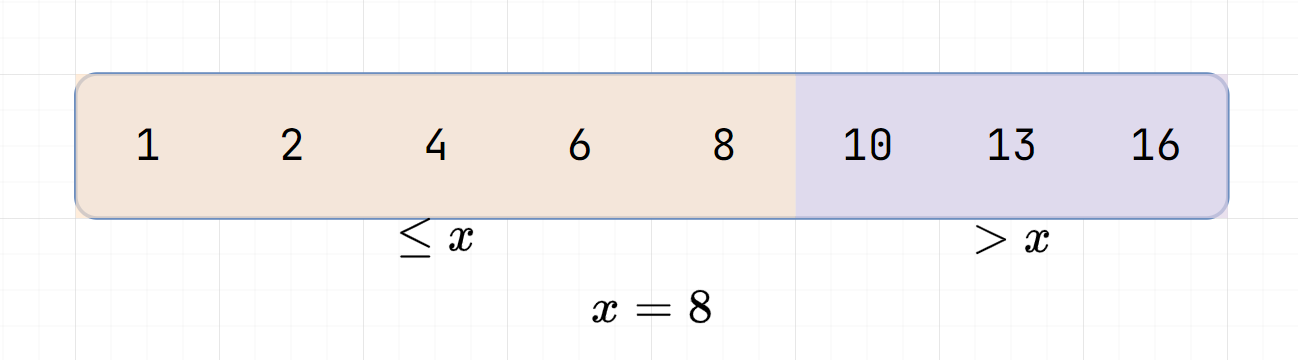
Upper Bound
mid
Since \(arr[4] = 6 \le x\),
the possible interval is \([5,8]\)
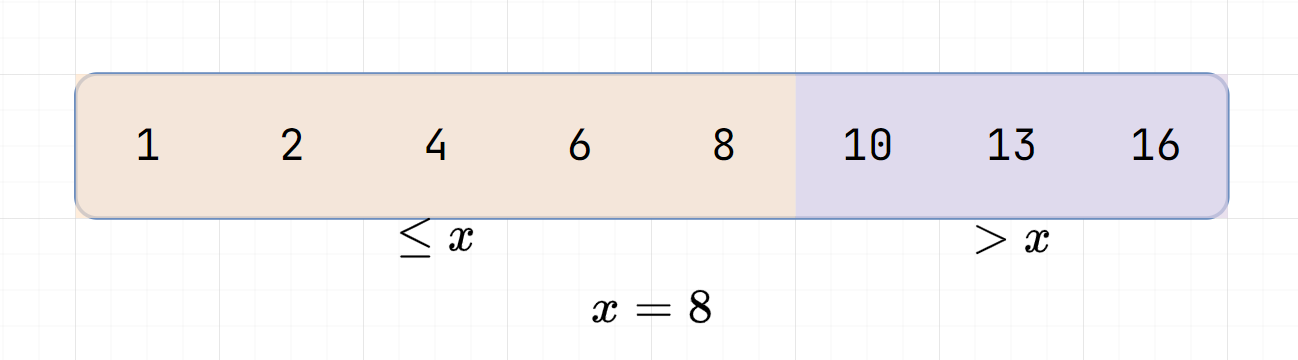
Upper Bound
mid
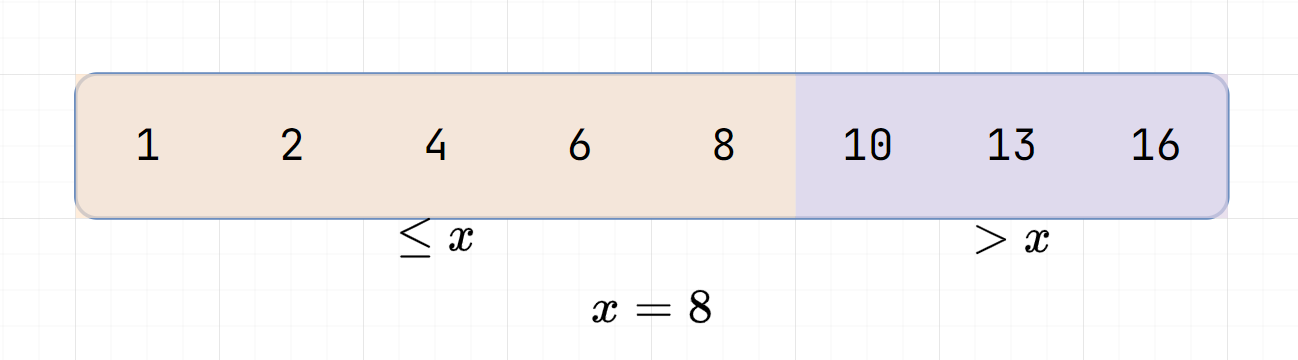
Since \(arr[7] = 13 > x\)
The possible interval is \([5,7]\)
It is not 7-1!
Upper Bound
int l = 1, r = n;
while (l < r) {
int mid = (l + r) / 2;
if (arr[mid] > x) r = mid;
else l = mid+1;
}
cout << r << "\n";Since we are finding first \(> x\)
We cannot exclude mid when \(> x\)
What if now you want to find the last element \(\le x\)
Upper Bound
Upper Bound
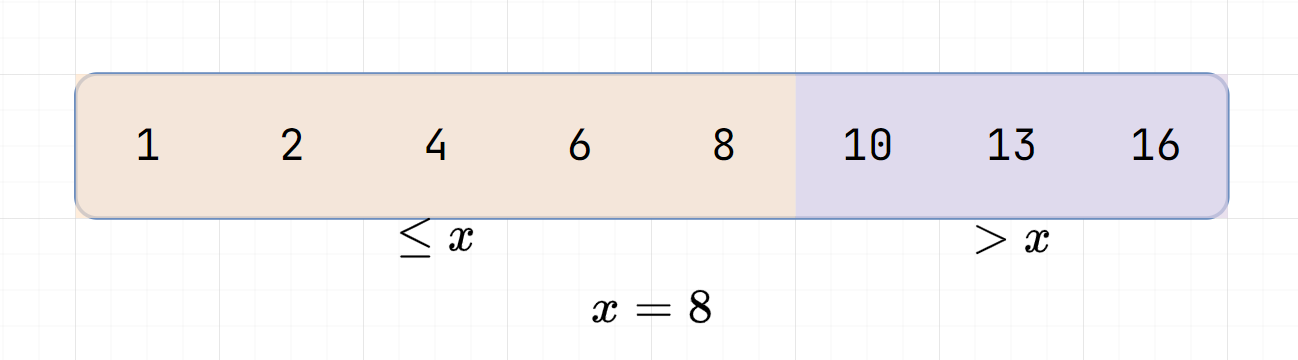
Upper Bound
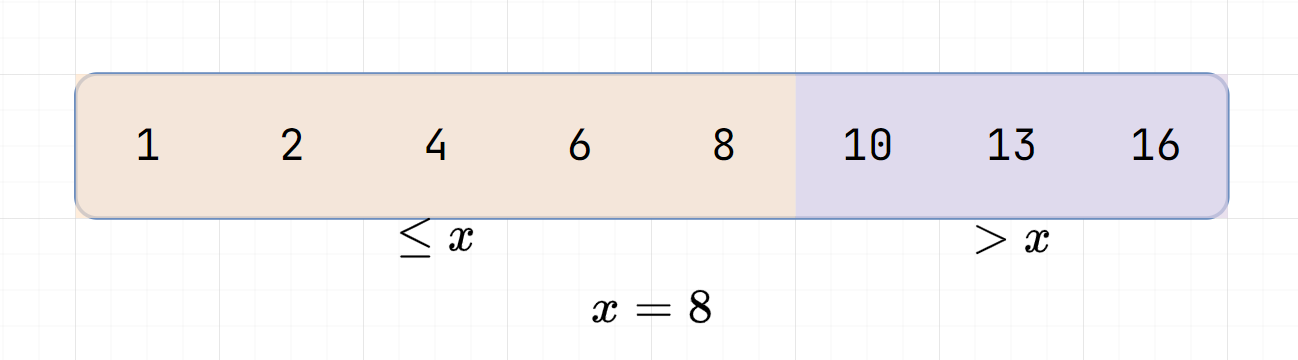
mid
You have to set interval to
\([4,8]\) instead of \([5,8]\)
Upper Bound
int l = 1, r = n;
while (l < r) {
int mid = (l + r) / 2;
if (arr[mid] <= x) l = mid;
else r = mid-1;
}
cout << r << "\n";Wait... Is this correct?
l = 1, r = 2, arr[l] \le x
Upper Bound
int l = 1, r = n;
while (l < r) {
int mid = (l + r + 1) / 2;
if (arr[mid] <= x) l = mid;
else r = mid-1;
}
cout << r << "\n";You have to make \(mid = (l+r+1)/2\)
C++ STL
Actually, both upper bound and lower bound
are implemented in C++ STL
Binary Search on Answer
Can we apply this idea for other problems?
A factory has \(n\) machines which can be used to make products. Your goal is to make a total of \(t\) products.
For each machine, you know the number of seconds it needs to make a single product. The machines can work simultaneously, and you can freely decide their schedule.
What is the shortest time needed to make \(t\) products?
The problem seems hard.
What if we change the problem?
Knowing the required time for each machine to generate a product. Find how many products the machines can generate in \(x\) time
int sum = 0;
for (int i = 0; i < n; i++) {
sum += x / a[i];
}This finds the answer!
But the original problem want to find the shortest time to generate \(t\) products
Now, we have this tool
bool check(int x) {
int sum = 0;
for (int i = 0; i < n; i++) {
sum += x / a[i];
}
return sum >= t;
}
We want to find the first element > 0
in a sorted 0-1 sequence!
long long l = 0, r = 1e18;
while (l < r) {
long long mid = (l+r) / 2;
if(check(mid)) r = mid;
else l = mid+1;
}
cout << r << "\n";We check in \(O(n)\)
and search in \(O(\log n)\)
Total: \(O(n \log n)\)
We usually call this
"Binary Search on Answers"
Maximum Length \(\Rightarrow\) Search for the rope length!
First thing for binary search!
Think about how to check for x
bool check(double x) {
int num = 0;
for (int i = 0; i < n; i++) {
num += floor(a[i] / x);
}
return num >= k;
}
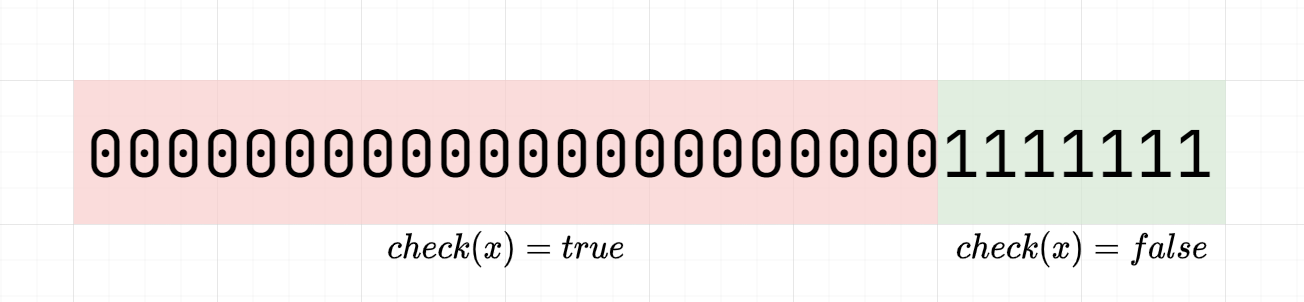
We want to find last element \(\le 0\)
in a sorted 0-1 sequence
Another difference is that
the answer might not be an integer
We want \(\epsilon \le 10^{-6}\)
If the interval size \(|r-l| \le \epsilon\)
the answer should be in the error bound
double l = 0, r = 1e7;
while (r - l >= 1e-6) {
double mid = (l + r) / 2;
if(check(mid)) l = mid;
else r = mid;
}
cout << l << "\n";This would work for float number binary search
O(\log (\frac{r-l}{\epsilon}) n)
double l = 0, r = 1e7;
for (int i = 0; i < 100; i++) {
double mid = (l + r) / 2;
if(check(mid)) l = mid;
else r = mid;
}
cout << l << "\n";This way, we can ignore the epsilon!
O(cn)
Also, since I didn't mention this last week
To output float numbers in C++
Also, since I didn't mention this last week
To output float numbers in C++
cout << fixed << setprecision(5);
cout << 2.0; //2.00000Common Error
int l = -1e9, r = 1e9;
while (l < r) {
int mid = (l + r) / 2;
if(check(mid)) r = mid;
else l = mid+1;
}When there is negative integer
\(\dfrac{l}{r}\) becomes ceiling!
Common Error
int l = -1e9, r = 1e9;
while (l < r) {
int mid = l + (r - l) / 2;
if(check(mid)) r = mid;
else l = mid+1;
}Change mid = l + (r - l) / 2
or l + (r - l + 1) / 2
Binary Search on Minimax
Think about this
If we can bound the sum, isn't it easy to count how many segments we need?
bool check(int x) {
int sum = 0, cnt = 1;
for (int i = 0; i < n; i++) {
if (sum + a[i] > x) {
cnt++;
sum = a[i];
} else {
sum += a[i];
}
}
return cnt <= k;
}Since divide into \(k\) segments
is actually same as divide into \(\le k\)
When you see \(\min\) and \(\max\)
it is usually solvable with binary search on answer!
Binary Search on Average
Let's take all subsets of size \(k\)!
Is there some way to make finding maximum easier?
What if we change the problem into
if there exists a subset such that the ratio is \(\ge x\)?
\frac{a_1 + a_2 + \cdots + a_k}{b_1 + b_2 + \cdots + b_k} \ge x
a_1 + a_2 + \cdots + a_k \ge x(b_1 + b_2 + \cdots + b_k)
(a_1-b_1x) + (a_2-b_2x) + \cdots + (a_k-b_kx) \ge 0
So, the idea becomes
let's assign each pair \((a_i, b_i)\)
the value \(c_i = (a_i - b_ix)\)
Now, you only need to check if you can take \(k\) elements from \(c_i\) such that the sum is \(\ge 0\)
bool check(double x) {
vector<double> c;
for (int i = 0; i < n; i++) {
c.push_back(a[i] - b[i] * x);
}
sort(c.begin(), c.end(), greater<>());
int sum = 0;
for (int i = 0; i < k; i++) {
sum += c[i];
}
return sum >= 0;
}Then, we solved this problem in
O(n \log^2 n)
If you can do average, can you do median?
Binary Search Kth Element
Let's do a simple problem
Kth Minimum Element in Array
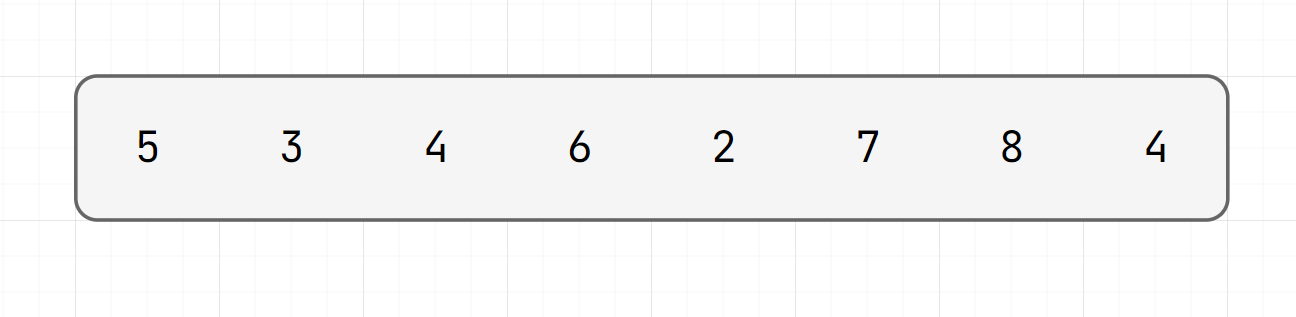
Try to find 4th smallest element without sorting the array
Kth Minimum Element in Array
Find the element of the rank is hard
What about finding the rank of an element?
Kth Minimum Element in Array
Suppose we want to know the rank of \(7\)
Kth Minimum Element in Array
Suppose we want to know the rank of \(7\)
We can count how many elements \(< 7\)
Kth Minimum Element in Array
We transformed the problem into
Finding the rank of \(x\)
bool check(int x) {
int cnt = 0;
for (int i = 0; i < n; i++) {
if(arr[i] < x) cnt++;
}
return cnt >= k;
}Kth element \(\equiv\) First element with rank \(\ge k\)
Ternary Search
You have a unimodal function
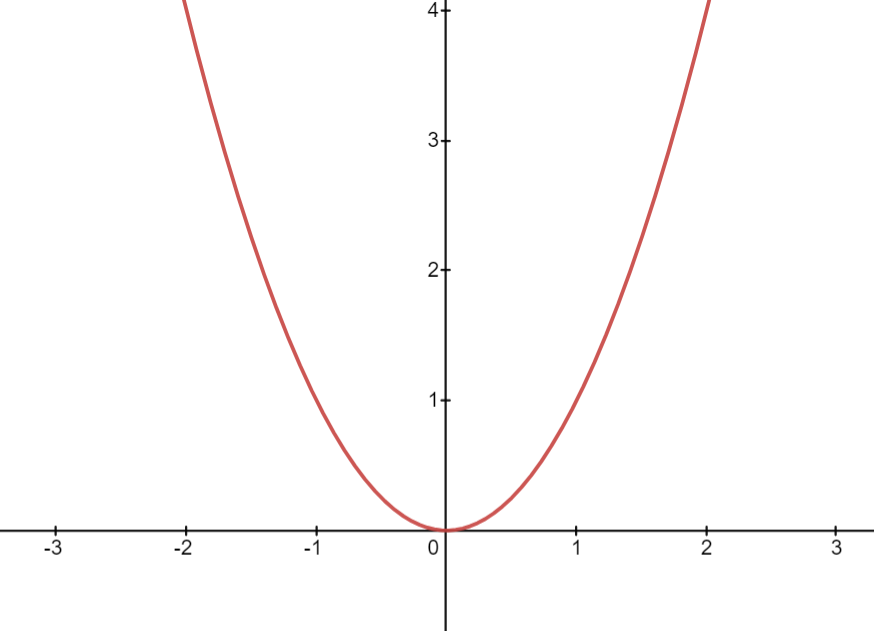
Find the minimum value of this function
How to find local minimum in a function?
Derivative
We want a way to search for the minimum
l
r
l
r
m_1
m_2
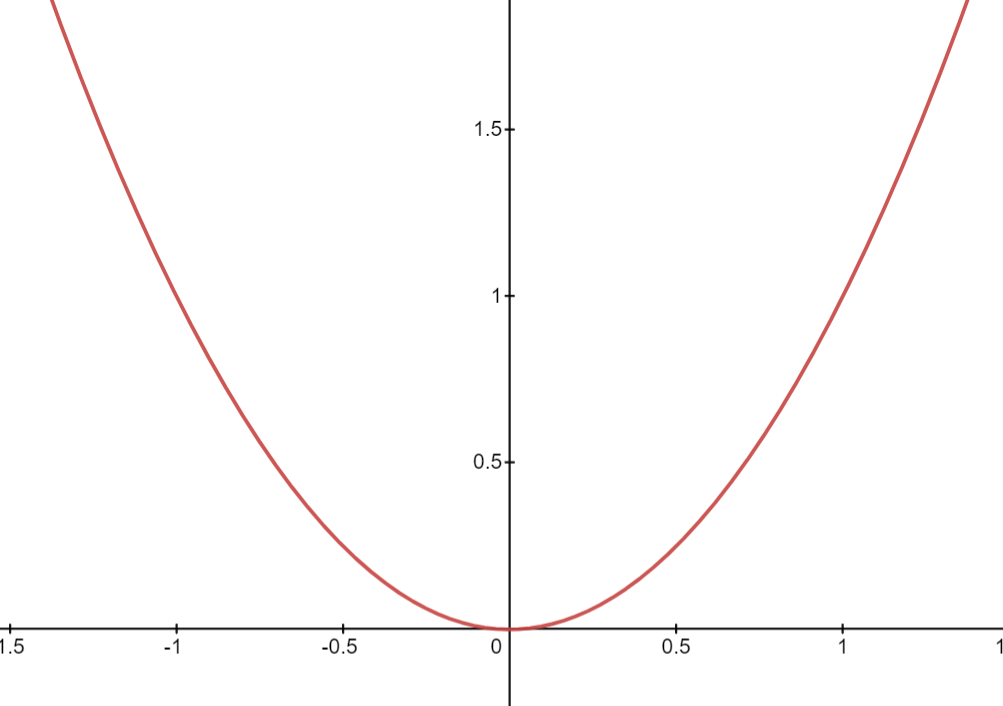
We have three cases (I will draw it on whiteboard)
If \(f(m_1) < f(m_2)\), then minimum is on the left of \(m_2\)
If \(f(m_1) > f(m_2)\), then minimum is on the right of \(m_1\)
If \(f(m_1) = f(m_2)\), then minimum is \(m_1\) or \(m_2\)
So we need to do this
If \(f(m_1) < f(m_2)\), set \(r := m_2\)
If \(f(m_1) \ge f(m_2)\), set \(l := m_1\)
double f(double x){
return x * x;
}
signed main(){
fastio
double l = -10, r = 10;
for(int i = 0; i < 100; i++){
double m1 = l + (r-l)/3;
double m2 = r - (r-l)/3;
if(f(m1) < f(m2)) r = m2;
else l = m1;
}
cout << fixed << setprecision(5) << l << " " << f(l) << "\n";
}T(n) = T(\frac{2}{3}n) + O(1) \\
\implies O(\log n)
If you want to do integer ternary search
int l = 0, r = 1e9+7;
while(l < r){
int mid = (l + r) / 2;
if(check(mid) < check(mid+1)) r = mid;
else l = mid+1;
}Compare \(f(mid)\) and \(f(mid + 1)\) is sufficient
Summary of Today's Content
- Searching over subarrays => for loops
- Searching over permutations => next_permutation
- Searching over all subsets => recursion / bit operations
- Searching for number of subarrays => two pointers
- Searching for longest subarray => two pointers
- Searching answer on sorted array => binary search
- Searching answer of \(\min(\max(...))\) => binary search
- Searching max/min average/median => binary search
- Searching max/min on concave function => ternary search
Strongly Recommend CF EDU
UMD Summer CP - Enumeration & Searching
By sam571128
