Exercise 1
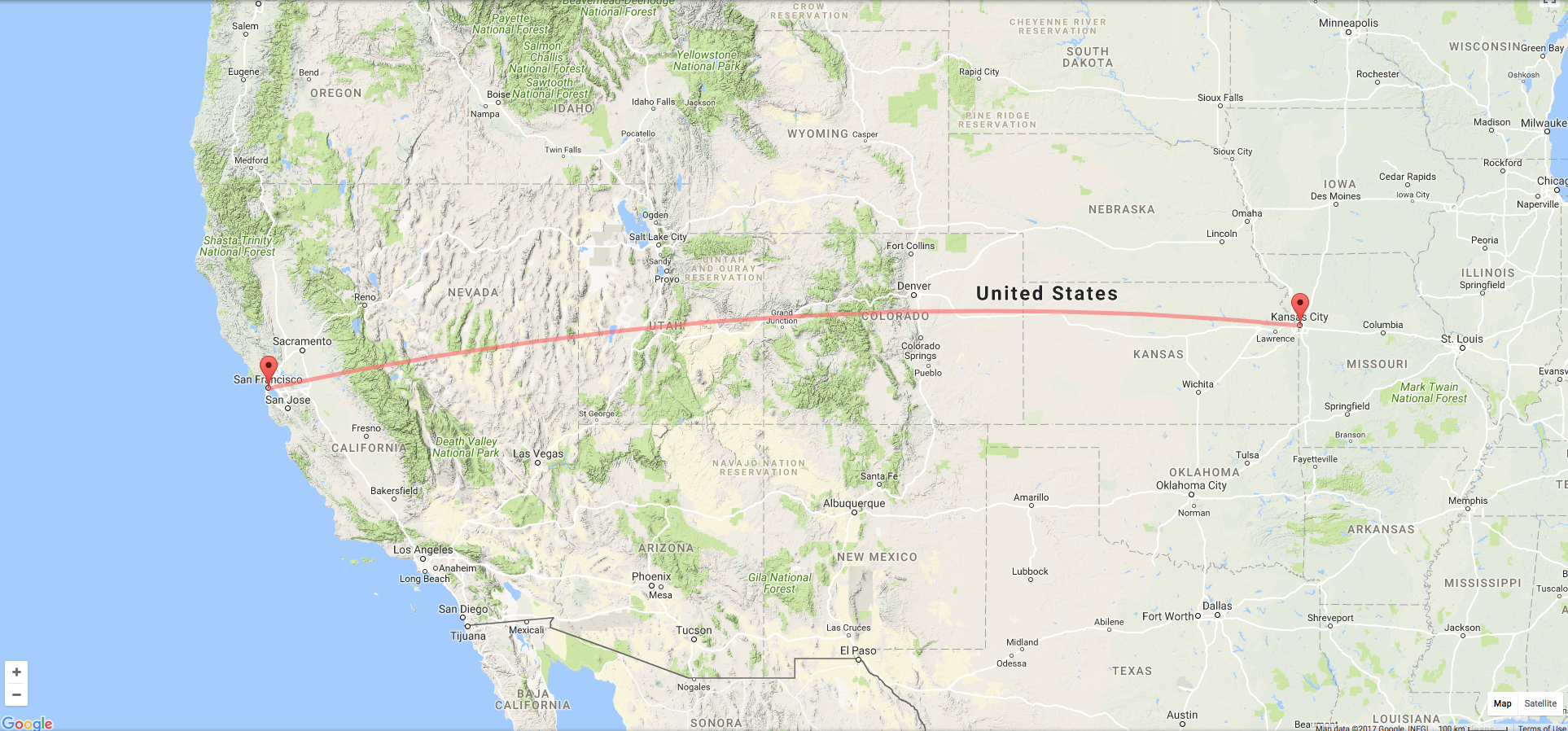
Call someone between 1000 and 3000 miles away at night and have them identify a star that is directly above them. You do the same. Note the stars, and then measure the angle of difference between your star and your friend's star.
Distance from SF to KC, about 1505 miles
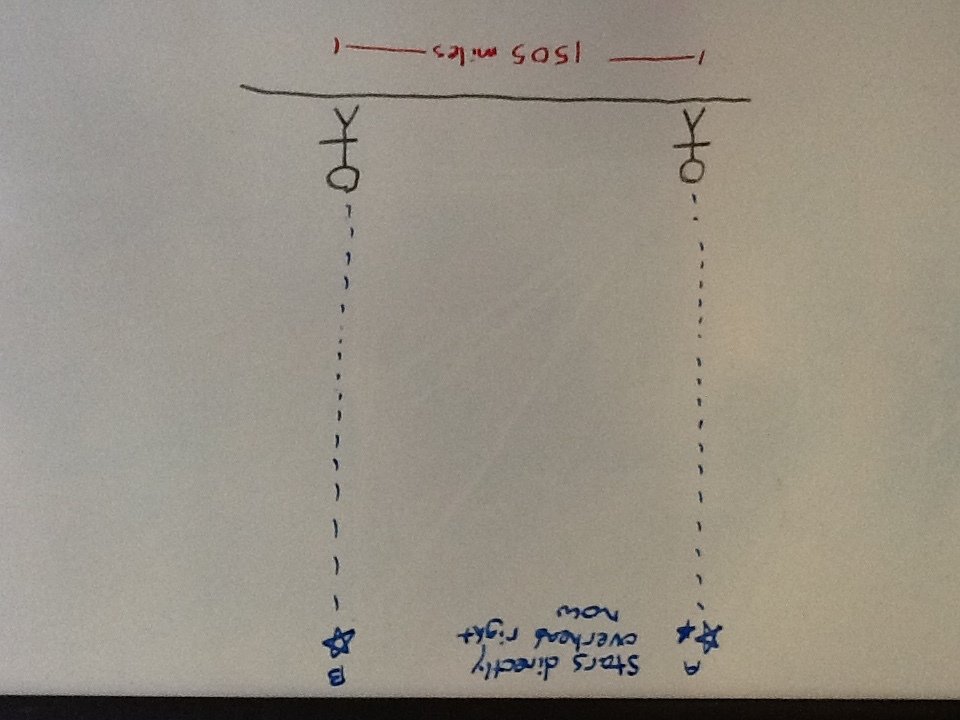
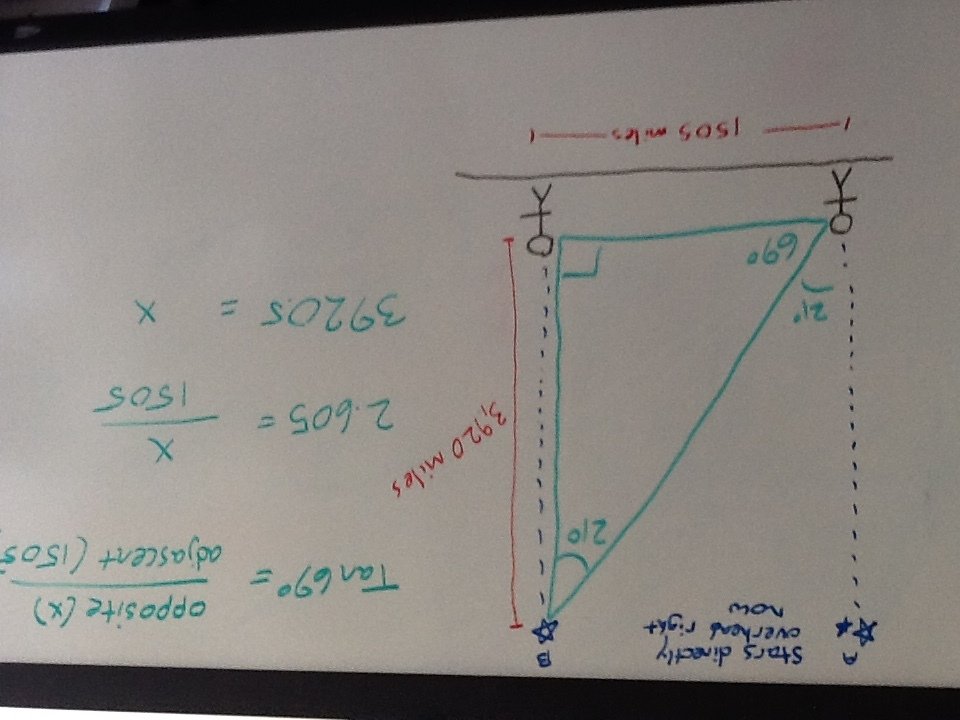
Let's assume the Earth is flat. A diagram of the two stars being directly overhead would look like this. Another way to think of it is like if two people were in different parts of the same room, they would look up seeing different parts of the same ceiling.
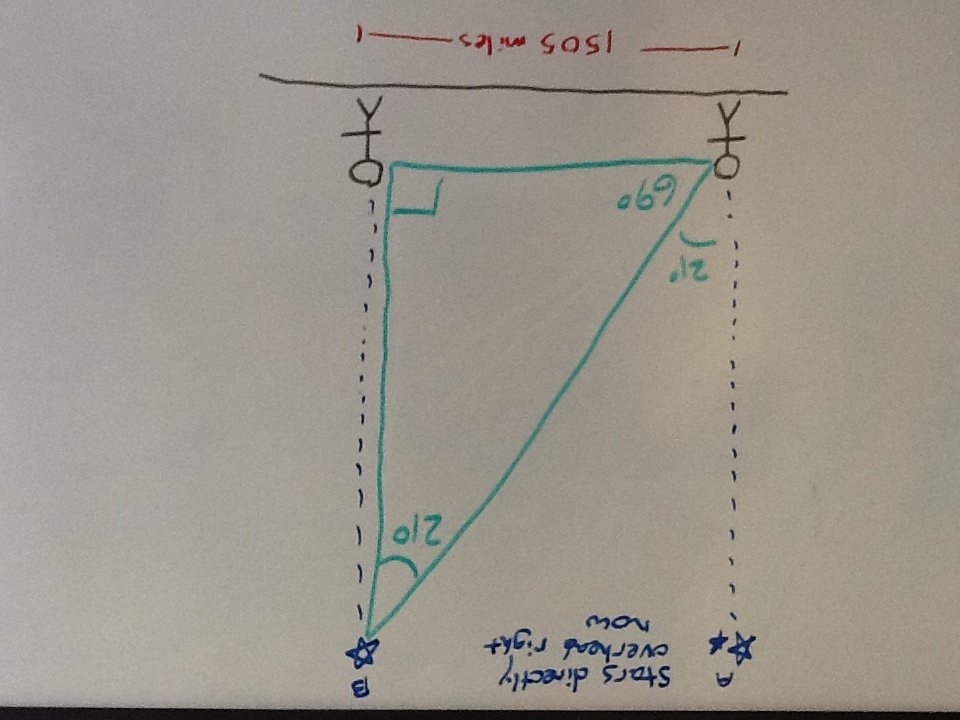
The angle of difference between the two stars is about 21 degrees. The goal now is to solve for the vertical side of the triangle. This will tell you how high up the star is.
A little trigonometry now...
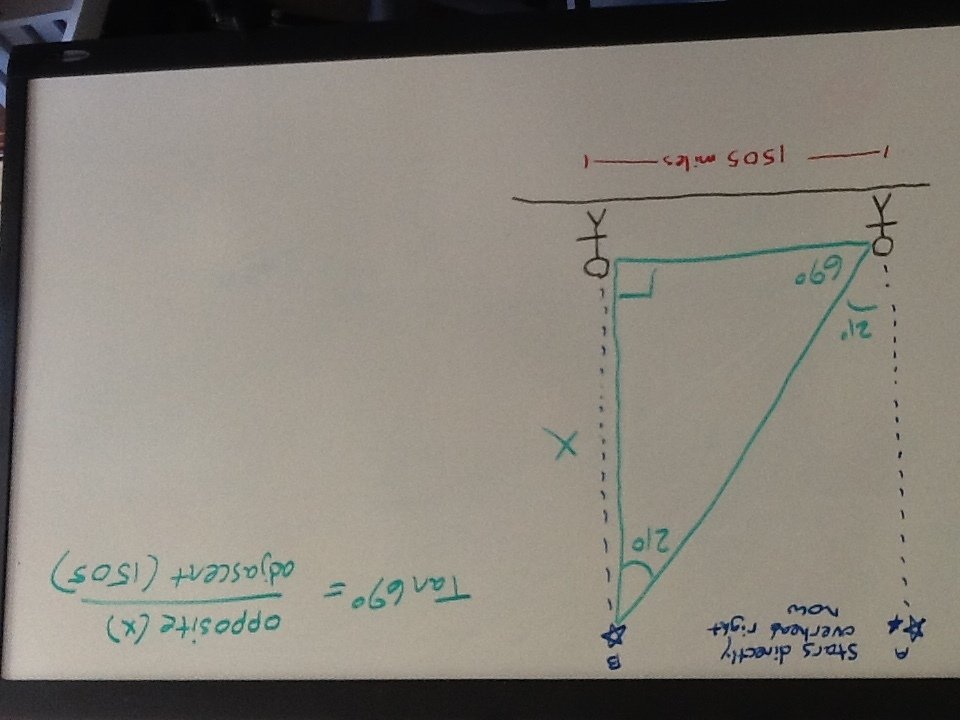
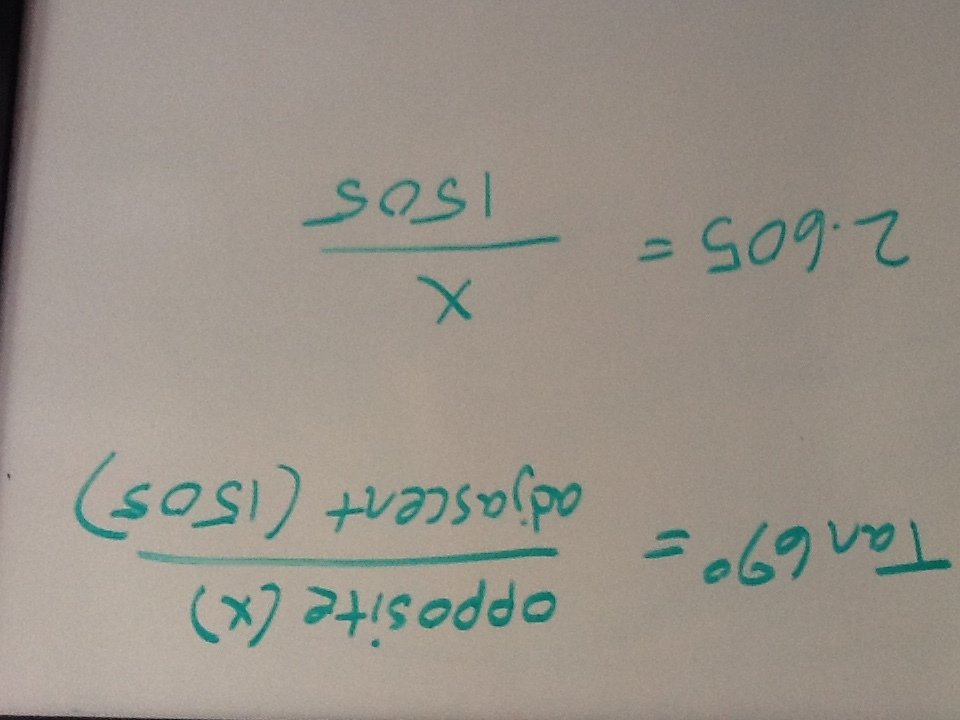
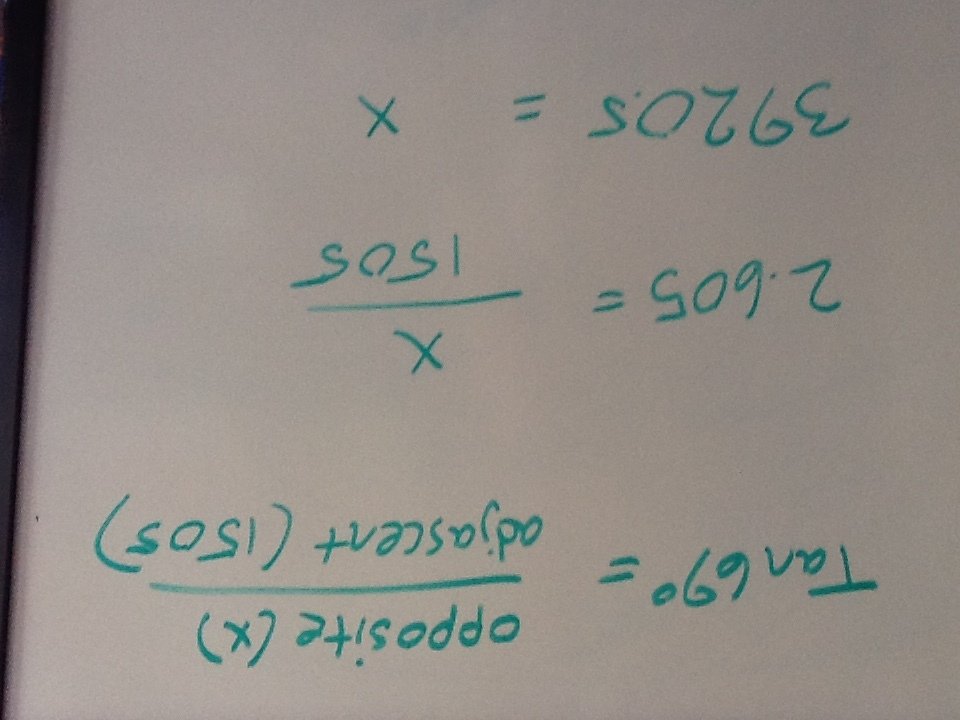
Now we have the calculated the distance to the star overhead: 3920 miles. Just out of curiosity, is this close to what other Flat Earth proponents have calculated?
Although it's hard to find consensus, some flat earth proponents have come up with similar figures...5458 km is 3391.4 miles.
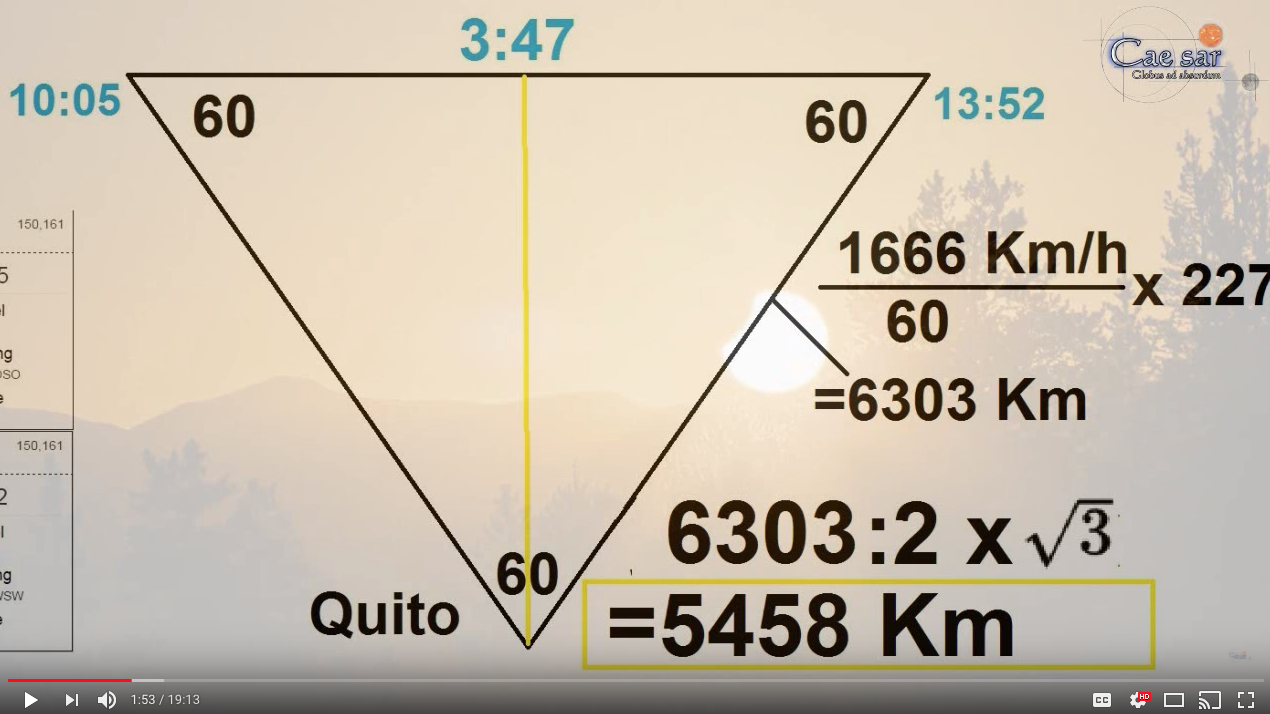
From "Sun Height" and star movement on Flat Earth"
This exercise can be repeated in many different places, and trying out various distances between observers. The outcome should be roughly the same. The apparent distance to the stars directly overhead should be around 3900 miles.
Hypothesis
If observations support this, then the surface of the celestial dome is roughly 3900 miles directly over all points of Earth's surface.
Let's try to figure out how far away the star is for the distant observer, rather than the one underneath. We already know that a star directly overhead is 3,900 miles away (repeat exercise 1 if necessary). So let's measure the distance to the star from someone way off to the side, say 6,000 miles.
Exercise 2
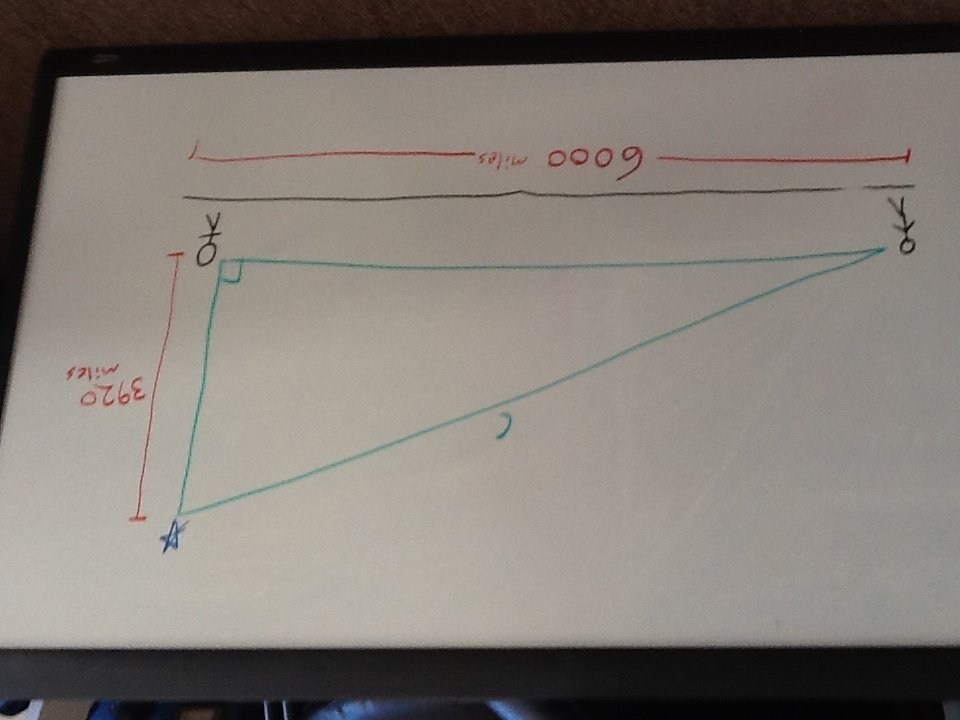
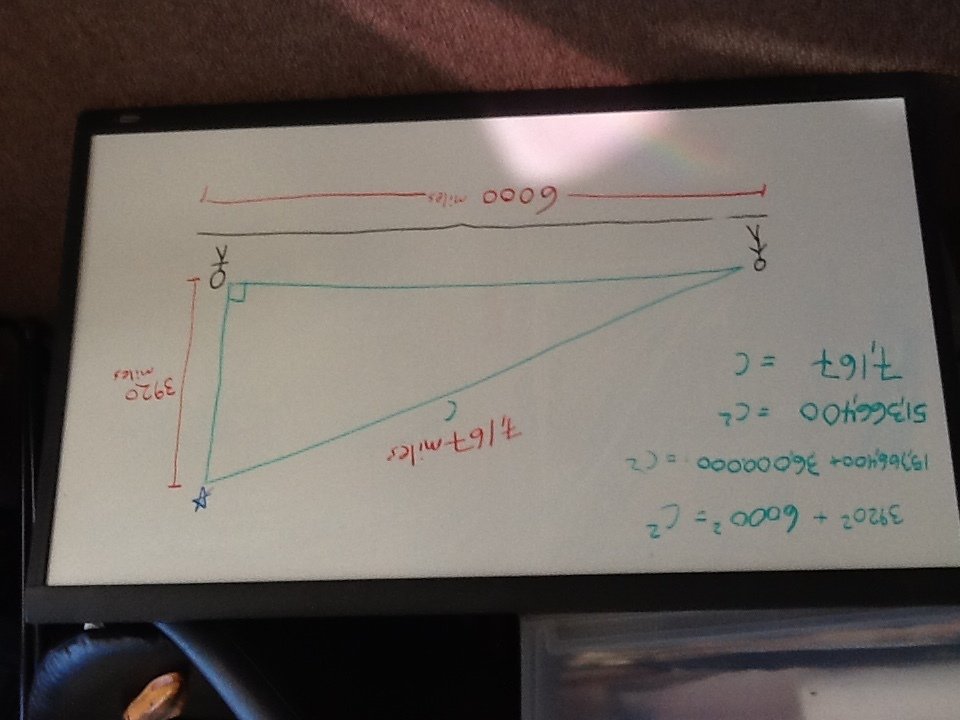
Solve for the hypotenuse...

The star is about 7,000 miles from the distant observer. That means it's almost twice as far away as it was when it was directly overhead...
An object is about 7,000 miles away from you, and 3900 miles away from someone else at the same exact time. Therefore, the object should appear twice as big to the person standing directly under it. If it's hard to imagine stars being bigger when they're closer, consider constellations instead. A constellation that's two times closer should appear bigger.
Or, another good object for these observations is the Moon. The moon can also be used for Exercise 1, although it might be more difficult for one of the observers to get directly under it.
Hypothesis 2
Celestial objects directly overhead are closer. Therefore they should appear bigger. But what does it mean if the apparent size doesn't change? The objects may be farther away than we originally calculated...
Let's say the stars are a million miles away. That would allow for virtually no change in apparent distance, no matter where a constellation was in the sky. It could be right overhead, or just at the horizon. The apparent size would be the same, and be consistent as it moved across the sky.
But there's a problem now. If this were the case then the same star(s) would appear directly overhead for both observers on a flat earth. If the observers stand a few thousand miles apart, and look up at a star a million miles overhead at the same time, it will appear directly overhead of both of them. You can also imagine two people standing one hundred feet apart in a room ten miles tall.
Discussion
So, two different observers a few thousand miles apart see different stars overhead. This is an observation that anyone can do. Why should this be so? And why don't the objects appear closer or farther away as they travel across the sky?
Furthermore, the Moon is arguably closer than the stars, as it moves in front of them. It's also closer than the sun, which it eclipses.
So whatever number we come up with as a distance to the stars overhead, the moon should be even closer (even if only a little.)
Speaking of the moon, is it a 3-D ball, or is it a disc? Let's say it's a ball. If two people are 6,000 miles apart, and they both look at the moon that's roughly 3,500 miles up in the air, would one of them be able to see a little more of one side of the moon? Another way to think about it is if two people are standing on opposite sides of the same dance floor, shouldn't they see different parts of the same disco ball?
Now let's say it's a flat disc. That would allow both observers to see the same side of the flat disc at all times, no matter where they stand. But then shouldn't it get foreshortened as it moves across the sky? If a flat disc looks round when it's directly overhead, shouldn't it look more flattened when viewed from off to one side?
More Discussion
deck
By Scott Calhoun
deck
- 282



